轨道点的上同调环

邓沙丽， 邓 绿， 杨海波

（1. 南昌航空大学 数学与信息科学学院，南昌 330063； 2. 赣东学院，江西 抚州 344000）

引 言

同调论在代数拓扑的研究中具有重要的作用，其中对于Cech 上同调以及Bredon 上同调的研究都是基于复代数簇上，而由于实数域的不封闭性，在现有的基于实系数多项式解的解析方法来研究实代数簇是很困难的，因此，有必要将其扩展到有Galois 群作用，尤其是Gal(C/R)作用的复代数簇上的上同调理论。这个对于实代数上簇的研究是非常有用的。在文献[1]中，Bredon 定义了在有限群G作 用下的等变上同调理论；在文献[2]中，May、Lewis 和MacClure 证明了由普通的整数分次的Bredon 上同调理论可以扩展到普通的RO(G)−分次的Bredon 上同调理论。本文将介绍最简单情形Gal(C/R)作用下轨道点的上同调环。

1 奇异同调和奇异上同调

1.1 整数分次的奇异同调和奇异上同调

为了将主要的结构放置在恰当的位置上，先回顾下奇异同调和上同调的传统方法，当系数为整数时，奇异同调函子被定义为是下列函子的合成。

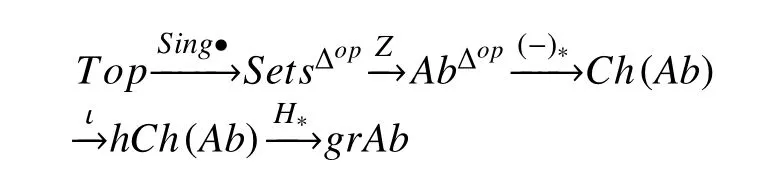
给定一个阿贝尔范畴A， 将A中复形的范畴记为Kom(A)， 复形上的边界记为Kom−(A)，从而可以得到奇异上同调群的定义[3]。

1.2 奇异同调的Dold-Thom 方法

奇异同调的Dold-Thom 方法可以看作是从一个空间X出发，生成一个简单集Sing•(X)，然后将其定义为ZSing•(X)，最后应用到链复形函子并取其同调. 关于该定理的证明，最著名的版本涉及到点空间 (X,x0) 的 无限对称乘积S P∞(X)， 从而得到X的约化同调，因为ZX是一个阿贝尔拓扑群，那么Sing•(ZX)是点态加法下的简单阿贝尔群，根据文献[4]， π∗(ZX,0)可以从下面函子的复合得到。

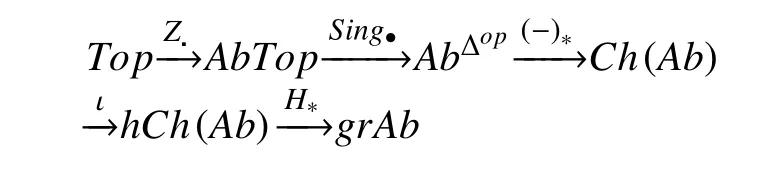
其中，AbTop是对象为阿贝尔拓扑群，态射为连续同伦的范畴。

1.3 同伦理论的奇异上同调

CW−复形同伦类型空间称为Eileberg-MacLane空间[5]，如果满足：

1.4 等变情形下的奇异（上）同调

在有限群G作用下的拓扑空间的范畴，每个轨道G/H所起的作用与通常拓扑中的某个点是一样的，但对于同调和上同调理论来说，增加了一定的复杂性，因为它们的系数不再是群了，而是从G−轨道和等变映射到阿贝尔群所构成的函子，我们把它叫做系数系统[7]。因此，要寻找整系数奇异同调群的等价对应物就会有多种途径. 其中一种合理的方式是根据1.2 中提到的Dold-Thom 方法. 而另一种方式是1.1 中提到的通过找到函子X■→[X,ZoSn]G来获得。

2 主要定义

首先，我们回顾一些本文中需要用到的相关定义. 下面的定义在文献[1]和文献[2]中都可以找到。

定义1 系数系统是指反变函子M:OG→Ab。

定义2 普通约化Z−分次Bredon 上同调理论是在范畴GCW∗，且系数系统为M的反变函子的序列：

满足下面的Eilenberg-Steenrod 公理：

1）如果范畴GCW∗中的两个映射是G−同伦的，那么诱导出上同调间相同的映射；

2）对于任意的X∈GCW∗和n∈Z，有自然同构：

是正合的；

3 单轨道点的上同调环

4 总 结