利用新教材培养高中生数学建模素养*
2021-08-31赵加营
赵加营
数学建模是数学六大核心素养之一,是高中数学课程的重要内容,在高中数学教学中占有重要地位。在《普通高中数学课程标准(2017年版2020年修订)》(以下简称“2017年版课标”)中“数学建模”的各项内容、要求见文末表1。由此可见,2017年版课标在数学建模的“课时学分、内容要求、教学提示、学业要求”等方面提出了具体、明确的指导意见,为落实新课程、实施新教材指明了教学实践路径。
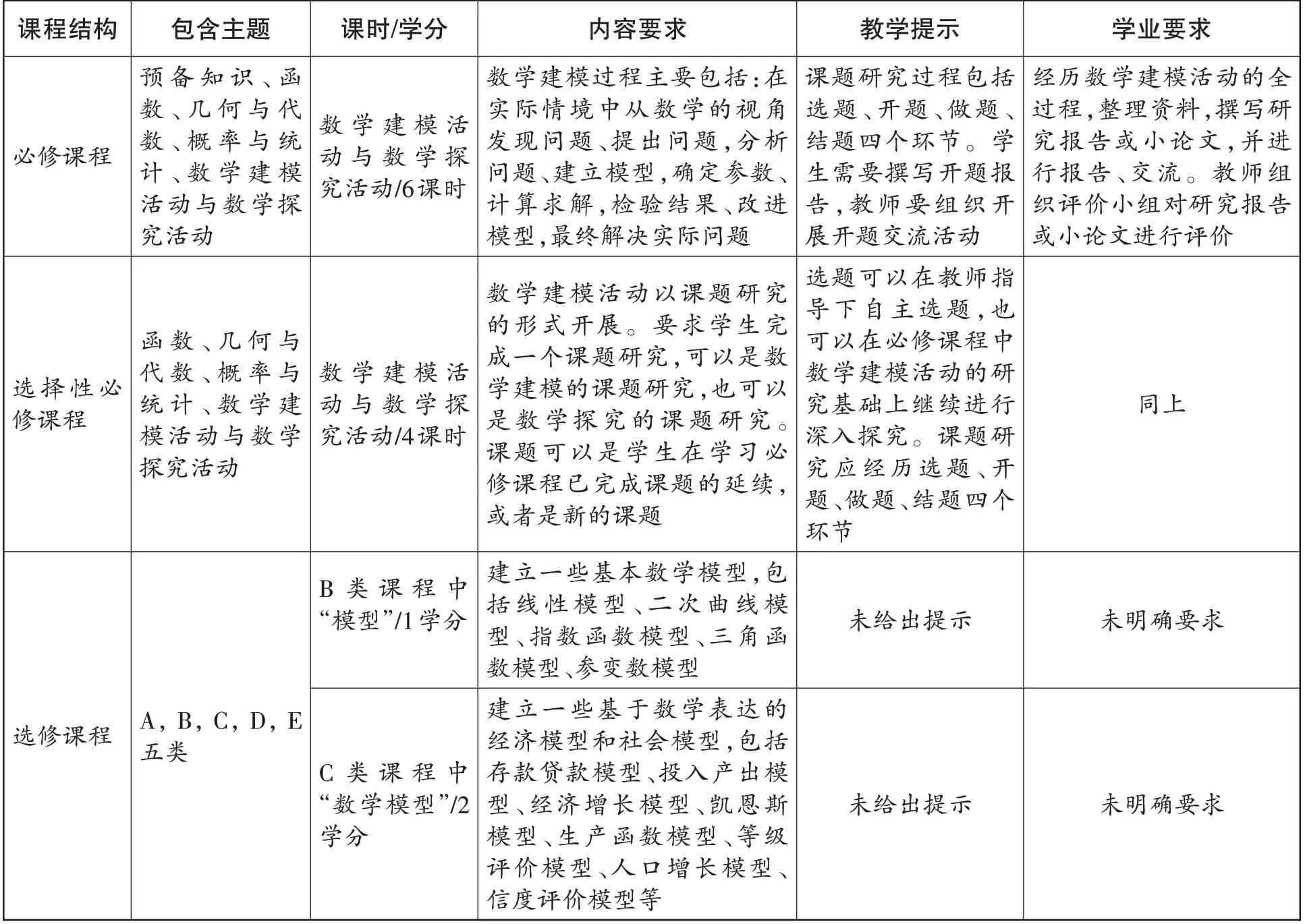
表1 数学建模的课标要求
此外,2017年版课标在附录部分还对数学建模素养做了三个水平的划分(限于篇幅,这里不再列出),这也为我们开展数学建模教学提供了依据。下面结合苏教版高中数学新教材必修一、必修二的教学,谈谈高中生数学建模素养的培养。
一、加强数学建模教学
笔者曾设计相关数学建模测评试题(见附录)来评价学生的数学建模素养,从测评结果看,学生在水平三上处于很低状态。因而,重视数学建模素养的培育,把数学建模教学常态化,是刻不容缓的现实要求。为此,我们需要做到如下两点。
首先,保障课时。依据新教材中提供的素材,参照2017年版课标的课时安排,确保数学建模教学课时到位。如必修课程中“主题五数学建模活动与数学探究活动”建议6课时,在实际教学中,“数学建模活动”应安排5课时,具体见表2。

表2 必修课程数学建模教学课时(建议)
其次,要精心设计教学。数学建模的教学准备往往要比其他教学内容花费更多时间,需要从问题背景、概念内涵、数据分析、其他学科知识等多方面查阅资料,为问题简化提供基础。在原有的数学建模水平一和水平二的教学实施基础上,应特别重视水平三的教学设计和操作实践。教师需精心设计熟悉的、关联的、综合的情境,引导学生发现和提出问题,建立合适的数学模型,准确求解模型,自觉检验模型,进而完善模型,最终分析和解决问题。教师应帮助学生积累数学建模的策略,掌握模型思想,提升解决问题能力,不断发展数学建模素养。
例如,必修一关于“体重与脉搏”的问题中只给出“动物消耗的能量E与通过心脏的血流量Q成正比,动物的体重与体积成正比”的信息,备课时要查阅资料,拟出问题:①什么是血流量?什么是脉搏率?②心脏每次收缩挤压出来的血量与心脏大小的关系?③动物心脏大小与这个动物体积的关系?④动物体内消耗的能量与身体的表面积的关系?⑤动物表面积与体积的大致关系?⑥如何在Excel中进行数据拟合?如何找到最优拟合函数?
实施本课题教学时,需从课前、课中、课后三个环节进行精心安排。
课前:让学生查阅纸质资料或电子资源,搞清以上①至⑥问题,会在Excel中作出数据的散点图,会用“添加趋势线”寻找拟合函数。
课中:出示问题,引发思考,引导学生按照“简化假设、建立模型、求解模型、检验结果”的步骤逐一完成。
课后:回顾与评价本次建模过程,总结体会其中要点,掌握重点步骤,消除难点,解开疑点,积累建模经验。例如,构建数学模型时,若所给数据较大,可以对已知数据取对数,从而使变换后的数据“均匀”,有利于发现趋势或规律。
二、开展数学建模活动
认真实施新教材的设置内容,充分保障新教材中“数学建模活动”的教学课时和训练学时,确保数学建模教学进入常态化,改变原来为应试而进行的零散、偶然、短暂的应用题教学现象。
组织学生开展数学建模的选题、开题、做题、结题活动,结合数学教学软件(如几何画板、Geogebra、Cabri 3D等)、“互联网+”等教育信息技术,开展数学实验、现场操作、实际体验、合作探究等研究活动。例如,学习“数列”后,进行存款利息、按揭贷款、理财产品等数列模型构建活动;学习“解三角形”后,进行旗杆、教学楼、电视台等高度测量活动,体验三角形模型的应用;学习“函数”后,进行一次、二次、反比例、幂、指、对、三角等函数模型构建活动;综合运用所学知识,对超市商品价格、路线最优设计、效益最大化、能耗最小化等问题进行建模活动。总之,将数学课堂之中的数学建模活动(侧重于水平一水平二的目标)和课堂之外的建模操作活动(侧重于水平三的目标)结合起来,让学生体会数学的有用、有趣、有美、有神,既提升兴趣、增强动力,又训练思维、培育素养。
三、积累数学建模课程资源
首先,深入研究新教材中有关数学建模的例题、习题,除涉及相关知识点外,充分挖掘其蕴含的数学思想、数学文化、模型结构,精心设计教学内容,做好反思评价,积累课本中的数学建模资源。在研究教材中数学建模素材的基础上,做好这些问题的拓展工作,充分发挥教材例题习题的辐射功能和母题功能。
其次,认真研究2017年版课标及“课标解读”中数学建模案例,将这些案例融入数学建模的教学中,特别是体现水平三的建模问题,根据模型系列,归纳梳理,形成数学建模资源。
最后,从数学期刊、数学应用与建模专著、数学应用竞赛、大学建模竞赛中,或直接引用,或改编改造,或简化移植,作为数学建模教学的资源。
将以上的建模教学资源,按照模型类别或教学时序,编辑成册,形成具有本校特色的数学建模校本课程,不断积累、修改、完善,为数学建模素养的达成提供课程保障。
附录
测试题1(数与代数)
(1)(由《中学数学应用与建模》第80页例8改编;水平一,记为Q11)
长为180cm的铜棒,要截成10段材料,规格是12cm,23cm两种,每种规格都要有,试找出材料利用率在95%以上的落料方案。
(2)(由《普通高中数学课程标准(2017年版)解读》第103页“水平二的问题”改编;水平二,记为Q21)
一个容积一定的无盖圆柱形罐,它的底面半径为r,高为h,问当h∶r为多少时,罐的表面积最小?
(3)(由《普通高中数学课程标准(2017年版)解读》第103页“水平三的问题”改编;水平三,记为Q31)
我们经常能在超市中看到这样的情形:同种商品会有大小不同的型号,价格各不相同,比如某品牌的牙膏有40g,120g,180g等几种质量规格的产品,价格分别为3.70元,9.30元,13.20元。试对影响商品销售价格的因素进行分析,选择主要因素,忽略次要因素,研究主要因素与价格的关系,从而得到商品价格关于牙膏质量的函数关系。
测试题2(图形与几何)
(1)(2010年江苏高考试题第17题第1问,水平一,记为Q12)
某兴趣小组测量电视塔AE的高度H(单位:m),垂直放置的标杆BC的高度h=4m,点A、B在地平面上,EC与AB相交于点D,仰角∠ABE=α,∠ADE=β。该小组已经测得一组α、β的值,tanα=1.24,tanβ=1.20。请据此建立几何图形,并算出H的值。
(2)(水平二,记为Q22)
墙上有一壁画,最高点离地面4米,最低点离地面2米,观察者从离地面高1.5米处观赏该壁画,问:观察者离墙多远时,眼睛观察壁画上下沿形成的视角最大?你能利用几何知识作出观察者的位置吗?
(3)(水平三,记为Q32)
电影作为一种消费,人们总是希望自己能坐在电影院的最佳位置,使得视觉、听觉得到最好的享受。在设计影院时,已经充分考虑了观众看电影的舒适度,对于影院的地板倾角、前后排椅子之间的距离等都经过了精心的设计。而尽管如此,不同位置看电影肯定也有很大差异,什么位置是看电影的最佳位置呢?试建立数学模型分析。
测试题3(概率与统计)
(1)(由《普通高中课程标准实验教科书数学选修2-3》习题2.4第10题改编,水平一,记为Q13)
某城市平均每10个家庭中2个家庭有小汽车。若从这个城市中任意选出5个家庭,试求2个以上(包括2个)的家庭有小汽车的概率。
(2)(水平二,记为Q23)
某高级中学要调查学生谈恋爱的比例。设计了一副纸牌,其中75张印有问题①,25张印有问题②,两个问题为:①你谈过恋爱吗?②你学生证末位号码是偶数吗?
调查100名学生,让被调查学生任意抽取1张牌(随即放回,并不让调查者知道被调查者抽到的问题,以保证被调查者给出真实的回答),学生根据牌上所对应的问题用“是”或“否”加以回答。若有18人回答“是”,学生证末位号码是偶数的概率为0.5。请估计该校学生谈过恋爱的人数的比例。
(3)(由《生活中的概率趣事》第92页问题改编,水平三,记为Q33)
某市的出租车共有3200辆,其中蓝色的有2720辆,绿色的有480辆。在一起晚上发生的肇事逃逸案中,目击者确认肇事出租车是绿色的,实验证明目击者在晚上正确分辨绿色和蓝色(正确地将绿色归为绿色,蓝色归为蓝色)的概率是80%。如果你作为法官,会采纳目击者的证词吗?请从数学角度说明理由。
