借助“主题-单元”理念教学新教材——以“立体几何初步”为例

丁左军 董裕华

“学生数学学科核心素养水平的达成不是一蹴而就的，具有阶段性、连续性、整合性等特点。教师应理解不同数学学科核心素养水平的具体要求，不仅关注每一节课的教学目标，更要关注主题、单元的教学目标，明晰这些目标对实现数学学科核心素养发展的贡献。”［1］高中数学教学要有整体观、大局观和系统化观念，帮助学生发展数学能力，提升数学素养。

“主题-单元”教学是在整体思维指导下，在整体把握教材的基础上，用全局的眼光、系统的方法，将教材中具有内在联系的知识进行整合、重组并形成相对完整、动态的教学。“主题-单元”教学帮助学生从更大的视角认识数学对象，学习数学思维方法，通过变换知识载体，从横向和纵向打通知识间的联系，实现对知识的内涵式理解和建构。对“立体几何初步”一章而言，我们可以从四个维度进行“主题-单元”设计和教学。

一、在操作实验中发展直观想象素养

空间想象素养的培养是一个不断改进和完善的动态发展过程，需要有规划、有步骤、有策略，循序渐进，可持续进行。

1.对“基本立体图形”主题单元的教学。

在本单元中，学生初步接触空间几何图形，因而可以通过从形到思来发展学生的空间想象能力。可以让学生经历如下实验操作体验。

（1）从生活情景中认识空间图形，获得整体立体图形的感知，形成初步印象；

（2）对照实物图，利用工具“再现”空间图形的生成过程，帮助学生完成对空间图形的“再认识”；

（3）通过观察3D动画到平面图形的变化，理解立体图与直观图的区别，初步认识和了解空间图形的直观图，能临摹直观图；

（4）脱离教具和样例，作出较复杂的空间图形的直观图。

2.对“空间图形中的点、线、面关系”主题单元的教学。

该主题单元中，新人教A版以平行、垂直为单元构建主线，新苏教版则以直线与直线、直线与平面、平面与平面垂直为单元构建主线。这一主题单元关涉空间想象能力发展的第二个阶段，认识点、线、面关系可以从两个方面入手。

（1）立足整体观，理解判定定理和性质定理，拓宽空间想象的范畴。比如利用直线与平面平行的判定定理判定直线与平面平行，需要寻找直线与直线平行，其实就是假定已经获得平行结论的情形下，利用性质定理寻求过已知直线的平面和已知平面的交线同已知直线平行，平面与平面垂直的判定定理的处理也与此相类似。

（2）立足大局观，变换图形观察的角度，不就事论事，就题论题，就图论图。对图形放置的位置做进一步变换，如旋转、翻转、颠倒，让学生观察和分析空间图形中位置关系的变与不变，加深对点、线、面关系的理解。同时，鼓励学生自己作图分析，图形的摆放位置也让他们自主选择。

精准确定空间图形中的直线，平面间的角度、距离关系，是空间想象能力发展的重要目标。准确定量分析角度、距离关系，在很多时候需要运用间接策略，从宏观上把握图形的特征，多角度分析，寻找突破口。

二、在概念理解中发展数学抽象素养

立体几何初步中的数学知识概念包括基本事实、推论、定义、判定定理和性质等形式。从不同的维度认识理解这些知识概念，有助于学生建立知识间的有意义联系，认清概念本质。

1.逻辑关系维度。

（1）充分必要条件角度。在学习数学知识概念时，借助逻辑命题，向学生阐明定义是充要条件，基本事实、推论及判定定理是充分条件，性质定理是必要条件。

（2）全称命题和存在性命题角度。对于直线与平面的平行、垂直的位置关系，定义、性质定理都是大前提下的全称命题，由定义到判定定理本质上是全称命题到存在性命题的演化。

2.空间与平面转换维度。

空间与平面转换的跳跃度大，有用线线垂直判定线面垂直的升维推理（由直线到平面）；有将异面直线所成角转化为平面角的降维定义（由空间到平面）；也有由“垂直于同一平面的两直线平行”联想到“平行于同一平面的两直线关系如何”的同维转化。立体几何中，判定定理一般是由线线关系到线面关系，再到面面关系的升维推导，而性质定理一般是逆向降维结论。

3.语言、图形、符号转换维度。

立体几何概念的表述一般有图形表示、文字语言表述和数学符号演示推理三种形式。概念学习中的“再认识”经历由图形感观，到文字描述，再到符号推理的过程，学生在系统学习转换中感受“概念”由具体到形象，再到数学抽象，思维不断递升。

三、在分析解决问题中发展逻辑推理素养

1.发展学生逻辑推理的层次性、多维性。

立体几何的推理论证问题，不仅有利于立体图形认识和理解的螺旋式上升，让学生不断明晰、辨清空间图形的位置关系，也有利于逻辑思维素养的不断发展。

例1：如图1，四边形ABCD是正方形，MA⊥平面ABCD，PD//MA，E，G，F分别为MB，PB，PC的中点，且AD＝PD＝2MA。求证：平面EFG⊥平面PDC。

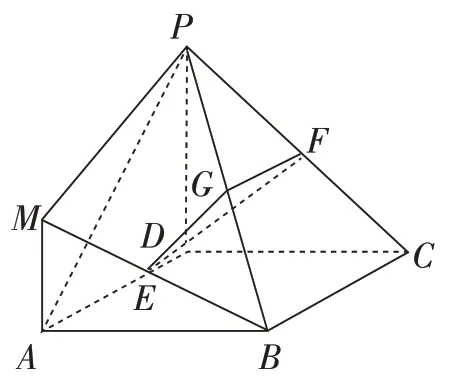
（图1）

刚接触问题时，学生感觉很难寻找到转化途径，如果跳出平面EFG和平面PDC的束缚，那么借助于BC⊥平面PDC，再由平行关系转换即可得到FG⊥平面PDC。一旦视角放大到整个空间图形，还可以选择由CD⊥平面PMAD过渡到CD⊥平面EFG，其本质在于将平面EFG延展以后，就是平行于平面PMAD的截面，上面两种思路均基于此。

2.提升学生逻辑推理的严密性。

例1的几种思路，既涉及课本的定义、基本事实和定理，也涉及课本以外的、“显然”的结论，在论证过程中合理运用这些结论就需要思维的严密性，不能想当然。平行线、平行平面转化证明垂直只能作为解决问题的思路，而不能作为理论依据。直棱柱如何运用，也是如此。与新苏教版相比，新人教A版中“空间等角定理”没有出现“异面直线的判定定理”，只定义了“空间两条直线所成角”，在论证过程中就要特别注意。

四、在实际生活中感悟生活中的数学

1.生活中的数学无处不在。

我们周围蕴藏了太多的立体图形，可以随时从生活中汲取场景发展空间想象素养。例如：为创建全国文明城市，考虑到环保和美观的要求，某地为城区街道统一换置了新型垃圾桶（如图2）。

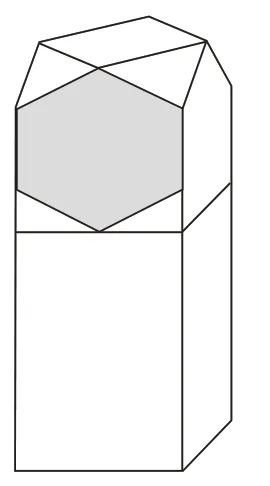
（图2）

由此“逆向”还原为数学问题：已知该垃圾桶由上、下两部分组成（上部为多面体，下部为长方体，高度比为1∶2），垃圾桶最上面是正方形，与之相邻的四个面都是全等三角形。垃圾投入口是边长为a的正六边形，该垃圾桶下部长方体的容积为______，该垃圾桶的顶部面积（最上面正方形及与之相邻的四个三角形的面积之和）为_____。

2.学而有用，学而有值。

生活中的立体图形无处不在，要让学生运用数学解决生活中的情境问题，感受到学而有用，学而有为，学而有成，保持可持续学习动力。笔者曾在课上讨论过这样一个问题：某工厂有一批边长为6m的正方形薄铝板角料，为节约成本，准备将其做成无盖的容器。请你帮忙设计：怎样裁剪，才能使容器容积最大？

学生各显其能，通过操作试验，设计了圆柱、圆锥、长方体、三棱锥等多种方案（见图3）。

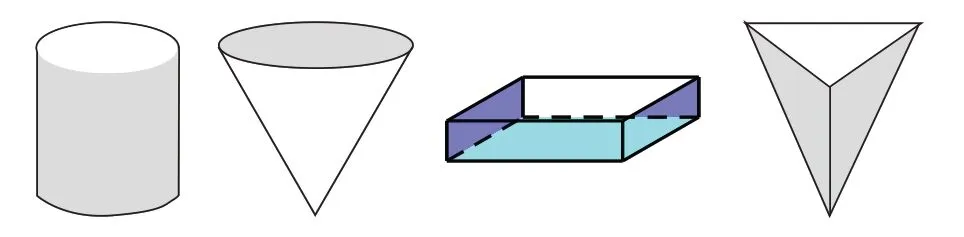
（图3）

通过亲身体验，让学生从多个层面进行思考，充分发挥了自己的想象力，设计了多种空间图形，既开阔了视野，又发散了思维。

“主题-单元”教学倡导从全局入手，细处着眼，由面踩点，又由点到面，用全局观念，系统思维解决局部知识，整体考虑，形成知识链、问题串，在知识的关联处倾注更多的注意力，有助于学生更快、更好地发现知识点的内涵与本质。