化“讲堂”为“学堂”，“动”起来的数学更精彩

安徽省合肥一六八新桥学校 孙风林

每次课后都在不断思考：如何让数学课堂更精彩，让学生在数学课堂上能激起思维的火花？如何为数学知识的产生创造探究环境？这就需要几何画板与课程的融合。应用几何画板可以创设情境、自主探究、动态呈现和解题研究，几何画板更会对教学的内容、方式和方法产生深刻影响和变革。

一、灵活使用几何画板，优化教师教学方式

动态演示是几何画板的重要功能之一。日常教学可以借助动态演示揭示数形规律，寻找数量关系，探究图形变化趋势，帮助学生提升空间想象能力。课堂教学方式的转变，有效地提高了学生的学习效果。借助几何画板，充分展示生本教育的实践效果，让学生融入课堂，通过直观操作、观察、分析生成新知。

例如，在教授九年级上册“探究二次函数的性质”新课时，我用几何画板开展了这样的教学：

1.改变参数a的数值和符号，观察二次函数图像如何变化？

2.改变参数b的值，观察二次函数图像如何变化？

3.改变参数c的值，观察二次函数图像如何变化？

4.从左到右拖动函数图像上的动点A，观察点A的横、纵坐标如何变化？

5.改变动点A的位置，观察点A的纵坐标的变化特点。

通过《几何画板》演示，展示变化规律，启发学生思考，总结生成新知。教学中拖动点A，观察参数a，b，c的变化规律，点A的坐标变化满足何种规律？改变参数a的值，观察抛物线的开口大小、开口方向如何变化？如果只在x轴上方反复改变参数a，学生经过观察、比较，不难发现得到：a>0 时，抛物线的开口方向向上；a的值越大，抛物线开口越小，a的值越小，抛物线开口越大。如果改变b，c的值，函数图像怎么变化？学生分小组，在平板上动手实践，验证自己的发现，改变了“教师单纯讲解，学生被动接收”的模式，实际检测效果很好，学生也喜欢参与课堂的探究。

又如，在学习网格中“位似图形”时，为了让学生可以更好地理解图形变化的规律，制作如下课件，辅助教学：

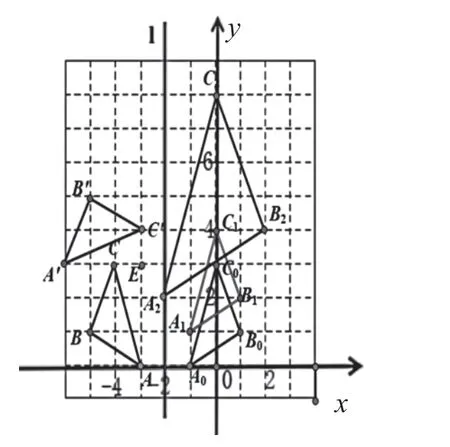
如图，在边长为1 个单位长度的小正方形组成的网格中，给出了格点△ABC、直线l和格点。

（1） 画 出△ABC关 于 直 线l成 轴 对 称 的△A0B0C0。

（2）画出将△A0B0C0向上平移1 个单位长度得到的△A1B1C1。

（3）以格点O为位似中心，将△A1B1C1作位似变换，将其放大到原来的2 倍，得到△A2B2C2。

在所有的模型设定下，其他解释变量估计系数的正负情况始终保持一致，表明回归结果是稳健的。回归系数结果表明全要素生产效率更高、资产规模更大、年轻有活力的民营上市公司更容易参与对外直接投资。高资本产出效率的企业特征在一定程度上证实了对外直接投资企业重视生产技术和学习效应。

（4）画出以E（-3,3）为旋转中心，顺时针旋转90 度得到的△A'B'C'，并求出B'的坐标。

在本节课教学中，教师打破传统的教学模式，融入信息技术，利用《几何画板》的演示功能，学生分小组探究，感受每种变化带来的坐标变化规律，积极解决自己心中的疑惑。在这个教学过程中，教师的组织引导完全基于课堂中学生的学。

二、利用几何画板功能，改变学生学习方式

数学家华罗庚说：“数缺形时少直观，形缺数时难入微。”几何画板弥补课堂中难以体现数形结合的不足，让学生在直观想象中寻找自己的答案，在动态变化关系中探寻其中不变的规律，更培养了学生用数学的眼光审视我们的生活现象，用数学的知识解读我们的生活常识。

例如，“勾股定理”第一课时的教学中，如何让直角三角形三边关系直观地呈现在学生面前？我用几何画板制作了演示课件，利用毕达哥拉斯树的动态效果展示数学的美，激发学生探究新知的欲望。学生带着疑惑和问题开始本节课的学习。本节课设计打破正常思路，首先探究三个正方形面积之间的关系，解密勾股定理内容，然后由勾股定理的数学表达式联想出推导方法，最后从理论上设计图形说明勾股定理成立。课堂上学生有探究的热情，有深度思维拓展延伸，有短暂的思维火花，精彩纷呈，高潮不断，学生享受其中的快乐，感悟数学的魅力。

在常规教学中，用圆规、三角板绘制的几何图形是静态的，要认识数形之间的关系和变化规律，需要教师用语言进行描述，设置问题启发学生思考，帮助学生理解和想象生成新知。而几何画板绘制的图形具有动态性，学生在动态变化过程中研究数量关系，在实践中产生数学结论，达到教学目标。

三、利用几何画板功能，提升教师对试题的研究能力

例如，在讲解安徽2016 年压轴题时，我进行下面的探究：如图1，A，B分别在射线OM，ON上，且∠MON为钝角，现以线段OA，OB为斜边向∠MON的外侧作等腰直角三角形，分别是△OAP，△OBQ，点C，D，E分别是OA，OB，AB的中点。

图1

（1）求证：△PCE≌△EDQ；

（2）延长PC，QD交于点R。

①如图2，若∠MON=150°，求证：△ABR为等边三角形；

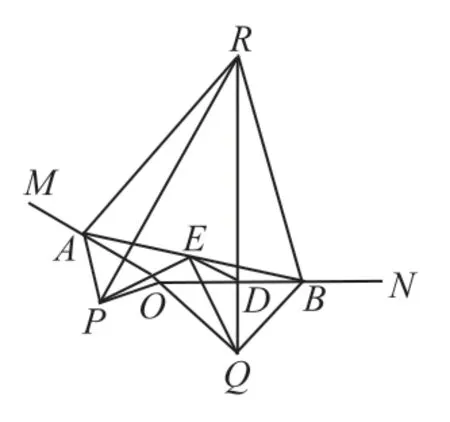
图2

②如图3，若△ARB∽△PEQ，求∠MON的大小。

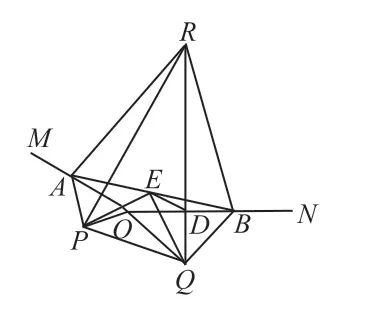
图3

这是一节面向老师的简短讲座，主题是“如何利用几何画板的动态功能，解决几何综合题目的探究问题？”当年这道中考题得分率很低，因为图形比较复杂，学生找不到其中的数量关系。面对这个问题，借用几何画板的画图功能，从最简单的图形画起，一个一个条件添加，每添加一个条件会带来什么结论？哪些结论不因为图形的改变而变化？最终添加上所有条件，产生了八个结论。中考题就是从中选择三个结论成为压轴题，最后改变图形的形状发现实际来源于教材中的一道习题。通过演示探究过程，揭示如何命制一道综合性试题，后来在教学中给学生分析这道中考题时，我也一步一步呈现，学生理解较好，思路逐渐清晰。课堂总结时，学生感慨原来数学的压轴题是这样编写出来的。借用几何画板还原问题的原生态，找到解决的方法，完全符合数学核心素养的要求。

几何画板将冰冷的数学知识转化成充满活力的数学活动，可以为数学教学打开另一扇窗，为课堂从“讲堂”变为“学堂”提供科技支持，为老师从“教过”到学生的“学会”增添了新的帮手，更为师生在数学领域开辟了新的研究通道，展示了数学的美。