“涌现性的生成”：在碰撞中触发，在跟进中迭代

马丽丽

摘要：在“社会化学习”的课堂上，生成性资源不断涌现。其原因主要有：更充沛的交互时间，让大量观点因汇聚而涌现;多民主的交往环境，让深层理解因联结而涌现;开放性的交流话题，让多元想法因差异而涌现;群体性的学习评价，让更多智慧因共进而涌现。面对“涌现性的生成”，教师还需要及时跟进、引导。具体策略有：置顶核心问题，探寻数学本质;聚焦共性问题，挑战认知盲区;联结零散问题，完善认知结构;捕捉隐性错误，提升认知精度。

关键词：“社会化学习”;生成;涌现;触发机制;跟进策略

在“社会化学习”的课堂里，学习不再是一个线性的、封闭的过程，而是一段充满未知和不确定性的奇妙旅程。学生在“学习地图”（学习单）的指引下，与同伴交往、碰撞、合作、共进，因此，大量的生成性资源不断涌现、不断迭代。可以说，“涌现性的生成”既是“社会化学习”的关键要素，也是“社会化学习”的最大魅力所在。

一、“涌现性的生成”的基本内涵

“涌现”一词，在现代汉语中的意思是“人或事物大量出现”，一般指新生事物的起源。复杂的事物大多是由微小而简单的事物发展而来的，比如，小小的种子可以成长为各式各样复杂的生物体，简单的规则可以衍生出非常复杂的游戏。涌现的本质是由小生大、由简入繁。

借用网络科学来理解，当一些人聚在一起时，总会或多或少地出现新的、不是从他们的原有性质中可以明显推出的现象。比如，虽然单只蚂蚁的能力有限，但是整个蚁群却能展现出非凡的能力。

整体大于各部分之和，这就使得涌现给人以神秘且似是而非的印象。再加上涌现无法预料、出其不意，就显得更加具有诱惑力。

“社会化学习”中的“涌现性的生成”，指的是不同的学习个体带着自己的原有认知，相互分享、碰撞、对话，新的想法和理解有可能在碰撞中生成，新的问题和困惑有可能在对话中生长，新的结构和框架有可能在梳理中建构，新的信念和思想有可能在对峙中产生。

二、“涌现性的生成”的触发机制

虽然在以往的课堂上，也會出现一些教师预设之外的生成性资源，但是我们发现，在“社会化学习”的课堂上，生成性资源出现的频率更高、内容更深刻也更丰富。为什么“社会化学习”会触发“涌现性的生成”呢？

（一）更充沛的交互时间，让大量观点因汇聚而涌现

在传统的课堂中，学生大多数时间是相对独立的学习个体，他们更多的是在倾听和操作，彼此之间很少交流观点。在这样的课堂里，学生会处在相对浅表的学习状态中，学习被边缘化，生成性资源必然很少，更不用说“涌现性的生成”了。

在“社会化学习”的课堂中，我们通过延长时间，诱发生生之间深度的交互。每节课上都有近20分钟的时间让学生处于“自组织”的状态，他们依据学习单展开共同学习。而教师“暂时缺席”，不再介入干扰他们的学习。足够长的时间，避免了讨论匆匆走过场、才开始就结束的尴尬，使得每个学生都可以更耐心地倾听、更沉浸地思考、更多维地互动、更深入地对话，不同的观点可以不断汇聚、交织、碰撞。这样的过程显然比传统的课堂更有利于新观点的生成。这就好比阿基米德想到测量皇冠体积的方法，表面上看是灵光一现，但实际上是长时间思考后的顿悟，需要一个由量的积累到质的突变的过程。

（二）多民主的交往环境，让深层理解因联结而涌现

在传统的课堂中，很多生生对话是由教师发起、撬动的，参与交流的往往是一些自信的、外向的、敢于表达、乐于表达的学生。除此之外，那些“沉默的大多数”，依然畏惧面对全班表达自我，会担心因说错而“丢面子”，会纠结自己的回答能否得到教师的肯定评价。

在“社会化学习”的课堂中，共学小组一般只有4—5人，小组交流时没有教师的参与，即便有组长，其承担的角色也只是“组织者”，而并非“权威”。因此，如果有人表达了不同的想法，那么大家会互相讨论、共同商量着解决问题，进而达成共识。也就是说，每个人的想法，不论对错，都是在为本组的学习联结作出积极的贡献。在这样的交往环境和评价导向下，学生处于心理的安全舒适区，可以更大胆地表达内心更真实的想法，暴露更多的“学习隐私”。这样也就更有利于学生在小组里产生更丰富的观点，获得更深层的理解。

（三）开放性的交流话题，让多元想法因差异而涌现

在“社会化学习”的课堂中，学生交流的话题往往比较开放。这是因为：首先，教师在规划学习路径时，会在学习单上有意识地设计一些适度劣构、适当留白的开放性问题，以撬动组内共学时的生生对话;其次，教师会在学习单上设计一个“提问”环节，让学生自由提出自己的疑问，来自学生的真问题往往会引起小组成员的共鸣，而且有的问题没有标准答案。这样的问题能引发学生多角度、差异化的思考，再加上学生长时间地处于深交互、强反馈的状态中，彼此之间便会不断碰撞出思维的火花，迭代出新的想法。

（四）群体性的学习评价，让更多智慧因共进而涌现

在“社会化学习”的课堂中，每个小组都是一个和谐共进的团队，其学习成果是群体性的。我们引导学生思考如何让自己和同伴都学得更好，倡导学生在意整个小组对某一问题的认识和理解是否得到推进与扩展，关注团队的共同成长。为了让同伴学得更好，让团队共同成长，学生被倒逼着产生更多智慧——或积极画图，以直观助力同伴思考;或友情提醒，借提示优化同伴理解;或积极追问，借提问驱动同伴深入;或多元解答，以差异满足同伴需求……这样一种群体性、成长型的评价机制，让这“一群人”手拉手共同前进。

三、“涌现性的生成”的跟进策略

面对“社会化学习”的课堂中“涌现性的生成”，教师还需要及时跟进、引导。毕竟，并非所有的生成性资源都是正确的、完善的。如何提供支架攻坚克难、如何顺水推舟纠偏容错、如何乘势而上放大价值……都需要教师运用自己的教学智慧。当然，教师的跟进不适合安排在组内共学阶段，以免打扰学生“连续性的进程”，可以安排在组内共学后的全班交流环节。具体可以采用如下策略：

（一）置顶核心问题，探寻数学本质

在网络社区或论坛中，博主或版主会把一些高质量的讨论帖“加精”，或把一些重要的内容“置顶”，以引发网友的群聚性关注。在“社会化学习”的课堂中，教师也可以借鉴这种方法。数学教学不论采用何种方式进行，都不能囿于让学生知道结论与简单运用，而要与学生共同探寻结论（现象）背后的原理（本质）。如果组内共学中出现了直指数学本质的核心问题，教师可以果断将其“置顶”，引发全班学生的群聚性关注，引导学生乘势而上探寻数学本质、感悟数学思想、建立数学模型，从而放大核心问题的价值，提升学生思维的深刻性。

例如，教学“一个数乘10、100、1000……的计算规律”这一内容时，教师从组内共学中涌现的诸多问题中甄选了以下两个问题——

1.为什么整数乘10、100、1000……是在末尾添0，而小数是移动小数点呢？

2.为什么小数点向右移动，这个小数就会乘10、100、1000……？而且，为什么是乘10、100、1000……而不是乘其他数呢？

将其作为重点，引导学生讨论——

生我觉得，因为整数没有小数点，所以它乘的那个数末尾有几个0，就在整数末尾添几个0。

生你说得很有道理，但是整数并不是没有小数点，只是没写出来。我觉得，在整数的末尾添0，就相当于把前面的数往前挤了，所以它就扩大了。

师你的“往前挤”是什么意思？

生（出示图1）比如，5本来在个位，添了一个0之后，就被挤到十位上去了;添两个0，就被挤到百位上去了。

生如果顺着你的思路来想，那么小数点向右移动一位，也相当于把数往前挤了。（出示图2）比如，5.04的小数点向右移动一位，5原来在

个位，现在变到了十位，0从十分位变到了个位，4从百分位变到了十分位。每一个数都乘了10，5.04就乘了10。

师看来，不论是在整数末尾添0，还是将小数点向右移动，都是为了“挤数位”呀！那为什么扩大的倍数是10、100、1000……呢？

生（出示图3）因为我们采用的是十进制计数法，相邻计数单位之间的进率是10，所以只要往左挤一位，就乘了10。

这里，教师遴选出的两个核心问题都指向规律背后的原理，同时还打通了整数与小数之间的本质联系。

（二）聚焦共性问题，挑战认知盲区

虽然每个学生的学习基础和认知水平不同，会提出不同的问题，但是，很多个性的问题通常会在组内“共学”中得到解决，而需要向全班“求助”的往往是一些共性问题。这些共性问题一般具有“拓展性”，来自学生的心灵深处，触及学生的认知盲区，是教师应当支持学生学习、帮助学生挑战的地方，也是学生提升思维品质、拓宽认知边界的契机。对此，教师引领学生一起刨根问底、审视辨析，共同走向思维和认知的深水区，也许就会柳暗花明、豁然开朗，看到别有洞天的风景。

例如，教学《圆的认识》一课时，教师发现，各个小组在质疑深化环节“神同步”地发出了令人怦然心动的“灵魂三问”——

1.在同一个圆内画出的所有线段中，直径是最长的吗？为什么？

2.圆究竟是有无数条边、只有一条边，还是没有边？

3.在同一个圆内，半径的条数比直径多？还是一样多？

这三个问题对于学生感受理解圆的特点，都是很有价值的。问题1来自学习单，学生在组内共学中“不知其所以然”，教师可以提供学习支架，引导学生从“三角形三边的关系”来理解直径是圆内最长的线段。问题2是学生在组内共学中生成的，他们感受到圆是由曲线围成，又想象着圆可以由正多边形不断“切割”而来，教师需要帮助学生厘清困惑的原因，即对于“边”的界定。问题3蕴含着有限和无限的思想，教师可以在课后结合康托尔的“神奇的旅馆”进行拓展，让学生感受到不能用有限的思维方式来思考无限的问题。

（三）联结零散问题，完善认知结构

学生中涌现出的问题与困惑，其“出厂设置”往往是散乱的、无序的。这样的呈现方式会给后续的讨论带来难度：要么难沉潜，东一榔头西一棒子;要么易跑偏，走着走着忘了为何出发。因此，教师要做好问题的梳理与联结，变散为连、化零为整。这样，不仅可以让学生的讨论随着问题链的“导航”不断推进，完善认知结构，还能起到“棍扫一大片，枪挑一条线”的“团灭”效果。

例如，教学《用一一列举的策略解決问题》一课时，笔者在学习单中设置了如下研究问题：

1.南山中心小学举行小学生足球赛，有4支球队参加，分别是红队、黄队、绿队和蓝队。如果每两支球队比赛一场，一共要比赛多少场？你能用不同的方法解决问题吗？

2.一列火车从上海到扬州，中途要经过4个站，这列火车要准备多少种不同的车票？

3.结合上面两道题的解答过程想一想：怎样列举可以做到不遗漏、不重复？把你的好方法写下来，与同学分享。

梳理学生的学习单时，笔者发现，许多细碎的小问题看似散乱，但大致可以归整为两个方面，即“解决问题”与“策略感悟”。果然，在组内共学后，学生提出了许多悬而未决的问题——

生（来自小组1）我们组有两个问题：第一个，第1题，小王同学的方法是“4-1+2+1”，我们大家都看不懂;第二个，当数据比较多、比较大的时候，列举还有效果吗？

生（来自小组2）我总结出一个公式来解决这类问题，即（n-1）+（n-2）+（n-3）+…+（n-n），但我们不知道它是否可行？

生（来自小组3）第2题，火车从上海到扬州，回来就是扬州到上海，到底要不要乘2呢？

生（来自小组4）我们组想要补充：是否每次都要画图？如何快速简洁地知道有多少种组合？

简单梳理各小组的问题，可以发现：第一个小组的第二个问题和第四个小组的问题都是关于“策略价值”的，说明学生对列举策略并不认可，觉得是个有点“笨”的办法，没有真正体会到列举策略的价值所在;其他问题则说明学生列举不得法，解题有困难。这样归整后，教师就不会被学生看似七零八落的问题牵着鼻子走了，可以按照“解题→方法→策略”的顺序推进教学：先正确解决问题，再体会分类列举、画图列举的优势，最后点破列举策略的真正价值，引领学生不断深入，完善认知结构。

（四）捕捉隐性错误，提升认知精度

除了学生主动提出来的显性问题，教师也不要忽略生成性资源中的隐性错误。毕竟，生成性资源并不全都是正确的，也会有错误的细节、跑偏的思路混在其中。这些隐性错误往往在“闪现”之后就被学生忽略了，需要教师及时捕捉，引发认知冲突、辨析释疑，从而提升学生的认知精度。为了让隐性错误浮出水面，教师可以提出一些解释性问题，让学生对自己的答案加以分析，暴露真实的思维过程。之后，可以提出一些挑战性问题，引导学生统一思考方向、厘清矛盾焦点，便于同伴之间“集中火力”辨析。

例如，教学《三角形面积计算的练习》一课时，笔者在学习单中设置的研究问题第1题如下：

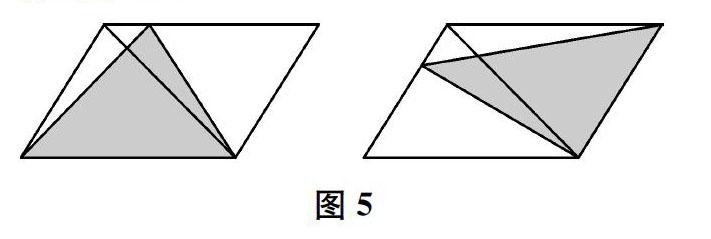
下页图4中两个平行四边形的面积都是50平方厘米，两个涂色三角形的面积相等吗？为什么？

有关此题的一个教学片段如下——

师在组内共学时有遇到问题吗？

生我们组对第1题的意见不统一。小李同学认为，这两个三角形不等底、不等高，所以面积不相等。其他人认为，面积是相等的。

师其他组的同学有什么看法？

生我认为，是相等的，因为这两个三角形都和平行四边形等底等高，所以面积都是它的一半。

生（展示其学习单中的图，见图5）我把三角形的顶点平移了一下，都移到最边上，这样就能看出来了。

生我也想画个图。（出示其学习单中的图和解答，见图6）我们可以平移，把两块空白部分合并一下，这样就会发现，三角形的面积是新平行四边形面积的一半。

师每个三角形的面积都是平行四边形面积的一半，所以它们面积相等。不过，小李同学似乎是另一个思路？

生这两个三角形虽然不等底、不等高，但就是底和高互换了一下，所以面积还是相等的。

（学生沉默一会儿。）

生（多位，举手）不对！不对！

生（同步指图）左边三角形的底是平行四边形的这条边，而右边三角形的高是这样一条垂直的线，它们不是互换的关系。

（多数学生恍然大悟。）

这里，关于“两个涂色三角形的面积是否相等”这一问题的讨论，不同方法、不同结论糅杂在一起。有的学生是错误的结论掩盖了正确的想法，如“这两个三角形不等底、不等高，所以面积不相等”;有的学生则是正确的结论掩盖了错误的思路，如“这两个三角形就是底和高互换了一下，所以面積还是相等的”。针对这样细微的、易被忽略的错误，教师组织学生充分讨论，通过精准的辨析让学生理解得更清晰、更通透。

最后，需要说明的是，一段时间的课堂实践中，学生的“涌现性的生成”深深地打动、吸引着笔者，也让笔者意识到：一些本原性问题不应被回避或悬置，教师要在备课时，把教学内容中最为原始、最为朴素、最为本质的思想、方法想通透、理明白，并在课堂上伺机而动，或以问题回应，启发火热的思考;或搭设脚手架，提供突破的方向;或清晰地讲解，拨开云雾……如此，才能不负“生成”不负“卿”。

参考文献：

[1] 王帆.微时代“社会化学习”本质探寻[J].中国电化教育，2014（8）.

[2] 马里奥·邦格.涌现与汇聚：新质的产生与知识的统一[M].李宗荣，李成芳，等译.北京：人民出版社，2019.

[3] 约翰·霍兰.涌现：从混沌到有序[M].陈禹，等译.上海：上海科学技术出版社，2006.