工业遗产再利用开发的关键路径研究
2021-08-30高祥冠
高祥冠
(太原科技大学 艺术学院,山西 太原 030001)
一、引言
在城市转型发展和工业遗产开发热潮的背景下,国内学者对工业遗产开发的研究热度迅速提高[1]。我国的工业遗产研究主要集中在对工业遗产保护和利用的研究和工业遗产旅游开发方面[2]。王建国,王建国和蒋楠(2006)[3]分析列举了在中国实施保护和改造再利用研究的基本内容,指出经由对产业类历史建筑及地段实践层面上的实证研究,提出具有现实技术针对性的改造设计方法、评估原则和技术规范要点为中国当前之必须。张立峰和鹿嘉(2010)[4]研究了大连工业遗产旅游的动力机制,认为动力有内在因素、外在因素和催化要素三方面,并以此为基础构建了开发的动力模型。这些研究为我国今后的工业遗产再利用开发提供了良好的理论和实践基础。但是,工业遗产的再利用开发,具有主体权属复杂性、利益主体多元性、开发过程不可预见性等复杂特点,保证工业遗产的更新和再利用开发不滞后,让项目管理者更好的调控监督工业遗产再利用开发的流程规划,保障项目的顺利交付,本文正是以此为研究出发点,使用关键路径分析法,做探索性的研究。
二、工业遗产开发的关键路径研究意义
(一)关键路径分析与其研究发展
自从20 世纪50 年代以来,关键路径法(Critical Path Method,CPM)在项目管理领域得到了广泛的应用和发展[5-6]。关键路径法是一种网络分析技术,在计划评审法的基础上,从项目网络图中寻找到一条决定整个项目开发用时的路径,确定开发项目的所需时间,判断开发项目的每个活动的松弛,从而可以根据实际用时情况和拥有的资源情况,更好地安排和控制项目的进度。
第一次世界大战期间美国法兰克福兵工厂的亨特·甘特(H.Gantt)在安排生产和开展计划管理的过程中首先发明并使用的甘特图,甘特图是最早的项目工期计划与控制的方法和工具[7]。20 世纪50 年代后期,传统的甘特图、协调图等方法在解决复杂项目的计划和控制问题时遇到了极大的阻碍,美国军方和各大企业纷纷为管理各类项目寻求更为有效的计划和控制技术[8]。1957 年美国杜邦公司在兰德公司的合作下开发出了CPM 方法,1958 年美国海军为研制“北极星导弹潜艇”,使用CPM 协调了11 000 多家单位参与了该项目研制工作。通过从数学和统计学等方面来研究大规模工程建设的有关计划和管理,提出了CPM 方法[9]。CPM 方法的出现,不仅极大地促进了系统工程科学的发展,而且使第二次世界大战中发展起来的运筹学得到了充实。CPM 也由最初的只应用于解决任务活动时间确定,无资源约束的简单问题,逐渐发展到解决任务活动时间不确定,带资源约束的复杂问题[10]。同时,CPM由最初的航空、国防、建筑等领域广泛普及到各行业的项目管理工作[11]。70 年代以来,随着计算机技术的发展,仿真分析方法在项目管理问题的研究中得到了广泛的应用,如虚拟设计团队[12-14]、贝叶斯风险分析[15-16]、任务规划算法优化[17-18]等等;逐步把最初的工作计划评审和关键路径分析与系统论、经济学、管理学、行为科学、心理学、计算机技术等结合起来,逐渐发展成为一门较完整的项目管理学科体系。
(二)工业遗产开发的关键路径分析研究意义
通常,工业遗产的开发涉及土地权属、资产归属、环境安全、投资主体、相关利益群体、项目改造设计、项目运营等诸多内容,因此,一般都会出现严重的项目开发流程滞后。由于工业遗产的综合开发庞大而复杂,前期的项目管理规划尤为重要,项目管理者必须将开发活动的计划和流程安排进行科学的设计。为了使整个项目按时完成,研究者必须对众多的工作或活动进行适当的安排和协调,此时,关键路径法就显得至关重要。CPM 在综合开发项目领域的研究与应用已经有了相当的发展。Law博士[19]从可视化的角度,认为CPM 和项目网络结构可以为项目任务以及项目组织的建模提供技术与工具支撑,能够直观地展现任务之间以及项目组织之间的相互关系。齐二石和姜琳(2008)[20]将大型工程项目的复杂性归纳为时间复杂性和空间复杂性,并针对其管理问题提出了信息集成、过程集成、参与方集成的集成化管理的思想。晏永刚等[3-4]进一步研究了大型工程项目的整体性、开放性、动态性、多层次性和自组织性,进而运用综合集成方法体系。但是,对于工业遗产的综合开发,CPM 的相关研究还处于起步阶段。本文使用关键路径法对工业遗产再利用开发做探索性的研究。
三、工业遗产开发的关键路径分析
(一)项目活动安排与项目网络图的构建
研究工业遗产开发的关键路径,首先需要细分开发项目的各项活动,并且确定各项活动的先后顺序。在不考虑工业遗产的环境治理的情况下,表1对20 项开发活动进行了描述,并注明了各项活动的紧前活动(immediate predecessor)。对于给定的活动,只有其紧前活动栏中列出的活动都已完成,该活动才能开始进行。
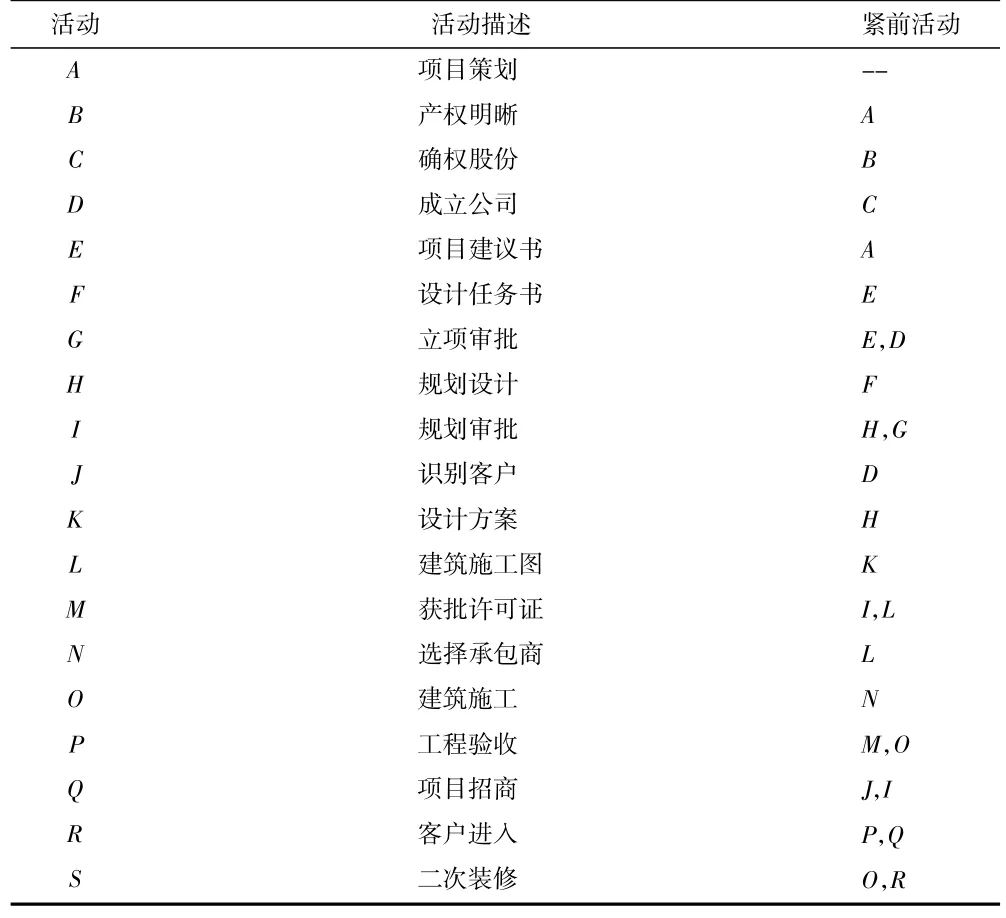
表1 工业遗产再利用的活动列表
根据表1 的信息,图1 构建工业遗产再利用的项目网络图(project network)。网络中的节点代表每项活动,箭线代表各项活动之间的优先顺序。此外,网络中还添加了两个节点,表示项目的开始和结束。项目网络图是关键路径分析的基础,它能够形象地表示各项活动之间的先后关系。

图1 工业遗产再利用网络图
(二)项目活动用时的估算
在设计了项目网络图之后,需要确定完成每项活动所需时间,并以此确定完成项目所需的总时间。对于一般性的项目活动,通常可以依靠经验和历史数据,准确估计活动时间。然而,对于工业遗产再利用的综合开发,要确定这些活动的完成时间是非常困难的,最好能够用适当的值域来描述。在不确定活动用时的情况下,本研究使用乐观时间、最可能时间和悲观时间三个经验时间来描述完成每项活动的时间,并通过公式(1)计算求得每项活动的期望时间t(expected time),t将当作一个相对参考值来确定工业遗产再利用的开发用时。

其中:
a,乐观时间(optimistic time),为活动顺利完成的最小时间;
m,最可能时间(most probable time),为活动一般状态下完成的最可能时间;
b,悲观时间(pessimistic time),为活动遭遇重大延误时完成的最大时间。
工业遗产再利用开发中各项活动的乐观时间、最可能时间和悲观时间列于表2。对于活动A,其最可能时间为5 周,活动A 的实际活动时间将在4 周(乐观时间)和8 周(悲观时间)之间波动。通过公式(1)计算活动A 的期望时间t为5.3 周。
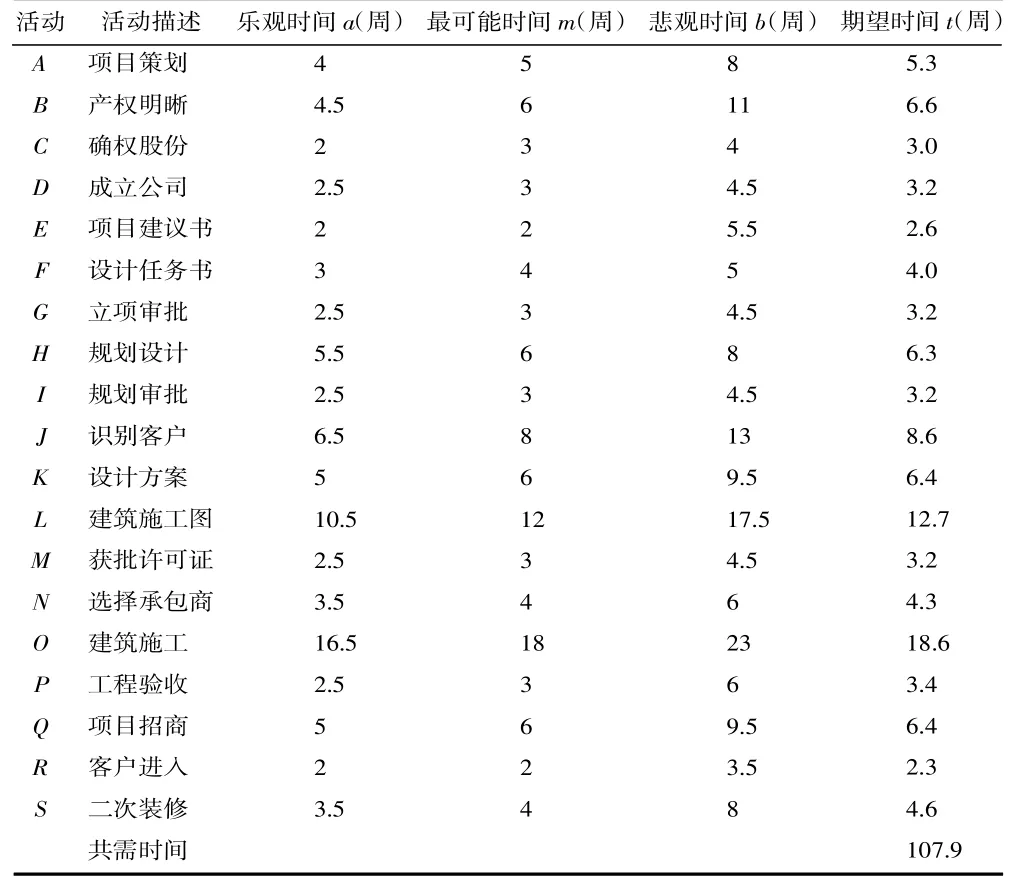
表2 工业遗产再利用活动用时表
将表2 中求得各活动的期望时间视为固定值或已知量,计算出各项活动的期望时间累加之和为107.9 周。由于存在两项或多项活动可以同时进行,实际开发用时并不需要107.9 周。在已知项目网络图和每项活动期望时间的情况下,可以使用关键路径分析法寻求出关键路径,并确定项目开发的实际用时。
(三)确定关键路径
为了确定完成工业遗产再利用开发的时间,必须对项目网络图进行分析,并找出网络中的关键路径(critical path)。路径(path)就是从起点到终点之间相连节点的序列。为了完成整个项目,必须经过网络中的所有路径。由于其他路径持续时间都相对较短,因而最长用时路径就决定了完成项目所需的全部时间。如果最长用时路径上的活动延误,那么整个活动完成的时间就会延误,因此最长用时路径就是整个项目的关键路径。整个关键路径的活动用时之和,也是整个项目的活动用时。
根据图1 得出工业遗产再利用从起点到终点的所有路径,将路径中各项活动的期望时间累加之和记为该路径的期望时间,结果列于表3。完成工业遗产再利用开发共有9 条路径,其中路径6A-E-FH-K-L-N-O-P-R-S期望时间为70.5 周,最长的路径,即项目策划——项目建议书——设计任务书——规划设计——设计方案—建筑施工图——选择承包商——建筑施工——工程验收——客户进入——二次装修是关键路径。T来表示关键路径中所有活动期望时间之和,如公式(2)所示。

表3 工业遗产再利用活动路径用时表

虽然关键路径是各条路径中历时最长的路径,却表明了关键路径上的活动不容许有延误。关键路径上的活动为关键活动,关键活动是没有时间松弛的,如果这些活动未能按时开始或按时结束,项目将会拖延。非关键路径上的活动为非关键活动,这些活动有一定的时间松弛。求得时间松弛,首先要确定网络中各项活动的最早开始时间ES(earliest start time)和最晚开始时间LS(latest start time)。对于各项活动,最早完成时间EF(earliest finish time)为:

设定活动A的最早开始时间ES为0。由于每一活动在其紧前活动没有完成的情况下是不能够开始的,所以每项活动的最早开始时间等于其所有紧前活动的最早完成时间。在项目网络图中向前推进(forward pass)线路,可以求出每项活动的最早开始时间(ES)和最早完成时间(EF)。然后,再利用向后逆推法,求出每项活动的最晚开始时间(LS)和最晚完成时间(LF)。确定各个活动的松弛时间是(LSES),所有松弛都为0 的活动即关键活动,由关键活动组成的路径就是关键路径。开发活动时间表如表4 所示。

表4 工业遗产再利用的开发活动时间表
表4 研究表明工业遗产再利用的关键路径为A-E-F-H-K-L-N-O-P-R-S,即项目策划—项目建议书——设计任务书——规划设计——设计方案——建筑施工图——选择承包商——建筑施工——工程验收—客户进入——二次装修。
由上分析,通过关键活动确定的关键路径与通过最长用时确定的关键路径得出的工业遗产再利用的关键路径是一致的。
(四)项目完成时间的概率计算
由于本研究的前提是各项活动为不确定活动时间,因此讨论项目在特定时间完成的概率就成为非常有意义的管理信息。TP为工业遗产再利用开发的总计划时间,设TP服从正态分布,利用公式(4)求得z值,再对应正态分布表,可求得项目完成时间为TP时的项目完成的概率。
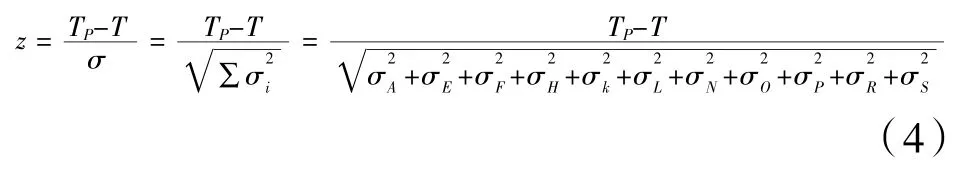
其中:σ为工业遗产开发项目关键路径的标准差,代表关键路径各活动方差之和。对于时间不确定的活动,用方差σ2来描述活动时间值的差异,可以用公式(5)计算。悲观时间(b)和乐观时间(a)经验值的差异大大影响了方差的值,两者之间的差异越大,说明活动时间的不确定性越大。

当TP=T=70.5 周,计算z=0.00,查表可知,70.5周完成工业遗产再利用开发的概率为0.5。用A、M、B分别表示关键路径上各项活动的乐观时间之和、最可能时间之和、悲观时间之和,其值可用公式(6)、公式(7)、公式(8)表示。使用公式(4)计算当TP分别等于A、M、B这三个时间下z值,并查表得相应时间的项目完成概率(见表5)。

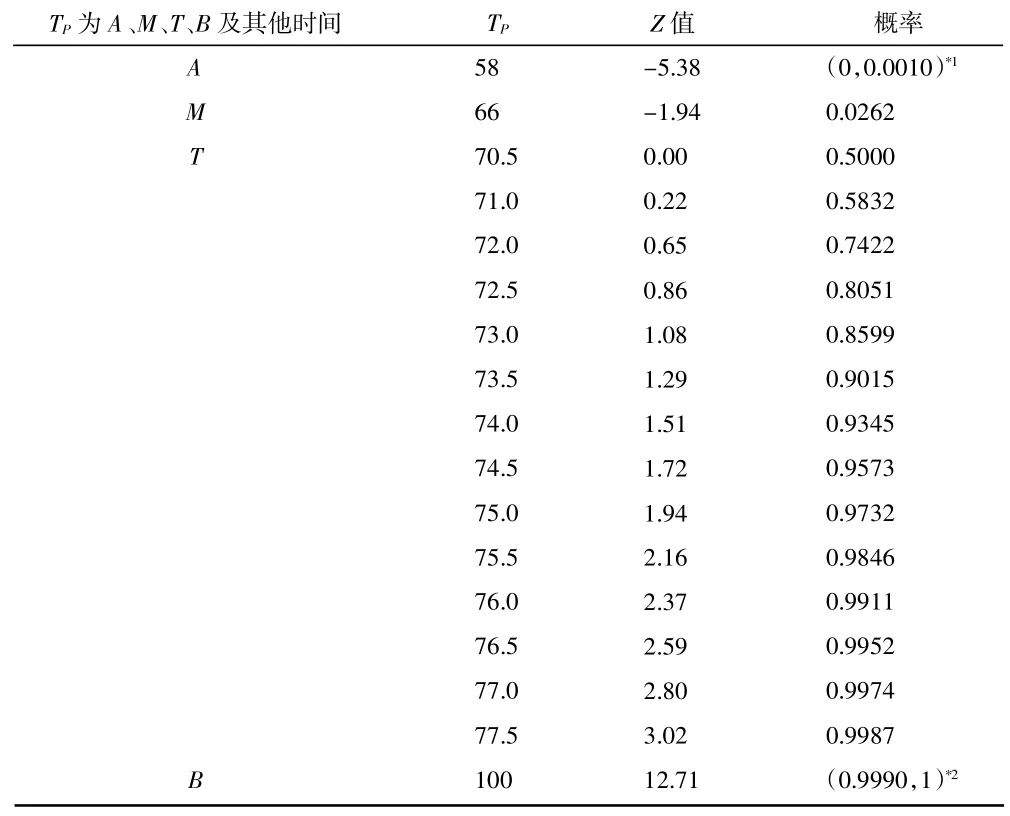
表5 工业遗产再利用的项目完成概率
表4 中可见TP=A=58 周的情况下,项目完成概率趋近于0;TP=M=66 周的情况下,项目完成概率为0.026 2;TP=B=100 周的情况下,项目完成概率趋近于1。虽然100 周的情况下,完成项目的概率趋近于1,但是用100 周来制定项目的计划完成时间,时间计划会过于宽松。因此,需要在TP为70.5 周~100周之间,找出完成项目概率在0.9 以上的相应时间。表4 可见,在74.5 周完成项目的概率为0.957 3,在77.5 周完成项目的概率为0.998 7。
四、结语
本文使用关键路径分析法,对工业遗产再利用做一探索性的研究。通过项目网络图的构建和CPM分析,得知工业遗产再利用的关键路径为:项目策划—项目建议书——设计任务书—规划设计——设计方案——建筑施工图——选择承包商—建筑施工——工程验收—客户进入——二次装修,这一条关键路径的总体期望完成时间为70.5 周。该项目为不确定活动时间的情况,通过概率计算,在74.5周左右时间内完成整个项目的开发工作的概率为0.95。由此可见,使用关键路径分析法,能够让项目管理者更好的调控监督工业遗产再利用开发的进程,为项目的顺利交付使用提供有力保障。
