双系统估计量与人口普查内容误差评估

胡桂华,漆 莉,迟璐婕

(重庆工商大学 a.数学与统计学院;b.长江上游经济研究中心,重庆 400067)

一、引 言

每次人口普查之后,都要进行质量评估调查,评估其登记质量。质量评估调查为抽样调查,抽样单位为范围较小的地理区域,如中国的普查小区(平均含住房单元80个),美国的街区群(平均含住房单元31.5个),南非的普查计数区(平均含住房单元140个)[1-2]。质量评估调查通常采取分层抽样或分层多重抽样。中国、南非和乌干达等发展中国家大多采取分层抽样,而美国、瑞士和英国等发达国家采取分层多重抽样。

人口普查质量评估包括覆盖误差评估和内容误差评估[3]。这两项评估应该同步进行,使用同一样本资料。覆盖误差指目标人口总体的实际人口数与普查登记人口数之差。内容误差指各种统计分组的各组实际人口数与其普查登记人口数之差。

从人口普查质量评估工作的完整性及必要性来看,不只是要评估覆盖误差,还要评估内容误差,然而内容误差评估尚处于起步阶段。扩大内容误差评估在各国开展,创新内容误差评估理论已成为当今人口普查质量评估领域需要迫切解决的国际前沿问题。

本研究目标是使用提出的“完整测度的内容误差估计量”替代联合国统计司建议各国使用的比率内容误差估计量。“完整测度的内容误差估计量”的构建分为三个步骤:第一步是对每一种统计分组(如按照性别分组),计算各组(男性组或女性组)的实际人口数与普查登记人口数之差。第二步是计算各个组的相对权数。第三步是计算该种统计分组的加权算术平均数。不难看出,由于各个组的普查登记人口数已知,所以“完整测度的内容误差估计量”构造关键是建立估计各个组实际人口数的估计量。例如,对普查登记人口数按照性别分组,共分为两组,即男性组和女性组。男性组普查登记人口数为600人,女性组普查登记人口数为400人,男性组和女性组各自占比分别为60%和40%。使用双系统估计量估计的男性组人口数为605人,女性组人口数为403人。男性组和女性组各自的内容误差分别为5人和3人。按性别分组的综合内容误差为5×0.6+3×0.4=4.2人。

各组实际人口数所用的估计量,应该与计算人口普查覆盖误差时所采用的估计量相同。如果在那里使用双系统估计量,则在这里也应该使用双系统估计量;如果在那里使用三系统估计量,则在这里也应该使用三系统估计量。这样做的理由是,在人口普查覆盖误差中构造目标人口总体实际人口数的双系统或三系统估计量时,需要选择若干个与人口登记概率相关的人口变量,对人口进行复合分组,把登记概率不同的人口分开,而把登记概率相同的人口分在同一个组内(简称为对人口的等概率分层),之后分别在各个等概率层内构造双系统或三系统估计量。有了这一工作基础,在内容误差测度中,如果对某个组进行等概率分层的若干变量与用于覆盖误差估计的那些分层变量恰好相同,那么用于计算各组实际人口数的双系统或三系统估计量便可由有关等概率层的计算结果合并得到。

本文采取双系统估计量估计各个组的实际人口数。一方面,相比只依据质量评估调查人口名单构造的单系统估计量,依据这份名单和普查人口名单构造的双系统估计量覆盖人口总体的范围更广,估计的各组人口数更接近于实际人口数;另一方面,虽然依据这两份名单和行政记录人口名单构造的三系统估计量覆盖总体人口的范围最大,但其结构和计算比双系统估计量要复杂许多。另外,迄今所有国家在覆盖误差估计中仍然使用双系统估计量。

本研究创新体现在三个方面:第一,提出基于双系统估计量的“完整测度的内容误差估计量”。第二,提出覆盖普查项目填写错误、普查多报与漏报的“完整测度的内容误差估计量”,从而把产生所有源头的内容误差全部置于测度的视线之内,将内容误差估计引入正确方向,为内容误差估计精度提供了理论保障。第三,利用同一套样本数据计算净覆盖误差及内容误差,实现覆盖误差与内容误差同步计算的工作目标。通过查阅国内外相关文献资料,尚未见到政府统计部门或其他学者做这样的研究。

研究的实际意义为:“完整测度的内容误差估计量”解决了比率内容误差估计量未包括普查多报与漏报引起的内容误差,从而低估总体内容误差的问题。研究的理论意义或学术价值为:“完整测度的内容误差估计量”属于复杂估计量,其构成元素也是估计量,抽样方差采取分层刀切抽样方差估计量近似计算。估计各组人口实际人口数的双系统估计量须在等概率人口层建立,否则产生异质性偏差,影响估计精度。各组人口在普查中的登记概率不相同,需要选择与登记概率相关的变量对其分层。

研究应用前景广阔。中国是人口大国,国民经济发展迫切需要解决的关键问题是人口数目的准确性问题。人口普查是中国和其他国家获得人口数的基本方法。各国普查后发布各组普查人口数,社会公众关注各组普查登记人口数是否正确。内容误差评估应向社会公众提供各组实际人口数与各组普查登记人口数的差异,为其决定是否使用及在多大程度上使用各组普查人口数提供依据。作者长期与中国国家统计局合作开展人口普查质量评估研究,为中国制订了2020年人口普查质量评估方案。国家统计局对该方案的评审意见是:借鉴了当今国际人口普查质量评估领域的前沿研究成果;吸纳了中国1982年、1990年、2000年和2010年人口普查及其事后质量抽查方案的成功之处;针对实际工作中的若干难点问题提出了创新性的应对策略;整个方案具有科学性、合理性和可操作性。因此,本研究希望应用于中国和其他一些国家未来的内容误差评估和其他相关领域。

二、文献综述

在人口普查质量评估中,美国、加拿大、英国、瑞士等发达国家只评估覆盖误差,而未评估内容误差[4]。中国、南非和卢旺达等发展中国家则同时评估覆盖误差和内容误差。这与各国人口普查质量评估的传统,以及对内容误差评估的重视程度和普查项目的登记质量有关。美国自1790年第一次人口普查起,每次只评估覆盖误差。中国自1982年第三次人口普查起,每次评估内容误差。

人口统计分析模型虽然提供不同性别、不同年龄、不同种族的人口数,但它未计算统计分组的整体误差,而且对总体人口进行的统计分组仅仅局限在性别、种族和年龄,因而不属于内容误差评估,而属于覆盖误差评估范畴。美国等发达国家及联合国统计司一直把它当作覆盖误差评估方法。发展中国家的内容误差评估方案也未提及人口统计分析模型。

在覆盖误差评估中,许多国家把覆盖误差(总体实际人口数与总体普查人口数之差)作为评估的主要目标。目前主要使用双系统估计量估计总体实际人口数,未来可能用三系统估计量取代双系统估计量[5-6]。

在内容误差评估中,最具代表性的成果是联合国统计司组织美国、英国和新西兰等国的人口普查质量评估专家撰写的“质量评估调查操作指南”,该指南简要介绍了比率内容误差估计量,建议各国使用它。该估计量有五种形式,即未加权净差异率、未加权不一致性指数、未加权总不一致性指数、未加权一致性率和未加权总差异率[7]。

比率内容误差估计量存在三个严重缺陷。第一,它的构成元素是样本的未加权数据,未将样本指标通过抽样权数扩张到总体,构造总体的内容误差比率估计量[8-10]。这是一个理论失误。第二,它只测度普查项目填写错误引起的内容误差,而未包括普查多报与漏报引起的内容误差,从而低估总体内容误差。该估计量需要同一人在普查与质量评估调查中对同一普查项目提供的答复。这不得不将评估对象局限在同时登记在这两项调查的匹配人口。普查多报人口不会登记在质量评估调查中,而普查漏报人口不会登记在普查中,因此多报和漏报人口不可能成为匹配人口。在匹配人口中观察内容误差,势必遗漏多报和漏报引起的内容误差。第三,它采取比率形式,无法看出各组实际人口数与普查登记人口数差异。对普查数据用户来说,他们很想知晓这个差异。“完整测度的内容误差估计量”能够弥补比率内容误差估计量的这三个缺陷[11]。

截至2020年,发展中国家一直使用比率内容误差估计量评估内容误差。中国1982年使用未加权一致性率估计年龄、性别、与户主关系、常住人口户口登记状况、出生人口和死亡人口差错率,1990年、2000年和2010年使用未加权一致性率估计年龄和性别差错率[12]。南非于2011年使用未加权净差异率、未加权不一致性指数等估计性别、年龄、婚姻状况、受教育程度和与户主关系的误差率[13]。中国和南非的内容误差评估除存在比率内容误差估计量的缺陷外,还存在另外的缺陷,即评估的统计分组过少。为了全方位反映普查的登记质量,应将内容误差的评估由目前的年龄、性别、婚姻状况、与户主关系、文化程度,逐步扩大到所有容易发生登记误差的统计分组。每一个统计分组,对应一个普查项目。例如,性别是一个普查项目,在普查表中填写男性和女性。普查登记工作结束后,按照性别分组,计算男性普查登记人口数和女性普查登记人口数,使用双系统估计量估计男性组和女性组的实际人口数,估计各个组的内容误差及综合内容误差(率)。

既然比率内容误差估计量存在严重缺陷,那发展中国家为什么迄今还使用它呢?原因为:第一,发展中国家并未意识到这些缺陷。未意识到源于不重视内容误差评估。如果对内容误差评估和覆盖误差评估给予同样的重视程度,内容误差评估理论不至于像目前这样严重滞后于覆盖误差评估。第二,该估计量计算方便,直接依据样本数据估计内容误差,无需考虑抽样方法和抽样权数等复杂理论问题。如果考虑抽样权数,就需要使用权数构造每个样本小区普查项目答复各组人口数的线性估计量,然后汇总,计算量大,尤其是在复杂抽样情况下。第三,确定抽样权数要考虑很多因素。例如,普查小区总数及样本小区数(也可以是住房单元数或人口数)、抽样方法、住房单元或个人答复率。

从以上研究意义的分析,以及对国内外研究现状的评述可以看出,比率内容误差估计量存在诸多缺陷。本文所提出的“完整测度的内容误差估计量”能避免这些缺陷。可以预见,在未来内容误差评估中,用“完整测度的内容误差估计量”取代比率内容误差估计量是必然趋势。

三、双系统估计量及其抽样方差估计量

构造和使用双系统估计量的目的是,估计“完整测度的内容误差估计量”各个组的实际人口数。如同其他任何统计模型一样,双系统估计量也是建立在一些假设条件的基础上。如果这些假设条件不成立,或者部分假设条件不成立,就不能使用双系统估计量,或者使用双系统估计量估计的人口数精度低[14-16]。

双系统估计量建立在五个假设条件基础上。第一,独立性假设。该假设说的是,总体中的人是否在普查中登记,不影响到他们是否在质量评估调查中登记。独立性假设失败源于普查与质量评估调查的相关性,即包括在普查中使得人们更可能或更不可能包括在质量评估调查中,使双系统估计量系统性地高于或低于实际人口数,另外还源于等概率人口层的人在普查与质量评估调查中登记概率的异质性。这种异质性通常表现为,在普查登记中的人会更可能在质量评估调查中登记,使得双系统估计量系统性地低估实际人口数。第二,总体封闭假设,即在普查和质量评估调查时,总体规模不变。第三,无比对误差,即比对普查和质量评估调查时,不会发生比对误差。第四,在普查和质量评估调查中不会登记目标普查总体之外的人。第五,总体中的人有同样的概率在普查中登记,也有同样的概率在质量评估调查中登记,但不要求这两个登记概率相同。

(一)双系统估计量的建立

用N表示某个总体或某个组的人口规模,使用双系统估计量估计它。双系统估计量的英文单词是Dual System Estimator,缩写为DSE。用i表示总体中的任意一个人,i=1,2,3,…,N。用pijk表示第i人在普查(用j表示)和质量评估调查(用k表示)的登记概率,j=1,2,k=1,2。j=1,2分别表示总体中的人在普查中登记或未在该调查中登记。k=1,2分别表示总体中的人在质量评估调查中登记或未在该调查中登记。如果总体中的人口在这两项调查的登记概率相等,那么pi11/pi12=pi21/pi22,或者pijk=pij+pi+k;如果两项调查相互独立,那么pi1+=p1+,pi+1=p+1;另外两项调查是对总体的全面登记。在这三个假设条件同时满足的情况下,双系统估计量的似然函数为:

(1)

式(1)的最大似然估计量为:

(2)

其中,N1+为正确普查登记人口数,N1+=N11+N12,而N+1、N11、N12、N21、N22分别表示在质量评估调查中登记的人口数、同时登记在普查和质量评估调查人口数、在普查中登记但未在质量评估调查登记人口、在质量评估调查登记但未在普查中登记人口数、同时未在两项调查中登记人口数。质量评估调查人口数N+1=N11+N21。p1+和p+1分别表示总体中的人口在普查和质量评估调查中的登记概率。用DSE替代N,得到式(3):

(3)

人口普查登记工作结束之后,得到的普查登记人口总数C中除包括正确普查登记人口数CE,错误普查登记人口数EE,估算的普查人口数II,直到质量评估调查比对时仍然未送到质量评估调查办公室的普查人口数LA。

N1+=C-II-LA-EE

(4)

引入普查数据定义人口数DD,即在普查中登记了姓名和至少一个人口统计特征的人口数,它定义为:

DD=C-II-LA

(5)

从式(4)和式(5)可以看出,

N1+=C-II-LA-EE=DD-EE=CE

(6)

普查错误登记的数目通常采取式(7)估计:

(7)

其中,CE=根据E样本估计的普查正确登记人口数,NE=根据E样本估计的普查登记人口数。然而,通常期望E样本的加权人口数的数学期望等于普查数据定义人口数,即E(NE)=DD,此时:

(8)

如果普查登记中没有普查错误登记人口数EE,那么式(4)变为式(9):

N1+=C-II-LA

(9)

如果普查登记中没有估算的普查登记人口数II和直到质量评估调查比对时仍然未送到质量评估调查办公室的普查人口数LA,那么式(4)变为式(10):

N1+=C-EE

(10)

如果普查登记中没有普查错误登记人口数EE,直到质量评估调查比对时仍然未送到质量评估调查办公室的普查人口数LA,那么式(4)变为式(11):

N1+=C-II

(11)

从式(4)和式(9)～式(11)可以看出,在不考虑质量评估调查与普查之间人口移动的情况下,双系统估计量共有4种形式,现分别写出如下:

(12)

(13)

(14)

(15)

为节省篇幅,同时不失一般性,对式(12)做进一步讨论。在普查日与质量评估调查日之间不可避免发生人口移动。有些人从其他小区迁移到本样本普查小区(称为向内移动人口),也有些人从本样本小区迁移到其他小区(称为向外移动人口),还有些人普查日和质量评估调查日均居住在本样本小区(称为无移动人口)。质量评估调查人口数有两种构造方式:一是无移动人口数Nnon-movers和向内移动人口数Nin-movers之和;二是无移动人口数Nnon-movers和向外移动人口数Nout-movers之和。相应地质量评估调查与普查的匹配人口数也有两种形式:一是无移动匹配人口数Mnon-movers和向内移动匹配人口数Min-movers之和;二是无移动匹配人口数Mnon-movers和向外移动匹配人口数Mout-movers之和。用公式表示如下:

N+1=Nnon-movers+Nin-movers或者N+1=Nnon-movers+Nout-movers

(16)

N11=Mnon-movers+Min-movers或者N11=Mnon-movers+Mout-movers

(17)

将式(16)、式(17)代入式(12),分别得到式(18)、式(19):

(18)

(19)

在质量评估调查中,由于找到本样本小区的向外移动人口很困难,而找到向内移动人口很容易,因此式(18)具有实用性,而式(19)只具有理论意义。本着科学研究服务于应用的原则,对式(18)做进一步研究。

式(18)成立的前提条件是,质量评估调查是对总体的全面调查。包括美国、瑞士等国在内的政府统计部门都是在这一前提条件下讨论双系统估计量的。这一条件虽然在现实中不成立,但在理论上是可能实现的。事实上,只要有足够经费和时间,质量评估调查完全可以像普查那样对总体人口全面登记。考虑到质量评估调查实际上是对总体的抽样登记,即只是调查全国所有普查小区的一部分小区,故式(18)中除了C,II,LA已知外,其他构成元素一律要用样本数据来估计,用符号“Λ”表示,此时式(18)变为式(20)。由于式(20)只能在等概率人口层v计算,故将式(20)写为:

(20)

(21)

其中,在每层采取简单随机抽样下,whi=Nh/nh。

(二)双系统估计量的抽样方差

式(20)是一个很复杂的估计量,没有精确计算其抽样方差的公式,故使用分层刀切法近似计算双系统估计量的抽样方差[17-20]。对分层刀切法,关键的是计算复制权数。当层g的t样本单位剔除后,层h的i样本单位的复制权数whi(gt)为:

(22)

(23)

进而写出式(20)的复制估计量为:

(24)

(25)

(26)

(27)

(28)

如果ng=1,那么:

(ng-1)/ng=1

(29)

四、内容误差估计量及其抽样方差估计量

(30)

(31)

(32)

(33)

(34)

(35)

(36)

(37)

式(30)～式(37)中的Ct为第t组的普查登记人口数,为已知数。实际上,第t组的普查登记人口数也可以使用样本普查小区的普查人口名单构造的单系统估计量来估计。联合国统计司建议各国政府统计部门在覆盖误差和内容误差估计中使用估计的普查登记人数。

五、实证分析

(一)基本情况

为便于读者理解和运用式(1)～式(37),进行实证分析是必要的。中国《人口普查条例》规定,普查及其质量评估调查所得到的微观住户及个人数据属于保密数据。除国家统计局及国内少数高校外,其他单位和个人难以获得。即使在签订了数据使用保密协议的情况下,使用者也无法将人口普查微观数据储存在自己的电脑中,随时提取使用。

美国明尼苏达大学人口研究中心拥有世界上一些国家的人口普查微观数据。从1995到2017年年底,该中心建立的IPUMS数据库收集了中国、美国、白俄罗斯、印度、英国等85个国家的政府统计部门的约6亿7 700万人在301次人口普查中的微观个人记录。这些微观记录包括普查员收集的住户及个人的人口统计特征变量及其变量值。美国普查局不只是免费提供给IPUMS数据库历次人口普查微观记录,还免费提供美国1990年、2000年和2010年质量评估调查人口名单。这就是从IPUMS数据库获取实证分析数据的原因。

本文从IPUMS数据库获得了2010年美国明尼苏达州的质量评估调查10个样本街区群的普查人口名单及其质量评估调查人口名单。这10个样本街区群来源于该州大型街区群层,用h=1表示,每个街区群含住房单元80个及以上;中型街区群层用h=2表示,每个街区群含住房单元3～79个;小型街区群层用h=3表示,每个街区群含住房单元0～2个。另外还获得了各种族组、各年龄组、各性别组和房屋所有权的普查登记人口数、后期加入的普查人口数、估算的普查人口数等。为获得双系统估计量所需要的匹配人口数,比对普查名单及其质量评估调查名单。比对的内容包括姓名、性别、年龄、文化程度、房屋所有权、居住位置、婚姻状况、国籍、种族。对初次比对结果为未匹配人口和可能的匹配人口,组织后续调查,利用收集的新信息再次比对,见表1和表2。

表1 样本及未加权人口数

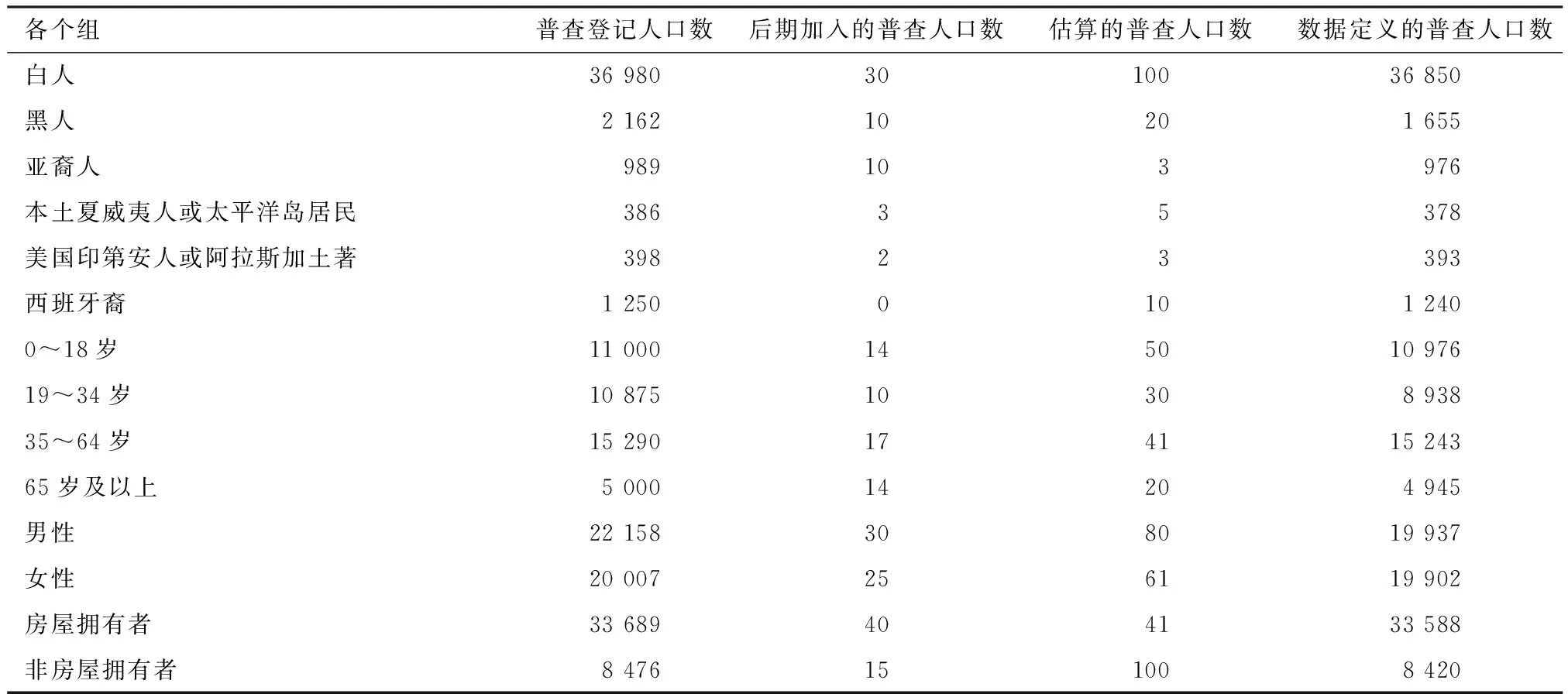
表2 各组人口的已知普查人口数

为估计各组人口的实际人口数,需要对各组人口等概率分层。例如,对于组“白人”按照房屋所有权、性别和年龄分层,总共分为16层。在这16层中的每一层使用双系统估计量估计实际人口数。汇总16层估计的实际人口数,得到组“白人”的实际人口数估计值。分层结果如表3。

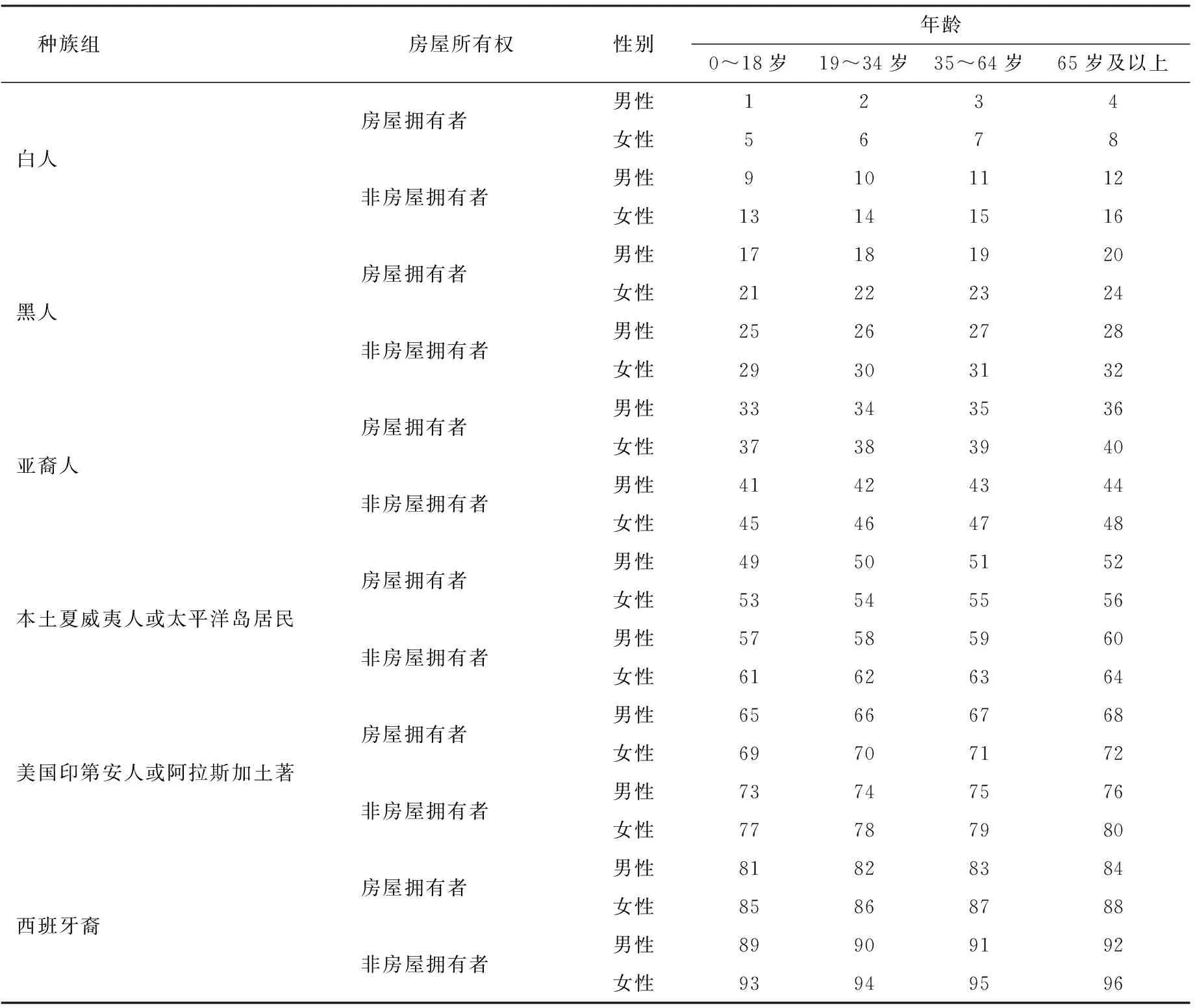
表3 各组人口的等概率分层

很显然,如果分层变量过多,总的层数就越多。在样本规模一定情况下,每一层估计的实际人口数的抽样方差就越大。分层变量也不能太少。过少的分层变量使得每个等概率人口层的异质性增大,导致异质性偏差。因此,在决定选择多少个变量对各个组分层时,既要控制抽样方差,也要减少异质性偏差。

为了解决抽样方差和异质性偏差不能同时减少的问题,美国普查局在2010年构造基于Logistic回归模型的双系统估计量。其基本思路是,把所有分层变量当作Logistic回归模型的自变量,将普查正确计数概率等当作该模型的因变量,以此完成对总体人口等概率分层构造双系统估计量的任务。由于回归分析中回归自变量的数目不受限制,所以分层变量受样本规模限制的问题得到了解决。

美国普查局在2010年同时使用基于对总体人口直接等概率分层的双系统估计量和基于Logistic回归模型双系统估计量估计总体实际人口数。结果发现后者比前者估计精度提高较少,而且基于Logistic回归模型双系统估计量很复杂,不便于操作与应用。于是2010年后,美国普查局决定放弃使用Logistic回归模型双系统估计量,仍然使用基于对总体人口直接等概率分层的双系统估计量。

从表3可以看出:(1)各组人口是对总体人口进行一次等概率分层的结果;(2)各组人口等概率分层的对象是各组人口本身,而不是总体人口,是对各组人口进一步的分层;(3)每个等概率人口层是4个变量交叉分层的结果;(4)估计的各组人口“白人”的双系统估计值为1～16这16个等概率人口层使用双系统估计量估计的实际人口数之和;(5)估计的各组人口“黑人”的双系统估计值为17～32这16个等概率人口层使用双系统估计量估计的实际人口数之和;(6)估计的各组人口“亚裔人”的双系统估计值为33～48这16个等概率人口层使用双系统估计量估计的实际人口数之和;(7)估计的各组人口“本土夏威夷人或太平洋岛居民”的双系统估计值为49～64这16个等概率人口层使用双系统估计量估计的实际人口数之和;(8)估计的各组人口“美国印第安人或阿拉斯加土著”的双系统估计值为65～80这16个等概率人口层使用双系统估计量估计的实际人口数之和;(9)估计的各组人口“拉美裔者”的双系统估计值为81～96这16个等概率人口层使用双系统估计量估计的实际人口数之和;(10)仿照此思路可以分别得到“0～18岁”“19～34岁”“35～64岁”“65岁及以上”各组人口的实际人口数估计值、拥有房屋者和非房屋拥有者的实际人口数估计值,以及男性和女性的实际人口数估计值。

(二)估计结果与分析

使用表1和表2数据,以及式(20)、式(21)计算表3每个等概率人口层的双系统估计值,然后相加,得到各组人口的实际双系统估计值。在此基础上,使用式(34)和式(36)估计各组人口的覆盖误差、覆盖误差率,以及内容误差、内容误差率,估计结果如表4。

表4 估计的各组人口的人口数及内容误差

为了说明表4中的各个统计分组的“估计的综合内容误差”及“估计的综合内容误差率”是如何由式(34)和式(36)得到的,以统计性别分组为例说明,“估计的综合内容误差”及“估计的综合内容误差率”分别为:

279=[22 158×(-1 147)+20 007×1 859]/[22 158+20 007]

0.02=[22 158×(-0.05)+20 007×0.09]/[22 158+20 007]

由表4可知:(1)按照种族分组,“黑人”组的内容误差率最大,为-0.28,而“白人”组的内容误差率最小,为0.02;按照年龄分组,“65岁及以上”组的内容误差率最小,为0.03;按照性别分组,“男性”组的内容误差率-0.05小于“女性”的内容误差率0.09;按照房屋所有权分组,“非房屋拥有者”组的内容误差率小于“房屋拥有者”组。(2)从绝对数来看,按照种族分组的综合内容误差最大,为642人,而按照年龄分组的综合内容误差最小,为270人。从相对数来看,按照种族分组和年龄分组的综合内容误差率均为0.01,而按照性别和房屋所有权分组的综合内容误差率均为0.02。

在计算了内容误差之后,再来计算其抽样方差。根据抽样方差判断内容误差估计值的精度,首先使用表1数据和式(22)得到样本街区群的复制权数,计算结果见表5。

表5 样本普查小区复制权数的计算结果

由表5可知:(1)刀切某一样本街区群后所计算的10个样本街区群的复制权数的总和,等于原来的10个抽样权数的总和;(2)刀切某一样本街区群后使得样本街区群之间的抽样权数发生变化;(3)每切掉一个样本街区群都要重新计算一次抽样权数,有多少个样本街区群就要刀切多少次。

使用式(22)～式(33)和表1～表5中数据,得到每种分组的内容误差及内容误差率的抽样标准误差,以及各个组的覆盖误差及覆盖误差率的抽样标准误差,见表6。

从表6可以看出:(1)为消除规模效应影响,最好使用相对数,而不是绝对数来说明问题。对表6来说,使用内容误差率说明估计精度高低更为合适。(2)从综合内容误差来看,按年龄分组的综合内容误差率的抽样标准误差最大,为0.61,而按照性别或房屋所有分组的综合内容误差率的抽样标准误差最低,为0.03,按照种族分组的综合内容误差率的抽样标准误差中等,为0.06。这表明,按照性别或房屋所有分组的内容误差率的估计精度最高,而按照年龄分组的内容误差率的估计精度最低。(3)从各组内容误差来看,在按种族分组的情况下,“白人”组和“本土夏威夷人或太平洋岛居民”组的内容误差率的抽样标准误差最低,均为0.04,估计精度最高,而“拉美血统者”组的内容误差率的抽样标准误差最大,为0.71,估计精度最低;在按照年龄分组情况下,“65岁及以上”组的内容误差率的抽样标准误差最大。在按照性别分组情况下,“男性”组和“女性”组的内容误差率的抽样标准误差一样,估计精度几乎持平。在按照房屋所有权分组情况下,“房屋拥有者”组和“非房屋拥有者”组的内容误差率的抽样标准误差一样,估计精度几乎持平。

六、结 论

联合国统计司的比率内容误差估计量是目前发展中国家评估内容误差的唯一方法。该方法存在三个严重缺陷,即评估的是样本本身的内容误差;未包括普查多报与漏报引起的内容误差;采取比率形式无法看出各组实际人口数与普查登记人口数差异。“完整测度的内容误差估计量”能避免这些缺陷,将在未来人口普查内容误差估计中发挥作用。

构造“完整测度的内容误差估计量”的关键是建立估计各组实际人口数的估计量。根据资料的可得性,充当各组人口实际人口数的估计量可能是单系统估计量、双系统估计量和三系统估计量。目前使用双系统估计量是恰当的。

为构造估计各组人口实际人口数的双系统估计量,需要解决三个问题。第一,对各组人口进行等概率分层。首先把影响各组人口在普查和质量评估调查中登记概率的变量找出来,形成不重复变量群,然后根据样本规模选择分层变量。如果样本规模足够大,就把变量群中的所有变量作为分层变量。如果样本规模未达到足够大,就使用加权优比排序法计算各个变量与“在普查中是否登记变量”的优比,根据优比值选择重要分层变量。如果样本规模过小,就把变量群的所有变量作为Logistic回归模型的自变量,把普查正确登记概率和匹配概率作为模型的因变量,利用Logistic回归模型预测的正确登记概率和匹配概率构造基于Logistic回归模型的双系统估计量。第二,获得普查人口名单及质量评估调查人口名单的匹配人口。这需要比对普查人口名单及质量评估调查人口名单。匹配人口指同时登记在两份名单的人口。如果同一人在两份名单的姓名、年龄、文化程度、房屋所有权、种族或民族、居住地这些特征全部或大部分相同,就作为匹配人口。如果比对信息不足,就组织后续调查,收集新信息再次比对。再次比对后,对依然无法确认比对结果的悬而未决者,依据匹配人口和未匹配人口数比例在匹配者和未匹配者之间分配。第三,双系统估计量构造复杂,无法用精确公式计算其抽样方差。其方差包括两个部分:一部分是用普查和质量评估调查全面资料构造双系统估计量时所产生的方差;另一部分是使用有限总体概率样本资料估计前者每个构成部分子总体指标产生的抽样方差。这两个部分的方差无法使用一个数学解析式表示,只好采用分层刀切抽样方差估计量近似计算。