线性工具变量模型中有效工具变量的识别研究
2021-08-30赵培信杨宜平
李 庆,赵培信,b,杨宜平
(重庆工商大学a.数学与统计学院;b.经济社会应用统计重庆市重点实验室,重庆 400067)
一、引 言
考虑如下线性回归模型:
Y=XTβ+ε
(1)
其中,β=(β1,β2,…,βp)T为p维未知的参数向量,X为协变量,Y为对应的响应变量,ε为零均值的模型误差。当X为外生协变量,即协变量X与模型误差ε相互独立时,基于普通最小二乘方法可以得到模型参数β的有效估计。但当X与ε存在较强的相关性,即X为内生协变量时,基于普通最小二乘方法对β估计将不再是相合的,而产生一定的内生性偏差。在X为内生协变量的情况下,基于工具变量调整技术则可以给出β一个相合估计。具体地,假定X为内生协变量,且满足:
X=ΓZ+e
(2)
其中,Z为q维工具变量,Γ为p×q维的未知参数矩阵,e为模型误差。
近年来,对基于工具变量调整的统计推断理论已有大量文献进行了研究。比如Cai等研究了部分变系数工具变量模型的估计问题,并提出了一种三阶段估计方法[1]。Zhao等研究了变系数工具变量模型的变量选择问题,并提出了一种基于光滑门限估计方程的变量选择方法[2]。Fan等则对高维的线性工具变量模型进行了研究,并提出了一种基于惩罚的广义矩(GMM)估计方法[3]。Chen等对部分线性工具变量模型,在由于协变量的内生性而导致过度识别的情况下,提出了一种基于广义矩(GMM)估计方法[4]。Yang等针对部分线性单指标工具变量模型的统计推断问题,提出了一种基于经验似然的估计方法[5]。Huang等则针对部分线性工具变量模型的变量选择问题,提出了一种基于正交加权的经验似然变量选择方法[6]。
基于工具变量的统计推断过程中,选取有效的工具变量是进行统计推断的关键,但是上述文献均是在假定已知有效工具变量的前提下,研究模型参数β的估计及变量选择等统计推断问题。而如何选取有效的工具变量并没有进行研究。关于有效工具变量的识别问题,近年来也越来越受到统计学界的关注。比如Lin等和Belloni等结合惩罚最小二乘方法研究了线性工具变量模型的正则估计问题,对模型中有效工具变量的识别问题提出了一种基于惩罚最小二乘的识别方法[7-8]。Chen等则对线性工具变量模型中有效工具变量的识别问题提出一种基于两阶段惩罚最小二乘方法的识别过程[9]。总体来看,目前研究有效工具变量识别的文献不是太多,而在实际的回归建模过程中往往需要从大量的指标中选取某些指标作为有效工具变量,因此对有效工具变量的识别成为内生协变量回归建模研究中一个重要的课题。基于此,本文在X为内生协变量,并且在线性模型结构(1)和(2)下,研究工具变量Z的识别问题。
本文通过构造一个辅助回归模型,并结合惩罚最小绝对偏差估计技术,对模型结构(1)和(2)中的有效工具变量给出了一种识别方法。数据模拟研究表明所提出的有效工具变量识别方法是行之有效的。本文提出的基于惩罚最小绝对偏差的识别方法允许工具变量的采集数据含有异常值。因此,与Lin等、Belloni等和Chen等所提出的基于惩罚最小二乘的有效工具变量识别方法相比[7-9],本文所提出的有效工具变量识别方法具有较好的稳健性。另外,与Chen等提出的基于两阶段惩罚最小二乘方法的有效工具变量识别过程相比[9],本文所提出的识别方法是通过构造一个辅助回归模型来给出基于惩罚的最小绝对偏差有效工具变量识别过程,将大大减少计算量和计算复杂度。
二、有效工具变量识别及模型估计过程
注意到X为内生协变量以及Z为对应的工具变量可知:
E(ε|X)≠0,E(ε|Z)=0
(3)
记Zk为工具变量Z=(Z1,Z2,…,Zq)T的第k个分量,那么结合式(1)和(3)可得:
(4)
由模型(2)可知,如果Zk为有效的工具变量,那么Zk与X有显著的线性相关关系。因此,如果对所有的j,1≤j≤p有Cov(Xj,Zk)=0,j=1,2,…,p,则Zk为无效的工具变量。进而由式(4)可知,如果Zk为无效的工具变量,则有Cov(Y,Zk)=0。定义如下辅助回归模型:
Y=θ1Z1+θ2Z2+…+θqZq+ε
(5)
那么由如上讨论可知,如果θk≠0,则可知Zk为有效的工具变量。因此,为了选择有效的工具变量,只需判断θ=(θ1,θ2,…,θq)T中的非零元素。为此,定义如下惩罚绝对偏差目标函数:
(6)
其中,pλ(·)为某一指定的惩罚函数。在实际应用中已有大量的惩罚函数可以应用,比如Lasso惩罚、SCAD惩罚以及MCP惩罚[10-12]等。
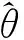
(7)
(8)
三、迭代计算
在这一部分,考虑工具变量识别以及模型参数估计方法的迭代计算问题。首先讨论最小化目标函数Q(θ)的计算方法。结合Zou等提出的线性逼近方法[13],式(6)中的惩罚函数pλ(|θk|)可以渐近表示为:
(9)

(10)
其中,ξk=(0,…,1,…,0)T为第k个元素为1,其他元素均为0的q维单位向量。那么式(10)可写为:
(11)
注意到式(11)为经典的最小一乘估计目标函数,因此可以通过已有的统计软件(如R软件、SPSS软件等)进行求解。另外在求解式(11)的过程中,调整参数λ需要指定,并且参数向量θ需要给出一个初始估计。首先,可以通过最小化如下不带惩罚项的绝对偏差目标函数来得到θ的一个初始估计:
(12)
另外,类似Wang等[14],本文建议用BIC准则对调整参数λ估计。具体地,通过最小化如下BIC准则函数来得到λ的估计。
(13)

第1步:最小化式(12)得初始估计量θ0。
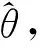
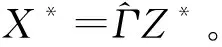

四、数值模拟研究
为实施模拟从如下模型产生数据:

(14)
其中,β=2,Γ=(2,1,0.5,0,…,0)为1×10维参数矩阵,对应的工具变量Zk~N(1,1.5),k=1,2,…,10。由Γ的前三个元素非零,其他元素均为零可知Z1、Z2和Z3为三个有效的工具变量,而Z4,Z5,…,Z10均为无效工具变量。响应变量Y以及内生协变量X均由模型产生,其中模型误差ε~N(0,0.5)并且e=0.5ε。该数据产生方法保证了E(Xε)≠0,即X为内生协变量。在模拟过程中,样本容量n分别取100、200和300三种情况,惩罚函数pλ(·)分别取Lasso惩罚、SCAD惩罚以及Adaptive-Lasso惩罚[10-11,15]三种情况。另外,为验证本文所提出方法的稳健性,对样本容量的每一种情况,对响应变量Y和内生协变量X人为设置部分异常点。在模拟过程中,考虑异常值占数据的5%和10%两种情况。对每一种情况,异常值通过模型误差取为ε~N(0,3)进行产生。
关于有效工具变量识别的模拟结果见表1和表2,其中“C”表示基于1 000次重复实验把真实无效工具变量正确估计为无效工具变量的平均个数,“I”表示基于1 000次重复实验把真实有效工具变量错误估计为无效工具变量的平均个数。另外,表1和表2还给出了选择有效工具变量的错误选择率(FSR),其定义为FSR=IN/TN,其中IN表示基于1 000次重复实验把无效工具变量估计为有效工具变量的平均个数,TN表示基于1 000次重复实验选择为有效工具变量的平均个数。由表1和表2,可以得到如下结论:

表1 异常值占5%时,基于不同惩罚函数选择有效工具变量的结果

表2 异常值占10%时,基于不同惩罚函数选择有效工具变量的结果
第一,随着样本量n的增加,基于三种惩罚方法的有效工具变量错误识别率均逐渐趋于0,并且对无效工具变量的识别也逐渐趋于无效工具变量的实际个数7。这表明本文提出的有效工具变量的选择方法是行之有效的。
第二,对任意给定的样本量n,在不同异常值数量下的模拟结果是类似的,即异常值对模拟结果没有明显的影响。这表明本文提出的工具变量选择方法具有较好的稳健性。
第三,当样本量较小时,基于Adaptive-Lasso和SCAD给出的模拟结果优于基于Lasso给出的模拟结果。但当样本量增大时,基于三种惩罚方法给出的模拟结果是类似的。
接下来模拟工具变量Z的维数变化对有效工具变量识别的影响。为此,取Γ=(2,1,0.5,0,…,0)为1×q维参数矩阵,并且在模拟过程中q分别取为q=15,20以及25三种情况。由Γ的定义可知Z1Z2和Z3为三个有效的工具变量,而其他q-3个均为无效工具变量。另外为了模拟本文所提方法的稳健性,模型误差取为厚尾的拉普拉斯分布ε~La(0,2)。其他数据的产生与模型(14)完全相同。在该模拟过程中,样本容量取为n=200,惩罚函数pλ(·)分别取SCAD惩罚、Lasso惩罚以及Adaptive-Lasso惩罚三种情况。模拟结果见表3。

表3 工具变量在不同维数下,有效工具变量的识别结果
由表3可以看出,在不同数量的无效工具变量下,模拟出来的错误选择率(FSR)是类似的,即无效工具变量的维数对模拟结果没有明显的影响。另外我们还可以看出在模型误差为厚尾分布的情况下,本文提出的有效工具变量识别方法仍可以给出较小的错误选择率(FSR),这也进一步表明本文提出的有效工具变量识别方法具有较好的稳健性。
接下来给出关于模型参数β的模拟结果。注意到无效工具变量的维数对有效工具变量的识别没有明显的影响,并且基于不同的惩罚函数识别出的有效工具变量差别不是太大。因此,在接下来的模拟过程中,假定工具变量的维数q=10,并用Lasso惩罚选择有效工具变量。其他情况下的模拟结果是类似的,为此不再重复展示。另外作为比较,还给出了关于β的朴素(naive)估计结果,即不经过工具变量调整,直接利用内生协变量X并通过最小化如下目标函数Qnaive(β)来得到β的估计。

图1 异常值占5%时,模型参数β估计量绝对偏差的箱线图
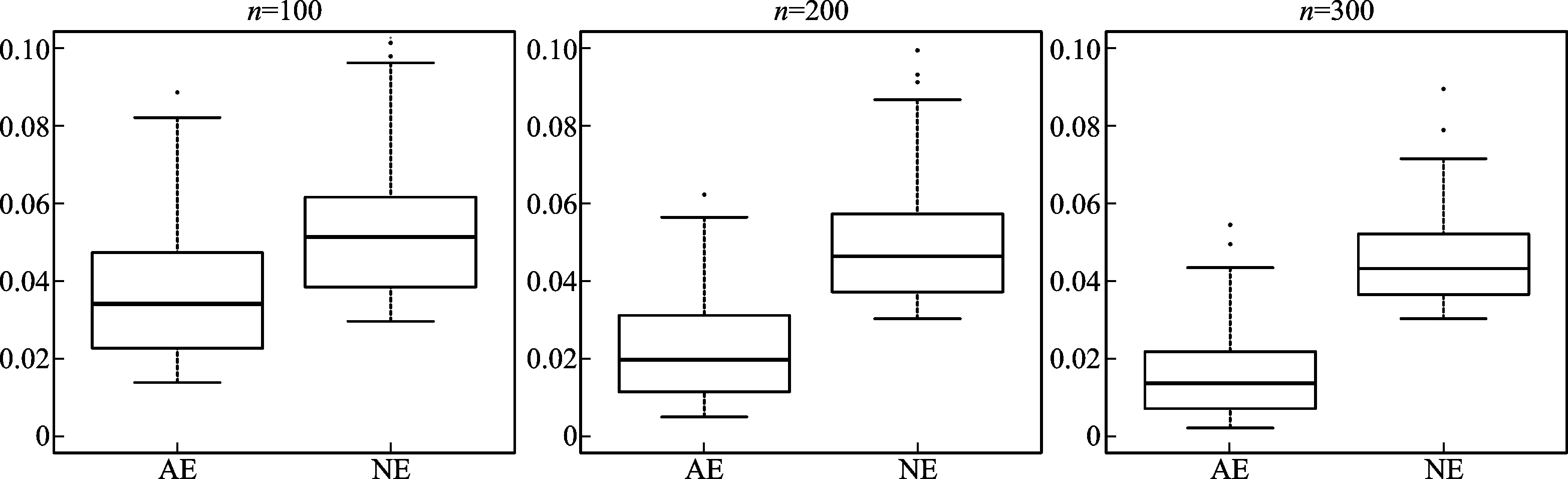
图2 异常值占10%时,模型参数β估计量绝对偏差的箱线图
五、实际案例分析
自从实施改革开放政策以来,中国的对外贸易呈现高速增长,经济得到了长足的发展,对外贸易开放不论在量上还是在质上也都有了巨大的飞跃。近年来,“一带一路”倡议的纵深发展进一步大幅度地推动了中国与沿线国家之间的双边贸易和投资。对外贸易开放在中国经济增长和高质量发展中的地位和作用也越来越受到大量学者关注。注意到对外贸易开放与经济增长是相互促进的,即把对外贸易开放作为因素变量,研究其对中国经济增长影响的时候,对外贸易开放是一个内生协变量。因此,我们用本文提出的工具变量模型估计方法研究中国对外贸易开放与经济增长之间的关系。
具体地,本文基于中国31个省份2009—2018年的相关数据,对贸易开放度与中国经济增长的关系进行实证分析研究。本文所涉及的数据均来自国家统计局网站《中国统计年鉴》。首先,参考已有文献,对各变量的设定和对应数据的计算方法进行简单说明。响应变量Y:采用以2009年为基期,各省份的实际GDP来代表各省份的经济发展水平。协变量X:采用各省份的进出口总额与该地区生产总值的比值来衡量各省份的对外贸易开放度。另外从就业、教育、地理位置三个方面选择三个指标作为工具变量。具体地,Z1表示各省份与国外市场的接近度,类似陈生明等[16],其计算方法为各省份省会城市到海岸线距离的倒数(乘100倍)乘以人民币对美元的名义汇率;Z2表示各省份的年底从业人员数;Z3表示各省份的人力资本存量,其用各省6岁及以上人口的平均受教育年限来衡量。因此,可建立模型为:
在接下来的模拟过程中,惩罚函数仍考虑SCAD惩罚、Lasso惩罚以及Adaptive-Lasso惩罚三种情况,并对所有数据进行自然对数变换。关于有效工具变量识别的模拟结果见表4。从表4可以看出,基于三种处罚方法给出的模拟结果是非常类似的,这也进一步验证了上一节数值模拟得出结论。并且从系数γ1的估计值不为零,而系数γ2和γ3的估计值均为零可知“Z1:国外市场接近度”为识别出的有效工具变量,而“Z2:从业人员数”和“Z3:人力资本存量”则为无效工具变量。另外,对回归系数β0和β1的估计,同时给出基于工具变量调整的估计(AE)以及未经过工具变量调整的朴素估计(NE),具体模拟结果见表5。由表5可以看出,对β1的估计,基于工具变量调整给出的估计值大于未经过工具变量调整的估计值。这就表明对外贸易开放度对当地的经济增长存在显著的正影响效应,并且如果忽略对外贸易开放度的内生性,则会低估对外贸易开放度在经济增长中发挥的作用。
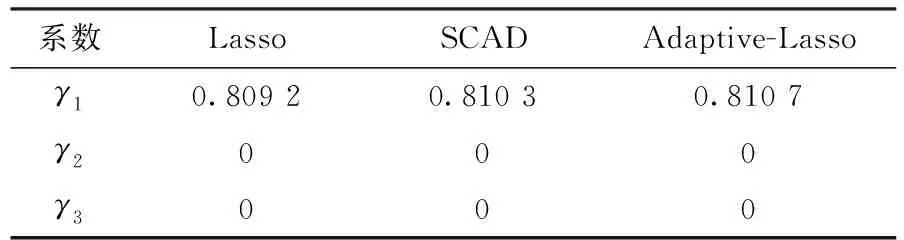
表4 基于不同惩罚方法系数γ1-γ3的估计结果
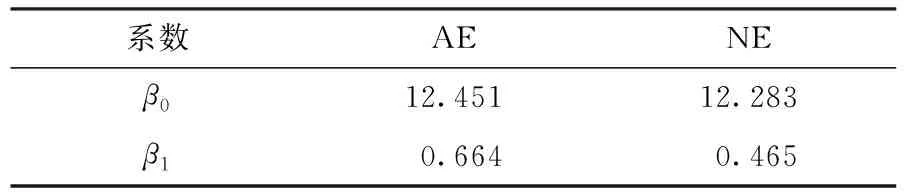
表5 回归系数β0和β1的估计结果
六、结论及建议
在对内生性数据进行统计推断过程中,如何选取有效的工具变量对内生性数据进行调整是对模型进行有效估计的关键一步。本文通过构造一个辅助回归模型并结合惩罚估计技术提出了一种有效工具变量识别方法。数据模拟研究表明所提出的有效工具变量识别方法是行之有效的,并具有较好的稳健性。
基于所提出的统计推断方法,本文对中国31个省份对外贸易开放度与经济增长的关系进行实证分析。研究结果表明在处理贸易开放度的内生性问题上,各地区的国外市场接近度是一个行之有效的工具变量,并且发现对外贸易开放对经济增长有着显著的推动作用。目前,中国正处在改革开放的攻坚期和深水区,全球性市场、技术和资源等要素的竞争日趋激烈。因此,在“一带一路”的倡议下,各省、自治区和直辖市需要全方位、宽领域地实行对外贸易的开放,积极地推进对外贸易的发展。
目前,半参数工具变量模型已被广泛应用到环境、经济以及生物医学等各个领域,但是本文在线性工具变量模型结构下讨论了有效工具变量的识别问题,所提出的识别方法不能直接应用于半参数工具变量模型的有效工具变量识别中。因此,半参数工具变量模型的有效工具变量识别问题是接下来需要进一步研究的有意义而具有挑战性的课题之一。另外,随着数据采集技术的发展,目前在社会经济、生物医学、环境工程等各个领域出现了大量的超高维数据。因此,在超高维数据框架下,工具变量模型中有效工具变量的识别问题也是一个具有挑战性的课题之一。在接下来的研究中,我们将对这些问题进行深入的探讨和研究。
