基于PID算法的浮桥适时动力固定技术实现
2021-08-30周继波程建生段金辉
周继波,程建生,段金辉
(陆军工程大学 野战工程学院,江苏 南京210007)
浮桥是以浮体作中间桥脚的桥梁,在军事上和民用上都具有广泛的用途。架设在水中的浮桥由于受水阻力和风阻力影响,都需要进行固定,最常见的固定方法是投锚固定。当河底不适宜投锚时往往需要采用其它方法进行固定,动力固定就是一个重要的方法。浮桥动力固定[1-2]是利用桥脚舟自带的动力或专用汽艇的动力来克服浮桥在水中承受的风阻力和水阻力及通载时产生的附加阻力等。其主要特点是快速,不需投起锚,且不受水深、河床土质等条件限制。本文主要针对某带式浮桥在一般河流环境下,采用桥轴线位移监测的方法,建立浮桥数学模型,通过PID控制算法,计算研究在水流作用下动力固定时浮桥的运动和汽艇的推力输出情况,并进行了现场试验,为浮桥动力固定技术在实际中的应用提供参考。
1 浮桥数学模型建立
为了建立浮桥的运动学和动力学方程,考虑浮桥的一段,在河流中具有横荡、纵荡和艏摇三个自由度,地球自转不影响地心加速度的质量。
1.1 坐标系
在研究浮桥运动时,将用到以下坐标系:固定在地球上的惯性坐标系和固定在舟体上的附体坐标系,如图1。
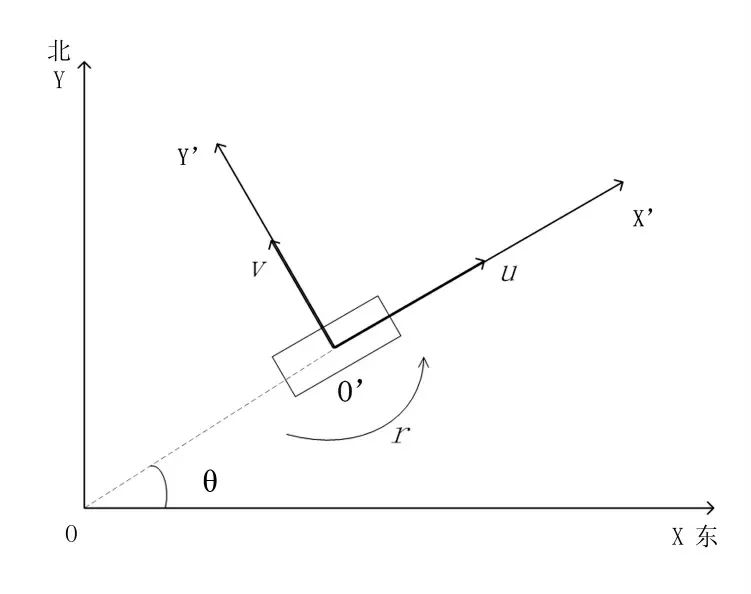
图1 浮桥固定坐标系与附体坐标系
惯性坐标系:又称地球坐标系、固定坐标系。惯性坐标系有多种形式,最常用的一种是北东坐标系。北东坐标系(O-XY)位于静水平面内,O是惯性坐标系原点,是固定于地球表面的任意一点,OX指向正东,OY指向正北,构成了一直角坐标系。
附体坐标系:又称为随桥坐标系,(O′-X′Y′)固定在浮桥上,随浮桥运动,它的坐标原点可以取在重心上,也可以取在水平面,O′X′轴垂直于浮桥横剖面,并指向浮桥架设方向;O′Y′轴垂直于浮桥纵剖面,沿水流方向。惯性坐标系到附体坐标系旋转角为θ。
1.2 浮桥控制模型
当只考虑横向速度时

其中,ν为横向速度。
浮桥架通后,进行动力固定时,只需考虑浮桥横向单自由度,设随体坐标系原点和重心重合,浮桥动力固定涉及横荡的低频运动线性方程为:

其中m为浮桥的质量,y为随体坐标下浮桥横向位移值,y=Ycosθ-Xsinθ,yv˙为浮桥在横荡上的附加质量,yv为浮桥在横向的附加阻尼。水阻力可由经验公式fv=Cρv2ΩH/2求得,C为总阻力系数,ρ为水的密度,v为计算流速,ΩH为桥脚舟浸水部分垂直于水流方向的最大横剖面面积(ΩH=Bh吃水),B为桥脚舟的型宽,h吃水为桥脚舟吃水深度。
2 PID控制器设计
2.1 PID控制原理
经典的PID控制因其算法简单、可靠性强、物理意义明确而被大量地应用于各种控制系统中,PID控制系统原理图如图2所示。PID控制器根据给定值r(t)与实际输出值c(t)得到控制偏差e(t)=r(t)-c(t),将偏差进行比例(P)、积分(I)、微分(D)运算,再对运算结果进行组合构成控制量,对被控对象进行控制。PID的控制规律为:

图2 PID控制系统原理图

将其写成传递函数形式为:

其中,kp代表比例系数,Ti代表积分时间常数,Td代表微分时间常数。
2.2 PID控制策略
本文主要研究浮桥横向位置的保持,即设计的控制器主要用于使被控浮桥桥轴线保持在给定位置的一定范围内。控制策略采用单环控制和双环控制,如图3、图4,双环控制内环控制汽艇发动机转速,外环控制浮桥横向位置。

图3 浮桥动力固定单环控制结构框图

图4 浮桥动力固定双环控制结构框图
直流电机的传递函数通常可用一个一阶环节进行近似。

考虑静水中的情况,浮桥横荡低频运动线性数学模型可表示为:

整理得到浮桥传递函数的形式为:

实际中,由于浮桥横向速度较小,可忽略附加质量和附加阻尼。模型简化为:

故简化的浮桥传递函数的形式为:

2.3 PID控制器仿真分析
本文首先搭建PID控制模型,再对该控制模型的性能进行仿真分析。
选取一段浮桥(3节)作为被控对象,本节的主要目标是设计控制器对浮桥横向位移进行控制,因此在设计的过程中,选取期望的横向位移为0m,即施加控制后浮桥横向位移可以得到完全控制。
本节在Simulink中使用工具自带的PID Controller模块搭建PID控制模型,假定初始位移为0m,期望位移为0m,初始流速为0m/s,在20s时阶跃为2.5m/s,仿真采样时间间隔为1s。PID整定采用经验法,仿真结果如图5-图6所示。
从图5、图6可知,流速发生阶跃变化后,由于控制系统控制力作用,浮桥横向位移偏移不会超过0.3m,且最终会逐渐趋近于0,PID控制器完全满足浮桥动力固定控制系统的性能要求。双环控制比单环控制多了发动机转速控制内环,用于控制转速的稳定性,保证较小超调量和较好的稳定性,抗扰性要优于单环控制。

图5 单环控制浮桥横向位移、速度变化

图6 双环控制浮桥横向位移、速度变化
2.4 试验验证
现场采用数节舟进行试验,岸边舟采用系留钢索系留,陆侧第一个河中舟采用斜张纲固定,其余舟不固定。在浮桥段水侧下游固定安装有自适应推力系统的汽艇,并在岸上、汽艇和相应桥脚舟上安装北斗位置监测终端。用上游汽艇顶推浮桥,模拟流速变化,在试验初始阶段,浮桥会产生向下游的偏转,北斗监测机实时测量桥轴线位移变化,传输至控制系统,经控制器算术运算,向下游汽艇发出指令,下游汽艇自适应适时增加推力,浮桥段又回复到初始的桥轴线,下游汽艇的动力能与上游汽艇模拟产生的水阻力保持适时平衡。
试验后解算“偏(浮桥)-推(汽艇)-稳(轴线)”(记为PTW)典型循环过程中浮桥及汽艇在水流方向上的位移偏移量,绘制于图7中。由图7可见,初始上游汽艇顶推浮桥段产生位移后,动力调节系统能快速接收控制指令产生顶推力,将浮桥轴线稳固在浮桥基线0.3m范围内。
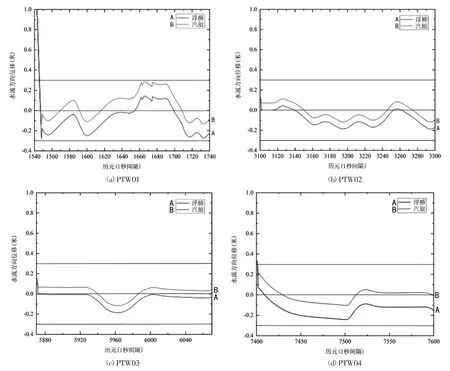
图7 各历元段下浮桥及汽艇在水流方向上的解算位移偏移量
3 结论
本文建立了浮桥数学模型,采用监测桥轴线位移的方法,着眼于自动控制技术的实现,设计了动力固定浮桥的PID控制系统,通过仿真和试验表明,通过PID控制可以实现浮桥的适时动力固定,保持浮桥的横向稳定,且具有较快的响应速度。
