6Sigma正交试验在侧围外板冲压CAE尺寸精度优化中的应用
2021-08-30徐大君曾兵华李伟明
徐大君,曾兵华,李伟明,陈 俊
(重庆长安汽车股份有限公司,重庆 401120)
0 引 言
侧围外板是汽车覆盖件中外形尺寸最大、形状最复杂、装配关系最多的冲压零件。尺寸精度是衡量外覆盖件重要指标之一,不同材料与不同成形工艺对其影响较大。以某车型侧围零件为例,结合有限元仿真模拟和数理统计的方法进行分析,解决侧围外板尺寸精度不足的问题。
正交试验是研究多因素多水平的一种试验设计方法,根据正交性从全面试验中挑选部分有代表性的点进行试验,这些有代表性的点具有均匀分散、齐整可比的特点。当试验涉及的因素在2个或2个以上,且因素间可能有交互作用时,试验工作量会很大,甚至难以实施。针对该困扰,正交试验是更好的选择。正交试验设计的主要工具是正交表,试验者可根据试验的因素数、因素的水平数以及是否具有交互作用等需求查找相应的正交表,再依托正交表的正交性从全面试验中挑选部分有代表性的点进行试验,可以实现以最少的试验次数达到与大量全面试验等效的结果,在较短的时间内得到理想的试验结果和科学结论。
基于AutoForm有限元软件分析侧围外板上梁尺寸超差情况,通过修改正压料力、侧压料力和过翻边量,得出多组CAE分析结果,利用数理统计软件Mintab对影响零件尺寸的因素进行分析,找出对尺寸影响较大的因子,建立数学模型并进行优化分析。具体的实施过程:先通过修改不同数值的正压料力、侧压料力和过翻量得出多组CAE分析结果,然后对因子进行正交试验,根据试验结果建立正压料力、侧压料力和过翻量的回归方程,最后通过对回归方程的求解得到最优解。
1 整改前侧围外板状态
某侧围外板前侧与前门上侧匹配尺寸超差频次达90%,且左右侧围超差频次相当,影响整车外观和生产效率。为解决该处间隙不均的问题,装车前操作人员需要调整零件或对左右侧围模具进行返修,影响生产效率且浪费成本。侧围前侧间隙超差的位置如图1所示,140、141、136三点为检测点。
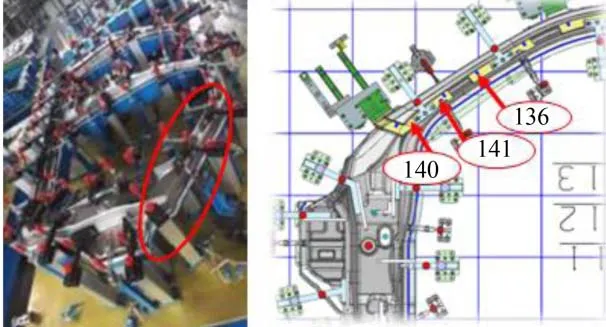
图1 侧围外板前侧间隙超差位置
对上述3个点的过程能力进行分析,判定指标为PP≥1.33,PPK≥1.33(PP表示潜在的过程性能,显示了总过程分布宽度与工程规范之间的关系,总过程变差变小时,PP就会变大;PPK显示了实际的过程性能,同时考虑了过程对中性及过程总变差),计算公式如下:
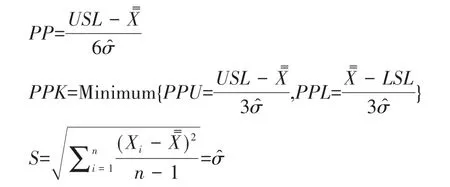
其中,USL、LSL为样本上、下限,为样本均值。
对上述3个检测点(140、141、136)现场检测数据进行分析后结果如图2~图4所示。140号点PP=1.80、PPK=-0.17,过程能力不足;141号点PP=1.87、PPK=-0.15,过程能力不足 ;136号点PP=1.59、PPK=1.58,过程能力满足。
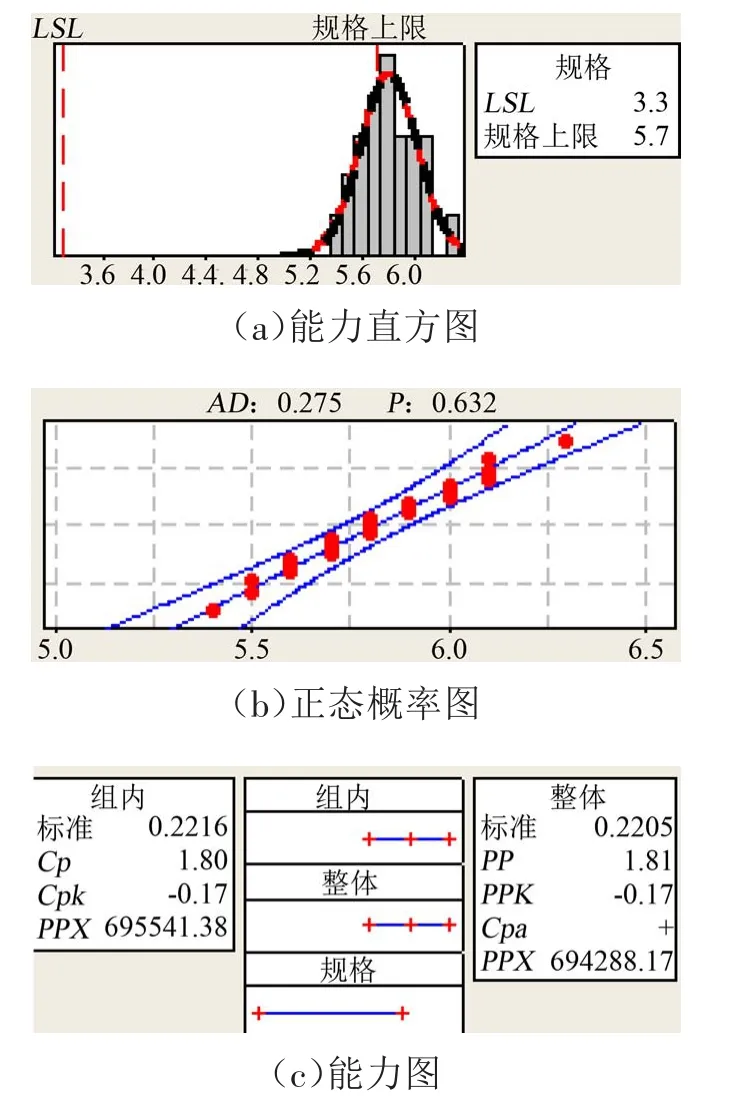
图2 140号点检测数据分析
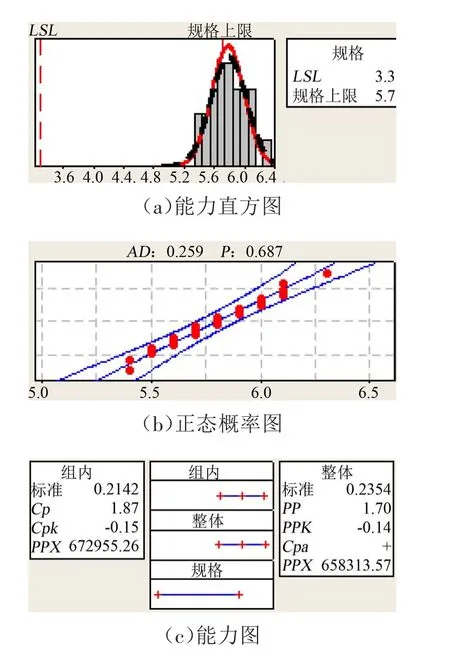
图3 141号点检测数据分析
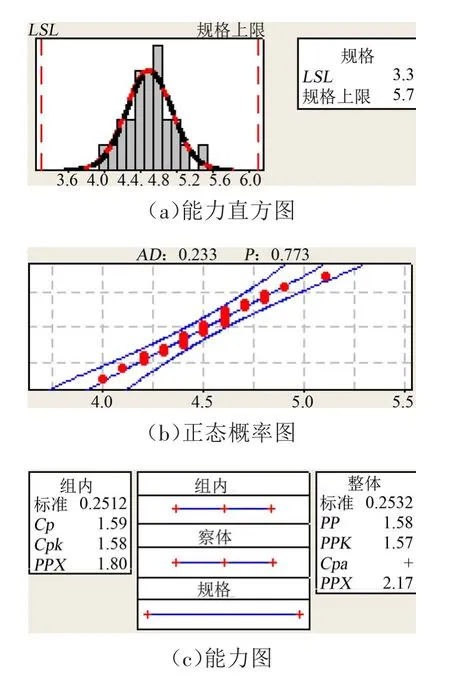
图4 136号点检测数据分析
对3个点的过程能力进行分析可知,140、141两点的PPK为负值,说明数据偏离受控制一侧,距1.33目标较大,所以需要整改提升这2个检测点的过程能力。
2 正交试验设计
正交试验是MPI仿真分析设计的科学试验方案,用最少的试验次数获取响应(试验结构)和因素(工艺参数)之间关系的最多信息。仿真分析后,需要对获取的试验结果进行极差分析与方差分析,确定影响侧围尺寸精度试验指标的主、次要因素及各因素对试验指标影响的显著程度,得出试验因素的最优水平和组合,即最佳工艺参数组合方案。
2.1 因素选取
经综合排查分析,模具成形时材料流动偏向一侧导致零件轮廓攒动,该位置的间隙超差由整形模侧压料整形导致,整形模成形部位如图5所示,影响此处间隙的因素有侧压料力与过翻边量:①侧压料力偏小,侧整刀块整形时压不住材料,材料流动导致零件边界移动;②零件成形后材料完全硬化,处于塑性阶段的材料恢复导致零件边界收缩;③侧压料力和过翻边量的相互作用。
图5 整形模成形部位
2.2 因子高低水平确定
因模具已经制造完成,更换氮气缸成本太高,现采用减小有效压料面积、增大压强的思路进行整改,现场侧压料力为38 kN,通过减小压料面积可以达到54 kN的压力效果,实际过翻边量为0.2 mm,此处按照经验最大可以做到1 mm,因子水平如表1所示。
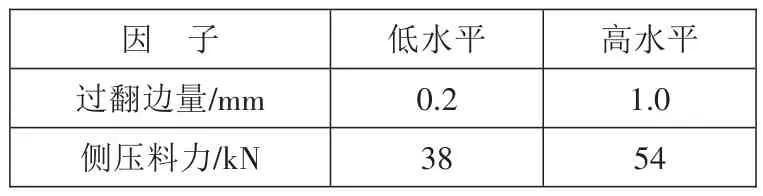
表1 因子水平
2.3 响应产品偏移量指标
查看零件GTD技术文件,此处公差为±0.5 mm,按照该数据在Mintab的响应优化器中对零件偏移量进行设置,如图6所示。
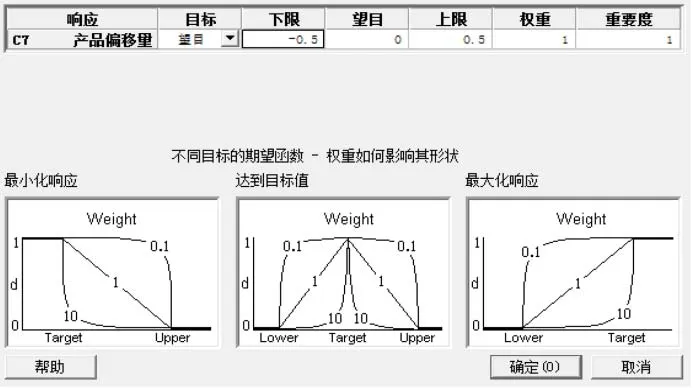
图6 零件公差设置
2.4 Mintab中设置因子
得到试验所需的数据:①创建因子,并定义因子高低水平;②全因子设计,中心点数为2,仿行数为1,区组数为1。
针对正交表(见图2)对应因子进行CAE仿真分析,得到响应值(零件偏移量)。侧压料力直接在AutForm中进行设置,过翻边量在CATIA中进行参数化设计。
2.5 分析因子设计
ANOVA表如表3所示,拟合总效果判定系数R2(R-Sq)及修正的判定系数数值越接近1越好。
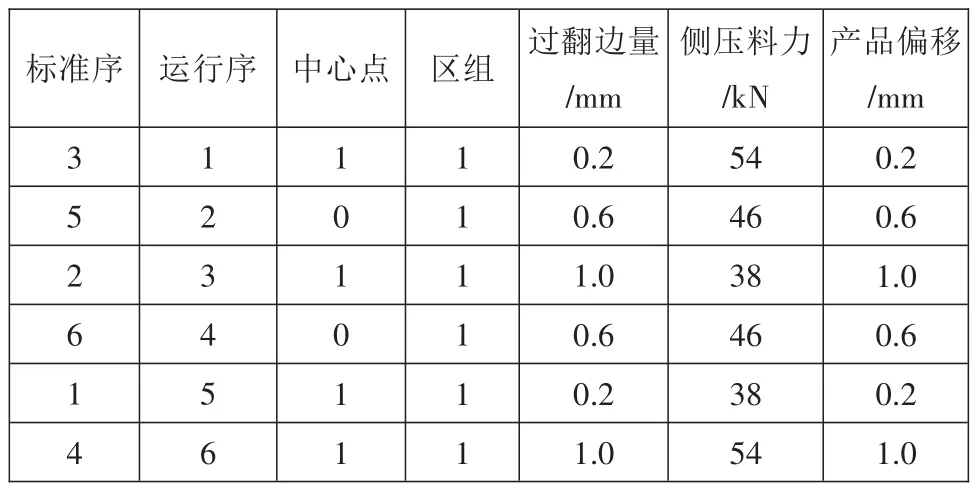
表2 正交表
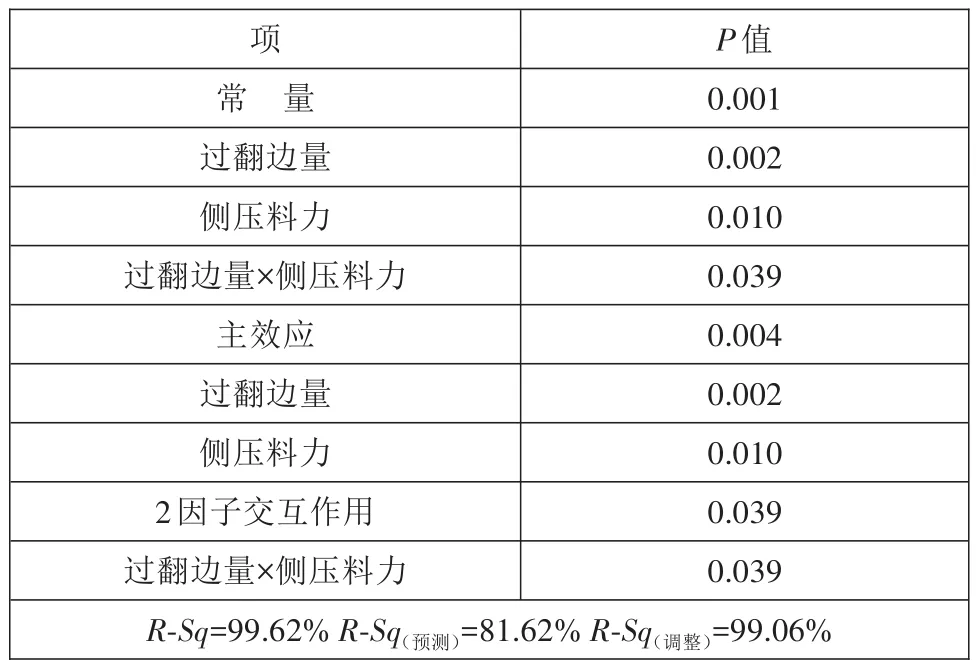
表3 ANOVA表
由回归分析中的平方和分解公式可知:
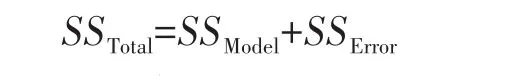
其中,SSTotal为总变差;SSModel为过程变差;SSError为测量系统变差。
考虑SSTotal和SSModel中的比率,定义平方(R-Sq):
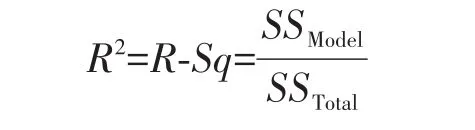
残差图分析需要满足以下准则:①响应变量拟合值保持方差奇性(如果是直线型,可能缺乏一次项;如果存在明显的曲率,可能需要增加平方项);②正态性检验图服从正态分布且散点随机分布不存在弯曲趋势,如图7所示。
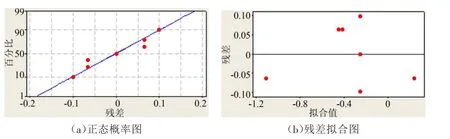
图7 偏移量残差
假设检验模型可以确定事情的结果是偶然发生还是实质性变化。在假设检验模型中,P值表示对原假设的支持程度。对应回归项的P值<0.05时,则表明应该拒绝原假设,即模型有效;对应回归项的P值>0.05时,则无法拒绝原假设,即判定模型无效。从表3可以看出,过翻边量、侧压料力及两者交互作用的P值<0.05,拒绝原假设,表示其三者为影响响应因子的主要因素。
响应曲面如图8所示,过翻边量、侧压料力及其交互效应对响应偏移量影响显著。

图8 响应曲面
根据拟合系数和残差图分析正交表数据,拟合的数学模型均满足要求,借助假设检验判定过翻边量、侧压料力以及二者交互作用是影响侧围前侧间隙精度的主要因子。通过响应优化器得出最优参数为:过翻边量0.952 8 mm,侧压料力21 kN,如图9所示。
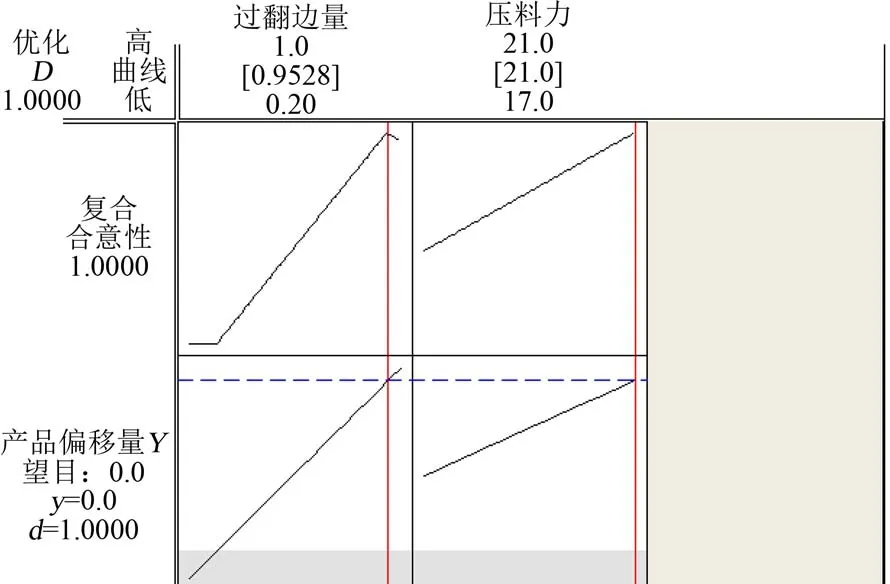
图9 响应的优化值
3 最优解CAE验证
依据上述优化结果,在AutoForm软件中过翻边量取1.0 mm,侧压料力设置为21 kN,模拟验证得出零件偏移量为-0.05 mm,而零件间隙公差为±0.5 mm,CAE分析数值可接受,如图10所示。
4 现场验证
AutoForm软件模拟时侧压料器为全型面压料,先计算50 kN全型面侧压料时的压强。为了使现场和理论分析的压强相等,在现场侧压料力不变的情况下减小侧压料的有效压料面积。
过翻边量直接在加工数据上修改为1.0 mm。按照分析优化后,对侧围前侧3个点随机各抽取25组间隙值进行过程能力的判定,如图11~图13所示。140点的P值>0.05,数据服从正态分布,PP=1.40、PPK=1.38,过程能力稳定;141点的P值>0.05,数据服从正态分布,PP=1.80、PPK=1.65,过程能力稳定;136点的P值>0.05,数据服从正态分布,PP=1.46、PPK=1.41,过程能力稳定。
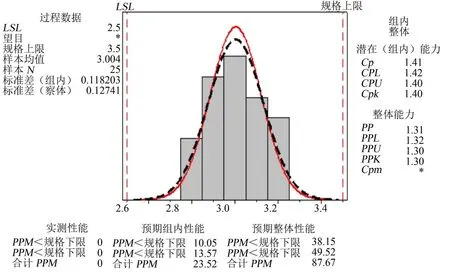
图12 141点过程能力图
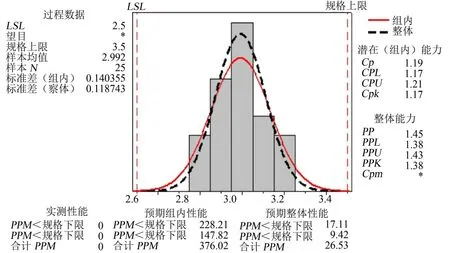
图13 136点过程能力图
上述136、140、141三点的测量数据服从正态分布,PP≥1.33、PPK≥1.33,过程能力受控稳定,整车侧围上侧的间隙故障率由90%降至为3%,如图14所示。
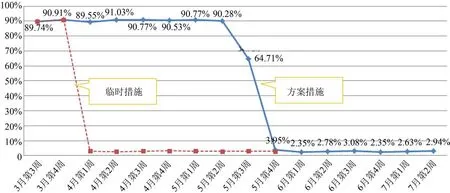
图14 侧围前侧故障率
5 结束语
利用数理统计软件Mintab和成形模拟软件AutoForm的优势,为工艺设计和现场整改提供有力参考。该方法可以解决设计阶段工艺参数多且交互作用试验次数多的问题,为提高零件开发的成功率和成形质量提供了保障。最终形成一套提升冲压CAE尺寸精度的解决方案,缩短了模具开发周期,降低了模具的整改和调试工时,为类似零件模具开发奠定基础。
