从属于指数函数的星像函数子类的四阶 Hankel 行列式

张海燕, 汤 获, 马丽娜

(赤峰学院数学与计算机科学学院, 赤峰 024000)

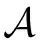
(1)

的函数族.

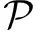
1992年,MA和MINDA[1]引入某类星像函数类S*(φ):

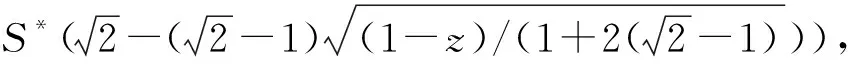
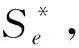
另一方面,对于不同解析函数类的Hankel行列式研究一直是热点问题之一. 1966年,POMMERENKE[5]定义了解析函数f的q阶Hankel行列式Hq(n). 很明显,当q=2,n=1时,|H2(1)|即是Fekete-Szegö泛函[6-11]. 近年来,许多学者对各类解析函数的二、三阶 Hankel 行列式做了大量研究[12-24]. 如:研究了与指数函数有关的星像函数类的二、三阶 Hangkel 行列式[12-14];研究了有界转动、星像和凸像函数类的三阶Hankel 行列式[15];研究了近于凸函数类的三阶Hankel 行列式[17].

但是,目前对于与指数函数有关的函数类的 Hankel 行列式的研究都仅基于二阶和三阶的情形,而对四阶 Hankel 行列式的研究还不多见. 基于以上启发,本文主要研究了与指数函数有关的星像函数类的四阶 Hankel 行列式H4(1), 得到其上界估计.

1 预备知识

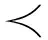
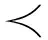
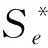
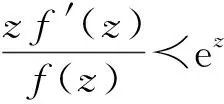
(2)

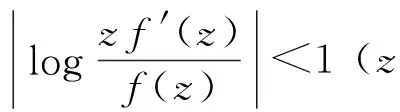
其中,a1=1,n≥1,q≥1.特别地,有

下面给出本文所需用的引理.

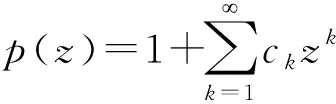
及

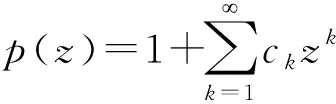
及|cn|≤2(n=1,2,…).

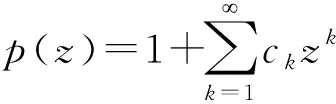
|cn+k-μcnck|<2,

2 主要结果

下面给出本文的主要定理.

(3)

3a2a4)z6+….

(4)

令

(5)

由式(5)知,

(6)

分别比较式(4)、(6)两边关于z、z2、z3、z4、z5、z6的系数,可得

(7)

由引理2,易证 |a2|=|c1/2|≤1.而由引理1,可得

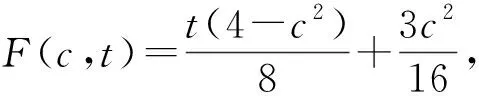
故F(c,t)在[0,1]关于t是单调递增函数. 因此,F(c,t)在t=1取得最大值,即

易证G(c)在c=2处取得最大值,即|a3|≤G(2)=3/4.

又

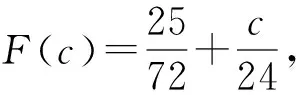
类似地,因为

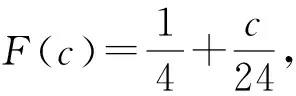
又

令

则

因此,c=0 是方程F′(c)=0 的根. 又因为F″(0)<0,所以,F(c)在c=0处取得最大值,即|a6|≤F(0)=17/60.

又

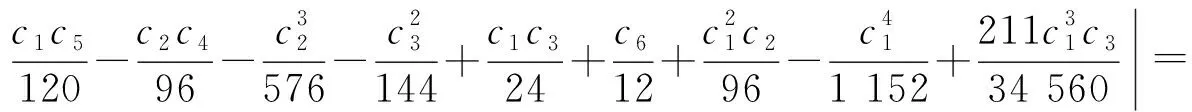
令

进而可得F′(c)≥0.因此,F(c)在c=2处取得最大值,即|a7|≤F(2)=59/80.证毕.

(8)

证明通过式(7)可得

由引理1可知

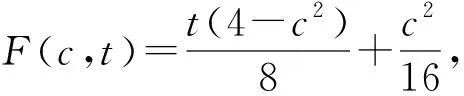
因此,F(c,t)在[0,1]关于t是单调递增函数. 故F(c,t)在t=1处取得最大值,即

同理易证G(c)在c=0处取得最大值,即

证毕.

(9)

证明由式(7)可得

由引理2和引理3可得

证毕.

(10)

证明由式(7)可得

由引理1可得

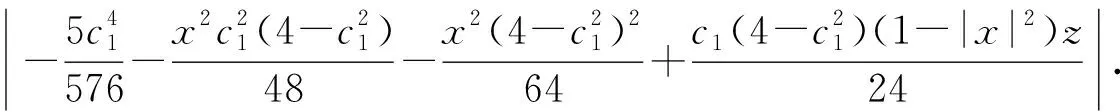
令

因此,F(c,t)在[0,1]上关于t是单调递增函数,从而可得F(c,t)在t=1处取得最大值,即

设

则

(11)

令

因此,F(c)关于c单调递增,故F(c)在c=2处取得最大值,即

证毕.

(12)

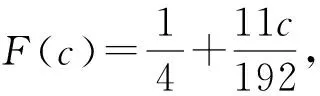
证毕.

(13)

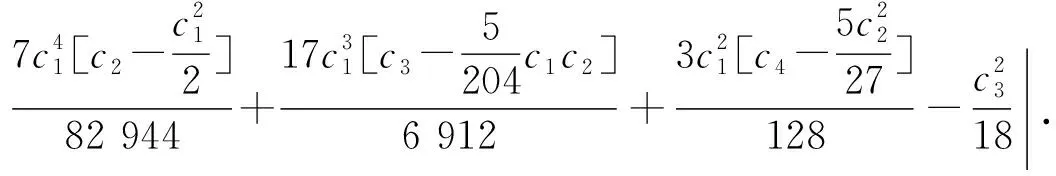
令

因此,F(c)关于c单调递增,故F(c)在c=2处取得最大值,即

证毕.

(14)

证明因为

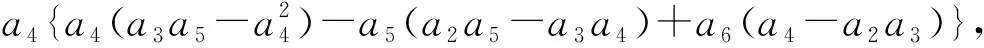
所以,由三角不等式可得

|a4||a5||a2a5-a3a4|+|a4||a6||a4-a2a3|.

(15)

将式(3)、(8)～(13)代入到式(15),即得式(14). 证毕.