基于复杂网络的混合数据聚类分析

王依赟，许 英

(新疆财经大学 统计与数据科学学院，乌鲁木齐 830012)

随着社会的高速发展，人们对数据价值的认识逐渐加深。在这个大数据时代，人们希望从纷繁复杂的数据中提取到有价值的信息。聚类分析是数据挖掘的一个重要算法，是以相似性为基础，在一个聚类中的对象之间比不在同一聚类中的对象之间具有更多的相似性。

近年来，聚类算法中针对混合数据聚类最著名的方法是Huang提出的K-prototypes算法[1]，该方法结合K-means与K-modes算法对混合属性数据进行划分，通过参数μi来控制数值属性与分类属性在聚类过程中的权重。

本文把复杂网络相关知识应用到混合数据中，针对混合数据的基于熵的相似矩阵，利用阈值法生成0-1矩阵(即复杂网络的邻接矩阵)，进而构造复杂网络，对生成的复杂网络进行社团结构划分，复杂网络的一种社团结构划分就对应混合数据的一种聚类结果。

本文用三个数据集作为实验对象，通过和混合数据的聚类算法：DP-MD-FN、K-Prototypes、KL-FCM-GM、iEKP、OCIL算法进行比较，实验结果表明利用复杂网络社团结构划分算法得到的混合数据的聚类结果的准确性更高。

1 混合数据相似矩阵

1.1 概念

1.2 数值型的相似性度量

数值型的相似性度量可以采用欧氏距离，两个数值型数据的欧氏距离定义为：

dist(xi,xj)=‖xi-xj‖2

(1)

为了计算混合数据的相似度，采用一个单调递减函数将距离dist转化为相似度Sr[2-3],它是由一个指数函数给出：

(2)

其中Sr的值越接近1，两个对象越相似。

1.3 分类型的相似性度量

(3)

(4)

(5)

(6)

(7)

将式(7)代入式(4)，可以得到分类属性的最终相似性测度，如下所示：

(8)

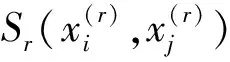
1.4 混合型的相似性度量

数值部分的相似性是作为一个整体来对待的，而分类部分的相似性是作为个体来计算。因此，两个混合类型对象xi和xj之间的相似性(表示为S(xi,xj))定义为：

(9)

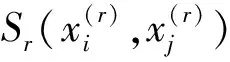
2 转换混合数据集为复杂网络

各类数据转换为复杂网络数据将会有更多的附加信息，其中最重要的是结构或拓扑信息，网络拓扑能够以简洁的方式对数据交互进行系统化的编码，从本地结构信息到全局结构信息。构建网络的方法有很多种，如阈值法、最小生成树法等等,本文将采用阈值法将混合数据转换为复杂网络数据。

2.1 相关网络法

设定阈值参数s，以每个混合数据对象为节点，若任意两个混合数据的相似性大于或者等于所给定的阈值s(s∈[-1,1]),则这两个混合数据之间有边相连，小于阈值的不相连。具体定义如下：

(10)

可以得到混合数据间的相似度的邻接矩阵A=(Aij)n×n,基于该邻接矩阵，构建相对应的复杂网络。

2.2 三种混合数据集对应的相关网络

为了验证本文方法的有效性，选用UCI Machine Learning Repository里的Credit Approval数据集、Heart Disease数据集以及Australian Credit Approval这三个实际混合数据集，数据集的真实类别属性剔除，并作为原始数据分类的基准对各类算法的准确性进行评估。数据集的具体信息如表1所示。

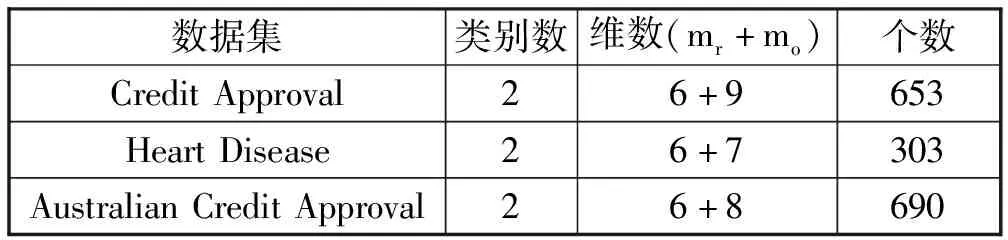
表1 三个实际混合数据集

三组数据集在不同阈值下对应了不同的复杂网络。Heart Disease混合数据集在阈值s为0.1～0.8时，连通分支数均为1，当阈值s为0.9时，连通分支数为5,不同阈值对应的网络边数和连通分支数如表2所示。

表2 混合数据集Heart在不同阈值下对应的复杂网络

Credit Approval混合数据集在阈值为0.1～0.3时，连通分支数为1，当阈值为0.35～0.8时，连通分支数为2，阈值为0.8时，连通分支数为4，阈值为0.9时，连通分支数为5，不同阈值对应的网络边数和连通分支数如表3所示。

表3 混合数据集Credit在不同阈值下对应的复杂网络

Australian Credit Approval混合数据集在阈值为0.1～0.3时，连通分支数为1，当阈值为0.35～0.7时，连通分支数为2，阈值为0.8～0.9时，连通分支数为4，不同阈值对应的网络边数和连通分支数如表4所示。

表4 混合数据集Australian在不同阈值下对应的复杂网络

3 聚类结果分析

3.1 复杂网络社团结构划分结果

本节基于上述三个实际混合数据集所构造的复杂网络，利用复杂网络社团结构划分的四种算法Fast greedy(FG),Leading eigen(LE),Louvalin(LOU),Walktrap(WA)算法对复杂网络进行社团结构划分，记录不同阈值下的复杂网络社团结构划分的NMI值和分类数。

混合数据集Heart在0.1～0.9阈值下对应复杂网络的社团结构划分的NMI值和分类数k如表5所示，由表5可知，混合数据集Heart在阈值为0.1时，LE算法得到的NMI值最大，NMI=0.413，该社团结构划分算法的结果即为所对应的Heart混合数据集的聚类结果。

表5 混合数据集Heart在不同阈值下对应复杂网络的社团结构划分NMI值和分类数k

混合数据集Credit在0.1～0.8阈值下对应复杂网络的社团结构划分NMI值和分类数k如表6所示，由表6可知，混合数据集Credit在阈值为0.35时，LOU算法得到的NMI值最大，最大值为0.457，该社团结构划分算法的结果即为所对应的Credit混合数据集的聚类结果。

表6 混合数据集Credit在不同阈值下对应复杂网络的社团结构划分NMI值和分类数k

混合数据集Australian在0.1～0.8阈值下对应复杂网络的社团结构划分NMI值和分类数k如表7所示，由表7可知，混合数据集Australian在阈值为0.35时，FG算法得到的NMI值最大，最大值为0.434，该社团结构划分算法的结果即为所对应的Australian混合数据集的聚类结果。

表7 混合数据集Australian在不同阈值下对应复杂网络的社团结构划分NMI值和分类数k

3.2 混合数据集聚类结果分析

复杂网络的社团结构划分结果对应混合数据集的聚类结果，针对上述结果，表8列出了3.1节的结果和DPC-MD、DP-MD-FN、K-Prototypes、KL-FCM-GM、EKP、OCIL算法在三个混合数据集上NMI值。由表8可以看到，本文所得的三个数据集聚类结果的NMI最大值分别为0.413,0.458,0.434，与其他算法相比效果更好。

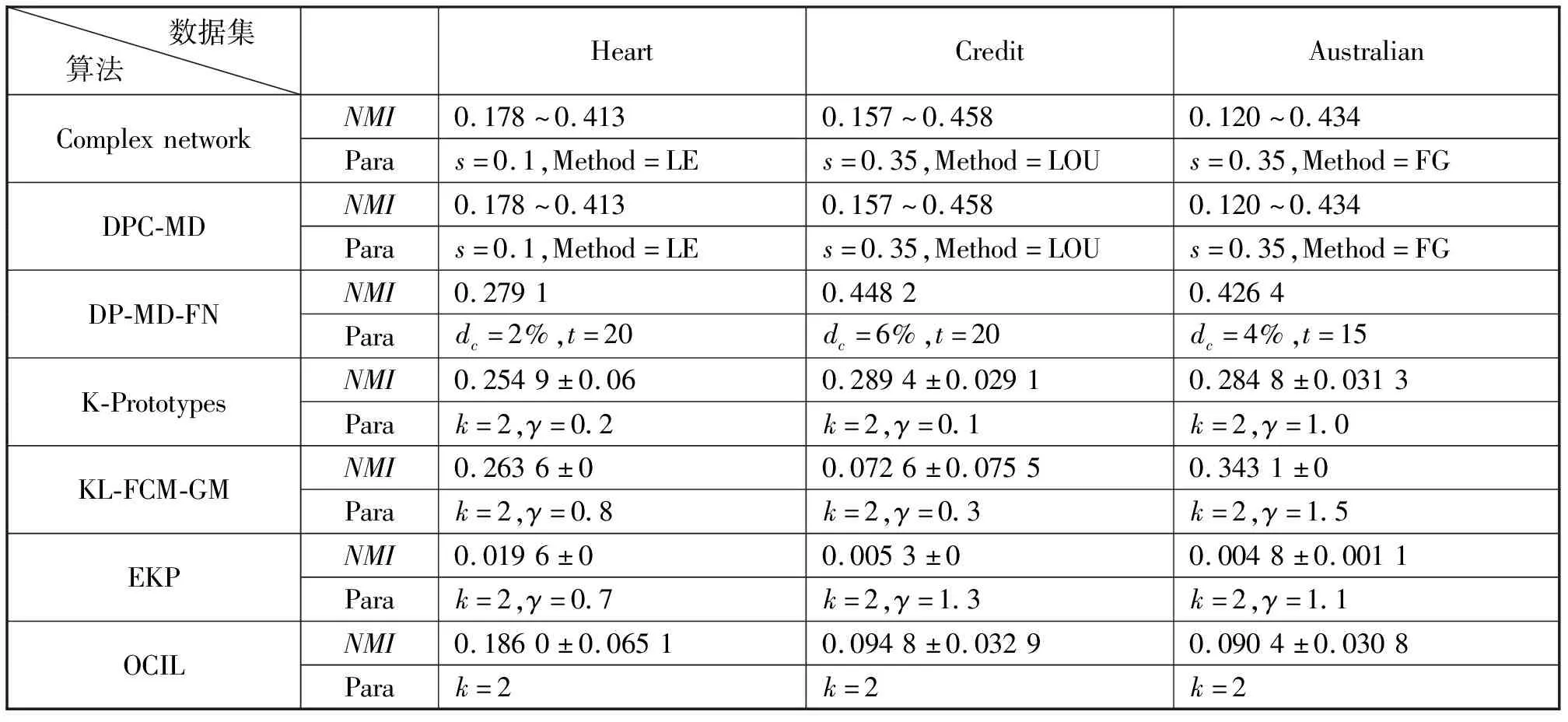
表8 三个混合数据集在多种算法下的NMI值比较

表9列出了3.1节的结果和DPC-MD、DP-MD-FN、K-Prototypes、KL-FCM-GM、EKP、OCIL算法在三个混合数据集上的准确度ACC值。由表9可以看到，本文所得的三个混合数据集的ACC值分别为0.858 1,0.872 9,0.858 0，与其他算法相比效果更好。

表9 混合数据集在多种算法下的ACC值

表10列出了3.1节的结果和DPC-MD、DP-MD-FN、K-Prototypes、KL-FCM-GM、EKP、OCIL算法在三个混合数据集上的兰德指数ARI值。由表10可以看到，本文所得的三个混合数据集的ARI值分别为0.512 9,0.558 9,0.512 6，与其他算法相比效果更好。

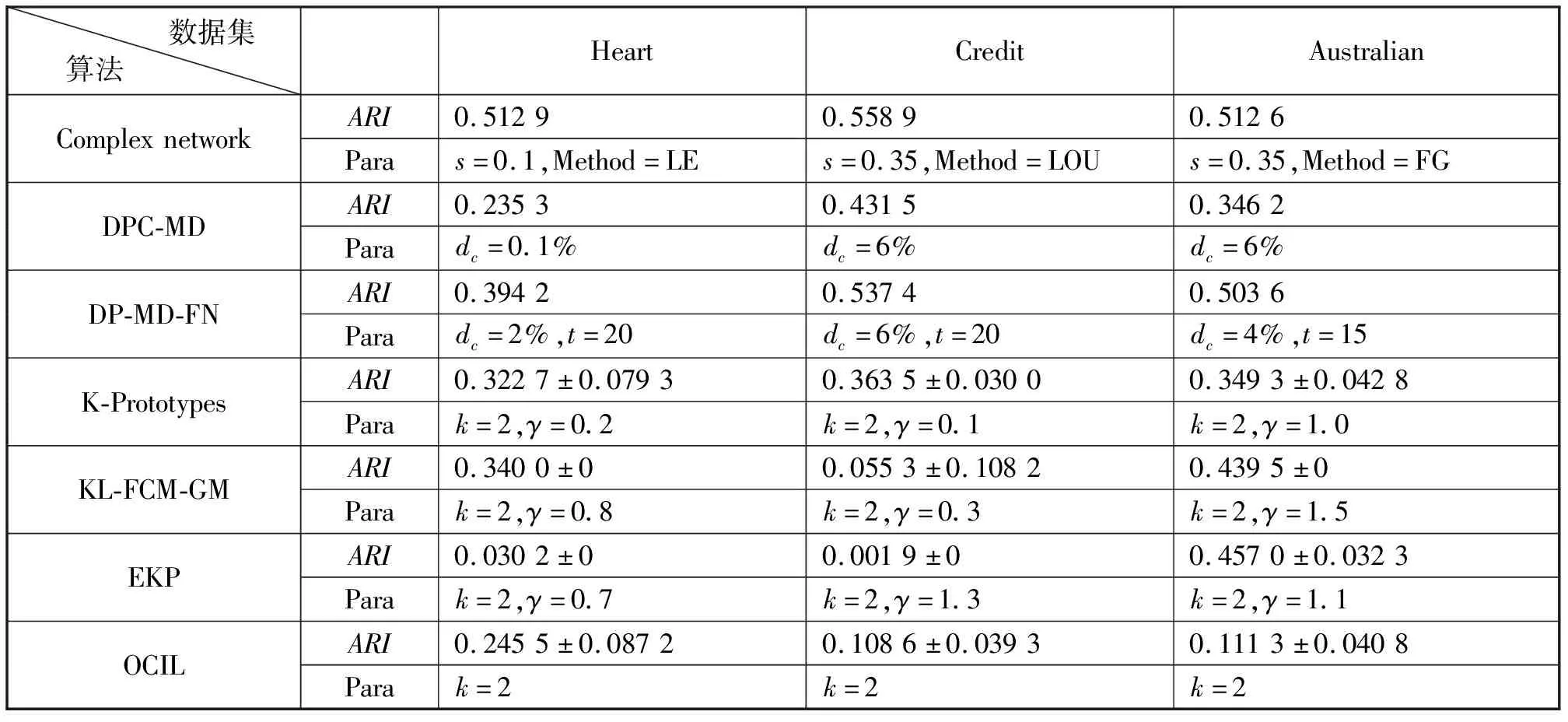
表10 混合数据集在多种算法下的ARI值

4 结论

数据挖掘擅长处理各类数据并从中发现隐藏规律，复杂网络着重于从网络角度描述系统结构功能并发掘其普适规律，将复杂网络相关知识应用于混合数据中，将有效解决混合数据在聚类分析与处理方面的瓶颈。

针对混合数据集的聚类问题，本文把复杂网络相关知识应用到混合数据中，针对混合数据的基于熵的相似矩阵，利用阈值法生成复杂网络的邻接矩阵，对生成的复杂网络进行社团结构划分，复杂网络的一种社团结构划分就对应混合数据的一种聚类结果。该方法进一步 探索了数据挖掘和复杂网络之间的关系，也为混合数据的处理提供了新的方向。

通过与现有的聚类方法进行比较，本文的NMI、ACC和ARI值均有所提高，结果表明本文提出的方法将有助于提高混合数据聚类分析的准确度，从而为今后复杂网络和数据挖掘知识的融合提供强有力的依据。