点缺陷对4H-SiC的影响

苏晋阳，郭瑞贤，刘淑平

(太原科技大学 应用科学学院，太原 030024)

碳化硅(SiC)是一种新型宽带隙半导体材料[1]，具有优秀的物理化学性质，并且在高温、高频和高功率器件领域得到了广泛的应用[2]。晶体结构分析表明，SiC具有250多种同型异构体[3]，工业上制造半导体时通常使用3C-SiC,4H-SiC,6H-SiC[4].如图1所示,3C-SiC是C-Si双原子层按照ABC的堆垛顺序排列，4H-SiC是C-Si双原子层按照ABCB的堆垛顺序排列，6H-SiC是C-Si双原子层按照ABCACB的堆垛顺序排列。其中4H-SiC是这三种常用半导体中带隙最宽，电子迁移率最高，符合大功率电子器件的需求[5]。4H-SiC作为一种宽带隙(3.26 eV)半导体，与Si相比，4H-SiC带隙约为Si(1.12 eV)的3倍[6]，电子漂移速度比Si高2倍[7]，热导率为Si的3倍，临界击穿场强度大约为Si的8-10倍[7]。因此，4H-SiC是极端工作条件下的理想电子学材料[8]。本文主要从两个方面进行分析，一，通过第一性原理进行结构优化得出4H-SiC上每一个含缺陷薄膜的态密度(DOS)与完美薄膜的DOS比较得出薄膜能带结构及电子状态的变换。二，计算缺陷形成能重而得出缺陷形成的难易程度。

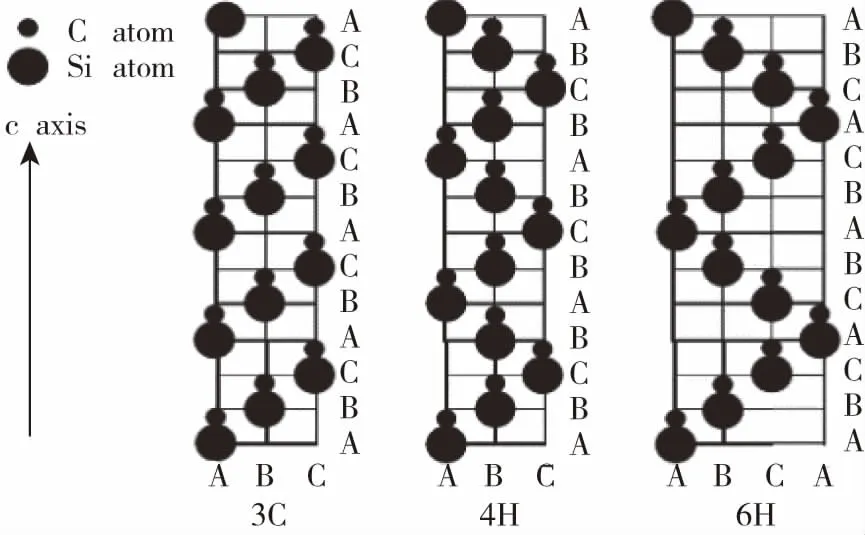
图1 SiC的三种结构

1 计算模型与方法

4H-SiC属于纤锌矿结构，每个晶胞内含有一个Si原子和一个C原子[9]。表示的是计算时4H-SiC完美薄膜表面，4H-SiC薄膜上的碳空位缺陷(VC)和硅空位缺陷(VSi)，硼原子掺杂和磷原子掺杂。所有计算均使用Cambridge Serial Total Energy Package(CASTEP)[10]中执行。通过Broyden-Fletcher-Goldfarb-Shanno(BFGS)[11]方法对晶体缺陷系统进行几何优化，将能量最低结构作为晶体稳态结构。

利用平面波基矢对价电子波函数进行了扩展，其中平面波截止能设定为310 eV，总能量和电荷密度在对Brilouin区的积分计算使用Monkhorst-Pack方案选择k网格点为9×9×4，快速傅里叶变换(FFT)网格取(54×54×45)，自洽收敛精度设定为5.0×10-5eV/atom，每个原子上受到的作用力不大于0.03 eV/Å，原子最大移位的收敛标准为0.001Å，晶体内应力不大于0.05 GPa，交换相关势采用由Kohn-Sham提出的局域态密度近似(LDA)，离子电子之间的相互的作用由Ultra Soft Pseudo Potential(USPP)计算，计算的电子态包括：C:2s2p2，Si:3s23p2，所有计算均在倒易空间中进行。

2 点缺陷形成能计算

在进行晶体生长和离子掺杂过程中，晶体中形成每类缺陷的概率大小，可以用缺陷形成能Ef(Xq)进行描述。缺陷出现的概率与缺陷的形成能[12]大小呈反比。此外，因为缺陷带电，所以计算形成能时需要考虑缺陷原子化学势和电子交换势能。[13]缺陷带电荷量为q时，晶体表面缺陷形成能由等式(1)定义：

Ef(Xq)=Etot(Xq)-Etot(SiC(sur))-

∑ηiμi+qEF

(1)

(2)

(3)

(4)

其中，Etot(Xq)表示4H-SiC晶体中包含缺陷X的总能量；SiC(sur)是同等大小下4H-SiC的本征能量；ηi表示晶体中缺陷或杂质的原子数，i表示缺陷原子类型，ηi>0表示缺陷或杂质原子的增加；ηi<0表示缺陷或杂质原子的减少；μi表示原子化学势能；EF是电子交换势能；q表示缺陷的带电状态的数目，如果是中性的缺陷则q=0，如果减少了一个电子q=+1，添加了一个电子q=-1.在式(2)中，μSi是一个变量，受SiC生长环境或退火过程条件的影响，如晶体生长过程的不同温度和压强等。式(2)表示了C和Si原子化学势的变化范围。Si原子的化学势和C原子的化学势之和等于SiC晶体的化学势时达到稳定的状态。同时式(3)(4)表示了Si原子和C原子的化学势受SiC晶体的化学势的限制。因此，化学势在材料生成焓所确定的范围内变化。

对表1中的形成能的绝对值得大小进行比较可得出在原子空位缺陷和原子掺杂缺陷的过程中，硅原子空位缺陷最容易形成，掺杂原子的性质决定了掺杂所需的形成能的大小。因此可得出在碳化硅材料中，碳原子或硅原子的空位缺陷比原子掺杂缺陷更容易形成，当掺杂缺陷产生时碳原子空位缺陷或硅原子空位缺陷也应当会发生。

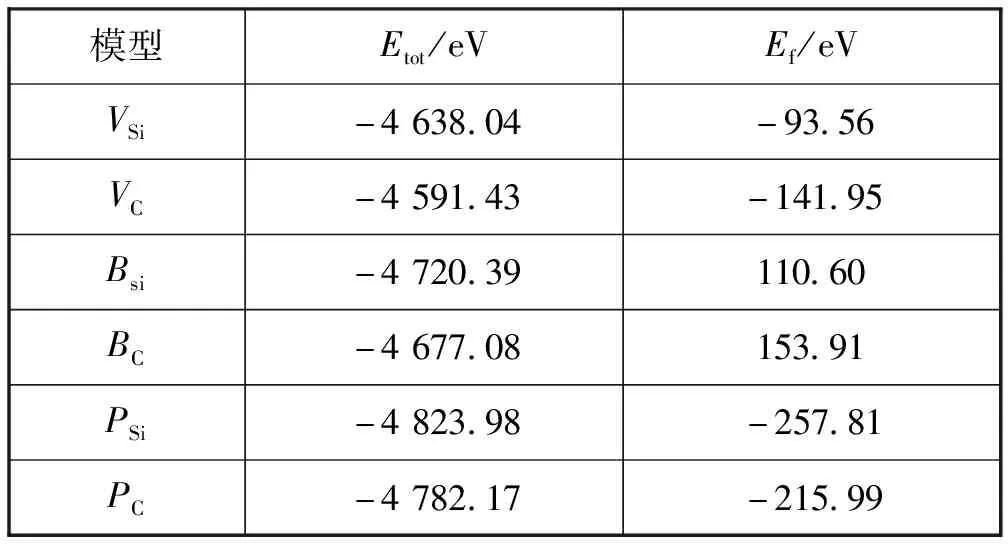
表1 4H-SiC点缺陷形成能

3 原子空位缺陷下的态密度图

3.1 完美4H-SiC的态密度图

本文计算得出4H-SiC本征体的晶格常数为a=b=0.303 9 nm,c=0.994 8 nm与实验值a=b=0.307 3 nm,c=1.005 3 nm相近，数值偏小的原因是通过LDA计算得到的晶格常数要比实验值要小。在相同的条件下计算了4H-SiC薄膜以及4H-SiC薄膜上的点缺陷的能带结构和电子态密度。

从图2(a)的态密度(DOS)可得出SiC材料的能带宽度主要由碳原子与硅原子的P能级决定，由图2(b)可得出在价带区域(负数区域)的态密度主要受C原子的P能级影响，在导带区域的态密度值主要由硅原子的p能级影响。在0.51 eV到2.79 eV范围内态密度等于0,这表示薄膜的禁带宽度为2.28 eV，与实验值Eg=3.26 eV相比仍远小于实验值，这是因为密度泛函理论是一个基态理论，计算出的禁带宽度要小于实验值，计算的误差为30%，在误差允许的范围内。

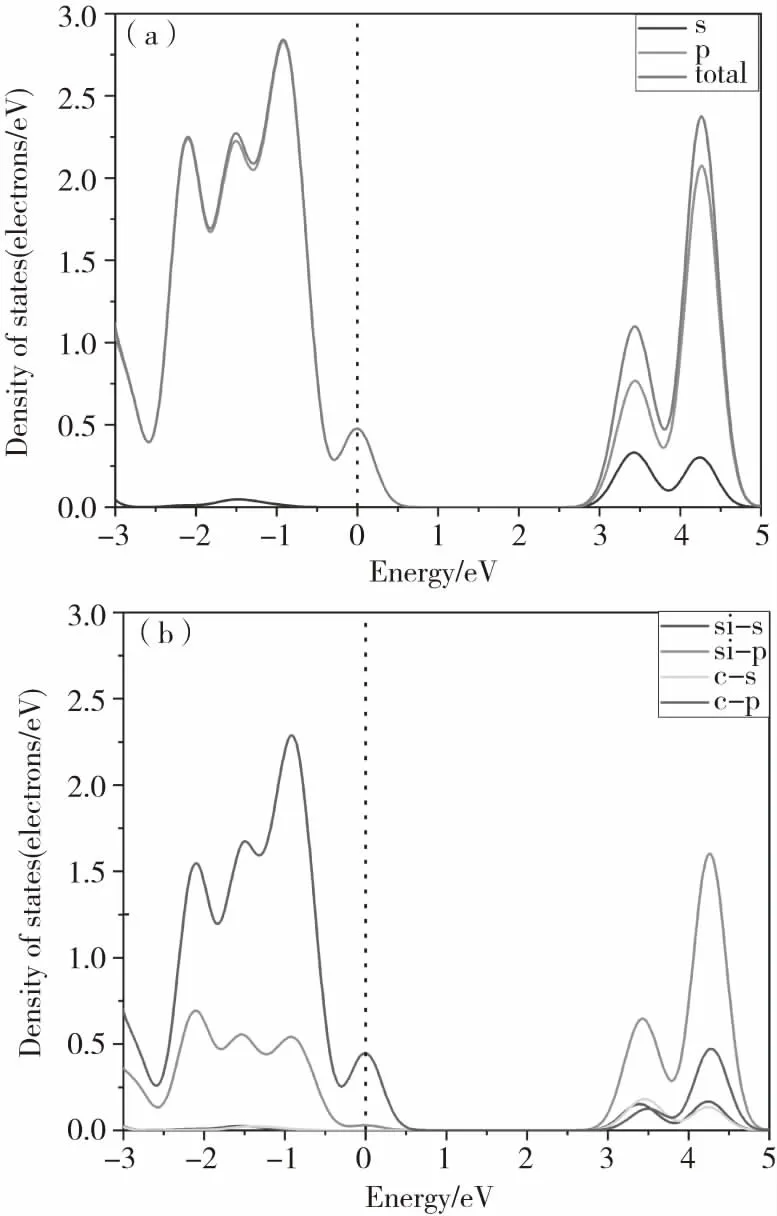
图2 4H-SiC完美薄膜下的DOS

3.2 硅原子空位的态密度图

本文所计算的硅原子空位的缺陷浓度为2.3×1021cm-3.从图3(a)中可得出当引入硅原子空位后态密度向左偏移，说明费米能级在禁带中偏向能量较高的导带，当有硅原子空位产生时，与之相邻的碳原子会产生悬空键，从图3(b)中可得出碳原子的电子能级在硅空位缺陷中比完美碳化硅晶体中更加活跃。在0.94 eV到1.96 eV范围内硅原子空位的DOS等于0，这表示在硅原子空位下4H-SiC薄膜的禁带宽度为1.02 eV，与完美薄膜2.28 eV相比较明显减小，这说明硅空位的产生会减小禁带宽度，从而导致硅空位缺陷的导电性能增加。

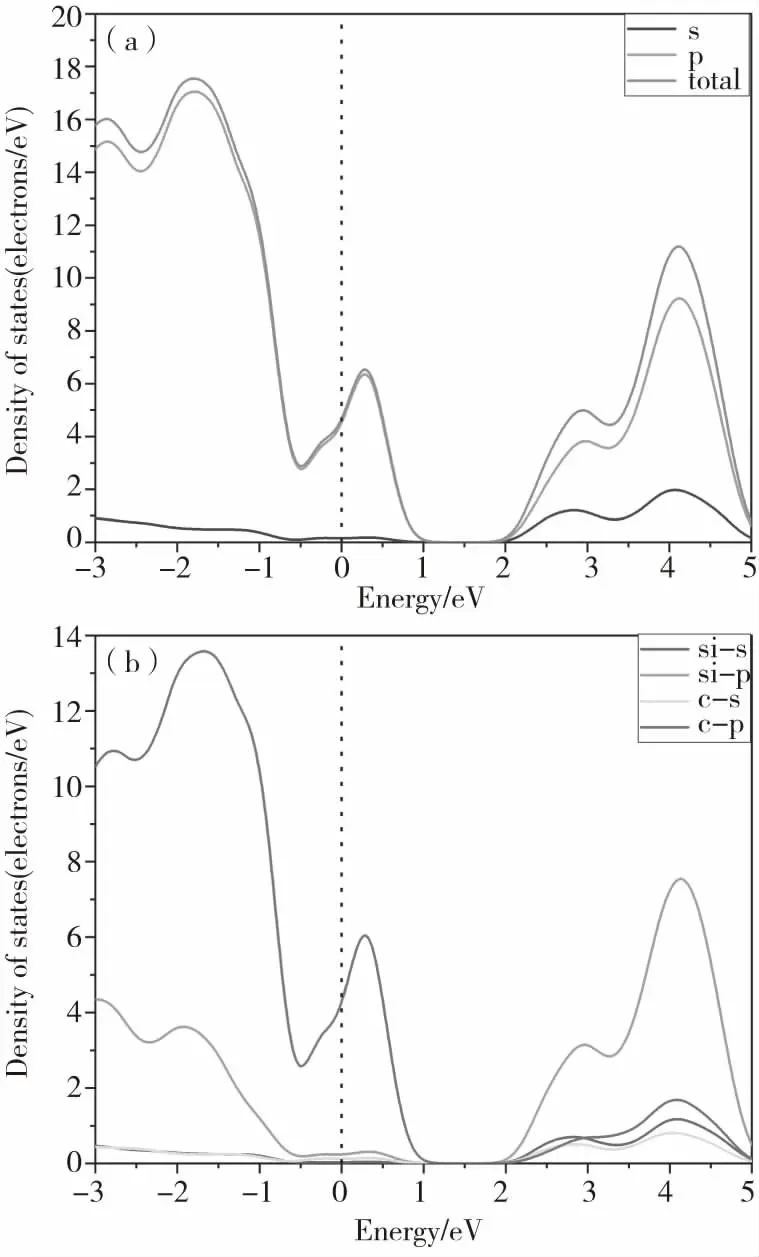
图3 4H-SiC中硅原子空位缺陷的DOS

3.3 碳原子空位的态密度图

本文所计算的碳原子空位的缺陷浓度为2.4×1021cm-3.当有碳原子空位产生时导致与之相邻的硅原子产生悬空键，从图4(a)中可得出在0.51 eV到0.79 eV范围内产生了一个新的峰值。这说明当碳原子缺失态密度发生变化，从而改变了碳化硅材料的某些特性。从图4(b)中可进一步看出当缺少碳原子对硅原子的约束后，硅原子的作用效果进一步加强。通过对图3、图4比较可得出碳原子空位的能带宽度小于硅原子空位的能带宽度，这说明在碳化硅材料生产过程中碳原子空位的导电性要优于硅原子空位的导电性。

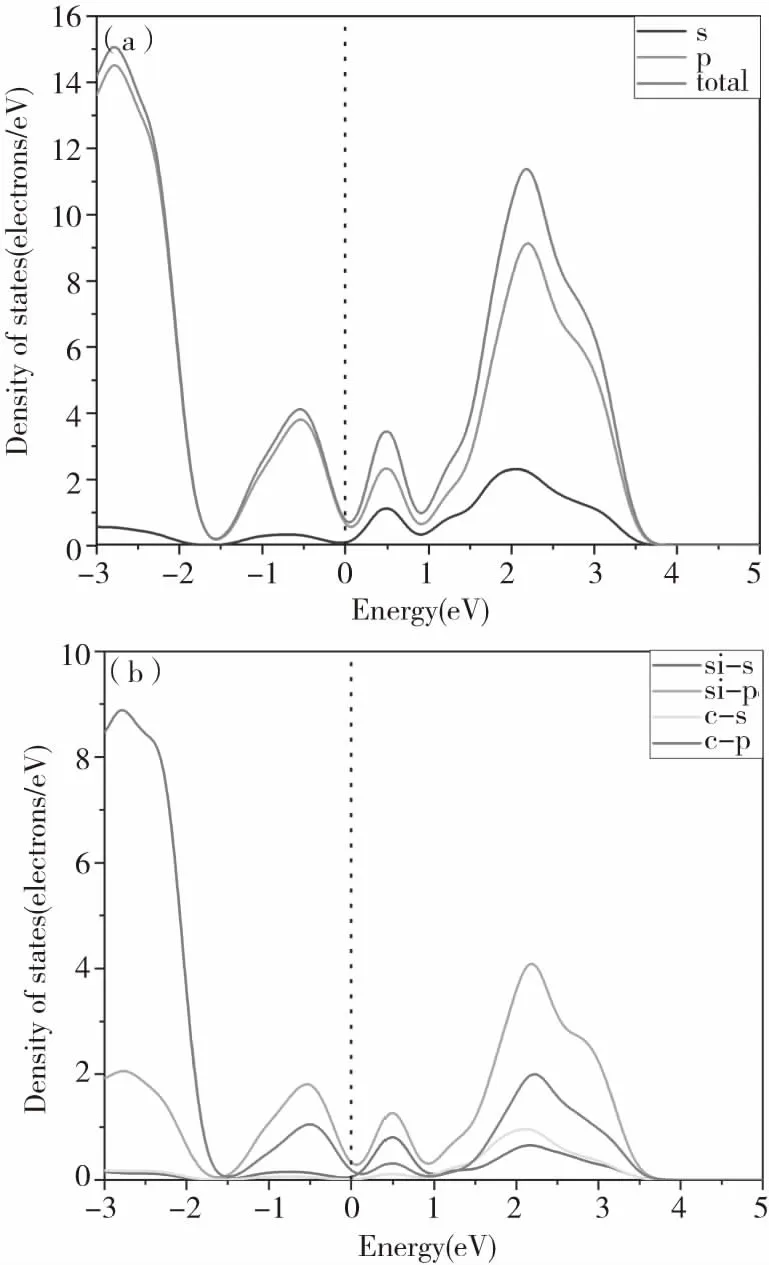
图4 4H-SiC中碳原子空位缺陷的DOS

4 掺杂原子替换缺陷下的态密度图

4.1 硼原子掺杂的态密度图

本文所计算的硼原子替换硅原子后的掺杂浓度为2.38×1021cm-3.硼原子替换碳原子后的掺杂浓度为2.32×1021cm-3.从图5(a)中可得出当硼原子替换硅原子后0.45 eV到2.04 eV范围内DOS等于0则禁带宽度为1.59 eV，图5(c)中硼原子替换碳原子后0.72 eV到2.07 eV范围内DOS等于0则禁带宽度为1.35 eV.所以硼原子替换硅原子后产生的禁带宽度要大于硼原子替换碳原子产生的禁带宽度，从图5(b)(d)中可得出当引入硼原子掺杂后在价带区域碳原子的DOS对总的DOS有较大的作用，在导带区域硅原子的DOS有较大的作用。硼原子的电子能级强度在硼原子替换碳原子的条件下更明显。当硼原子掺杂后整体曲线右移，费米能级靠近价带区域，这说明将硼原子引入后4H-SiC半导体为P型半导体。

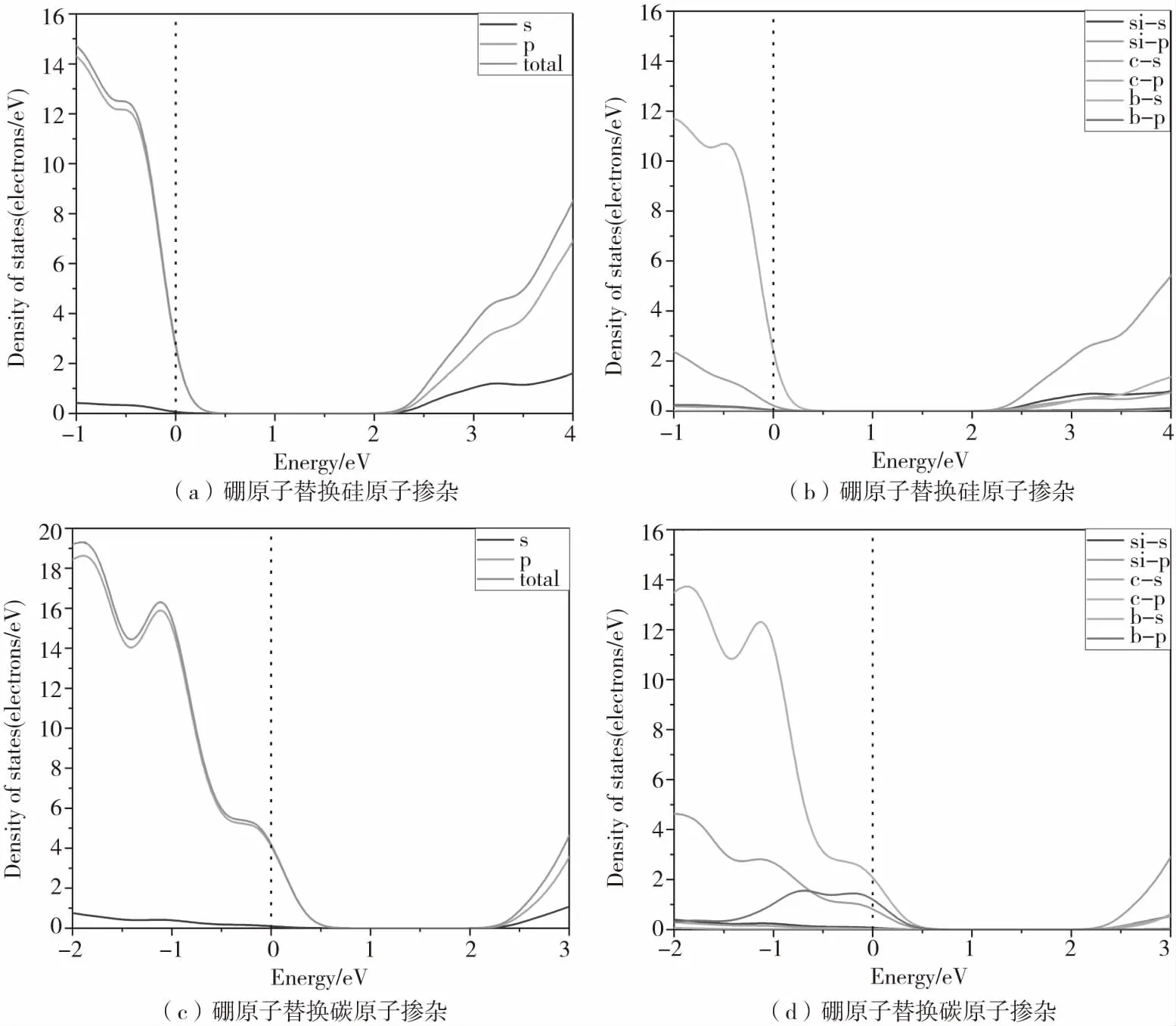
图5 硼原子掺杂

4.2 磷原子掺杂的态密度图

本文所计算的磷原子替换硅原子后的掺杂浓度为2.31×1021cm-3.磷原子替换碳原子后的掺杂浓度为2.34×1021cm-3.从图6(a)中可得出当磷原子替换硅原子后在-2.42eV到-0.6 eV范围内DOS等于零，则禁带宽度为1.82 eV;从图6(c)中得出当磷原子替换碳原子后在-2.36 eV到-0.65 eV范围内DOS等于零，禁带宽度为1.71 eV因此可得出磷原子替换硅原子后的禁带宽度要大于磷原子替换碳原子的禁带宽度。磷原子替换碳原子后的导电性更好。从图6(b)(d)中可得出当引入磷原子掺杂后在价带区域碳原子的DOS对总的DOS有较大的作用，在导带区域硅原子的DOS有较大的作用。磷原子的电子能级强度在磷原子替换碳原子的条件下更明显。当磷原子掺杂后整体曲线左移，费米能级靠近导带区域，这说明将磷原子引入后4H-SiC半导体为N型半导体。

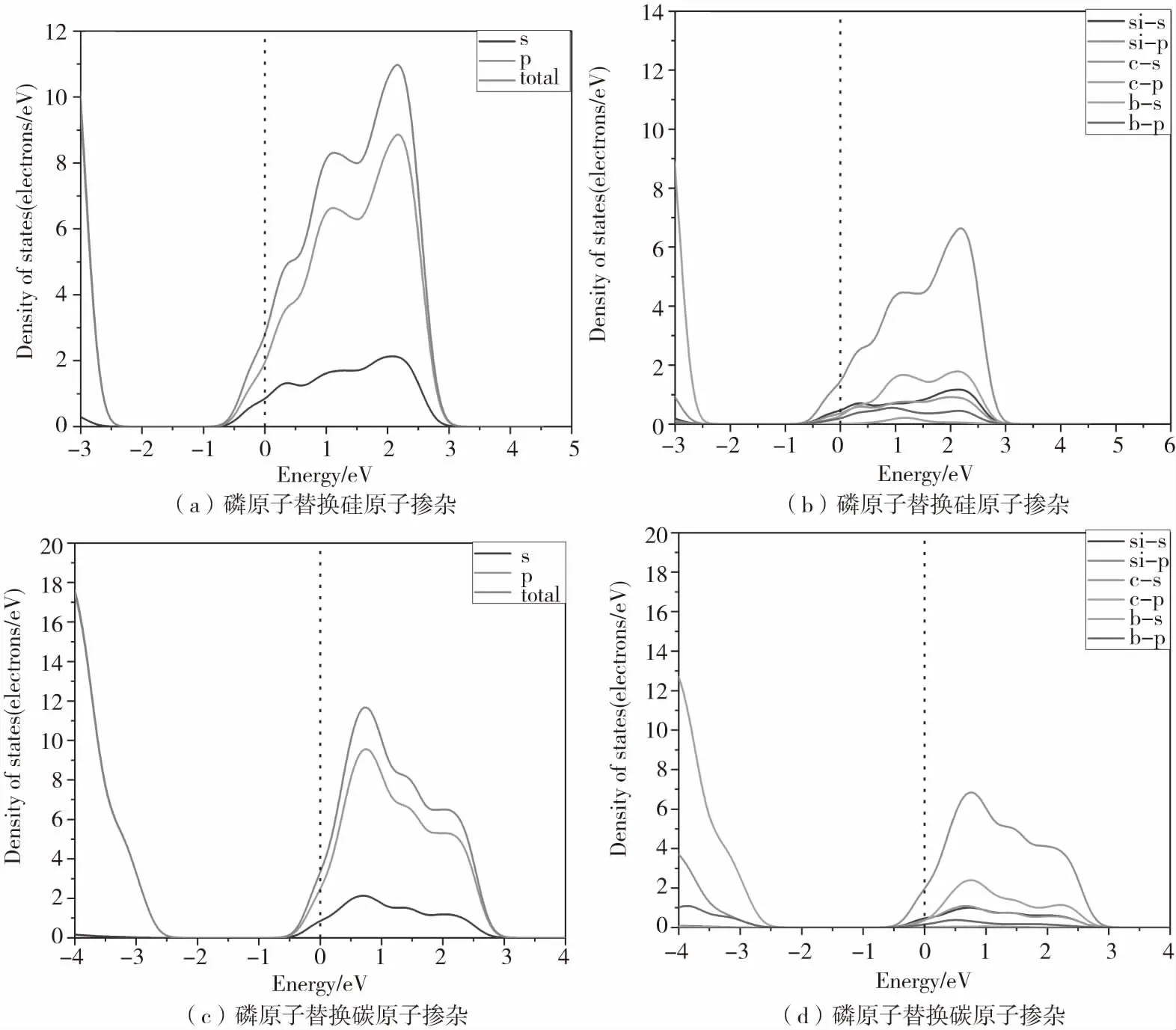
图6 磷原子掺杂

5 结论

通过第一性原理计算得出在碳化硅材料的各种缺陷中碳原子空位缺陷产生的禁带宽度最小，磷原子替换硅原子后产生的禁带宽度最大。这说明碳原子空位缺陷的碳化硅半导体材料的导电性要好，磷原子替位缺陷的碳化硅半导体材料更适用于宽禁带材料。硼原子掺杂使得4H-SiC呈现P型半导体的特性，磷原子掺杂使4H-SiC呈现N型半导体的特性，且硼原子掺杂后半导体的导电性要优于磷原子掺杂。在4H-SiC半导体中导带底和价带顶主要由Si 3p和C 2p能级决定，这也就决定了4H-SiC半导体的带隙主要由Si原子和C原子的电子状态决定。在碳空位缺陷的情况下会产生新的峰值，这表明缺少碳原子对硅原子的约束后硅原子的电子活跃程度更强。对缺陷的形成能进行比较可得出碳原子空位的形成能要小于硅原子空位的形成能，所以在半导体生产过程中碳原子空位缺陷比硅原子空位缺陷更容易形成。同时可得出原子空位缺陷比原子掺杂缺陷更容易形成。