基于灰色-马尔科夫模型的桥梁运行状况预测

贾庆林，韩智强，晋民杰，李路遥，李华腾

(太原科技大学 交通与物流学院，太原 030024)

随着桥梁服役时间的增加，车辆行驶、风荷载等因素对桥梁运行状况造成显著影响。因此，开展桥梁运行状况的预测研究对后续安全检查有着重要的意义。

近年来，灰色系统模型和灰色-马尔科夫模型是进行预测较为精准的算法，国内外相关学者在该领域开展了大量的研究。Hang Jiang等运用灰色模型对我国的直接投资进行预测，并结合残差进行修正，以提高其精度[1]；裴彧等提出新陈代谢法与残差修正来优化灰色马尔科夫模型，并对桥梁状态进行预测[2]；哈娜和付深远采用三弯矩法对其原始数据进行处理，并在此基础上，运用灰色-马尔科夫组合模型和回归方程对桥梁耐久性进行精确预测，消除了传统预测模型无法考虑不确定因素的影响[3]；Dengji Zhou等建立马尔科夫-灰色关联度的新型模型，并对该模型的参数和预测准确性进行分析，得出最佳的参数和预测结果[4]。

基于上述研究成果，可以看出运用灰色系统模型和灰色马尔科夫模型进行预测，精度颇高，其函数的走向和趋势也与原始数据非常接近，但是一些不规则因子的影响，导致其预测结果可能与其真实值有些波动。因此，本文提出一种灰色-马尔科夫模型，并在此基础上结合曲线拟合进行修正，使用MATLAB数值处理软件进行模型计算，并通过案例分析，与桥梁实际状况，进行对比，验证该方法的实用性和可行性。

1 灰色-马尔科夫模型与曲线拟合

1.1 灰色系统模型

灰色系统模型就是应用不足的、不完整的数据，对事物的发展状况进行预测。

1)灰色系统模型的基本公式，如式(1)所示[5]。

k=2,3,…,n

(1)

式中：x(0)为模型的灰导数；a为模型的发展系数。b为模型的灰作用量。

2)灰色系统模型的矩阵算式如式(2)～式(4)所示[6]。

(2)

Y=[x(0)(2),x(0)(3),x(0)(4),…,x(0)(n)]T

(3)

(4)

由上式(4)计算出a和u，并得到灰色系统模型的时间响应函数，如式(5)所示[7]。

k=1,2,…

(5)

由公式(5)进行还原，得到实际数据模拟序列函数，如式6所示[8]。

k=1,2,…

(6)

公式(6)可以准确地反映原始数列的变化趋势、增长(减少)趋势。当k取1,2,…时，可以求出数据的训练值，当k大于等于n时，可以求得数据的预测值。

1.2 马尔科夫模型

马尔科夫模型属于随机数学模型，该模型主要记录预测目标在不同时间中所处的状态。

1)根据灰色系统模型，计算模型的残差和相对误差，如式7所示。

(7)

式中：t为每一时刻。

2)根据相对误差的大小，对数据进行划分状态。

Ei=[E1,E2…Er]，Er=[Δ1(t)…Δ2(t)]

(8)

划分状态就是将相对误差按照实际情况平均划分为若干区间，在根据这些区间，划分出各变量的工作状态[9]。

按照各变量的工作状态，将灰色系统模型的训练值进行修正，如式9所示。

(9)

3)计算状态转移矩阵P，首先得出k步状态转移概率Pij(k)，其中Pij(k)表示第一个状态Ei转移到另一个状态Ej的概率[10-12]。

(10)

(11)

式中：k为状态的数目；mij为状态Ei经过k步转移到Ej的数量；mi为状态Ei的数量。

4)根据状态转移矩阵P计算出预测年份的各个状态所占的比重，在用加权平均法计算出预测值。

(12)

1.3 最小二乘法曲线拟合

最小二乘法曲线拟合较好的消除数据一些不规则因子的影响，并对灰色-马尔科夫预测模型结果进行修正，以达到符合现实要求的效果。

设年份为自变量t，桥梁的工作状态评分分数F为因变量，用n次多项式进行拟合，p为相关系数，则对应函数关系表达式[13-14]，如式13所示。

F=p1nt+p2tn-1+…+pnt+pn+1

(13)

根据灰色-马尔科夫模型与曲线拟合的相关理论，首先对桥梁的原始数据，运用灰色系统模型进行初步预测，在此基础上，使用马尔科夫模型进行修正，之后，对得到的预测值用最小二乘法曲线拟合进行修正；其次，就是精度验证，结果对比；最后得出结论。该流程如图1所示。

图1 灰色-马尔科夫模型预测的流程图

2 案例分析

2.1 数据来源

数据是采用2007-2016年河北省某地区的159座桥梁的安全检测样本[15]，如表1所示。

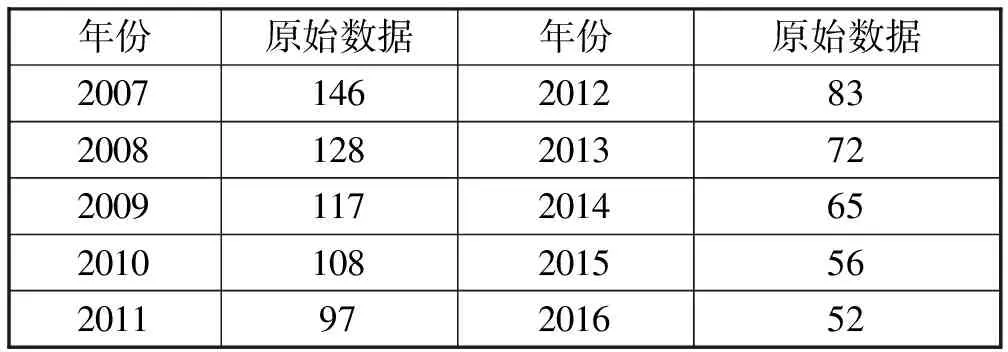
表1 2007-2016年的桥梁安全检测样本

2.2 灰色系统模型预测

使用桥梁运行状况的原始数据，建立灰色系统模型，并通过灰色系统建模软件GTMS3.0的应用，得到灰色预测值[16]，即利用2007-2014年的原始数据来预测2015-2016年的桥梁运行状况，其预测值分别为59.5231、53.1926，并运用公式(6)，得出2007-2014年的训练值，如表2所示。

表2 2007-2014年的训练值

2.3 马尔科夫模型修正

1)根据上述结果，运用公式(7)，得出残差值和相对误差值，并如图2，图3所示。

图2 残差折线图

由图3可知，桥梁运行状况的相对误差区间为-3.52%～3.78%.

图3 相对误差折线图

2)根据桥梁运行状况的相对误差，按照公式(8)，可以将其划分为三个状态区间，并介于-3.52%～3.78%，详细如表3所示。

表3 马尔科夫模型的状态划分

按照马尔科夫模型的状态划分标准，对桥梁2007～2014年的运行状况进行划分，并根据公式(9)算出2007-2014年的训练值修正，如表4所示。

表4 桥梁工作状况的划分以及训练值修正

3)根据表4以及公式(10)和公式(11)，得到转移矩阵P(1)，由于高次方使得马尔科夫预测更加精确，所以本文进行四次方和五次方，如P(2)和P(3)所示。

4)由表4得知，2014年桥梁的运行状况处于E1，令其v0等于(1,0,0)，进而可以预测出2015年和2016年的运行状况，见表5.

表5 运行状况的预测数据表

从表5可以得出2015年的运行状况处于E1，2016年也处于E1，再由式(12)以及加权平均法，得到2015年的预测值为58.573 5，2016年的预测值为53.007 8.

2.4 最小二乘法曲线拟合修正

将马尔科夫修正值和原始数据进行最小二乘法曲线拟合。根据公式(13)，原始数据为因变量，马尔科夫修正值为自变量，建立二次多项式方程[17]。

y=-0.000 550 3x2+1.119x-6.087，拟合方差为2.097，相关系数为0.999 6，调整后相关系数为0.999 5，均方差为0.647 7，拟合曲线如图4.

图4 方程的曲线拟合图

从图4中，可以看出曲线拟合的误差极小，证明其拟合的效果极佳。将马尔科夫修正的预测值代入方程中，得到2015年的预测值为57.568 7，2016年预测值为51.682 5.

3 预测精度

本文运用后残差法进行检验其预测精度，等级划分标准[18]见表6.

表6 检验精度等级划分表

根据已知数据，计算得知，在预测桥梁的运行状况中，2014年和2015年原始数据的均值为54，原始值与预测值的误差均值为0.9431，原始数据的标准差S1为2，原始值与预测值的误差标准差S2为0.625 6.

计算方差比：

从表6中查询可知，该预测模型的精度等级达到了一级标准，所以可以用于预测桥梁的运行状况。

4 结果对比

为了验证本次预测模型的有效性和可行性，将曲线拟合修正的预测数据与单纯使用灰色模型的预测数据以及马尔科夫模型修正的预测数据进行对比。

从表7可以看出，原始数据经灰色系统模型预测后，再经过马尔科夫模型修正以及曲线拟合修正后，所预测出来的数据的平均误差极小，其预测准确度较高。

表7 三种预测方法的结果对比表

由于桥梁的运行状况中，预测值的单位为座，所以2015年预测值为58座，2016年为52座。

5 结论

1)本文是以河北省某地区159座桥梁的运行状况为依托数据，运用灰色系统模型、马尔科夫模型以及最小二乘法曲线拟合，对2015年、2016年的运行状况进行预测，并与原始值作对比。

2)通过模型预测，采用灰色系统模型，其相对误差在2.29%～6.34%；采用马尔科夫模型修正，其相对误差在1.94%～4.60%；采用灰色-马尔科夫和最小二乘法组合模型，其相对误差0.61%～2.80%，误差为最小。其结果满足工程需求，同时研究结果对桥梁运行状态的预测有一定的参考意义。