基于误差阈值控制的ICP点云配准算法研究

张晶，叶含笑，杨麟

（1.中国美术学院，杭州 310002；2.浙江中医药大学，杭州 310053）

一、背景

文物是由人类创造的在社会文明发展过程中保存下来的具有历史、人文、艺术和科考研究价值的宝贵遗迹。绝大部分文物在时间沉淀中会自然风化或被人为损坏。文物修复在考古和文物研究中是最为关键的、技术性极强的工作，很多抢救性的文物修复往往任务繁重，时间紧迫。通过虚拟复原技术不仅可以降低传统文物修复的难度，减少贸然修复过程中的人为因素对文物的损坏，数字化文物虚拟复原的模型还可应用于虚拟博物馆的数字化文物展，通过互联网技术实现文物资源共享，从而极大提高科考等的工作效率。因此文物数字图像三维虚拟修复具有极大的技术研究价值，同时具有重要的应用研究及社会人文价值。

二、点云数据采集

点云数据采集可以通过数码相机或激光扫描获得，数码相机主要用来测量点的三维坐标和颜色信息。移动激光扫描系统一般由激光扫描仪和导航系统组成，移动激光扫描系统主要用于测量点的三维坐标和点的激光反射强度；根据数码相机和移动激光扫描系统采集的数据可以得到点云数据，通过这种方式采集到的点云包含颜色信息、激光反射强度和三维坐标。通常点的三维坐标属于本地坐标系中的坐标。

通过对文物进行全息记录和转化可以将文物以数字化形式保留下来，文物数字化可以抢救性地记录和保全文物信息，为文物展示、研究等的应用提供取之不尽用之不竭的数字化信息。本文涉及的文物数字化信息通过三维激光扫描获得，未经过其他处理手段，三维扫描获得的点不仅包含了三维坐标的信息，同时也包含了颜色、光照反射强度值、分类值、时间等的信息，像素点的颜色信息首先通过相机获取，同时将像素的颜色信息（RGB）赋予坐标位置上对应点云中的点上。光照反射强度信息由激光扫描仪接收装置所获取，此强度信息与文物表面的材质、粗糙程度、入射角的方向，以及发射光的强度、激光波长有关。对于复杂三维外形，其坐标轴之间并没有被以某种规律或某种数值关系确定下来，所以采集到的点无法建立纵横坐标之间的联系，点云配准就是为了把不同坐标系中的点云映射到相同坐标系中，因此点云配准在计算机视觉辅助工程应用中具有重要作用，也是计算机视觉研究的关键问题之一，如逆向工程、同步定位与建图、图像处理和模式识别等。

三、文物扫描数据点云配准

点云配准（Point Cloud Registration，PCR）过程就是指通过求两个点云之间的旋转变换和平移变换（Euclidean Transform and Rigid Transform），将处于不同视角下获得的点云整合到指定坐标系下的过程。具体可以描述为：由于间断扫描或移动扫描，使得完整的文物数据信息处在了不同坐标系上，从而导致对应的两组点云出现，把原点云Ps（Source Cloud）和目标点云Pt（Target Cloud）通过旋转变换，组合到相同的坐标系下，再通过位移矩阵T，使得Ps和Pt的重合达到尽可能最优。变换矩阵可以是刚性的（Rigid），也可以不是刚性的，本文只考虑刚性变换，即点云变换只包括平移、旋转。刚性点云配准可以被分为粗略配准（Coarse Registration）和精细配准（Fine Registration）两个步骤。粗略配准指的是在两幅不同坐标系上点云之间的变换在完全未知的情况下进行较为粗略的配准，可以被看作是为精配准提供预处理的初值变换；精配准则是根据在粗略配准基础上给定的一个初始变换，进一步优化后得到更为精确的变换。

对于静态场景，目前应用最为广泛的点云精准配准算法依然是迭代最近点算法（Iterative Closest Point，ICP），本算法由Besl and McKay 1992年在A Method for Registration of 3-D Shapes文章中最先提出，以及ICP 算法的各种变种算法，比如point to plane ICP、稳健ICP、Point to line ICP、NICP、MBICP和GICP等。

四、ICP算法描述

三维文物扫描点云配准为了将不在同一坐标系下的两组或多组点云通过点云的旋转和平移变换统一到同一参考坐标系下。这个变换过程，可以通过映射操作来完成。要得到精确值在现实中是难以实现的，因此为了获得精确的点云配准，通常情况下，会尽可能多的寻找被匹配的对应点对，以便尽可能地提高变换矩阵预设参数的精度。

图1为文物三维扫描传统的ICP算法点云配准三维重建效果图，由图可以看出重建后的文物产生了部分倾斜。

图1 I CP算法点云配准三维重建效果图

五、ICP算法的原理与计算步骤

传统ICP算法的基本原理就是在拟匹配的目标点云Q和源点云P中，分别按照预先设置的约束条件，找到最邻近的点（pi，qi），最后计算出源点云和目标点云点对的最优匹配参数R和T，并且要让点对之间的误差函数最小。假定点对之间的误差函数用E（R，T）表示，其计算表达式如公式（1）所示：

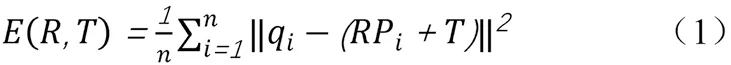
公式中qi为目标点云Q中与原点云中的一点pi对应的最近点，pi即为原点云P中的一点，n表示最邻近点对的数量，R为旋转矩阵，T为平移向量。

（一）ICP算法的计算步骤

1.取点pi∈P，P为源点云集；

2.通过计算，寻找对应点qi∈Q，Q为目标点云，使得||qi-pi||=min；

3.计算平移矩阵T和旋转矩阵R，使得误差函数的值最小；

4.根据上一步求得的平移矩阵T和旋转矩阵R，对pi进行平移和旋转变换，获得新的对应点集

5.计算对应点集qi与新的对应点的平均距离；

6.如果d大于预设的最大迭代次数或者小于预先给定的阈值，则停止迭代计算。如果不满足以上条件，则返回第2步计算，直到满足收敛。

（二）ICP算法的关键

1.原始点集的采集手段，采集的具体方法有：均匀采样、随机采样和法矢采样。

2.确定对应点集：点到点、点到投影、点到面。

3.计算变化矩阵，具体包括：四元数法、SVD奇异值分解法

六、基于误差阈值控制的ICP优化算法

ICP算法点集P{Pi,i=1,2,…,N}表示空间第一个点集，目标点集Q的坐标为为在第k次迭代中，计算与源点集P坐标中相对应的点的坐标，设计并计算P与Qk之间的变换矩阵，并对原变换矩阵进行更新，直到源点与目标点的数据间平均距离小于给定值τ。算法的关键是求解P与Qk之间的变换矩阵，即求R，T两个矩阵，满足误差函数式（2）最小：

这种算法是合理的，因为总体点集误差的倍数应该小于不匹配部分的

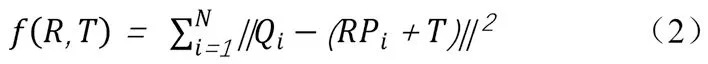
容许误差倍数，即总体上的误差控制要严格，局部点集的误差控制可以比较大。因为在实际的配准问题中，确实会存在部分点完全无法匹配的情况，此时局部点集的误差会很大。而本优化算法可大大节约循环次数，减少运算代价。图2为基于误差阈值控制的ICP算法点云配准三维重建效果图。

图2 I CP优化算法点云配准三维重建效果图

说明在上述的容许误差倍数下，不匹配点占总点数的比率小于等于25%才能获得能接受的配准效果。显然，t越大，即总体配准的接受容许度越大，比率越大，越能容许更多的不匹配点；K越大，即不匹配点的误差很大，则比率越小，只能容许较少的不匹配点。

七、结果

利用三维扫描仪获得文物点云数据，利用 ICP 算法进行初步配准，得到初始模型，由图1发现重建后的数字化文物出现了变形效果。对 ICP 算法通过误差阈值控制等方法进行优化后，在实验中发现优化后的算法文物的配准速度和精度都得到大幅度提升。实验结果表明ICP 算法要获得最优效果，还有很长的路可走，可进行多种优化，ICP算法优化后获得的三维模型比三维扫描仪自带的点云自动配准软件获得的模型更加精确。