频域反射法中阻抗变化类型判断技术
2021-08-28饶显杰黄永禄李明志
饶显杰 周 凯 黄永禄 李明志 李 蓉
频域反射法中阻抗变化类型判断技术
饶显杰 周 凯 黄永禄 李明志 李 蓉
(四川大学电气工程学院 成都 610065)
利用行波的反射可以有效地探测电缆的局部缺陷和故障等阻抗异变点,反射波的传播距离和极性可分别用于定位阻抗异变点和判断阻抗异变点的类型。频域反射(FDR)技术是识别电缆中反射波的有效手段之一,但是现有FDR技术仅能计算反射波的传播距离,而不能判断波形极性,因此,该文提出一种FDR的波形极性判断技术。首先阐述FDR中反射波的识别原理,将Hanning自卷积窗的快速傅里叶变换插值算法用于FDR中反射系数谱分析,对FDR测试下限频率和频变波速造成的相位偏差进行修正,得到频率值和修正后的相位值用于计算反射波的传播距离和判断波形极性;然后对单反射波和多反射波的电缆模型进行仿真,检验该技术的可行性;最后在实验室105m长的10kV交联聚乙烯电力电缆上制作阻抗异变点对该方法的准确性进行验证。仿真和实验结果表明,该文所提方法可以有效获取FDR中反射波的传播距离和极性。
频域反射 反射波 极性判断 Hanning自卷积窗 相位修正
0 引言
近年来,伴随着我国城市的高速扩张和发展,城市用电量逐年攀升,对城市配电网的供电可靠性提出了更高的要求[1-2]。为了满足城市发展的需求,交联聚乙烯电力电缆开始逐渐在城市配电网的输电系统中占据主导地位[3-4]。恶劣复杂的服役环境和错误的施工操作可能破坏电力电缆,迫使其出现局部缺陷,随着服役年限的增加,局部缺陷可能会演变为故障,导致城市电网意外性停电事故,造成经济损失[5-6]。因此电缆中缺陷或故障的主动定位探测技术极具研究意义。
电缆中局部缺陷或故障会迫使电缆局部特性阻抗发生异常变化,产生阻抗异变点,同时阻抗异变点会引起行波在该位置的反射现象,因此大量学者通过研究反射波的识别技术来探测电缆的阻抗异变点。其中,反射波的传播距离可用于定位阻抗异变点;反射波的极性可用于判断阻抗异变点的类型[7]。
时域反射(Time Domain Reflectometry, TDR)技术[8-9]在电缆首端位置注入脉冲信号,然后直接在时域中识别反射波形,由于该方法可以直观地得到反射波的传播距离和极性,因此被广泛用于电缆中反射波的识别。但是该方法受环境噪声影响大,同时该方法中脉冲信号的高频能量少而且高频能量在电缆中衰减明显,因此,TDR难以识别微弱反射波。文献[10]在TDR基础上提出了扩展频谱时域反射法,该方法利用单频点的反射信息结合互相关算法完成反射波的识别,提高了传统TDR方法的抗噪能力,但是该方法的频域信息过少,因此也难以识别微弱反射波。
频域反射(Frequency Domain Reflectometry, FDR)技术[11-12]中信号高频能量更多,频域信息丰富,能够识别更加微弱的反射波,因此逐渐取代了TDR技术。该方法采用扫频信号对电缆首端进行测试,然后通过特定算法进行时频等效变换,最后完成反射波的识别。文献[13]提出将FDR中宽频阻抗谱借助积分变换来识别电缆中反射波,并取得较好的识别效果,但是该方法要求被测电缆正常时的多组原始数据,因此工程上的实用性较差。文献[14-15]提出利用快速傅里叶反变换处理阻抗谱数据完成反射波识别,但是该方法要求扫频信号的上限频率更高,同时采集点数也要求更多,因此测试成本较高;另一方面,测试频率过高时测量夹具和电力电缆的连接效果将严重影响测试结果。文献[16]提出将FDR中反射系数谱在加Kaiser窗后进行离散傅里叶变换实现微弱反射波的识别,该方法对测试频带和采集点数的要求不高,同时不需要被测电缆完好时的测试数据,因此具有更好的应用前景,但是该方法存在参数难以确定和计算效率低的问题。另一方面,目前基于FDR的研究仅能计算反射波的传播距离,即定位阻抗异变点,而无法确定反射波的极性,即无法确定阻抗异变点的类型。
综上所述,本文在前人研究的基础上提出一种频域反射的波形极性判断技术,该方法可以利用FDR中反射系数谱确定反射波的传播距离和极性,进而定位阻抗异变点和判断阻抗异变点的类型。本文首先介绍了FDR的反射波识别原理,将FDR中反射波的传播距离计算问题和极性判断问题转化为周期分量的频率和相位估计问题;接着将Hanning自卷积窗(Hanning Self-Convolution Windows, HSCW)的快速傅里叶变换(Fast Fourier Transform, FFT)插值算法用于估计周期分量的频率和相位,以解决原有算法中参数难以确定和计算效率低的问题,估计的频率值可直接用于计算反射波的传播距离;最后考虑FDR测试下限频率和频变波速的影响,对估计的相位值进行修正,利用修正后相位值确定反射波的极性。仿真和实验验证了该方法的可行性与有效性。
1 FDR的反射波识别原理
1.1 传输线基本理论
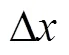




式中,为角频率,f为信号的频率;rc为缆心的半径;rs为金属屏蔽层的半径;为缆心的电阻率;为金属屏蔽层的电阻率;为真空磁导率;为交联聚乙烯的电导率;e 为交联聚乙烯的介电常数。
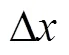


其中
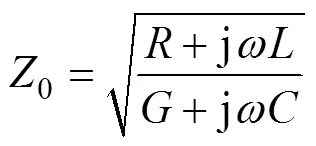
式中,Z为距电缆首端处的等效阻抗;0为特性阻抗。
当传输信号的频率较高时,0为
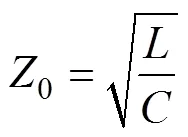
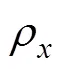
1.2 反射波的传播距离计算原理


图2 反射系数与负载阻抗关系

图3 反射波传播示意图


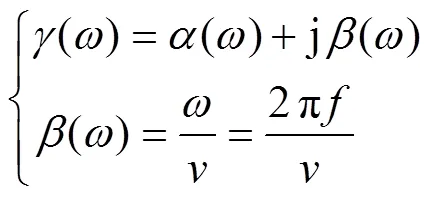
将式(11)代入式(9)得到
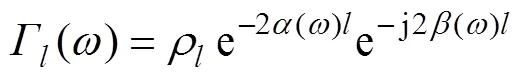
借助欧拉公式分解式(12)得到

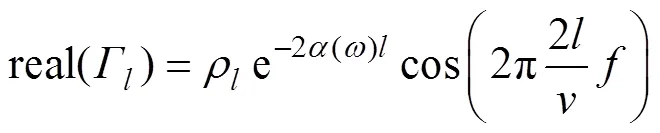
观察式(14)可知,当注入行波为高频信号时,将看作自变量,反射系数实部中产生了频率为2/的等效周期分量,且该频率的数值正好为行波传播2所需时间的数值。该周期分量是由电缆末端的反射现象产生的,因此该周期分量对应电缆末端的反射波,即图3中的反射波P。
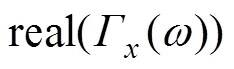
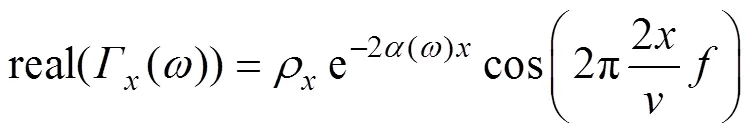
观察式(15)可知,对应的等效周期分量的频率为2/,该频率的数值正好为行波传播2所需时间的数值。以此类推,当FDR测试结果中存在多个反射波时,可以通过对反射系数实部中各等效周期分量进行频率估计来确定FDR中各反射波的传播距离。
1.3 反射波的极性判断原理
目前已有的FDR方法仅能计算反射波的传播距离,借此确定阻抗异变点位置,但是无法判断FDR中反射波极性,即无法确定阻抗异变点类型,由此本文侧重于研究FDR中反射波极性判断技术。
利用图2改写式(15),得到

需要说明的是,当=0时,此时电缆距首端处没有阻抗异变点,该位置不存在反射信号,因此本文不对该情况进行讨论。对式(16)利用三角函数变换公式进行进一步改写,得到
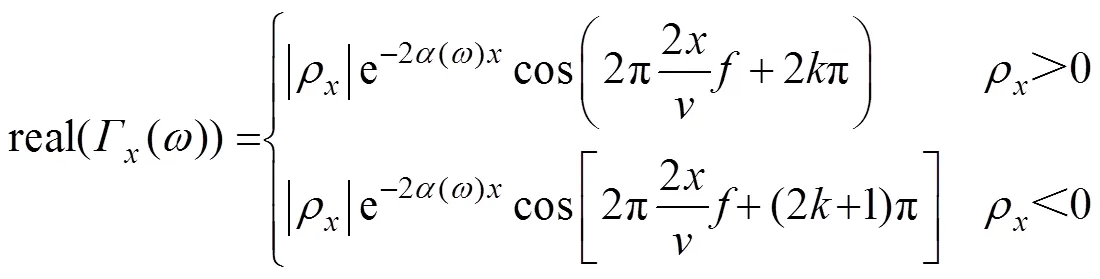
式中,为整数。
综上所述,借助反射系数谱的实部,FDR中反射波的传播距离计算问题和极性的判断问题转化为周期分量的频率和相位估计问题。
在实际工程中进行FDR测试时,综合考虑测试的成本和效率后,会设定一个测试下限频率min和测试上限频率max,同时为了准确地识别FDR中各反射波,FDR的测试频率间隔s应满足奈奎斯特采样准则,如式(18)所示,保证其能有效测试到电缆末端的反射信号。

2 Hanning自卷积窗的FFT插值算法
本文采用傅里叶变换算法分析反射系数实部的周期分量,由于实际采集的信号存在非同步采样和数据截断的现象,用傅里叶变换算法进行周期分量识别时会产生频谱泄漏和栅栏效应[21],影响FDR中反射波的辨识能力。因此需要进行离散频谱的校正,本文采用FFT插值[22]的方法来校正离散频谱,该方法可以在频谱上增加数据的频率分辨率,进而提高周期分量的频率和相位计算精度。对FDR中反射波的识别而言,该方法可以在有效的测试频带中,更好地确定反射波形的特征。同时借助FFT插值算法可以有效提升计算效率。
由于本文需要精确估计反射系数实部中各周期分量的频率和相位,且要提升对微弱反射波的识别能力,因此需降低各周期分量的谱间干扰。当增加卷积阶数时,Hanning自卷积窗[23]的旁瓣衰减速率快速增加,此时各周期分量的相互干扰能够得到有效抑制,频谱泄漏现象得到改善。因此本文利用该技术处理反射系数谱以获得更好的反射波识别效果。
Hanning窗离散形式下可表示[23]为

式中,为Hanning窗的窗长。
把个Hanning窗自卷积得到阶HSCW为

当构造窗长为的阶HSCW时,各Hanning窗的为

式中,floor为向下取整。
利用式(20)和式(21)构造HSCW后,在序列末尾补零便得到阶HSCW。图4展示了=126的1~3阶HSCW幅频响应曲线,当卷积阶数增加时,HSCW的旁瓣电平在减小,旁瓣衰减速率在增加,这说明HSCW可以有效抑制频谱泄漏,减少谱间干扰,因此将其用于反射系数谱处理有助于精确估计各周期分量的频率和相位。当选取太大时,不仅计算复杂,同时主瓣宽度会过大,不适合频谱密集情况下的识别,因此本文采用2阶HSCW,以解决原有Kaiser窗[16]中需要确定参数的难题。

图4 HSCW的旁瓣性能

3 FDR的波形极性判断技术

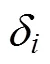
3.1 FDR测试下限频率的相位修正
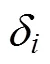



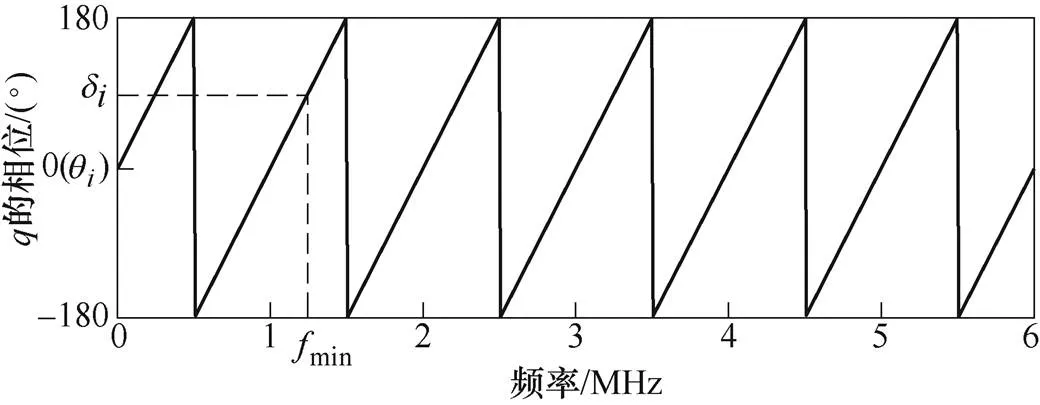
图5 q的相位函数波形
3.2 频变波速的相位修正
当传输信号的频率变化时,电缆单位长度的电容、电感参数值会产生不同程度的变化,导致不同频率的波速略有不同,即电缆中的色散现象[18]。图6为某型号10kV电缆的实测波速,可以看出,电缆波速在较低频段区间变化较大,这种变化会导致反射系数实部中各周期分量发生相位偏移,为了直观说明这种现象,构建周期分量1为

式中,为图6所示实测电缆相速度。f=0.01~80MHz,f的间隔为0.01MHz。
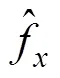

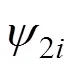


图7 y1和y2的对比结果

3.3 初始相位判断波形极性
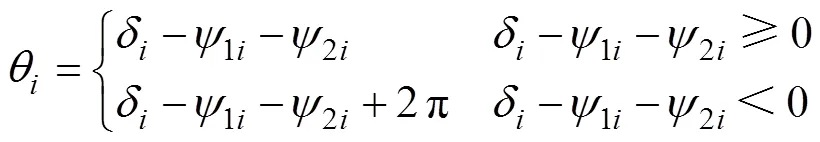
结合式(17)可以得到,当=0°时,该反射波形为正极性;当=180°时,该反射波形为负极性。在实际测试中,综合考虑测量误差和计算误差的影响,提出FDR的波形极性判断条件如图8所示。当处于一、四象限,实轴正半轴或虚轴正半轴时,判断该反射波为正极性;当处于二、三象限,实轴负半轴或虚轴负半轴时,判断该反射波为负极性。
4 仿真算例
为了验证本文所提方法判断FDR中反射波极性的准确性,本文分别对单反射波和多反射波两类情况进行验证。需要说明的是,本文仿真仅讨论传播距离小于电缆末端反射波的反射波。本文采用Matlab软件仿真10kV的交联聚乙烯电缆,具体的电缆参数[18-19]见表1。
表1 电缆模型参数
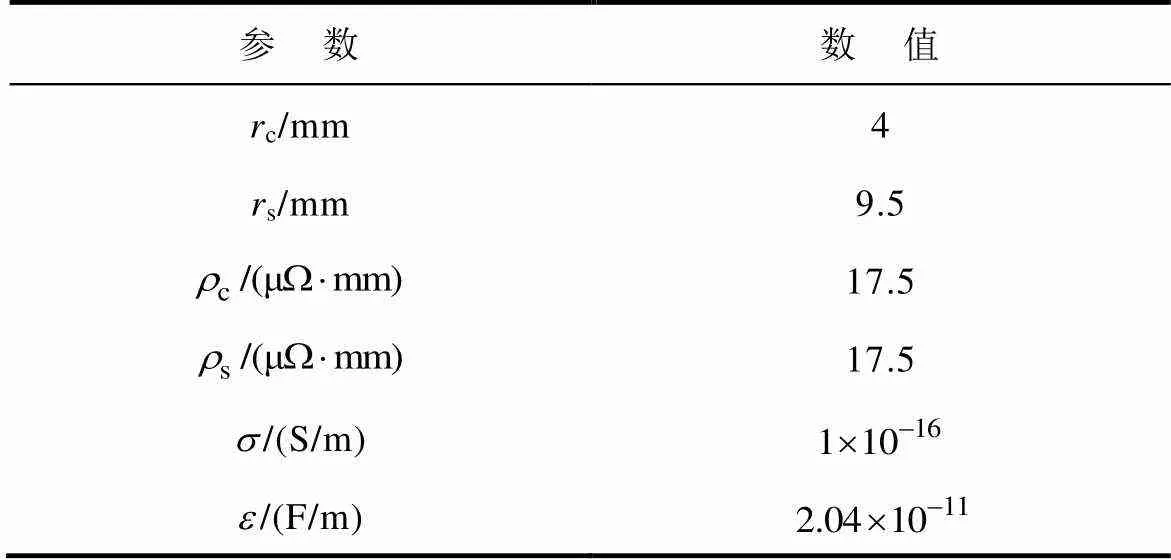
Tab.1 The parameters of cable model
4.1 单反射波
本文采用常见的过渡电阻接地故障模拟电缆中单反射波的情况,其模型如图9所示。图9中,g为过渡电阻,本文分别将其设置为20W、200W和2kW。FDR中频段选择为0.15~80MHz,s= 0.005MHz。利用本文算法识别FDR中反射波如图10所示,得到极性判断结果见表2。从图10可以看出,FDR的反射波识别可以确定电缆中反射波的传播距离,但是无法直接判断其极性。表2的数据证明了本文方法判断FDR中反射波极性的准确性。
对图9中电缆模型进行TDR测试分析,得到其反射波识别结果如图11所示。从图11可以看出,当g=20W时,接地故障位置阻抗变化程度较大,1反射波能量较强,TDR能够成功识别该反射波并判断其极性。当g增加时,接地故障位置阻抗变化程度变小,1反射波能量变弱,TDR中1的识别效果变差。当g=2kW时,TDR已经无法识别1,而FDR仍能够准确识别1。因此对于接地电阻过高的高阻接地而言,FDR可以准确地识别该反射波,证明了FDR相比于TDR能更好地识别电缆中微弱的反射波。

图9 单反射波的电缆模型

图10 单反射波的FDR识别结果
表2 单反射波的极性判断结果

Tab.2 The polarity judgment results of single reflected wave

图11 单反射波的TDR识别结果
4.2 多反射波
本文通过改变电缆中一段区域的特性阻抗来制作电缆中多反射波的情况,其模型如图12所示,图中,阻抗变化段的特性阻抗设置为原来的1.005倍。FDR中频段选择为0.15~80MHz,s=0.005MHz。利用本文算法识别该模型的FDR反射波如图13所示,得到反射波极性判断结果,见表3。图13同样说明了FDR的波形识别图虽然可以识别反射波1、2和3并判断其传播距离,但是无法判断其极性。表3表明即使存在多个反射波时,本文方法也可以有效判断FDR中反射波极性。
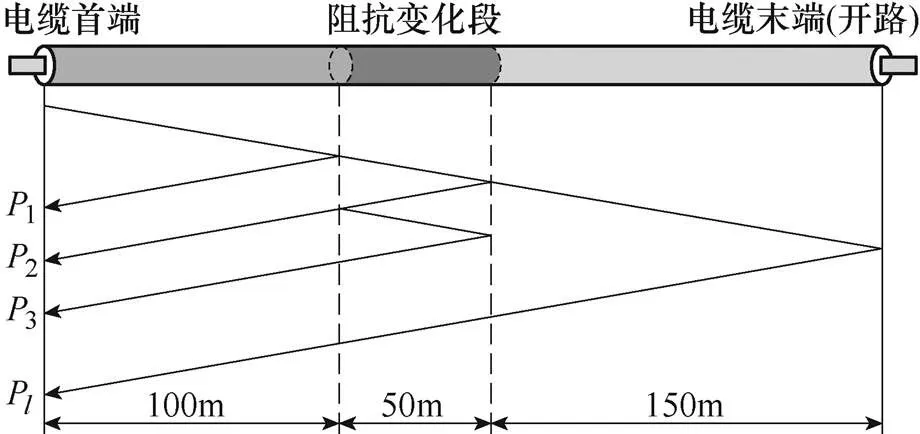
图12 多反射波的电缆模型
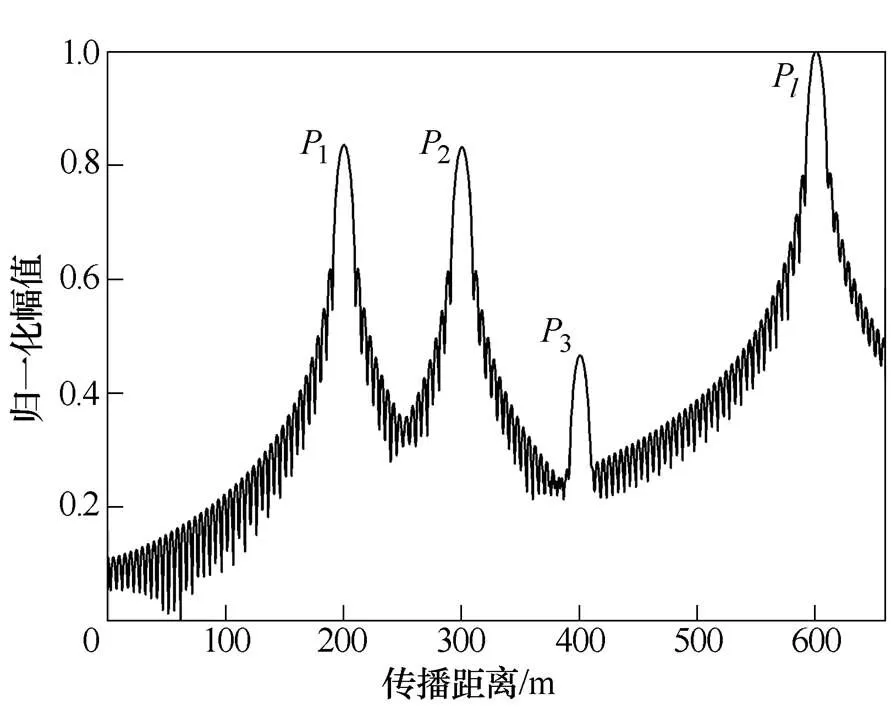
图13 多反射波的FDR识别结果
表3 多反射波的极性判断结果
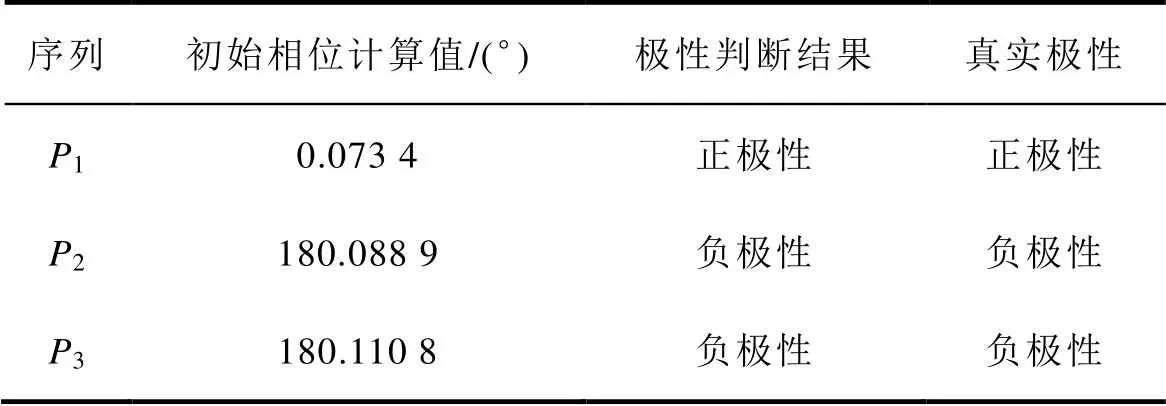
Tab.3 The polarity judgment results of multiple reflected waves
对图12中的电缆模型进行TDR测试,得到TDR测试结果如图14所示。对比图13和图14可以看出,对于反射能量较强的反射波1和2,TDR和FDR均能有效识别,并且都能准确地判断其波形极性;但是对于反射能量较弱的反射波3而言,FDR仍可以有效识别并准确地判断其波形极性,但是TDR无法进行识别,该仿真同样证明了FDR能够有效识别电缆中微弱的反射波。

图14 多反射波的TDR识别结果
5 实验验证
为了实际验证本文所提方法判断FDR中反射波极性的有效性,在实验室中将105m 10kV交联聚乙烯电力电缆在距首端43m处进行盐水腐蚀破坏。在进行一段时间的腐蚀破坏后,该位置的铜屏蔽层出现了铜绿,因此判断该电缆中出现了阻抗异变点,对该电缆进行FDR测试,如图15所示。

图15 FDR的测试系统示意图
图15中,在控制PC的控制下,调频信号发生器产生调频信号,该信号借助功分器实现信号能量的平分,平分后的一半信号成为入射信号经过耦合器之后传播到电缆中;平分后的另一半信号成为参考信号直接被数据采集模块捕获。当入射信号传播到电缆中后,会引发电缆的行波反射现象,进而产生反射信号,反射信号会由电缆向耦合器方向传播,在耦合器的作用下反射信号被捕获到数据采集装置中。此时数据采集装置同时采集得到参考信号和反射信号,计算得到反射系数谱并将其返回给控制PC,进而完成FDR中反射系数谱的测试。
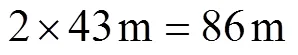

图16 实测的FDR识别结果

图17 实测的TDR识别结果
6 结论
本文针对传统FDR方法无法判断反射波极性,即无法判断阻抗异变点类型的问题,提出了一种新的FDR反射波极性判断方法,该方法首先对FDR中反射系数实部进行周期分量分析,利用其频率值和修正后的相位值分别计算反射波的传播距离和判断其极性。通过对仿真和实测分析,得到以下结论:
1)本文通过分析传输线理论,证明了利用FDR中反射系数实部进行反射波识别的可行性。
2)HSCW的FFT插值算法改善了原有FDR方法中参数难以确定和计算效率低的问题,同时其周期分量的谱间干扰抑制效果较好,利于FDR的反射波识别。
3)在利用相位判断反射波极性之前,需要对FDR测试下限频率和频变波速造成的相位偏差进行修正,以提高极性判断的准确率。
4)仿真和实际测试结果表明,本文所提方法可以有效计算FDR中反射波的传播距离和判断其极性,可以进一步定位电缆局部缺陷和故障等阻抗异变点并判断其类型。
[1] 周凯, 谢敏, 赵世林, 等. 基于改进FastICA的局部放电在线监测窄带干扰高保真性抑制方法[J]. 电工技术学报, 2018, 33(11): 2604-2612.
Zhou Kai, Xie Min, Zhao Shilin, et al. Periodic narrowband noise rejection with high fidelity of partial discharge on line monitoring based on improved FastICA algorithm[J]. Transactions of China Elec- trotechnical Society, 2018, 33(11): 2604-2612.
[2] 饶显杰, 周凯, 谢敏, 等. 稳定图法在极化等效电路参数辨识中的应用[J]. 电工技术学报, 2020, 35(10): 2248-2256.
Rao Xianjie, Zhou Kai, Xie Min, et al. Application of stabilization diagram method for solving polarization equivalent circuit parameters[J]. Transactions of China Electrotechnical Society, 2020, 35(10): 2248- 2256.
[3] 李长明, 伍国方, 李春阳, 等. XLPE绝缘高压直流电缆终端内缺陷对电场分布的影响[J]. 电机与控制学报, 2018, 22(12): 62-67.
Li Changming, Wu Guofang, Li Chunyang, et al. Effect of the defects inside XLPE insulated HVDC cable termination on the electric field distribution[J].
Electric Machines and Control, 2018, 22(12): 62-67.
[4] 乐彦杰, 汪洋, 郑新龙, 等. 交联聚乙烯与浸渍纸绝缘直流电缆接头电场分布[J]. 电机与控制学报, 2019, 23(2): 75-86.
Le Yanjie, Wang Yang, Zheng Xinlong, et al. Electric field distributions in the joint of XLPE and mass impregnated HVDC cables[J]. Electric Machines and Control, 2019, 23(2): 75-86.
[5] 李露露, 雍静, 曾礼强, 等. 基于系统电力扰动的交叉互联电缆绝缘整体老化在线监测[J]. 电工技术学报, 2018, 33(14): 3396-3405.
Li Lulu, Yong Jing, Zeng Liqiang, et al. On-line monitoring of insulation overall aging for cross- bonded cables based on system power disturbances[J]. Transactions of China Electrotechnical Society, 2018, 33(14): 3396-3405.
[6] 秦雪, 钱勇, 许永鹏, 等. 基于2D-LPEWT的特征提取方法在电缆局部放电分析中的应用[J]. 电工技术学报, 2019, 34(1): 170-178.
Qin Xue, Qian Yong, Xu Yongpeng, et al. Appli- cation of feature extraction method based on 2D- LPEWT in cable partial discharge analysis[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 170- 178.
[7] 李露. 船用电力电缆故障诊断的仿真研究[D]. 大连: 大连理工大学, 2017.
[8] 李保生. 基于时域脉冲反射原理的电线电缆精确测长技术研究[D]. 西安: 西安电子科技大学, 2010.
[9] 张俊民, 魏娟, 谢华博, 等. 基于时域反射法的航空导线绝缘故障检测与分析[J]. 航空学报, 2009, 30(4): 706-712.
Zhang Junmin, Wei Juan, Xie Huabo, et al. Detection and analysis of aerospace wire insulation faults based on TDR[J]. Acta Aeronouticaet Astronautica Sinica, 2009, 30(4): 706-712.
[10] 吴春华, 胡雅, 李智华, 等. 基于SSTDR的光伏系统直流母线电弧故障在线检测与定位[J]. 中国电机工程学报, 2020, 40(8): 2725-2735.
Wu Chunhua, Hu Ya, Li Zhihua, et al. On-line detection and location of DC bus arc faults in PV systems based on SSTDR[J]. Proceedings of the CSEE, 2020, 40(8): 2725-2735.
[11] Shi Qinghai, Kanoun O. Wire fault diagnosis in the frequency domain by impedance spectroscopy[J]. IEEE Transactions on Instrumentation and Measure- ment, 2015, 64(8): 2179-2187.
[12] Hirai N, Yamada T, Ohki Y. Comparison of broad- band impedance spectroscopy and time domain refle- ctometry for locating cable degradation[C]//IEEE International Conference Condition Monitoring and Diagnosis, Bali, Indonesia, 2012: 229-232.
[13] Zhou Zhiqiang, Zhang Dandan, He Junjia, et al. Local degradation diagnosis for cable insulation based on broadband impedance spectroscopy[J]. IEEE Transa- ctions on Dielectrics and Electrical Insulation, 2015, 22(4): 2097-2107.
[14] Ohki Y, Yamada T, Hirai N. Precise location of the excessive temperature points in polymer insulated cables[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2013, 20(6): 2099-2106.
[15] Ohki Y, Yamada T, Hirai N. Diagnosis of cable aging by broadband impedance spectroscopy[C]//IEEE Conference on Electrical Insulation and Dielectric Phenomena, Cancun, Mexico, 2011: 24-27.
[16] 谢敏, 周凯, 赵世林, 等. 新型基于反射系数谱的电力电缆局部缺陷定位方法[J]. 电网技术, 2017, 41(9): 3083-3089.
Xie Min, Zhou Kai, Zhao Shilin, et al. A new location method of local defects in power cables based on reflection coefficient spectrum[J]. Power System Technology, 2017, 41(9): 3083-3089.
[17] 周志强. 基于宽频阻抗谱的电缆局部缺陷诊断方法研究[D]. 武汉: 华中科技大学, 2015.
[18] 谢敏, 周凯, 赵世林, 等. 考虑相速度频变效应的改进互相关算法局部放电定位[J]. 电网技术, 2018, 42(5): 1661-1667.
Xie Min, Zhou Kai, Zhao Shilin, et al. Research on partial discharge location using modified cross- correlation method considering frequency characteri- stic of phase velocity[J]. Power System Technology, 2018, 42(5): 1661-1667.
[19] 谢敏, 周凯, 何珉, 等. 基于时间反演技术的电力电缆局部放电定位方法[J]. 中国电机工程学报, 2018, 38(11): 3402-3409.
Xie Min, Zhou Kai, He Min, et al. Partial discharge location for power cable based on the time reversal technique[J]. Proceedings of the CSEE, 2018, 38(11): 3402-3409.
[20] 洪博, 王莉, 毛健美, 等. 一种航天器一次母线故障在线检测定位方法[J]. 电工技术学报, 2016, 31(5): 118-125.
Hong Bo, Wang Li, Mao Jianmei, et al. An on-line detection and location method for primary bus fault of spacecraft[J]. Transactions of China Electro- technical Society, 2016, 31(5): 118-125.
[21] 王永, 滕召胜, 李建闽, 等. 基于采样序列重构的高精度介质损耗角测量方法[J]. 电工技术学报, 2018, 33(23): 5607-5615.
Wang Yong, Teng Zhaosheng, Li Jianmin, et al. High accuracy dielectric loss angle measurement method based on sampling sequence reconstruction[J]. Transactions of China Electrotechnical Society, 2018, 33(23): 5607-5615.
[22] 段虎明, 秦树人, 李宁. 离散频谱的校正方法综述[J]. 振动与冲击, 2007(11): 138-145, 189.
Duan Huming, Qin Shuren, Li Ning. Review of correction methods for discrete spectrum[J]. Journal of Vibration and Shock, 2007(11): 138-145, 189.
[23] 温和, 滕召胜, 卿柏元. Hanning自卷积窗及其在谐波分析中的应用[J]. 电工技术学报, 2009, 24(2): 164-169.
Wen He, Teng Zhaosheng, Qing Baiyuan. Hanning self-convolution windows and its application to harmonic analysis[J]. Transactions of China Electro- technical Society, 2009, 24(2): 164-169.
Type Judgement Technology of Impedance Variation in Frequency Domain Reflection Method
(School of Electrical Engineering Sichuan University Chengdu 610065 China)
The reflection of the traveling wave can be used to detect the impedance variation of cable including local defects and faults. The propagation distance and polarity of the reflected wave are respectively used to locate the impedance variation position and judge the type of the impedance variation. Frequency domain reflection (FDR) is one of the effective means to identify the reflected wave in the cable. However, the traditional FDR method can only obtain the propagation distance of the reflected wave, but cannot judge the polarity of the reflected wave. Therefore, this paper presents a polarity judgement technology for the reflected wave in FDR. Firstly, this paper describes the principle of reflected wave identification in FDR, and analyzes the reflection coefficient in FDR by the fast Fourier transform interpolation algorithm of Hanning self-convolution windows. The phase deviations caused by lower limit frequency of FDR and frequency-dependent wave velocity are corrected, and the frequency value and the modified phase value are respectively used to obtain the propagation distance and the polarity of the reflected wave. Then, the cable model of single reflected wave and multiple reflected wave is simulated. Finally, the proposed method is verified by experiments on a 105m 10kV cross-linked polyethylene cable. The results show that the method proposed can effectively obtain the propagation distance and polarity of the reflected wave in FDR.
Frequency domain reflectometry (FDR), reflected wave, polarity judgement, Hanning self-convolution windows, phase correction
10.19595/j.cnki.1000-6753.tces.200463
TM41
饶显杰 男,1996年生,硕士,研究方向为电力设备状态监测。E-mail: 1953520244@qq.com
周 凯 男,1975年生,教授,博士生导师,研究方向为电缆绝缘状态检测与修复等。E-mail: zhoukai_scu@163.com(通信作者)
国家自然科学基金资助项目(51477106)。
2020-05-06
2020-06-16
(编辑 崔文静)
