高功率密度SiC静止无功补偿器强迫风冷散热综合建模及优化设计方法

林弘毅 伍 梁 郭 潇 陈国柱

高功率密度SiC静止无功补偿器强迫风冷散热综合建模及优化设计方法

林弘毅 伍 梁 郭 潇 陈国柱

（浙江大学电气工程学院 杭州 310027）

为了提高大功率高功率密度电力电子装置热设计的准确性和设计效率，该文综合热传导、对流换热与流体力学理论，针对电力电子装置的典型强迫风冷散热系统，提出基于截面积二次方根为无量纲特征长度的综合热模型，并提出一种强迫风冷散热系统体积最优的优化设计方法。以380V/50kvar高功率密度静止无功补偿器（SVG）为例，比较所提出的综合热模型与温升实验的热阻，综合热模型平均热阻误差在7%以内，即在SVG满载运行时，散热器平均表面温升的绝对误差De在1.3℃以内。该文提出的综合热模型相对于传统热模型精度提升62%，证明了综合热模型的准确性。基于所提出的优化方法设计的散热系统体积4.03L，对比传统方法设计的体积5.7L，体积缩小30%，从而证明了该文提出优化设计方法的可行性。

热设计 热模型 强迫风冷 静止无功补偿器（SVG）

0 引言

电力电子器件在工作中会产生损耗，这些损耗会转化为热量。若热设计不合理，电力电子器件的结温过高，将导致电力电子器件的失效率增大，较高的过温还会造成器件烧毁，直接影响电力电子装置的寿命和可靠性。随着大功率电力电子装置向高功率密度发展，电力电子器件的散热问题越来越突出，进而影响了电力电子装置的可靠性和稳定性，成为电力电子装置功率密度进一步提高的瓶颈[1]。

随着宽禁带器件的发展，电力电子装置的开关频率得以提升，无源器件的体积显著减小[2-3]。对基于宽禁带器件的强迫风冷电力电子装置而言，散热系统（包括散热器和风扇）占装置总体积的25%以上。因此，散热系统体积优化对提高电力电子装置的功率密度起着关键作用。

目前，电力电子装置的热设计主要依赖工程实践经验。有些学者基于实践经验提出了一些经验公式，但经验公式通常误差较大，且不具有普遍适用性[4]。文献[5]采用HyperMesh和Fluent软件联合仿真进行散热设计，但是热设计过程缺乏理论支撑。文献[6]基于传统热模型，提出了散热系统的优化设计方法，对15V/2kA的高频、大功率开关电源样机进行散热设计，温度误差在3.8%以内。但是其在优化过程中仅利用热仿真软件对散热器几何尺寸进行优化，由于散热器变量较多且互相耦合，设计的效率较低。文献[7]基于传统热模型对20kW电动汽车SiC逆变器的散热器进行优化设计，热阻误差在15%以内，但是仅对散热器几何尺寸进行优化，忽略了风扇的影响。文献[8]基于传统热模型，对强迫风冷散热系统进行建模分析，并提出了一种衡量散热效果的新指标，但是其模型误差较大。

在电力电子装置设计之初，散热设计应该和电路设计、结构设计同步规划开展。散热系统设计流程如图1所示。值得注意的是，热设计包括理论计算、热仿真验证、模拟实验验证等流程，耗时较长。因此，在热设计完成之前，可以先利用传统经验公式对散热进行概要设计，初步验证设计方案的可行性，并指导结构设计和功率PCB布局。在热设计的过程中，电路测试可以同步进行，以提升设计效率。

本文首先介绍了380V/50kvar静止无功补偿器（Static Var Generator, SVG）系统的电路拓扑和主要参数，并分析了SVG系统的损耗，介绍了典型强迫风冷散热系统的结构及其热阻网络；然后利用传统经验公式对散热系统进行概要设计；接着综合热传导、对流换热与流体力学理论，针对电力电子装置的典型强迫风冷散热系统，提出了一种基于截面积二次方根为无量纲特征长度的综合热模型。同时，提出一种优化方法对风扇和散热器总体积进行优化；最后给出了散热系统有限元仿真和温升实验的结果。本文提出的综合热模型平均热阻误差在7%以内，经过折算，在SVG满载运行时，散热器平均表面温升的绝对误差De在1.3℃以内。而传统热模型[7-8]平均热阻误差为69%，证明了本文提出散热系统综合热模型的准确性。同时，对比了传统设计方法和本文提出优化设计方法的散热系统体积，基于优化方法设计的散热系统体积为4.03L，较传统经验公式设计的体积5.7L，缩小30%，证明了本文提出优化设计方法的可行性。

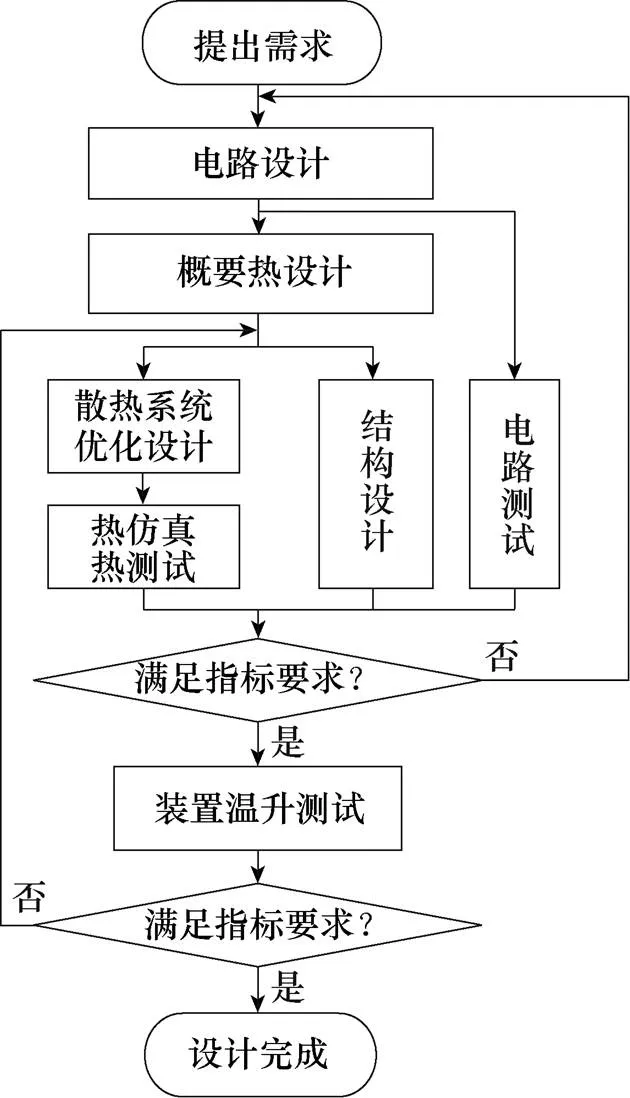
图1 系统设计流程

1 SiC-SVG损耗分析与散热器热阻网络

1.1 SiC-SVG电路设计与损耗分析

SVG系统的电路拓扑如图2所示。考虑成本，系统由两个模块并联而成，为了增加通流能力，每个开关由两个TO-247封装的SiC-MOSFET（型号SCT50N120）并联。系统的主要电路参数见表1。

图2 SVG电路拓扑

表1 SVG主要电路参数

Tab.1 Circuit parameters of SVG

图3 单个MOSFET损耗分布

1.2 典型强迫风冷散热系统结构及其热阻网络

典型强迫风冷散热系统结构示意图如图4所示，典型强迫风冷散热系统结构由轴流风扇、系统风道和翅片型散热器组成。

图4 典型强迫风冷散热系统结构示意图

翅片型散热器的宽为，长为，基板厚为，散热器基板的面积为hs，散热系统风道长度为duct。散热器有个风道，共+1个翅片，每个翅片的长为、厚为，相邻翅片间表面间距即散热器风道宽为。散热系统需要个风扇，其中，风扇厚为fan，高为fan。考虑风扇后，散热系统的总体积可定义

散热系统热阻模型如图5所示，Tj为MOSFET的结温，Tc为MOSFET的壳温，Th为散热器的表面温度，Ta为环境温度，Rth,j-c为MOSFET结壳之间的热阻，Rth,TIM为MOSFET与散热器之间热界面材料（Thermal Interface Material, TIM）的热阻，Rth,h-a为散热器与空气之间的热阻[11]。

TIM的热阻th,TIM与材料的热导率、材料硬度、表面光洁度、安装压力等因素相关，很难精确计算。由于固体之间接触并非理想接触，接触面之间存在微小的空气空隙。因此，需要在固体导热垫片两面均匀涂上导热硅脂，填充空气间隙，如图5所示，以提高TIM与散热器的接触面积，提高散热效率。TO-247封装TIM的热阻值见表2。

表2 常用TIM及其热阻

Tab.2 Common TIM and its thermal resistance

装置的拓扑如图2所示，其对应的等效热阻网络如图6所示。热阻为在物体两端温度差与热源的功率之间的比值。基于等效热阻网络和热阻定义可得

根据热阻定义与式（2）可推导得到电力电子装置允许的最大热阻th,h-a,max为

本文中设定器件的最大结温j,max=120℃，环境温度a,max=40℃。th,j-c=0.55℃/W，陶瓷垫片热阻th,TIM≈0.6℃/W。考虑散热器表面温度不均，温差为10℃，可求出满足电力电子装置允许的最大热阻th,h-a,max=0.030 6℃/W，即允许SVG满载时，散热器最大温升D=26.4℃，允许MOSFET壳最大温升Dc=48℃。

2 强迫风冷散热系统概要设计

本节利用传统经验设计方法对强迫风冷散热系统进行概要设计，经验设计方法的公式简单，但是准确性较差，容易导致裕度过大。概要设计的目的有：①论证项目的合理性，如装置体积、功率密度是否可以基本达到指标要求；②热设计过程较为繁琐，需要理论设计、热仿真、模拟实验等步骤，在完成完整的热设计之前，概要设计结果可以指导装置结构设计和PCB布局，提高设计效率。

2.1 风机概要选型

根据能量守恒原则，系统稳定时产生的热量与其散发的热量是相同的，由此可以得到流量0、系统产生的热量与空气温升Dair的关系为

式中，0为实际通过散热器风道空气的流量，即散热系统工作点；air为空气的密度，air1.23kg/m3；air为空气的比热容，air=1 005J/(kg·℃)；Dair为散热器出风口处的流体相对入风口的温度差。一般认为Dair＜5℃。

由于风道并非理想封闭，散热器对流体存在阻力，风机提供的最大流量将会大于实际通过散热器风道空气流量0。经验上认为风机提供的最大流量fan,max≈(1.5～2)0。

根据式（4）可知，本文SVG装置散热系统最小流量min=0.139m3/s。本文初选风扇型号为AGB08038_ 24H，数量5个，高度fan=80mm。可提供最大风量为5×0.04m3/s =0.2m3/s，风扇详细参数见表3。

表3 备选风扇型号参数

Tab.3 The fan list and parameters

2.2 散热器概要设计

散热器的散热面积hs须略大于功率半导体器件的总散热面积。翅片厚和散热器风道宽可根据经验在2～5mm之间选择。基板厚对系统总热阻影响不大，可以在满足安装的情况下取一个较小的值。为了结构设计方便和提高散热系统体积利用率，可令fan≤，fan+。风道长度为duct可取30～50mm。散热器的热阻主要取决于散热器风道流体换热的热阻th,A估算，即

式中，h为流体传热系数，在强迫风冷的条件下可取60～80。功率PCB上的功率器件分布示意图如图7所示。散热面积长80mm，宽为350mm。因此，本文取散热器宽b=400mm，翅片长c=60mm，基板厚度d=20mm，翅片厚和散热器风道宽可令其分别为t =3mm、s=2mm，可得翅片数为n=b/(s+t)=80。风道长度可取Lduct=40mm。令Rth,A=0.030 6℃/W，取h=70，根据式（5）估算得到散热器的长L≈100mm。根据式（1）可知，概要设计散热系统总体积为5.70L。基于经验公式概要设计的散热系统参数见表4。

表4 概要设计与优化设计散热器参数

Tab.4 The cooling system parameters

3 强迫风冷散热系统建模及优化设计

强迫风冷散热系统建模中，关键要得到表面传热系数。表面传热系数是一个过程量，与流体状态、流速、表面摩擦因数等物理量紧密相关。工程热物理学中，很难直接从理论推导出其表达式，通常会采用实验的方法总结归纳得出表达式，这种表达式又称之为实验关联式。

传统的实验关联式通常以水力直径作为无量纲特征长度，其适用的范围较广，但所造成的误差/不确定度较大，常常达到±25%[7-8]。文献[7-8]提出基于传统充分发展层流和湍流的实验关联式建立的传统热模型，所得到的平均热阻误差为69%。对电力电子装置的强迫风冷散热器而言，传统热模型误差偏大，准确性较低。

Yovanovich的物理实验结果表明，典型强迫风冷散热器风道窄而短，流体常常不能够充分发展，因此流体的状态通常为入口段层流[12-14]。由此，Yovanovich提出了适用于入口段层流的基于截面积二次方根为无量纲特征长度的实验关联式，误差/不确定度减小至±10%[13-14]。针对传统热模型误差偏大的情况，本文基于截面积二次方根为无量纲特征长度的实验关联式，综合热传导、对流换热与流体力学等理论进行建模，得到散热器热阻的平均热阻误差为7%。因此，本文提出的热模型更为准确，更适用于描述电力电子强迫风冷散热器。

3.1 散热器热阻模型

热设计最为关键的就是求出散热器配合风扇的热阻th,h-a。散热器单个风道热阻模型如图8所示。散热器热阻th,h-a由基板热传导热阻th,d、流体传热热阻th,conv和流体略过散热器风道引起流体温度变化的热阻th,fluid组成，即

基板热传导热阻th,d为

式中，hs为铝材料散热器的热导率，hs=210W/(m∙℃)。根据风道热阻模型可以列出散热器风道的流体传热热阻th,conv表达式为

式中，th,FIN为散热器翅片传导热阻；th,a、th,A分别为散热器风道与流体换流的热阻。文献[15]提出了一种简化热阻模型，同时考虑了流体传热热阻th,conv、流量热阻th,fluid表面传热的有效面积eff、散热器效率以及表面传热系数，分别表示为

在假设散热器表面温度均匀的情况下[13]，可以得出各项系数的值为

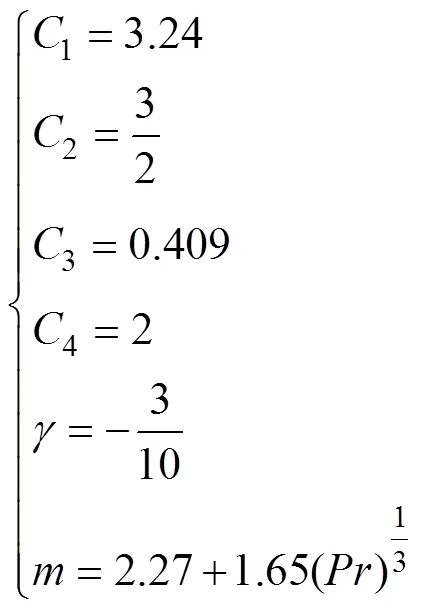
式中，air为空气的运动黏度，air=2.1×10-5m2/s。传热学中通常将摩擦因子与的相乘作为一项实验关联式[14]表示为

3.2 散热器与风扇流体力学模型

散热系统工作点0通过风扇的静压降特征式Dfan,k()和静压阻抗特征式Dtot()方程联立求解得

风扇并联的特点为：在相同的压强下，并联风扇的流量是单个风扇流量的倍。据此，可以得到多个风扇并联系统的静压降特征曲线。利用多阶多项式拟合该曲线，得到多个风扇并联系统的静压降特征式Dfan,k()为

式中，a（=0, 1, 2, 3, …）为拟合多项式的系数。为了得到散热系统工作点0，还需建立散热器的流体力学的模型，以求出散热器的静压阻抗特征式Dtot()。Dtot()主要由两部分构成：翅片散热器的静压阻抗Dhs()和系统风道的静压阻抗Dduct()[14]，分别表示为

翅片散热器的静压阻抗Dhs()、散热器出口处的截面积突增系数se、截面积散热器入口处的截面积突减系数sc、空气与散热器风道表面的摩擦因数app()以及系统风道的等效水力半径h,duct分别表

示[9, 14]为

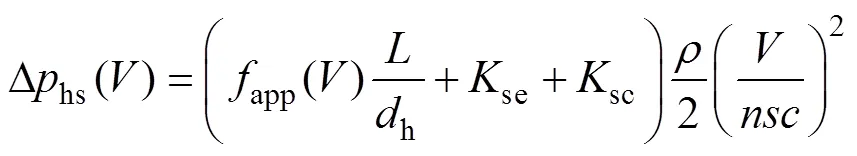
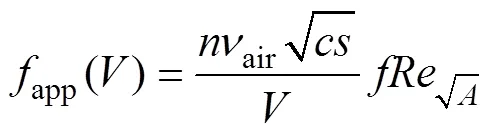
系统风道的静压阻抗Dduct()、空气与系统风道表面的摩擦因数app,duct()分别表示[9, 14]为

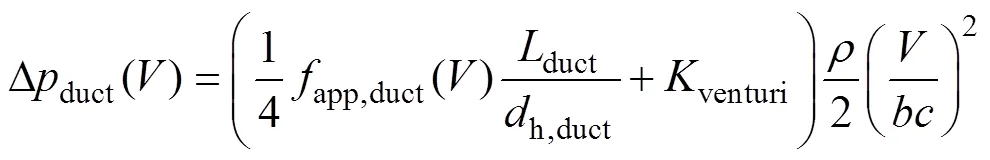
式中，venturi为效应摩擦因数，venturi≈0.2。根据式（6）～式（18）可知散热器热阻th,h-a()，根据式（19）～式（29）可求出散热系统的工作点0，散热器工作点热阻的求解过程如图9所示。根据 图9，可知概要设计的散热系统热阻th,h-a= 0.020 5℃/W。采用文献[7-8]所提出的传统热模型，计算得到热阻th,h-a=0.036 6℃/W，如图9所示。

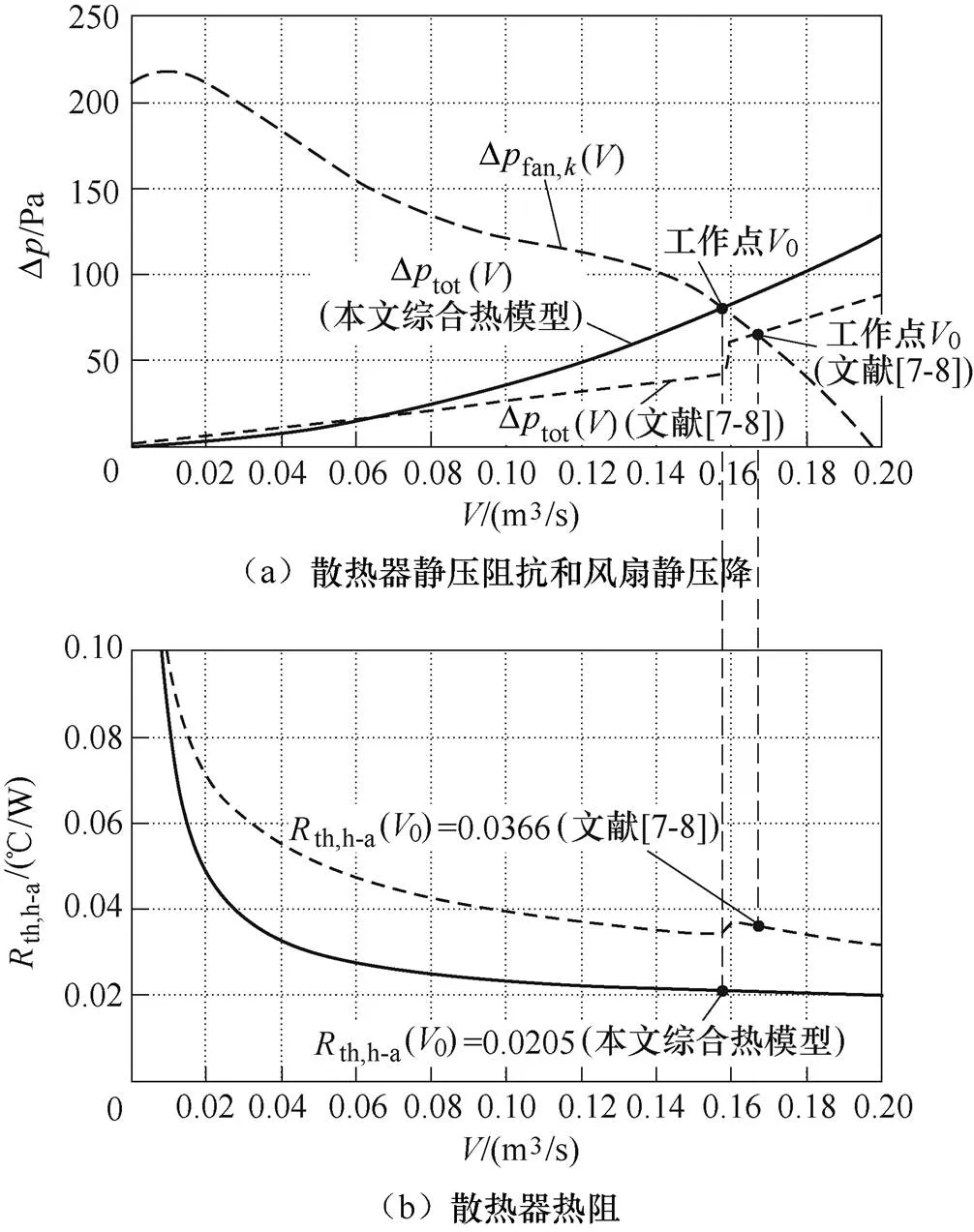
图9 散热器工作点热阻的求解过程

3.3 基于综合热模型的优化设计方法

散热器优化设计流程如图10所示。

（1）计算SVG满载情况下系统损耗，计算满足系统要求的最大热阻th,h-a,max。然后，根据整机结构要求、发热器件的分布、PCB布局，确定散热器结构参数取值范围。本文中，基板厚度应尽可能设置为更小的值，本文取20mm。根据图7中发热器件的分布，取散热器宽400mm≤≤450mm，长90mm≤≤120mm。散热器翅片风道宽，翅片厚度的取值范围取决于散热器厂家的工艺，本文取2mm≤≤20mm，2mm≤≤20mm。

（2）对备选的风扇进行扫描，本文中备选风扇型号见表3。为了提高系统空间的利用率，令散热器高等于风扇的高度fan，风扇的个数/fan向下取整。接着，根据式（20）拟合得到风扇的静压降特征曲线Dfan,k()。

（3）对散热器长、宽、风道宽、翅片厚度参数进行扫描，翅片参数的上、下限可分别表 示为

图10 散热器优化设计流程

（4）根据式（19）～式（29）得到散热系统的工作点0。.

（5）根据式（6）～式（18）求出散热器配合风扇的热阻th,h-a。

（6）当热阻th,h-a小于系统要求的最大热阻th,h-a,max时，输出散热系统参数、风扇型号以及散热系统的总体积h。

（7）输出该风扇型号对应的符合要求的散热器的体积h，以及该体积h下的最小热阻th,h-a（即翅片厚，风道宽最优）。对所有参数和风扇型号扫描后，选择最优的散热器-风扇组合。

图11为风扇FAN1～FAN6对应的散热系统体积h与最小热阻th,h-a曲线，从图11可知，th,h-a＜th,h-a,max的点均满足散热系统设计要求，其中优化后的散热器为A，其对应的参数见表4。与概要设计的散热器B相比，A的体积缩小了30%。

图11 散热系统体积Vh与最小热阻Rth,h-a曲线

4 散热系统仿真与实验分析

4.1 散热系统仿真验证

为验证本文提出优化设计方法的实用性与本文提出综合热模型的准确性，使用热仿真软件Flothem建立散热系统仿真模型，利用仿真软件中的热源模拟每个SiC-MOSFET的损耗。设置环境温度为25℃，发热功率为864W，TIM热阻为0.6℃/W。图12为散热系统仿真温度场稳态分布。概要设计和优化设计的散热系统热仿真结果见表5。表中，本文模型中假设散热器表面温度均匀，实际中散热器表面温度并不均匀，为验证模型的准确性，记录仿真中散热器表面温度的最大值和最小值，并用式（2）计算散热器的最大热阻和最小热阻。定义散热器热阻平均误差为

式中，th,sim,max为仿真中得到的散热器最大热阻；th,sim,min为仿真中得到的散热器最小热阻。但是由于散热器表面温度分布不均，高温度附近的功率器件将会承受更高的热应力，因此将散热器最大热阻误差定义为

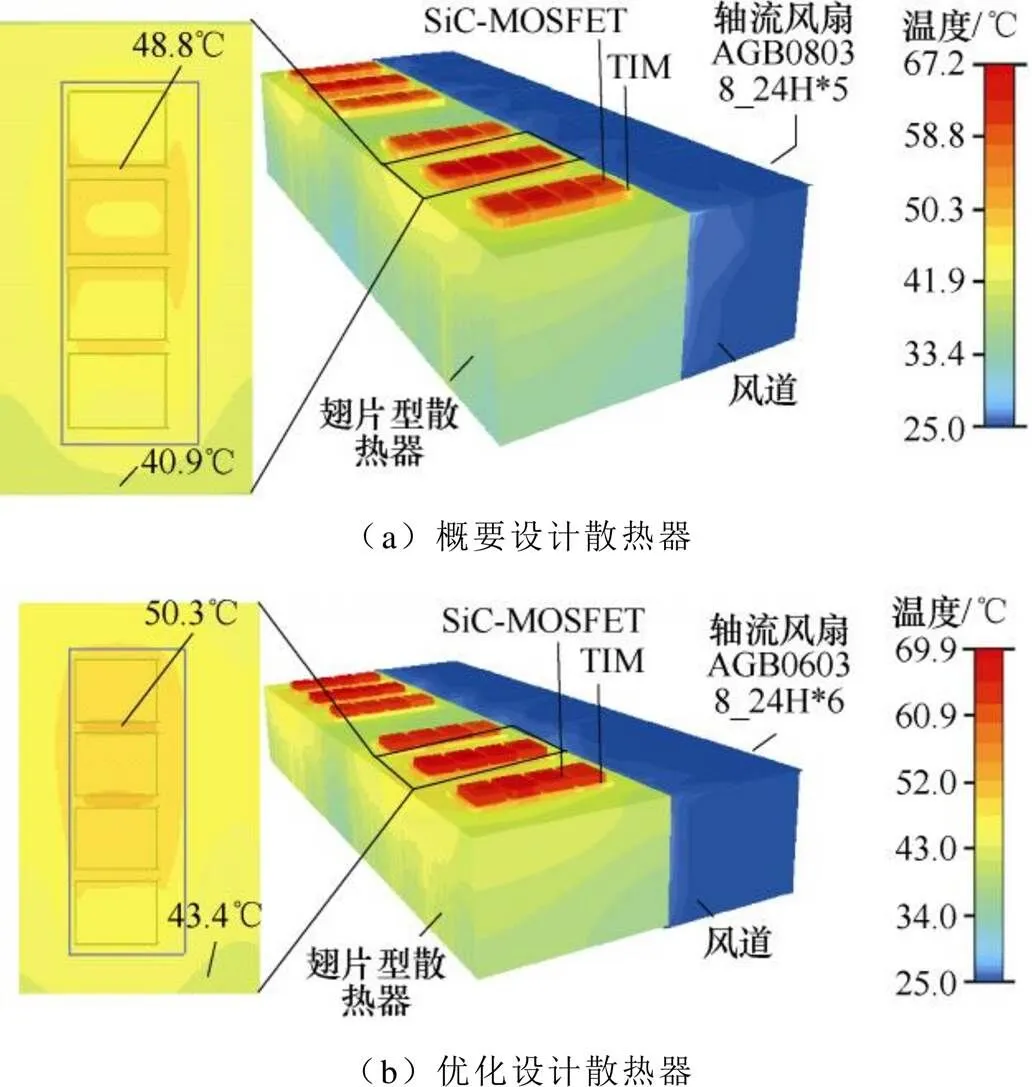
图12 散热系统仿真温度场稳态分布（Ta=25℃）

表5 散热系统仿真结果

Tab.5 Simulation results of cooling system

由图12仿真结果可以看出，两个散热系统的MOSFET壳最大温升均小于48℃，满足设计要求。本文提出综合热模型的理论计算热阻在仿真热阻值的区间内，平均热阻误差ave=6.6%，即SVG满载运行时，散热器平均表面温升的绝对误差De在1.2℃以内。最大热阻误差max=25%，即SVG满载运行时，散热器最大表面温升的绝对误差为De为5.6℃。仿真结果证明了本文提出的综合热模型的准 确性。

文献[7-8]的传统热模型得到的散热器热阻均高于仿真热阻的最大值，平均热阻误差ave=67%，即SVG满载运行时，散热器平均表面温升的绝对误差De高达13.7℃。最大热阻误差max=35%，即SVG满载运行时，散热器最大表面温升的绝对误差De为8.8℃。模型准确度较低。

4.2 散热系统实验测试

为验证本文提出优化设计方法的实用性与综合热模型的准确性，搭建380V/50kvar SVG测试平台，如图13所示。采用热电偶和温度巡检仪检测散热器表面位置的温度，温度稳定后，取散热器表面温度的最大值和最小值计算散热器的热阻，并记录温度最高MOSFET的壳温。

图13 散热系统测试平台

令SVG运行在开环有源逆变模式，向电网注入10～60kvar（即单相无功电流15～90A）的无功能量，通过功率分析仪（YOKOGAWA WT2030）测量SVG的输出无功功率和效率，即可计算出功率器件的总损耗。

不同功率下本文提出的综合热模型、文献[7-8]传统热模型、有限元仿真、温升实验测试的结果，如图14～图17所示。同时将本文提出的综合热模型和文献[7-8]传统热模型的理论温升D，一并绘在图14、图16中。在不同发热功率下，两个散热系统的MOSFET壳最大温升均小于Dc,max=48℃，满足设计要求。由于散热器表面温度不均，高温度附近的功率器件将会承受更高的热应力，因此，设计时需为此预留裕度。

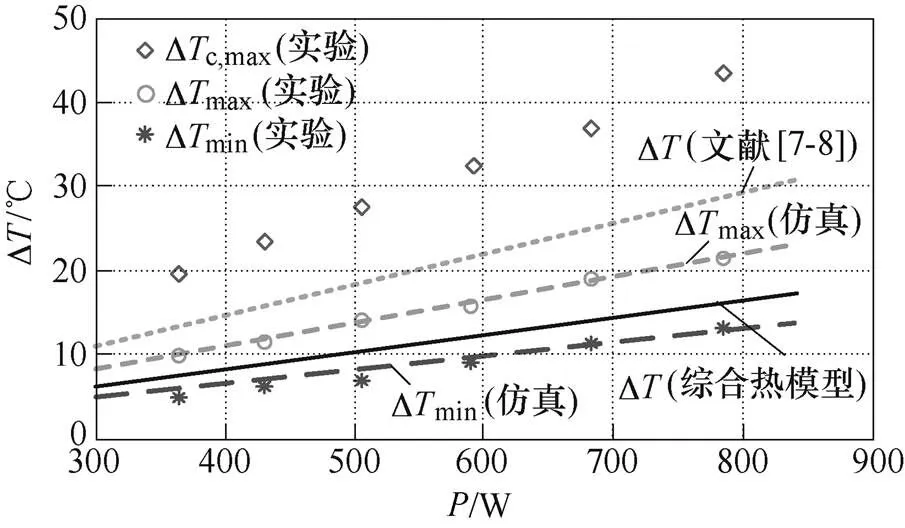
图14 概要设计散热器理论计算、热仿真和实验温升

图15 概要设计散热器理论计算、热仿真和实验热阻

图16 优化设计散热器理论计算、热仿真和实验温升

图17 优化设计散热器理论计算、热仿真和实验热阻

图15、图17中，本文提出的综合热模型理论计算热阻在实验测试热阻值的区间内，平均热阻误差ave在7.0%以内，即SVG满载运行时，散热器平均表面温升的绝对误差De在1.3℃以内，较传统散热模型提高62%。最大热阻误差max=26%，即SVG满载运行时，散热器最大表面温升的绝对误差De在5.8℃以内。

文献[7-8]的传统热模型得到的散热器热阻均高于实验测试热阻的最大值，平均热阻误差ave=69%，即SVG满载运行时，散热器平均表面温升的绝对误差De高达14℃，最大热阻误差为max=32%，即SVG满载运行时，散热器最大表面温升的绝对误差De为8.2℃。

实验结果验证了本文提出综合热模型的准确性，证明了该模型更适用于电力电子装置强迫风冷散热设计。

5 结论

电力电子装置热设计对高功率密度大功率电力电子装置的可靠性起着重要作用。为了提高热设计的准确性和设计效率，本文综合传热学与流体力学理论，提出了一种基于截面积二次方根为无量纲特征长度的综合热模型。同时，提出了一种针对典型强迫风冷散热系统的体积最优的优化方法，该优化方法亦可推广到质量最优、损耗最优等优化设计当中。以380V/50kvar高功率密度SVG为例，利用本文提出的方法设计的散热系统，较传统概要方法体积可缩小30%。对所设计的散热系统进行热仿真和温升测试，本文提出的综合热模型、热仿真、实验测试平均热阻误差ave在7%以内，即SVG满载运行时，散热器平均表面温升的绝对误差De=1.3℃。相较于传统热模型[7-8]平均热阻误差ave=69%，本文提出的综合热模型准确性有较大的提升。

[1] Laloya E, Lucía Ó, Sarnago H, et al. Heat manage- ment in power converters: from state of the art to future ultrahigh efficiency systems[J]. IEEE Transa- ctions on Power Electronics, 2016, 31(11): 7896- 7908.

[2] 周林, 李寒江, 解宝, 等. SiC MOSFET的Saber建模及其在光伏并网逆变器中的应用和分析[J]. 电工技术学报, 2019, 34(20): 4251-4263.

Zhou Lin, Li Hanjiang, Xie Bao, et al. Saber modeling of SiC MOSFET and its application and analysis in photovoltaic grid-connected inverter[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4251-4263.

[3] 肖龙, 伍梁, 李新, 等. 高频LLC变换器平面磁集成矩阵变压器的优化设计[J]. 电工技术学报, 2020, 35(4): 758-766.

Xiao Long, Wu Liang, Li Xin, et al. Optimal design of planar magnetic integrated matrix transformer for high frequency LLC converter[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 758-766.

[4] 胡建辉, 李锦庚, 邹继斌, 等. 变频器中的IGBT模块损耗计算及散热系统设计[J]. 电工技术学报, 2009, 24(3): 159-163.

Hu Jianhui, Li Jingeng, Zou Jibin, et al. Losses calculation of IGBT module and heat dissipation system design of inverters[J]. Transactions of China Electrotechnical Society, 2009, 24(3): 159-163.

[5] 丁杰, 张平. 电机控制器用IGBT风冷散热器的热仿真与实验[J]. 电源学报, 2015, 13(2): 38-44.

Ding Jie, Zhang Ping. Thermal analysis and experi- mental of IGBT air-cooled radiator for motor controller[J]. Journal of Power Supply, 2015, 13(2): 38-44.

[6] 何文志, 丘东元, 肖文勋, 等. 高频大功率开关电源结构的热设计[J]. 电工技术学报, 2013, 28(2): 185-191, 218.

He Wenzhi, Qiu Dongyuan, Xiao Wenxun, et al. Thermal design of high frequency high power switched- mode power supply[J]. Transactions of China Electro- technical Society, 2013, 28(2): 185-191, 218.

[7] 刘超, 贾晓宇, 胡长生, 等. 电动汽车SiC MOSFET风冷逆变器的散热器设计[J]. 电源学报, 2018, 16(3): 151-157.

Liu Chao, Jia Xiaoyu, Hu Changsheng, et al. Design of heat sink for electric vehicle SiC MOSFET air- cooled inverter[J]. Journal of Power Supply, 2018, 16(3): 151-157.

[8] Drofenik U, Stupar A, Kolar J W. Analysis of theoretical limits offorced-air cooling using advanced composite materials with high thermal conducti- vities[J]. IEEE Transactions on Components, Pack- aging and Manufacturing Technology, 2011, 4(11): 528-535.

[9] Kolar J W, Zach F C, Casanellas F. Losses in PWM inverters using IGBTs[J]. IEE Proceedings-Electric Power Applications, 1995, 142(4): 285-288.

[10] 白保东, 陈德志, 王鑫博. 逆变器IGBT损耗计算及冷却装置设计[J]. 电工技术学报, 2013, 28(8): 97- 106.

Bai Baodong, Chen Dezhi, Wang Xinbo. Loss calculation of inverter IGBT and design of cooling device[J]. Transactions of China Electrotechnical Society, 2013, 28(8): 97-106.

[11] 传热学. 电力电子器件热管理[M]. 北京: 机械工业出版社, 2013.

[12] Gammeter C, Krismer F, Kolar J W. Weight optimi- zation of a cooling system composed of fan and extruded-fin heat sink[J]. IEEE Transactions on Industry Applications, 2015, 51(1): 2193-2200.

[13] Muzychka Y S, Yovanovich M M. Laminar forced convection heat transfer in the combined entry region of non-circular ducts[J]. Journal of Heat Transfer, 2004, 126(1): 54-61.

[14] Muzychka Y S, Yovanovich M M. Pressure drop in laminar developing flow in noncircular ducts: a scaling and modeling approach[J]. Journal of Fluids Engineering, 2009, 131(11): 105-111.

[15] Simons R E. A simple thermal resistance model isoflux versus isothermal[J]. Electronics Cooling, 2006, 13(6): 10-14.

A Comprehensive Model of Forced Air Cooling and Optimal Design Method of High Power Density SiC-Static Var Generator

（College of Electrical Engineering Zhejiang University Hangzhou 310027 China）

Base on a novel characteristic length scale (the square root of cross-sectional), a comprehensive thermal model for the typical forced air cooling system of power electronic devices was proposed integrating heat conduction, convection heat transfer and fluid mechanics theories. In order to improve the accuracy and efficiency of the thermal design, an optimized design method for the optimal volume was proposed for the high-power and high-density power electronic device. Taking a 380V/50kvar high power density static var generator (SVG) as an example, compared with the experimental results, the average thermal resistance error of the comprehensive thermal model is within 7%, that is, the corresponding surface temperature rise is within 1.3℃ when SVG is running at full load. The accuracy of the comprehensive thermal model is improved by 62% compared with the traditional thermal models. Consenquently, the demention volume of the cooling part designed based on the proposed method is 4.03L, which is 30% smaller than the volume of 5.7L designed by the traditional methods.

Thermal design, thermal model, forced air cooling, static var generator (SVG)

10.19595/j.cnki.1000-6753.tces.200821

TM762; O551

林弘毅 男，1996年生，博士研究生，主要研究方向为电能质量、宽禁带器件应用。E-mail: lhy2007.11@qq.com

陈国柱 男，1967年生，教授，博士生导师，主要研究方向为大功率电力电子装置及其数字控制、有源电能质量控制技术及可再生能源发电并网技术。E-mail: gzchen@zju.edu.cn（通信作者）

国家自然科学基金资助项目（51777186）。

2020-07-09

2020-09-12

（编辑 陈 诚）