基于V型三段磁极错位削弱永磁直线电机推力波动的方法

兰志勇 谢 斌 祝涤非 金维宇

基于V型三段磁极错位削弱永磁直线电机推力波动的方法

兰志勇1谢 斌1祝涤非2金维宇3

（1. 湘潭大学信息工程学院 湘潭 411105 2. 上海策永自动化科技有限公司 上海 200120 3. 威胜电气有限公司 湘潭 411105）

6槽7极单边平板型永磁同步直线电机（PMLSM）运行过程中会产生推力波动，导致机床加工精度变差。针对此问题，提出一种将磁极错位与V型磁极相结合的优化方法来改善其性能。首先采用许克变换法对端部磁场进行分析，得到由端部效应引起的总推力波动解析表达式，再对解析式中傅里叶系数进行分析，得出端部效应引起推力波动的主要谐波次数；然后通过对多种永磁体结构进行有限元仿真，由力特性得出采用V型三段错位磁极的方法，当两端磁极与中间磁极所产生的谐波相位互差90°时可有效削弱推力波动；最后根据此方法制作样机。有限元结果及样机实验验证了此方法的可行性，对单边平板型PMLSM优化设计有着重要的指导意义。

V型三段磁极错位 许克变换法 磁阻力 端部推力波动 永磁同步直线电机 有限元仿真

0 引言

单边有铁心永磁同步直线电机（Permanent Magnet Linear Synchronous Motor, PMLSM）由于推力大、精度高、结构简单等优点，在直驱领域的应用日趋广泛。PMLSM可看作是由永磁同步电机沿径向切开并拉直演变而来，因此直线电机无法像旋转电机一样首尾相连，这也导致切开处气隙磁场产生畸变进而电机推力产生波动，采用开口槽也会导致推力波动的产生，即端部力与齿槽力[1-4]。

目前，国内外对电机推力波动的削弱主要从电机本体、控制策略等方面进行研究。采用不同极槽配合与斜极的方法来削弱磁阻力，该方法能有效减小电机推力波动[5-7]。文献[8-11]采用数值计算的方法对永磁同步伺服直线电机磁阻力进行研究，提出可通过改变端部齿结构与磁极形状使推力波动最小，同时齿槽磁阻力也得以削弱。文献[12]首先推导出最小端部力与初级长度的关系式，然后通过改变初级长度来研究端部磁阻力，并在最优初级长度的基础上运用分磁环理论抑制端部磁阻力。文献[13]采用辅助极一体式结构来削弱端部磁阻力，初级铁心与增加的辅助极用隔磁磁桥相连，可有效消除误差来源，同时电机的机械强度也得到提升。文献[14]提出可通过把初级端面做成V型来减小电机磁阻力，对V型端部进行阶梯化处理能有效削弱端部磁阻力。文献[15]提出一种双动子双侧Halbach永磁阵列直线电机，通过优化电机磁极结构提升电机磁能密度来降低电机磁阻力。文献[16]提出一种交替极结构中增加两块切向充磁永磁体，构成Halbach交替极结构，可削减极间漏磁并增大气隙磁通密度，并得出此结构有助于减小电机磁阻力。文献[17]提出将初级叠片分为上下两部分，且相数由三相增加到六相，并在此基础上对永磁体进行倒角来减小齿槽力。文献[18]采用V型线圈并通过等效磁化强度法进行模型解析，利用遗传算法对电机设计进行局部优化，最后得到局部推力波动最小的电机模型。文献[19]将初级铁心与次级磁极都采用V型结构，此结构能有效削弱端部效应和齿槽效应，电机推力波动也大为减小，但是推力却大幅降低，且初级V

型端部会产生尖端饱和。文献[20-21]分析了永磁直线同步电机在运行过程中所产生的谐波，运用相位补偿角度减小电机推力波动。虽然以上文献都对电机推力波动进行了有效削弱，但同时推力幅值也明显降低。

本文以6槽7极单边有铁心永磁同步直线电机为研究对象，提出一种将磁极错位与V型磁极相结合的优化方法。首先基于许克变换法推导出不同永磁体结构下端部效应引起的推力波动解析表达式，通过对解析式中傅里叶系数进行分析，得出端部效应引起推力波动的主要谐波次数；然后对不同永磁体的结构进行有限元仿真，并对其仿真结果进行比较分析，发现V型三段磁极错位两端磁极与中间磁极所产生的谐波相位互差90°时，推力波动最小；为进一步验证此方法的正确性，使用实验平台对6槽7极永磁直线同步电机样机进行实验，并将测试结果与有限元仿真进行比较；最后，通过实验测试与有限元仿真结果对比验证了该方法的有效性。

1 基于许克变换法的端部力解析分析

1.1 端部磁通函数

端部磁通物理模型如图1所示，假设电机铁心磁导率为无穷大，1为磁极q轴与动子纵向端面的距离，穿过动子铁心纵向端部边缘的最大磁通为m1，并且磁通遵循磁路最短原则（磁极形成的磁场可看成一个个椭圆），在电机动子运行过程中穿过初级电枢铁心端面磁通发生周期性变化，当动子纵向端部运行到两磁极之间时穿过的磁通最大，随着动子继续运动，穿过端面的磁通会慢慢减少，动子运行到1=/2时，穿过初级电枢铁心端面磁通为0，电机继续运动时穿过端面的磁通又开始增加。当电机继续运动时，穿过电机初级铁心端面的磁通呈现一个周期性变化[2]。

穿过动子纵向端面磁通与1的关系式为

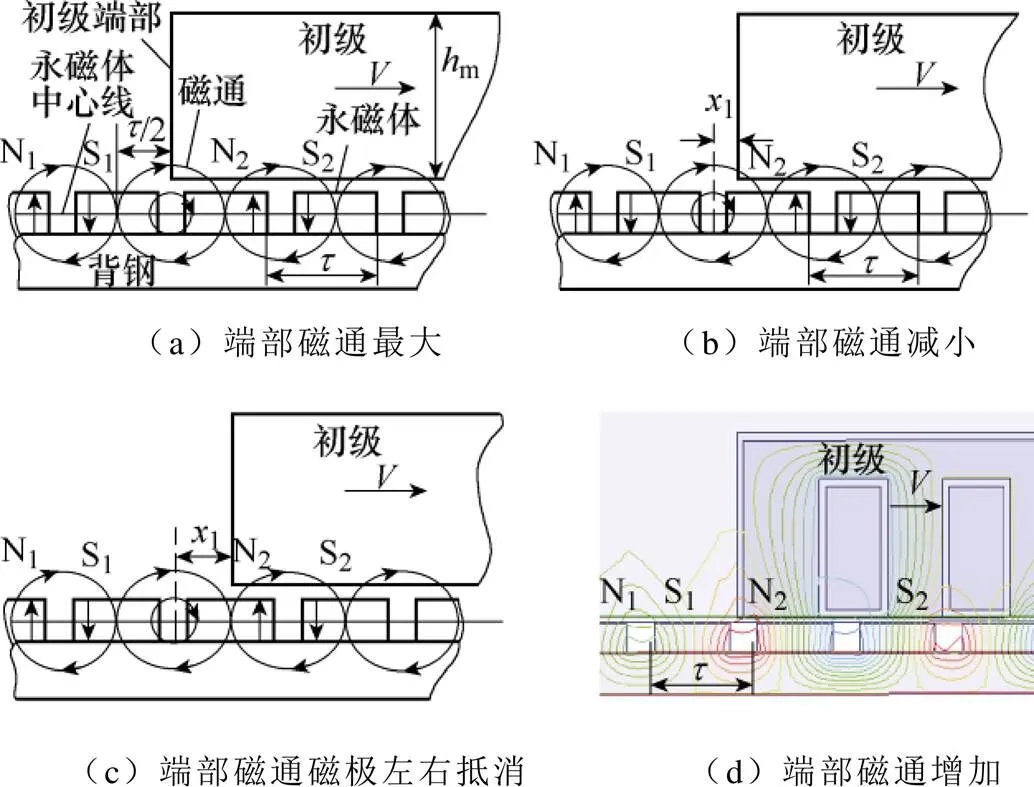
图1 端部磁通物理模型

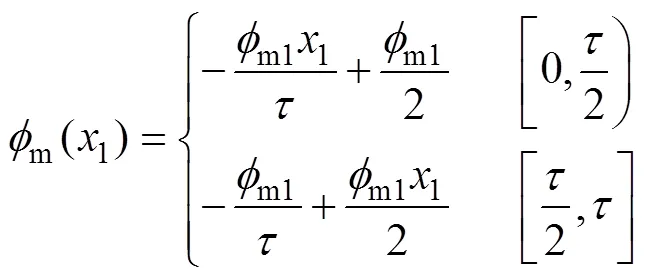
式中，m1为最大磁通；1为磁极q轴与动子纵向端面的距离；为极距。

电机初级两边纵向端面穿过的磁通具有相似的规律，磁通穿过初级两端存在相位差，相位差与初级长度有关。假设初级长度为，将1代入式（1），可求出穿过右边端面磁通。

1.2 端部气隙磁场推导

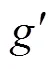
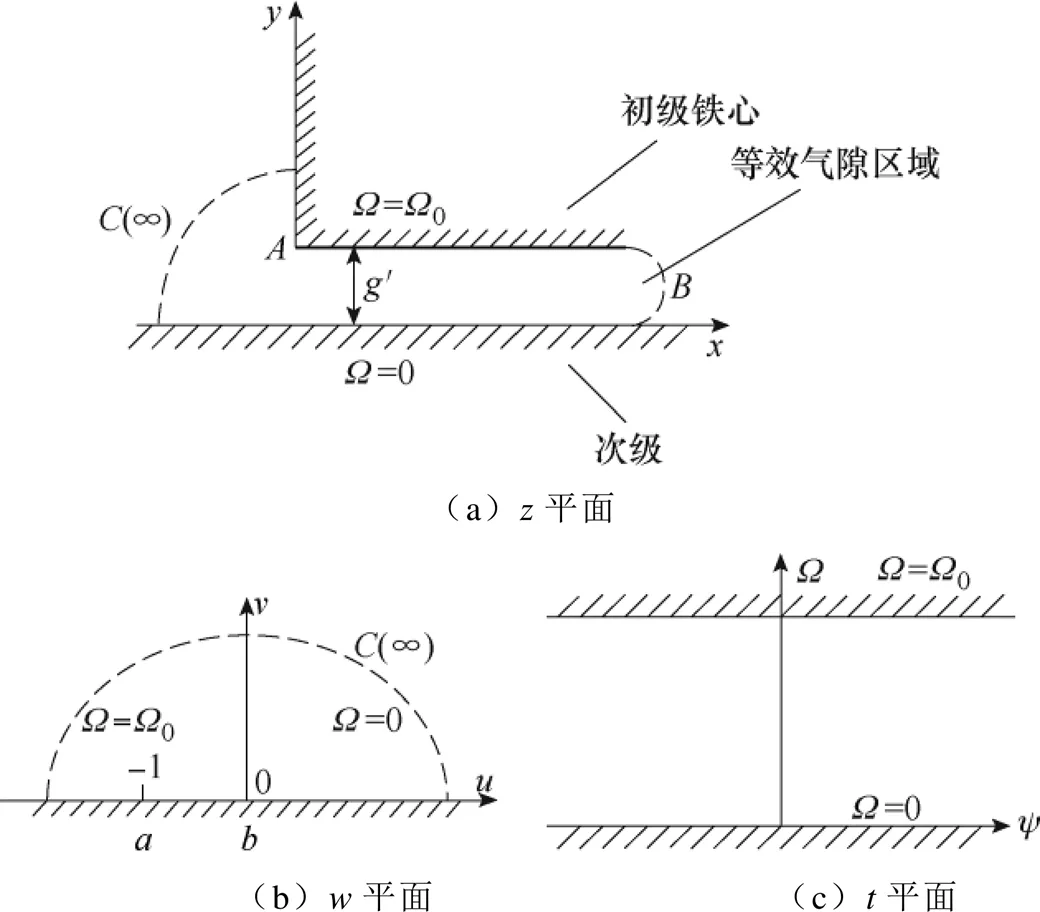
图2 端部效应分析模型

表1平面和平面的对应关系

Tab.1 Corresponding relations between z plane and w plane

平面跟平面的变换关系为

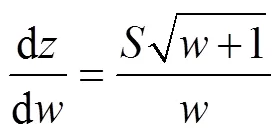
式中，等效为一个磁极的面积。

再对式（2）进行积分，可得

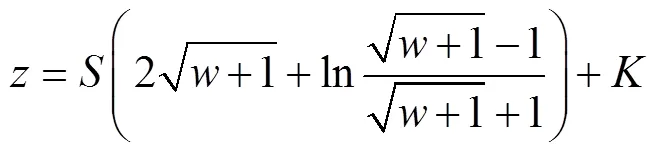
式中，为复常量。

再对式（3）进行对数变换，有

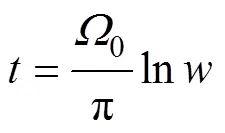
式中，0为铁心表面磁位。

可得极距内的磁感应强度为

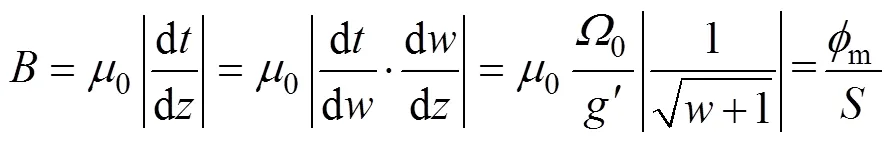
式中，0为真空磁导率。

由图1可知，磁路在满足磁路最短原则的情况下，穿过电机纵向端部的磁通还是会回到动子下方的磁极中，这也就使动子纵向边缘磁通变化引起动子间气隙储能发生改变，变化量[19]为

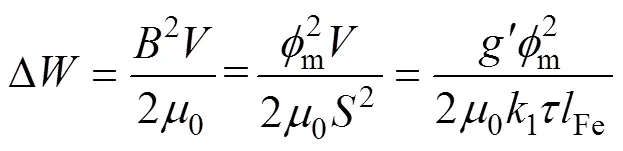
式中，m为永磁体向外磁路提供的磁通；1为磁通压缩系数；为一个极距下的气隙体积；Fe为动子铁心叠压厚度。

把式（1）代入式（6），瞬时气隙储能变化量Df为

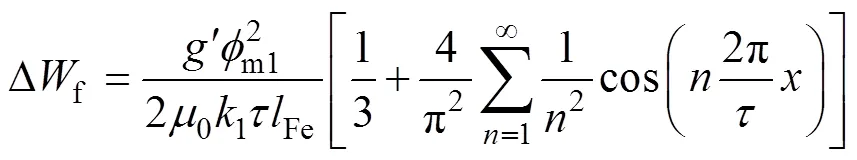
瞬时气隙储能变化量对动、定子之间相对位移进行求导，得到电机左侧推力波动表达式为

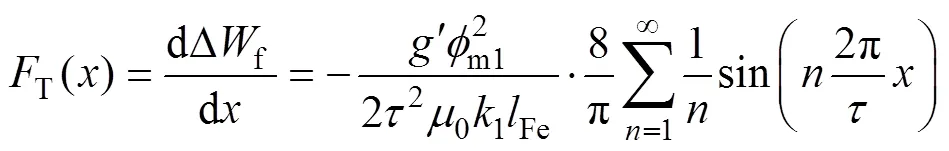
式（8）为左端的推力波动，而电机的右端产生的推力波动是对其动子进行阻碍，这里取阻碍端的

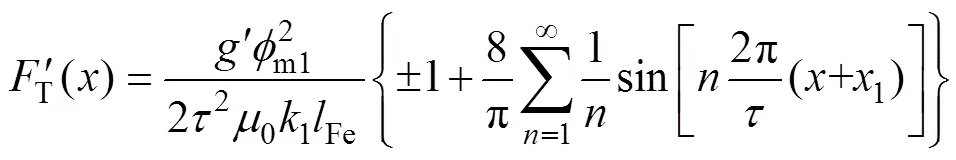
根据式（9）可知，由直线电机端部效应引起的磁阻力导致的推力波动可分为恒定分量与谐波分量，谐波分量是引起电机推力波动的一个很关键 因素。

2 磁极结构

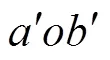
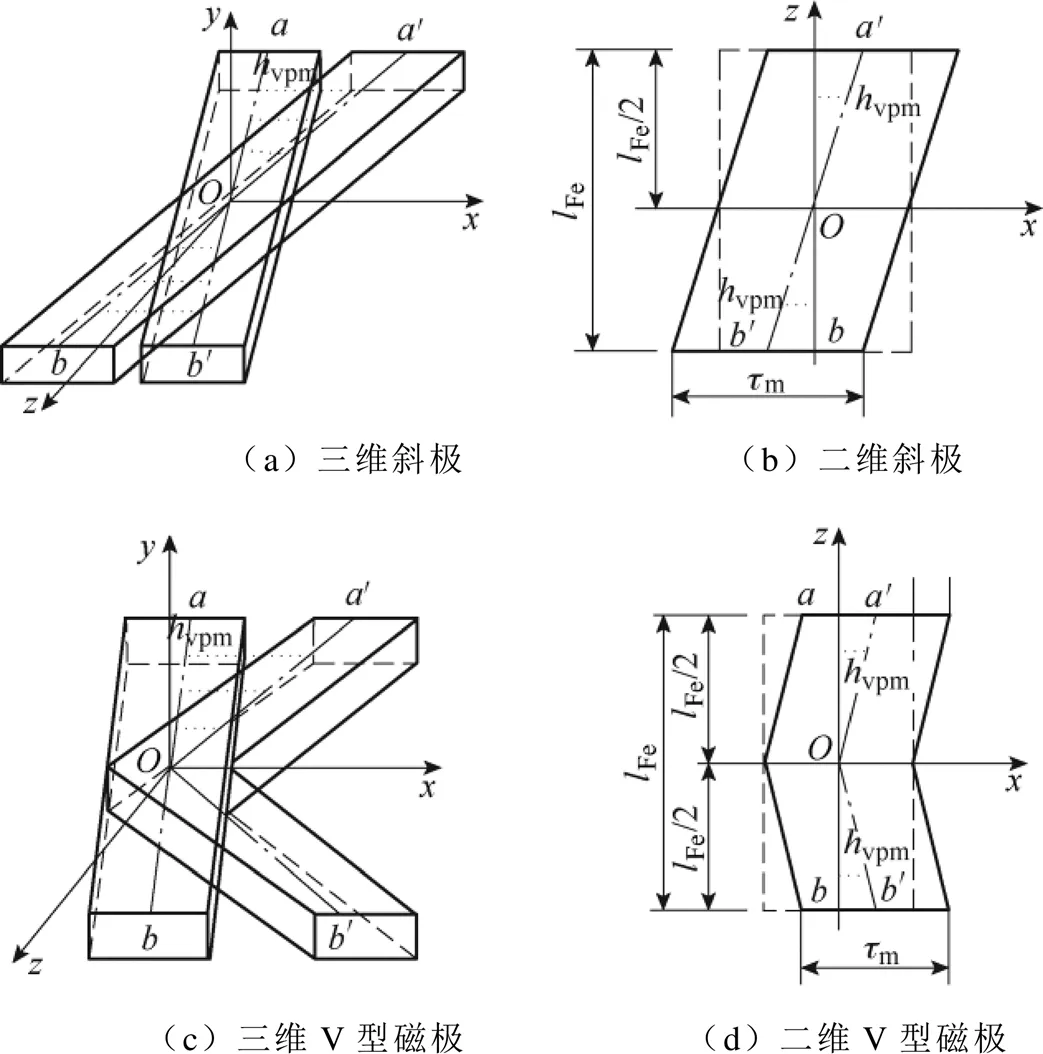
图3 磁极结构

sk为斜距与齿距的比值最，即

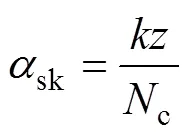
式中，c为齿槽数与极数的最小公倍数；为槽数；为常数。

sk为斜极参数，即

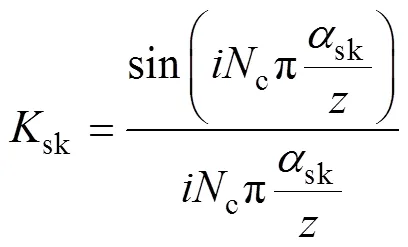
永磁体倾斜角度为

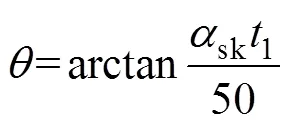
式中，1为电机槽距。

根据文献[17]，斜极磁阻力解析式为

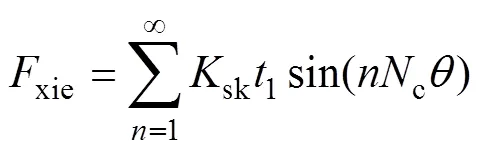
表2sk、斜极角度与vpm

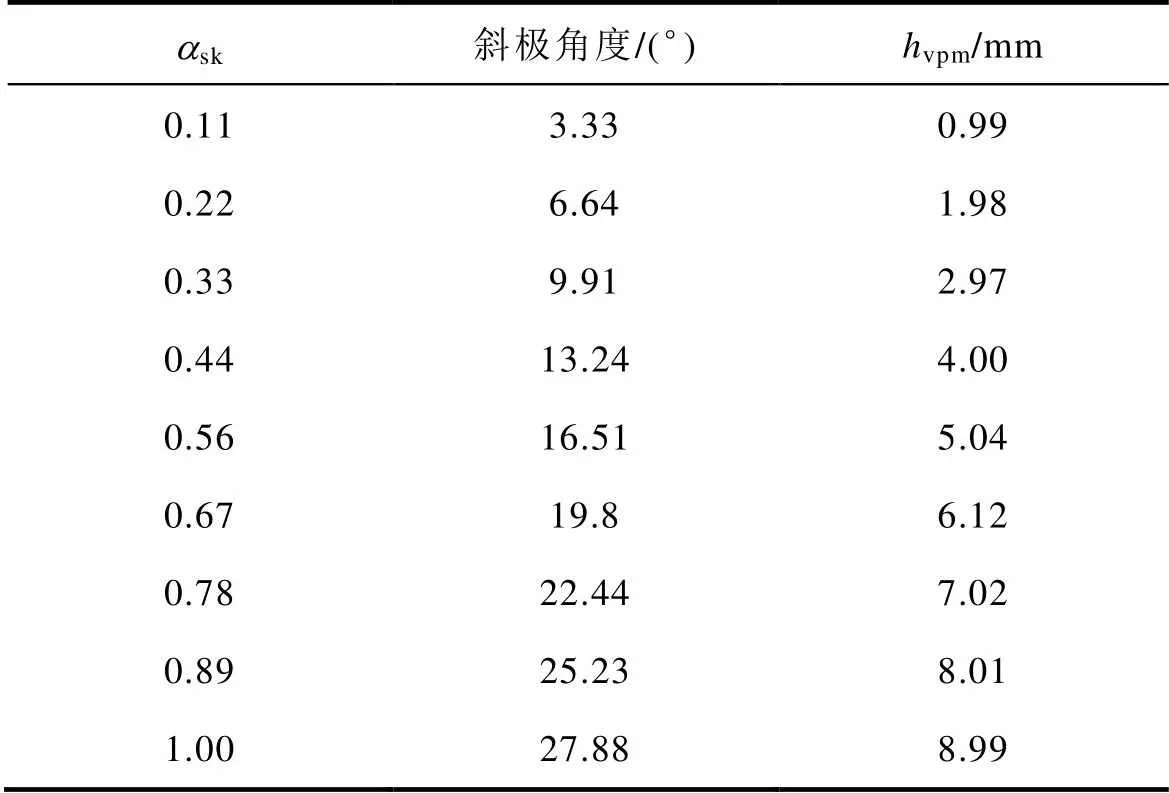
Tab.2 ask, oblique angle and hvpm

对式（9）进行积分，就可以得到V型磁极产生的磁通穿过动子纵向端面所产生的推力为

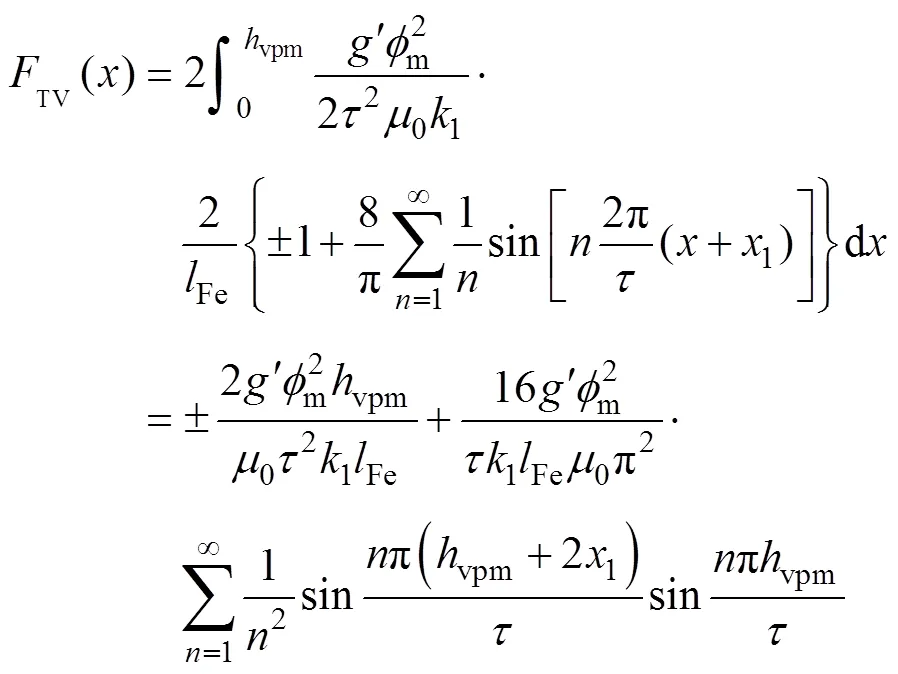
由式（8）可以推导出，单侧推力基波波动波长t，推力的2次谐波的波峰是基波的1/2，因此当谐波电角度相差90°时，端部效应的基波分量消除就可以有效减小推力的波动。基于以上分析可知，在进行磁极切分为三段时，要满足两端磁极面积之和等于中间磁极，这样所产生的谐波才可以相互抵消。磁极三段错位如图4所示。

当初级与次级固定时，引起推力波动谐波次数与相位关系固定。对式（14）的恒定部分进行忽略，可得次谐波引起的推力表达式为

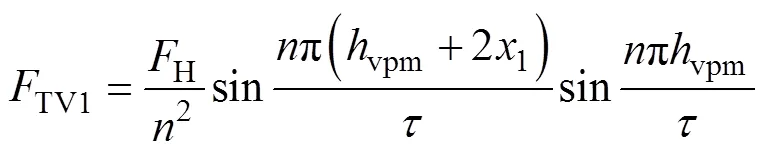
其中

V型三段永磁体磁极错位如图4a所示，把错位的距离D代入式（15），可以得到磁极错位后所产生的推力表达式为

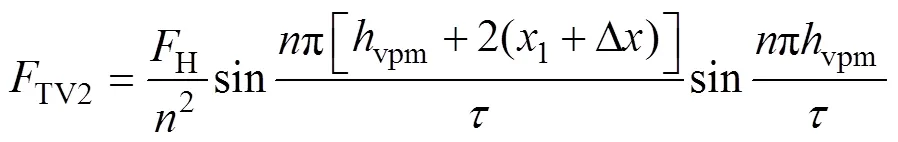
当D/2时，V型磁极中间与两端错位部分所产生谐波之和大小相同、方向相反，相互抵消。谐波次数为奇数时，错位磁级之间产生的谐波推力波动的相位相反，谐波推力的波动相互抵消；当谐波为偶数时，错位磁级之间产生的谐波推力相位相同，因此该次推力波动与整体磁极的波动相同，所以V型三段磁极在该错位距离无法削弱推力波动。

3 仿真结果分析

为了验证永磁体结构对于削弱推力波动的有效性与正确性，本文利用Ansoft Maxwell16.0建立永磁同步直线电机3D有限元模型，以推力波动较为显著的6槽7极开口槽永磁同步直线伺服电动机为例，电机参数见表3，在永磁体结构发生改变后进行磁极错位，可以得到永磁体结构发生改变后推力波动情况。

表3 永磁同步直线电机参数

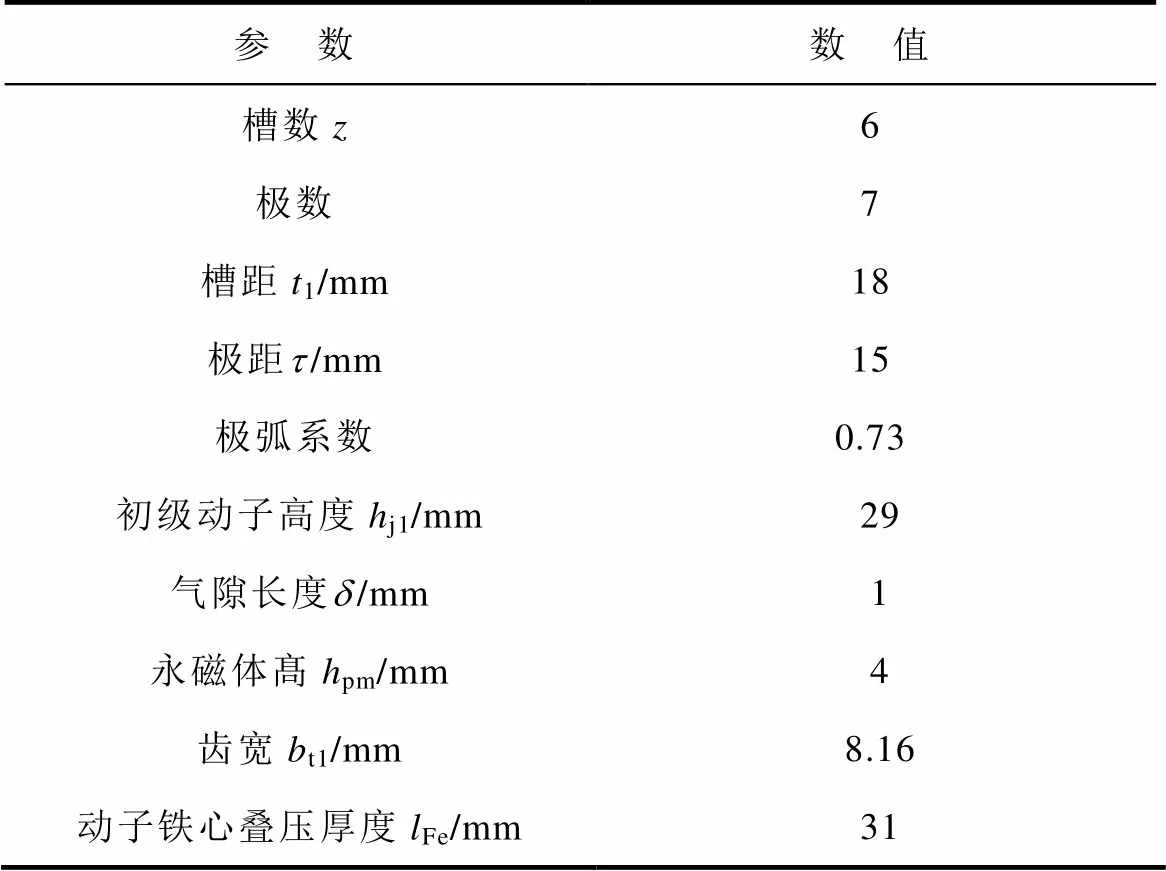
Tab.3 Permanent magnet synchronous linear motor parameters

6槽7极的直线电机极距为15mm，根据式（16）得到V型三段磁极之间相对位移为D=7.5mm，图5a是根据表3参数搭建的电机仿真模型。因为本文采用有限元法验证端部效应，所以在建模时为了证明优化方法对电机端部磁阻力的有效减小，电机初级模型两端进行无限延长，如图5b所示。

图5 平板型永磁同步直线电机

在电机初级无限长情况下，不同磁极有限元仿真后引起的齿槽推力波动如图6所示，V型磁极的齿槽推力为25N，传统磁极为22N，斜极为18N，V型三段磁极为10N，因此不同磁极结构对电机齿槽效应也具有不同的抑制效果。

推力仿真结果如图7所示，根据式（9）与图7b可知，正摆放磁极的推力波动基波次数为4，这与文献[2]中提到的谐波分量幅值分析一致，而在采用V型三段磁极后，4次谐波的幅值由23.31N下降到2.86N，6次谐波由14N下降为3.5N；而对于4次谐波的偶数倍次8次与16次谐波，因无法满足90°相位差，则8次谐波的幅值由2.3N增加到4.2N，16次谐波的幅值由2.7N增加到4N；电机总的推力波动由69N下降为12N。

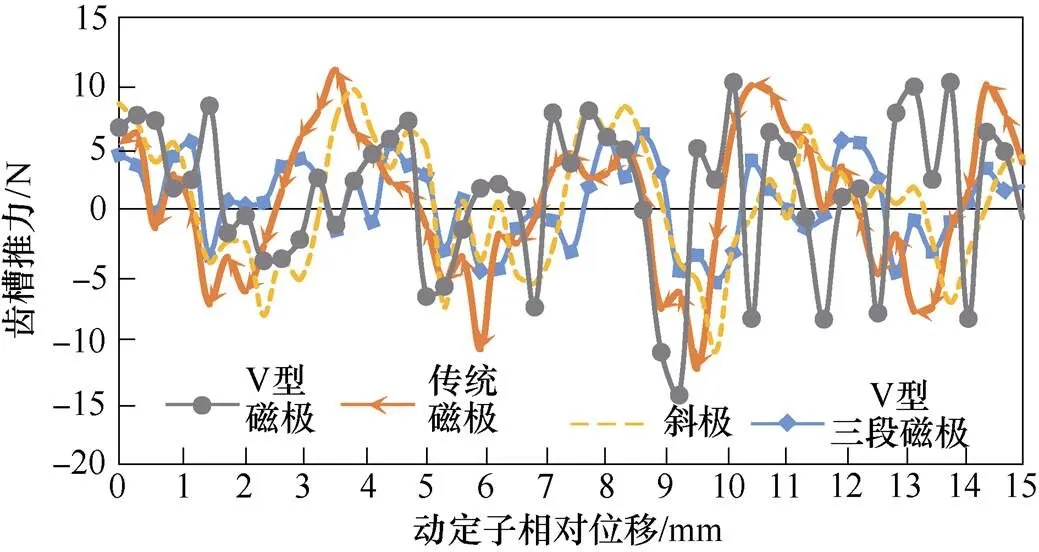
图6 不同磁极下齿槽推力波动

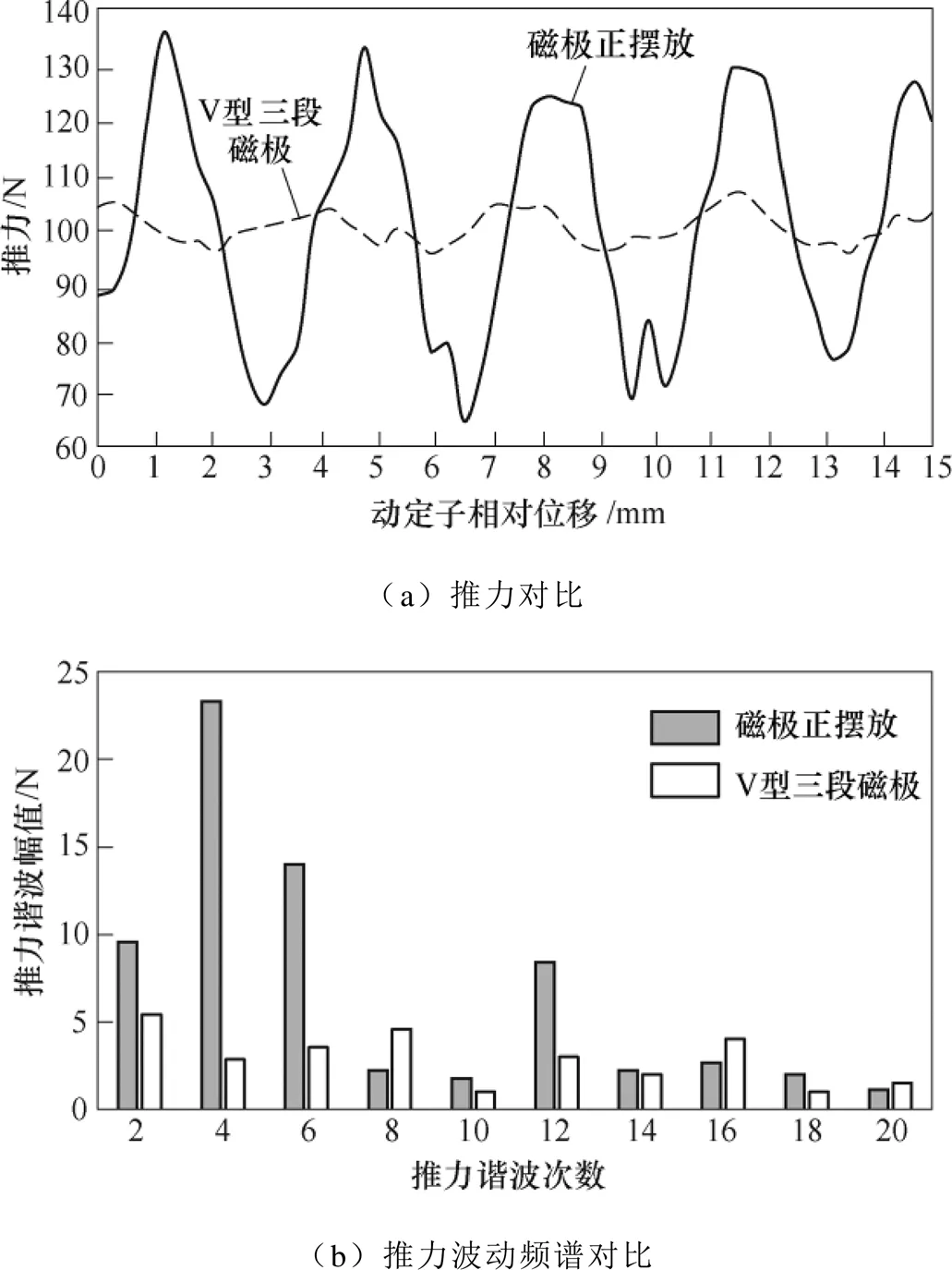
图7 推力仿真结果

四种磁极性能对比如图8所示，从图8b反电动势谐波分析可以看出，V型三段磁极谐波为3.83%，传统磁极为5.6%，斜极为5.73%，V型磁极为7.83%，电动势谐波均在误差允许范围之内。由图8c和图8d可知，四种磁极随着倾斜角度的改变，端部推力与法向力波动也发生改变，斜极的推力平均值与推力波动分别减小了68.81%与84.13%，V型磁极的推力平均值与推力波动分别减小34.78%与61.25%，传统磁极的推力平均值与推力波动分别减小54.96%与72.41%，V型三段磁极的推力平均值与推力波动分别减小32.4%与71.43%，对比不同磁极平均推力跟推力波动的数值可知，V型三段磁极在推力波动减小的情况下推力不发生大幅度削弱。

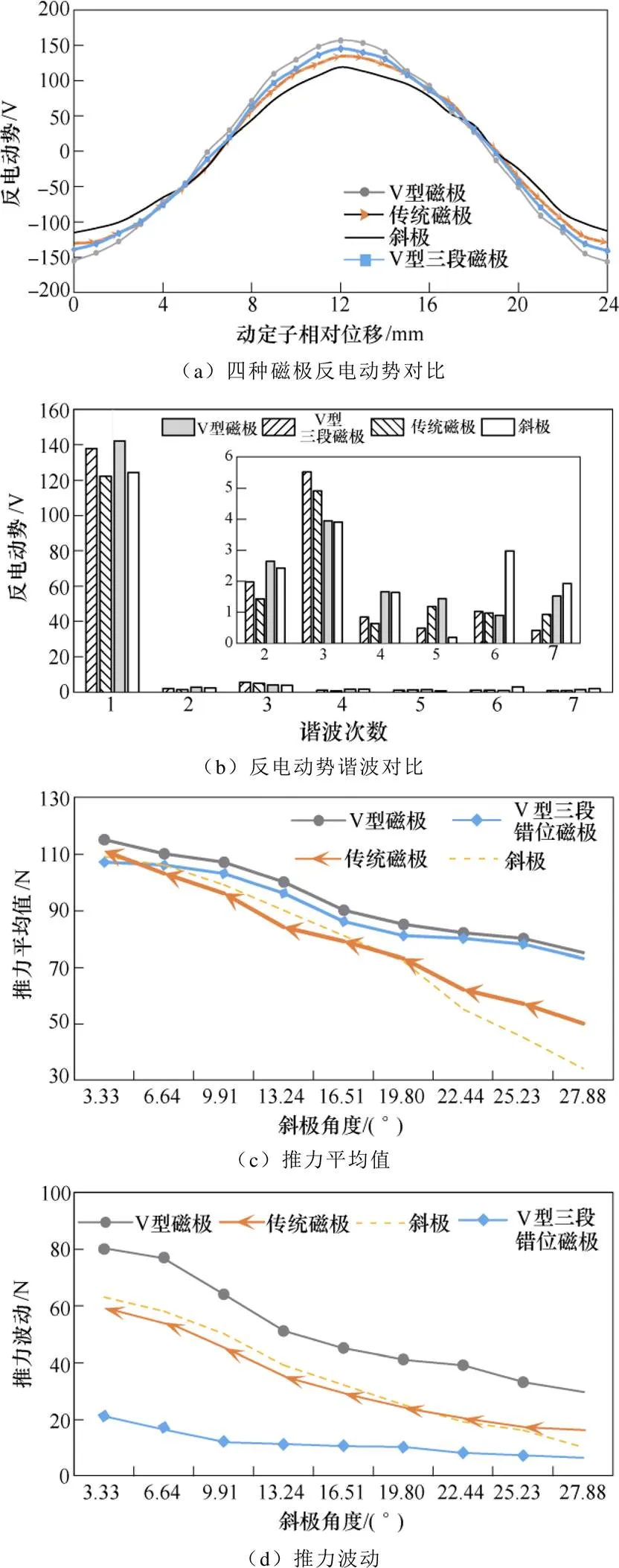
图8 四种磁极性能对比

磁极有限元仿真对比如图9所示，可知，四种不同永磁体的角度都取9.91°，斜极、传统磁极法向力与推力波动大小都近似相同。由图9a可知，采用V型磁极与V型磁极进行三段化处理前后法向力波动由58N减小到19N；由图9b可知，V型磁极与V型三段磁极的推力波动由64N减小到12N，平均推力由107N减小到103N，衰减3.7%。采用有限元法仿真可以证明，V型三段磁极可以在保证推力衰弱较小的情况下，更加有效地减小法向力与推力波动。

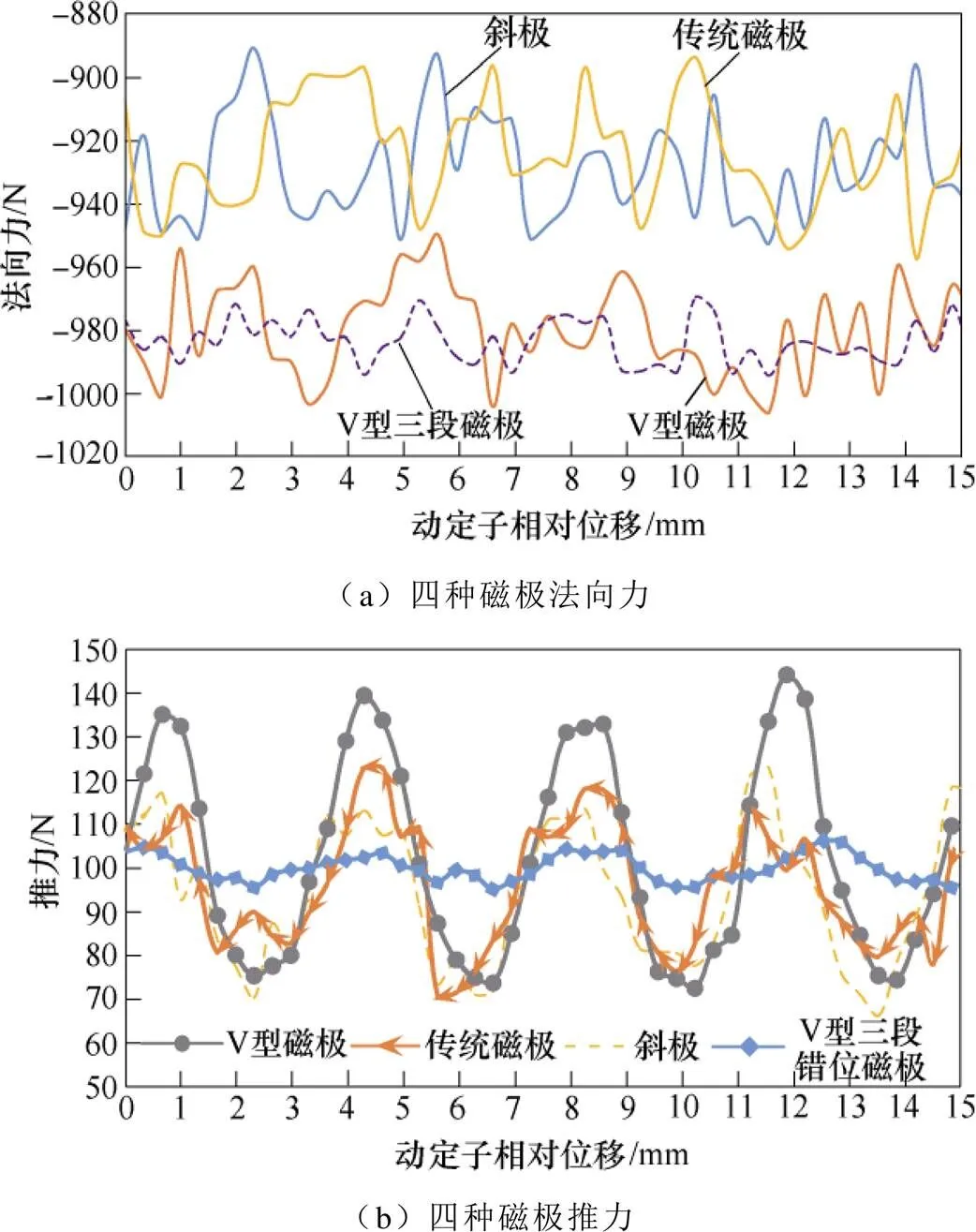
图9 磁极有限元仿真对比

4 仿真与实验结果分析

为了进一步对该方法的有效性进行验证，制作了一台6槽7极单边平板型永磁同步直线电机样机，并进行了推力波动的静态测试实验，其中，实验平台由进给装置及检测单元组成，如图10所示。检测单元包括光栅尺与读数头、BLR-SQA测力传感器与24V直流电源、KOLLMORGEN-AKD驱动器、驱动器配套分析软件与四种不同磁极等。把测力传感器装在辅助装置上，如图10b所示，由上位机对驱动器进行控制，调节电机光栅尺与读数头测量动子与定子的相对位移，相对位移为一个极距，用电机动子上安装的工装去顶测力传感器，测量出一个极距范围内的电机推力。图11为四种不同磁极下电机推力实验结果与V型三段磁极实验跟有限元仿真结果对比。

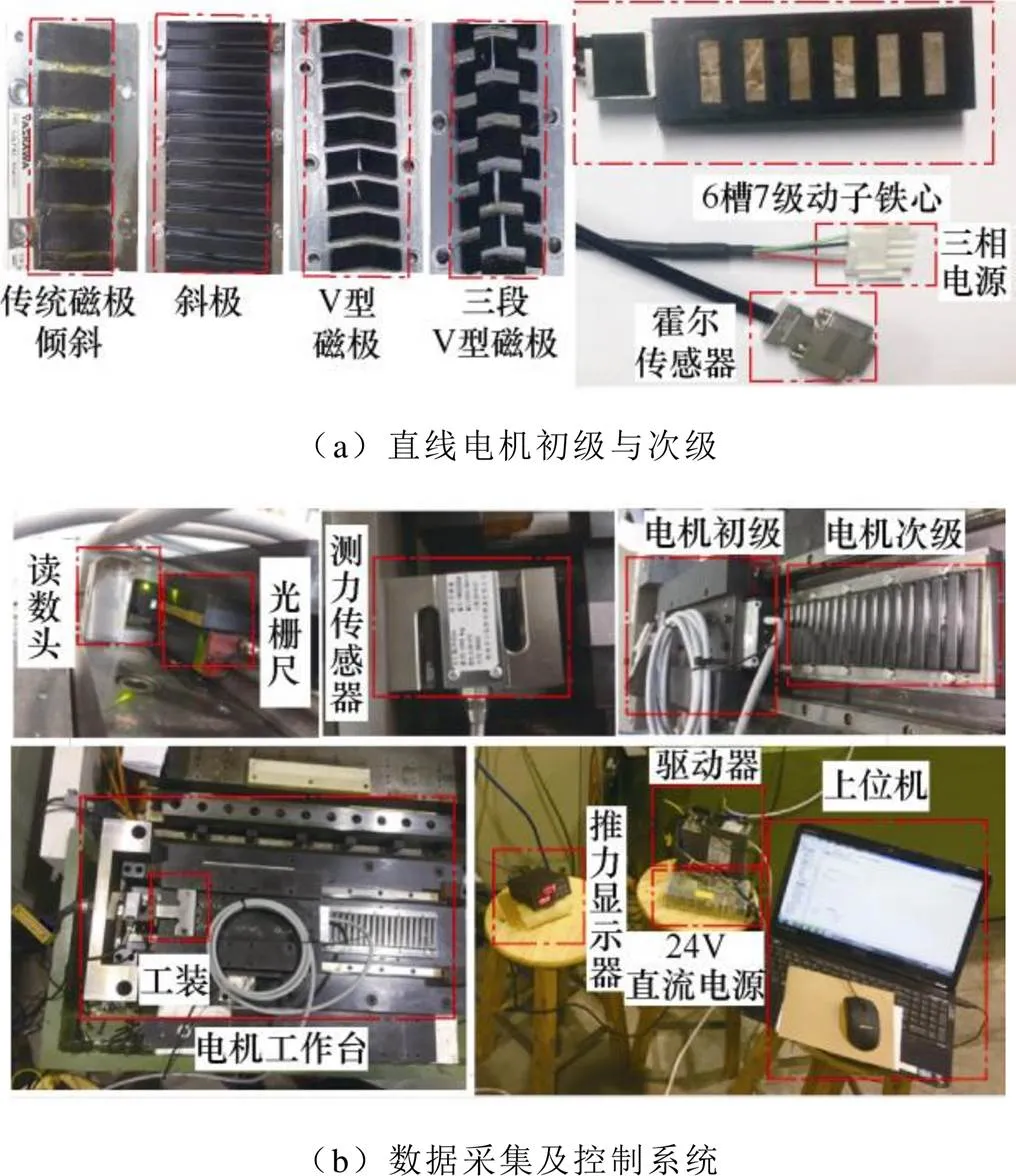
图10 推力实验检测平台

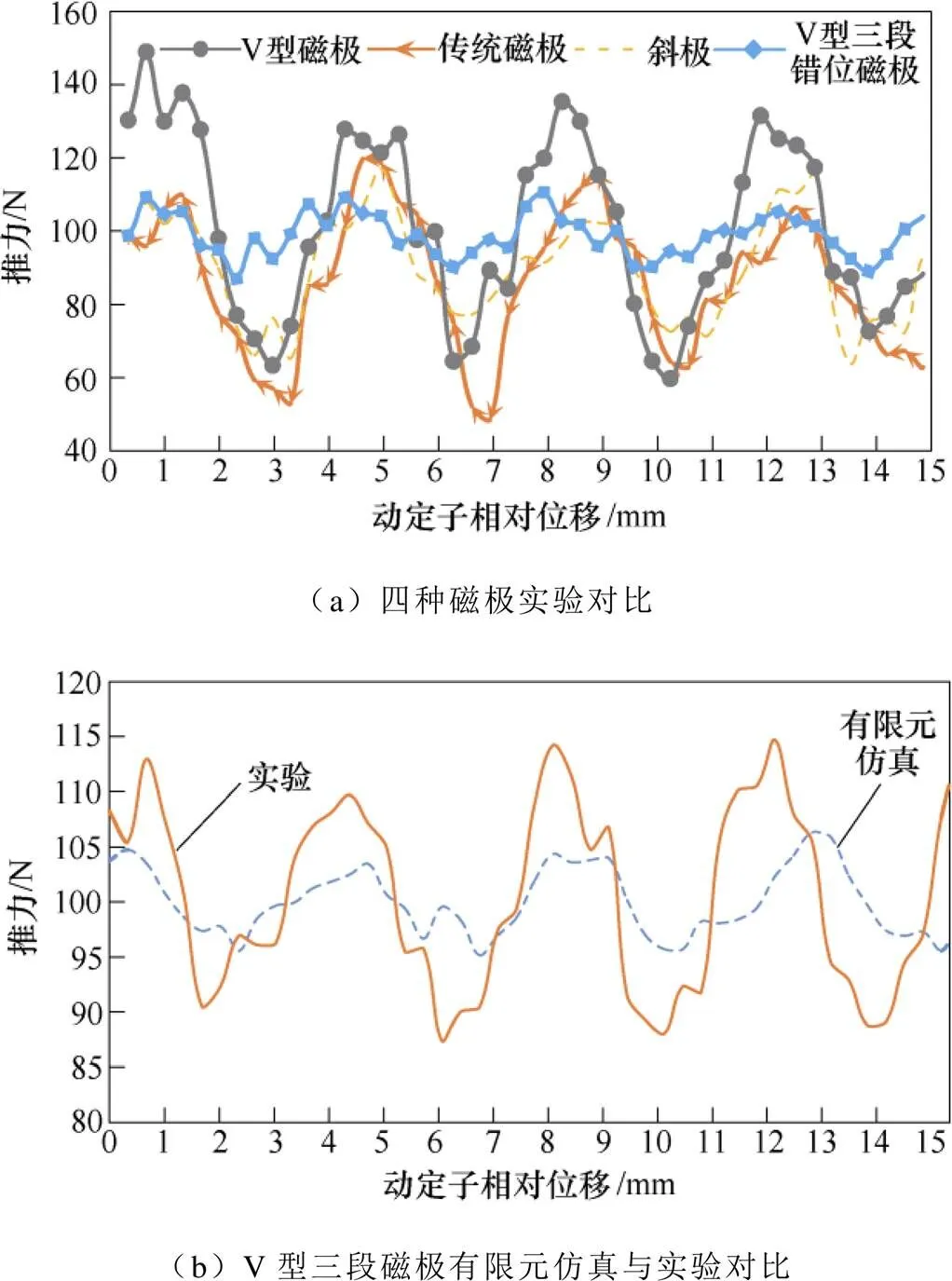
图11 实验结果

由图11可知，实验测量结果与有限元仿真结果存在一定的偏差，原因有：①磁极结构发生变化后次级的安装存在误差；②检测单元的客观性误差；③没有考虑电流谐波；④V型磁极三段式结构在磁极安装上错开的距离存在偏差；⑤磁极充磁不均匀等。

5 结论

本文研究了不同结构的永磁体对永磁同步直线电机推力波动的影响，在四种不同磁极下最大限度地削弱推力波动并且使推力不发生大幅度减小，通过理论分析、有限元仿真和实验验证，得到如下结论：

1）经过许克变换法的分析，推出永磁同步直线电机端部磁阻力引起的推力波动解析表达式，并且根据表达式可得到端部引起推力波动的原因。

2）根据不同的磁极结构，在推力波动较小的情况下，保持推力不发生大幅度减小。而V型三段磁极错位与其他磁极相比较优势在于削减推力波动更加有效，并且推力衰减情况较小。

3）以一台6槽7极的永磁直线伺服电动机为例，可以得到V型三段磁极错位的有限元仿真结果与实验基本一致，证明了运用V型磁极三段错位法可以有效削减端部磁阻力引起的推力波动。

[1] 夏加宽, 沈丽, 彭兵, 等. 齿槽效应对永磁直线伺服电机法向力波动的影响[J]. 中国电机工程学报, 2015, 35(11): 47-53.

Xia Jiakuan, Shen Li, Peng Bing, et al. Influences of cogging effects on normal force ripple in permanent magnet linear servo motors[J]. Proceedings of the CSEE, 2015, 35(11): 47-53.

[2] 彭兵, 张囡, 夏加宽, 等. 永磁直线电机端部效应力的解析计算[J]. 中国电机工程学报, 2016, 36(2): 547-553.

Peng Bing, Zhang Nan, Xia Jiakuan, et al. Analytical calculation for end effect forces in permanent magnet linear motors[J]. Proceedings of the CSEE, 2016, 36(2): 547-553.

[3] 崔鹏, 张锟, 李杰. 基于许-克变换的悬浮电磁铁力与转矩解析计算[J]. 中国电机工程学报, 2010, 30(24): 129-134.

Cui Peng, Zhang Kun, Li Jie. Calculation of electro magnetic force and torque of suspension electro- magnet based on schwarz-christoffel transform[J]. Proceedings of the CSEE, 2010, 30(24): 129-134.

[4] 秦伟, 范瑜, 徐洪泽. 高温超导运动磁场电磁Halbach初级结构直线感应磁悬浮电机[J]. 电工技术学报, 2018, 33(23): 5427-5434.

Qin Wei, Fan Yu, Xu Hongze. A linear induction maglev motor with HTS traveling magnetic electro- magnetic Halbach array[J]. Transactions of China Electrotechnical Society, 2018, 33(23): 5427-5434.

[5] Chen Meiyung, Lu ian-Shiun. High-precision motion control for linear permanent agnet iron core synchro- nous motor drive in position platform[J]. IEEE Transa- ction on Industrial Informatics, 2014, 106(1): 99-108.

[6] 卢琴芬, 程传莹, 叶云岳, 等. 每极分数槽永磁直线电机的槽极数配合研究[J]. 中国电机工程学报, 2012, 32(36): 64-78.

Lu Qinfen, Cheng Chuanying, Ye Yunyue, et al. Slot pole number combination research of pm linear motor with fractional slots per pole[J]. Proceedings of the CSEE, 2012, 32(36): 64-78.

[7] 罗俊, 寇宝泉, 杨小宝. 双交替极横向磁通直线电机的优化与设计[J]. 电工技术学报, 2020, 35(5): 991- 1000.

Luo Jun, Kou Baoquan, Yang Xiaobao. Optimization and design of dual-consequent-pole transverse flux linear machine[J]. Transaction of China Electro- technical Society, 2020, 35(5): 991-1000.

[8] Xia Jiakuan, Li Weiyang, Li Shen. Skew and end- teeth optimization in reduce permanent magnet linear synchronous motor normal force fluctuation[J]. Advanced Materials Research, 2011, 383-390: 4853-4859.

[9] Huang Rui, Zhou Jianpei, Kim G T. Minimization design of normal force in synchronous permanent magnet planar motor with halbach ray[J]. IEEE Transactions on Magnetics, 2008, 44(6): 1526-1529.

[10] 宁建荣, 沈丽, 曹景全, 等. 减小法向力波动永磁同步直线电动机优化设计[J]. 微电机, 2012, 45(9): 43-47.

Ning Jianrong, Shen Li, Cao Jingquan, et al. Opti- mization design of permanent magnet linear syn- chronous motor for reduce normal force fluctuation[J]. Micro Motor, 2012, 45(9): 43-47.

[11] 凌志健, 赵文祥, 吉敬华. 高推力永磁直线作动器及关键技术综述[J]. 电工技术学报, 2020, 35(5): 1022-1035.

Ling Zhijian, Zhao Wenxiang, Ji Jinghua. Overview of high force density permanent magnet linear actuator and its key technology[J]. Transaction of China Elec- trotechnical Society, 2020, 35(5): 1022-1035.

[12] 韩雪岩, 祁坤, 张哲, 等. 永磁同步直线电机磁阻力分析及抑制措施[J]. 电工技术学报, 2015, 30(6): 70-76.

Han Xueyan, Qi Kun, Zhang Zhe, et al. Analysis and suppression measures of magnetic resistance force in permanent magnet linear synchronous motors[J]. Transaction of China Electrotechnical Society, 2015, 30(6): 70-76.

[13] 寇宝泉, 张赫, 郭守仑, 等. 辅助极一体式永磁同步直线电机端部定位力抑制技术[J]. 电工技术学报, 2015, 30(6): 106-113.

Kou Baoquan, Zhang He, Guo Shoulun, et al. End effect detent force reduction for permanent magnet linear synchronous motors with auxiliary poles one- piece structure[J]. Transaction of China Electro- technical Society, 2015, 30(6): 106-113.

[14] 彭兵, 宋得雪, 张囡, 等. V-型端齿削弱永磁直线电机端部磁阻力波动方法[J]. 中国电机工程学报, 2016, 36(14): 3940-3947.

Peng Bing, Song Dexue, Zhang Nan, et al. An end effect detent force reduction method of V-shaped end teeth in permanent magnet linear motors[J]. Pro- ceedings of the CSEE, 2016, 36(14): 3940-3947.

[15] 张静, 余海涛, 施振川. 一种波浪发电装置用低速双动子永磁直线电机运行机理研究[J]. 电工技术学报, 2018, 33(19): 4553-4562.

Zhang Jing, Yu Haitao, Shi Zhenchuan. Research on a tubular linear permanent magnet machines with dual translators for low speed wave energy conversion[J]. Transaction of China Electrotechnical Society, 2018, 33(19): 4553-4562.

[16] 许孝卓, 孙震, 汪旭东, 等. Halbach交替极永磁同步电机直线电机特性分析[J]. 电工技术学报, 2019, 34(9): 1825-1833.

Xu Xiaozhuo, Sun Zhen, Wang Xudong, et al. Charac- teristic of a novel permanent magnet linear synchronous motor with Halbach array consequent pole[J]. Transaction of China Electrotechnical Society, 2019, 34(9): 1825-1833.

[17] Shin J, Watanabe R, Koseki T, et al. The design for cogging force reduction of a double transverse flux permanent magnet linear synchronous motor[J]. IEEE Transaction on Industrial Informatic, 2011, 50(11): 41-69.

[18] 宗开放, 赵吉文, 宋俊材, 等. 基于V型线圈永磁同步直线电机推力波动抑制[J]. 中国电机工程学报, 2019, 39(22): 6736-6746.

Zong Kaifang, Zhao Jiwen, Song Juncai, et al. Thrust ripple reduction based on V-coil permanent magnet synchronous linear motors[J]. Proceedings of the CSEE, 2019, 39(22): 6736-6746.

[19] 彭兵, 李丽萍, 张囡, 等. 双V型结构削弱永磁直线电机磁阻力波动方法[J]. 电工技术学报, 2017, 32(22): 108-114.

Peng Bing, Li Liping, Zhang Nan, et al. A method for reduce detent force fluctuation by double V-shaped structure in permanent magnet linear motor[J]. Transaction of China Electrotechnical Society, 2017, 32(22): 108-114.

[20] 彭兵, 刘铁法, 张囡, 等. 凹型端齿削弱永磁直线电机端部力波动方法[J]. 电工技术学报, 2015, 30(7): 119-124.

Peng Bing, Liu Tiefa, Zhang Nan, et al. A method for reducing the end effect force fluctuation by the concave profile end-tooth in permanent magnet linear motors[J]. Transaction of China Electrotechnical Society, 2015, 30(7): 119-124.

[21] 夏加宽, 沈丽, 彭兵, 等. 磁极错位削弱永磁直线伺服电动机齿槽法向力波动方法[J]. 电工技术学报, 2015, 30(24): 11-16.

Xia Jiakuan, Shen Li, Pen Bing, et al. The magnet stagger method to weaken the cogging effect normal force ripple of permanent magnet linear servo motor[J]. Transaction of China Electrotechnical Society, 2015, 30(24): 11-16.

Method for Weakening Thrust Fluctuation of Permanent Magnet Linear Motor Based on V-Shaped Three-Stage Magnetic Pole Misalignment

1123

（1. College of Information Engineering Xiang Tan University Xiangtan 411105 China 2. Shanghai Ceyong Automation Technology Co. Ltd Shanghai 200120 China 3. Weisheng Electric Co. Ltd Xiangtan 411105 China）

The 6-slot, 7-pole single-sided flat-plate permanent magnet synchronous linear motor (PMLSM) generates thrust fluctuations during operation, resulting in poor machining accuracy. This paper proposes an optimization method combining magnetic pole misalignment and V-shaped magnetic poles to improve its performance. Firstly, the end magnetic field is analyzed by the Huck transform method to obtain the analytical expression of the total thrust fluctuation caused by the end effect. Then the Fourier coefficients in the analytical formula are analyzed, and the main harmonic order of thrust fluctuation caused by the end effect is obtained. Through the finite element simulation of a variety of permanent magnet structures, the method of V-shaped three segment dislocation pole is obtained from the force characteristics. When the phase difference between the two poles and the middle pole is 90 degrees, the thrust fluctuation can be effectively reduced. Finally, a prototype was made based on this method. The finite element results and prototype experiments verify the feasibility of this method, which provides a guidance for the optimal design of single-sided flat PMLSM.

V-shaped three-stage magnetic pole dislocation, Huck transform method, cogging magnetic resistance, end normal force fluctuation, permanent magnet synchronous linear motor, finite element simulation

10.19595/j.cnki.1000-6753.tces.191786

TM351-359.4

兰志勇 男，1980年生，博士，教授，研究方向为大功率永磁同步电机设计及优化、无刷直流电机设计及优化、精密伺服驱动器的研究与开发等。E-mail: lanlanzhiyong@ 163.com

谢 斌 男，1995年生，硕士研究生，研究方向为永磁同步直线电机设计与优化。E-mail: 2455541573@qq.com（通信作者）

国家自然科学基金（51507148）和风力发电机组及控制湖南省重点实验室开放研究基金（2016FLFDYB02）资助项目。

2019-12-20

2020-02-23

（编辑 崔文静）