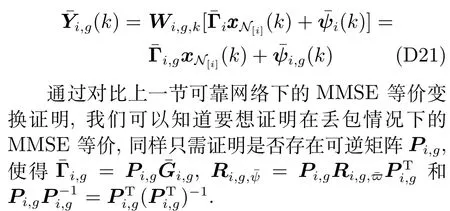工业物联网中的精确时钟同步:网络化控制理论观点
2021-08-28徐小权唐晓铭黄庆卿李永福
王 頲 徐小权 唐晓铭 黄庆卿 李永福
适合关键业务型工业物联网(Industrial internet of things,IIoT) 应用的工业无线传感器网络(Industrial wirelesssensornetworks,IWSN) 需要部署在典型严酷工业环境中,具有关键要求[1].在IIoT 中,数据融合、能量管理、传输调度、定位和追踪协议要求所有的节点运行在公共的时间基准[2].通过使用统计信号处理观点,很多时钟同步协议归类为参数估计问题,已经在不同的网络随机延迟分布下,评估了一些经典协议的性能[3].由于IWSN中存在许多不可靠的因素,例如包延迟、丢失、节点失效等,导致这些同步协议算法的性能大大地降低,甚至算法失败.特别指出,国内学者针对时钟同步问题的前沿理论研究,可参见文献[4].国际前沿研究中,一致性算法[5−6]在分析中没有考虑包延迟,因此,在收敛的时钟参数中产生了大的均方误差.在文献[7] 中,鲁棒平均时间同步(Robust average time synchronization,RoATS) 提出来相应于边界通信延迟,以鲁棒的方法调节节点的时钟频率和时钟偏移.在文献[8] 中,提出一组基于2 阶一致性的随机时钟同步协议.已经证明,在这样的方法下,可以总是调节算法参数,且在概率均方意义下达到时钟同步.然而,一致性算法[7−8]不能在分析中量化消息延迟的影响,特别是包延迟.作为耦合状态模型的相对时钟模型依赖于交互平均以达到同步补偿或协作控制过程.因此,已经存在的协议和一致性平均方法受限于网络规模,随着网络规模的扩展,时钟同步收敛性能将下降.
IIoT 在规模网络下分布式精确时钟同步问题仍然是处于目前的研究热点.作为耦合状态模型的相对时钟状态模型依赖于协作控制过程.受限于网络尺寸的一致性时钟同步方法的收敛率研究集中在收敛性(稳定性),难以量化和分析收敛率,特别是对于不可靠网络.
当存在消息延迟时(固定时延),用于文献[2] 的卡尔曼滤波(Kalman filtering) 导出了用于时钟偏移追踪的消息传递方法(双向信息交换).事实上,文献[2] 的时钟模型具有新的不同本质(节点的时钟状态依赖于状态空间模型度量下自身节点状态的噪声扰动).文献[2] 的绝对时钟模型建模为解耦状态模型,但量测模型仍然是绝对状态的辅助量测过程.事实上,存在状态耦合关系.根据现代控制理论观点,通过分析文献[2],发现无法满足系统的能观测性(更坚实的理论依据参见附录A).因此本文首先针对绝对时钟模型的能观测性的问题.
考虑包丢失(过度的延迟被认为是丢失) 和节点失效作为节点量测信息丢失,为了量化丢失的量测信息的影响,已经广泛地采用两类通道模型:1) 独立同分布(Independent and identically distributed,i.i.d.) 模型,建模包丢失过程为一个独立同分布过程[9];2)在马尔科夫模型下,包处理过程描述为二元马尔科夫链[10].
在独立同分布(i.i.d.) 模型下,文献[2] 和文献[11−13] 集中在间隙卡尔曼滤波的稳定性,此时仅一个传感器传输它的原始量测,且存在一个临界丢包率.在临界丢包率以上,状态估计误差协方差矩阵的均值将发散为无穷[9].在文献[9] 中,也给出了临界丢包率的上界和下界.对于一般的向量系统,众所周知难以显式地表达临界丢包率.也是源于处理文献[9] 的局限性,文献[13] 中对于一步可观测系统下界可显示为“紧”的,包括文献[12] 中所示的非退化系统.然而,文献[14] 中的一个反例显示临界丢包率严格地位于下界和上界之间.
针对含多传感器的网络化状态估计问题,许多研究者广泛研究了针对不同传感器,约束于可能不同的包丢失情形[15−20].在文献[21]中,开发了一种新的回归矩阵技术,用于研究针对于MMSE (Minimum mean square error) 估计器的必要与充分稳定条件,它适用于单一传感器和多传感器情形.
在“工业物联网”的前期研究中,文献[4] 针对不可靠量测的“相对时钟模型”,基于适合在线运算的Tubes-MPC (Model predictive control) 控制方法完成“指数收敛性”量化分析.文献[1] 已经开展的工业物联网TDMA (Time division multiple access) 确定性调度算法中,维护高可靠性的时间精度具有重要意义.文献[22] 作为本文重要研究背景的“工业物联网”精确时钟同步的紧时隙需求,本文提出的MMSE 等价变换能观测性观测模型符合噪声量测的实际应用模型,对文献[22] 的理想观测器进行了深度分析扩展.
本文的建模与适用性:1) 建模特点:文献[2]的网络拓扑来源于实际的网络应用拓扑结构(如工业无线ISA100、WirelessHart、WIA-PA 中的Mesh 网络拓扑),具体的网络协议可参考前期文献[22−24] 和文献[25].2) 协议特点:对于本文及文献[2] 的分布式网络拓扑(全分布、短时延Cyber-Physical 环境要求),具体应用于无线Mesh网络(Wirelessmeshnetwork,WMN)[23−24],将在工业物联网TDMA独立时隙间实现无冲突的数据传输,以有效提高资源利用率[25].
为了不依赖于特定的相对参考节点或网络结构,文献[2] 中绝对状态模型建模为绝对状态空间模型,状态相对于本地时钟的理想状态(状态空间“0”点).本文通过对文献[2] 的“能观测性”的分析,建立了MMSE 等价变换的能观测性观测模型,观测模型的能观测性是系统状态确定性估计的必要条件.由提出的新的解耦观测模型,建立了基于文献[2,15] 的规模网络的修正的卡尔曼滤波,建立了时钟同步的量化分析的收敛条件.
本文的主要贡献是:
1)基于前期的研究[4,22,26−27],本文基于卡尔曼滤波的精确时钟同步研究,从“网络化控制理论观点”准确定位文献[2] 的研究实质(参见命题1),分析了双向信息交换的物理量测模型和在BMU (Basic measurement unit) 下建立的适用于大规模网络的“能观测性”精确量测模型.
2) 通过使用MMSE 等价能观测性量测模型,能够得到确定性的绝对状态的估计值(基于理想状态(1,0)).能够解除节点间的状态耦合与控制耦合.时钟同步问题被转化为对于本地时钟理想状态(1,0) 的分布式卡尔曼滤波精确设定点状态追踪问题.
3) 通过MMSE 等价能观测性的状态解耦的量测模型,实现了对工业物联网的时钟同步精度的量化分析.
注1.本文使用有N个传感器节点{S1,S2,···,SN}的网络为研究对象,对于任意节点Si,i∈{1,2,···,N}.Ni表示Si的邻居节点集合,Ni={Ni(j)=mj|m1,···,mj,···,m|Ni|}(mj∈Ni,j∈{1,···,|Ni|});Nj表示Sj的邻居节点集合,Nj={Nj(o)=mo|m1,···,mo,···,m|Nj|}(mo∈Nj,o∈{1,···,|Nj|}).N[i]表示包含Si及其邻居节点的局部子系统,N[i]={Ni,i},元素个数|N[i]|=|Ni|+1.(·)M×N表示任意M行N列的矩阵.
注 2.不可靠量测丢包变量定义,参见表1.

表1 不可靠量测丢包变量定义Table 1 Definition of unreliable packet loss variables
1 系统解耦状态模型
文献[2] 中,考虑了传感器时钟偏斜和累积时钟偏移的演化模型


为了达到全网的时钟同步,所有节点的时钟读数c i(k) 必须被调节为公共的值.假定UTC(Universaltimecoordinated)作为准确的参考时间,也就是β(k)=1 和ϑ(k)=0,并且基于离散时钟读数模型ci(k)=k∆τ0+ϑ(k −1)+[β(k−1)−1]∆τ0,全网时钟同步任务将对应于UTC追踪时变的时钟偏斜{βi(k)}和累积偏移{ϑi(k)}.对比于文献[2],假定节点S1为具有准确时钟的参考节点实现绝对时钟量测模型是不合理的(更坚实的理论依据参见附录A).方程(1) 中的节点时钟状态建模源于自身节点扰动的物理模型(而不依赖于其他节点),称方程(1) 为绝对时钟状态模型.
2 本地能观测性解耦观测器
2.1 大规模系统本地观测器
现有研究均采用相对时钟状态模型,及相对时钟量测模型以获取时钟状态的观测值.因采用相对时钟模型,则收敛性能依赖于网络规模.本节将讨论我们提出的从文献[2] 的绝对状态空间模型出发,构建能观测性系统量测方程的新方法.
节点Si和它的邻居节点Sj之间的双向时间戳交换如图1.不同于文献[2],我们在量测关系上平等地对待Si和Sj,例如式(10),同时存在和
事实上,IWSN 有一系列的不可靠的因素,会对时间戳丢失产生影响.因此,我们必须考虑时间戳丢失的影响(全面的丢包假设参见文献[21,28];可扩展说明参见第3 节).在一轮双向信息交换过程中(如图1 所示),无论哪一部分的时间戳丢失,它将影响时间戳交换轮次的成功,只要两个相邻节点在有限的时间内没有接收到相应的时间戳,就认为这一轮时钟信息交换失败,也就是说,包发生了丢失.

图1 一组时钟信息交换过程和互为对称量测信息) Fig.1 Aset of clock information exchange processesandare symmetrical measurement information each other)
对于时间戳交换事件仅有两种情形:交换成功或者失败[15].使用伯努利随机变量描述节点Si和节点Sj间第k次信息交换的丢包事件.如果成功,则=1;否则(见表1).假定随机变量(k ∈N) 遵守独立同分布[15],则=1)=φi,j,0)=1−φi,j,φi,j为节点Si和节点Sj间的接收概率;假定随机变量和彼此独立(l/=i且n/=j或l/=j且n/=i),则
2.1.1 问题的提出
根据附录A 的详细分析,文献[2] 利用双向信息交换机制建立的系统量测模型,结合完全解耦的节点时钟状态转移方程(1),由此得到的系统时钟状态空间模型,无法满足系统状态的能观测性.
由附录A,从现代控制理论视点,对于子系统的量测模型,不管是一对邻居节点的一组量测,还是多对邻居节点的多组量测,子系统的量测矩阵C都不可逆,即根据当前步的观测值不能马上确定系统当前步的状态,进一步得知子系统的能观测性矩阵Wo的秩不为2|N[i]|(Rank(Wo)=2|N[i]|−2),即无论多少组观测值都不能确定子系统当前步的状态,换句话说,子系统是不可观测的.
2.1.2 物理过程分析、策略、M M SE 等价变换
根据现代控制理论,通过量测值确定系统内部的状态,正确地选择合适的量测模型是保证系统能观测性的关键.为此,我们引入BMU,深入研究双向信息交换的物理过程本质,希望能够建立一个辅助的绝对时钟量测模型.
结合辅助量测模型,通过线性变换,将文献[2]的相对量测模型转换为一个具有MMSE 性能等价的解耦量测模型,从而保证系统的能观测性.参考这个等价变换过程,构造一个修改的卡尔曼滤波观测器.将其描述为下面的定理1.
定理1.考虑式(8),(10),(11)和式(15),BMU的能观测性已构建MMSE 等价性能量测的必要条件:建立方程(8)∼(16) 为系统能观测性量测模型的演化线索.在BMU 分析模型下,构造符合物理过程的辅助量测模型,通过MMSE 量测性能等价变换,建立实现子系统能观测性的量测模型,实现子系统的能观测性.
已经证明(参见定理2),通过将方程(11) 中的独立量测噪声线性转换为相关量测噪声(由文献[29,6.6 节] 信号处理实例,易获得量测“相关噪声”的理解).运用分布式卡尔曼滤波能够实施MMSE 量测.
证明.
1) 能观测性策略.BMUs 能观测性的清晰证明可以参考附录B.这一部分是方程(8)∼(16) 实现能观测性证明的精炼版本,提示我们理解关键点.
2) 能观测性的量测模型–物理过程分析.这一部分将分析双向信息状态量测的物理模型与MMSE等价线性变换.
对于时钟读数模型,可以表达为标准时间和累积时钟偏移形式

当节点Si在第k次同步周期发送时钟信息时,这里k∆τ0是参考时间,而dij是节点Si和Sj间的固定时延(且dij是对称的[2,4]),D是量测节点Sj发送应答信息的相应时间;是在节点Si和节点Sj传输过程的随机时延;是在节点Sj和节点Si传输过程的随机时延.□
注意到,由统计信号处理的建模观点,由文献[29] 中的6.6 节,文献[2] 的建模参数能够通过技术方法获得(例如,量测方程(文献[2] 中的式(17)) 的噪声量测的统计方差).而观测方程(7) 和(8) 则无法直接获得.因此,文献[2] 中的式(17) 做为建模的假设前提是合理的.
1) 辅助参考绝对量测状态是真实存在的,但不可直接获得
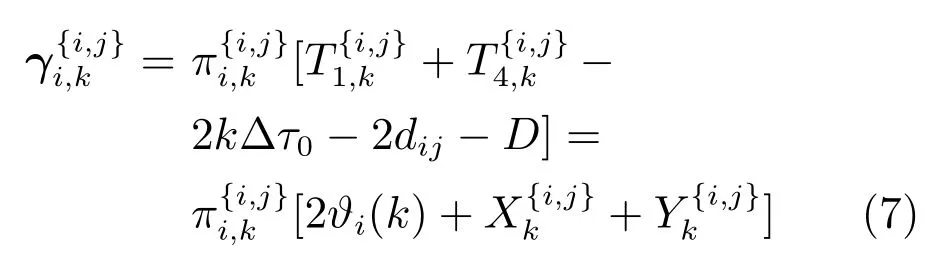
如果每一个节点Sj从节点Si处接收到发送的信息,响应立即给出,我们能够使D=0.关于节点Si邻居的所有的观测方程(7) 组集在一起,能够得到

针对节点Si的局部子系统的绝对时钟状态量测方程可表达为


式中,n ∈{1,2,···,2|N[i]|},且m ∈{1,2,···,2N}.
因为存在标准时间k∆τ0和固定时延,不能直接获得γi,k,因此,需要另一个量测模型.根据式(3)∼(6),我们能够得到节点Si的观测模型(对称量测信息可以通过另一组时间戳获得,存在于辅助量测节点中)
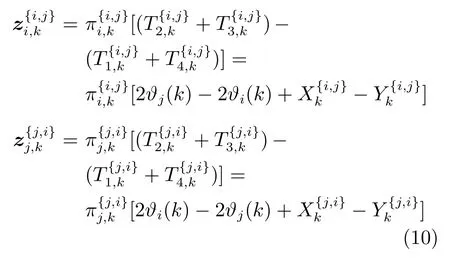
2) 双向信息交换、采集辅助相对状态量测
以节点Si为中心的所有观测方程(10) (即方程组(10)的第1 个方程) 进行组集:

式中,z i(k)=是系统的状态量测.在实际中,和对应的对称量测信息,用于更新绝对状态辅助量测,并通过辅助量测的更新消息彼此互传(参见附录B).Hi∈是量测矩阵,满足

υi(k)∈是量测噪声,符合0均值和协方差矩阵为
注意到矩阵HHHi的特殊结构,能够从观测模型(11)中提取它自身节点和所有邻居节点的状态
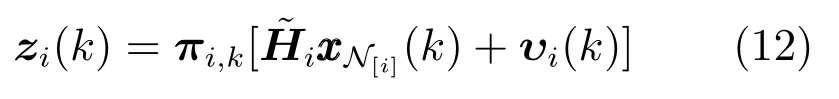
3) 组集参考绝对量和相对量的量测
对于所有Si,式(8) 和式(11)作为行交替地组集在一起,我们能够得到全局量测模型

4)局部子系统量测的 M MSE 等价线性变换

式∑中,n ∈{1,2,···,2|Ni|},m ∈{1,2,···,.Nj(o)参见注1.Pi(n,m) 直观的理解参见附录D-2中的“物理变换矩阵”.
5) 能观测性系统量测方程
在实际的大规模网络中,通过使用方程(13) 的信息交换,能够实现如方程(14) 所示的MMSE 等价变换(附录B).为了证明量测方程(11) 在辅助量测方程(8) 的协助下存在MMSE 量测性能解耦,对应于式(11),在式(14) 中抽取偶数行,我们得到一个解耦的量测方程,在MMSE 量测的等价变换上等价于能观测性方程(13)∼(15).
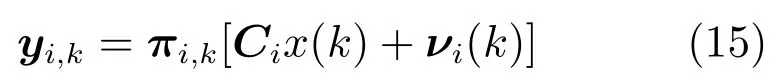
式中,y i,k=ViYYY i ∈是系统状态量测;C i=V iΓi ∈是量测矩阵,满足

νi(k)=Viψi ∈是量测噪声,符合0 均值和协方差矩阵并且V i ∈是对应于节点Si的提取矩阵,满足

注意到矩阵Ci的特殊结构,Ci中对应于其他节点的值(除了S i) 是0.因此,对于节点Si的解耦量测模型为

为了区分观测方程(11) 和(15),我们称观测方程(11) 是耦合观测方程,且观测方程(15) 是解耦观测方程.在下面的设计过程中,将解耦观测方程视为理论分析工具.
定理2.在BMU 能观测性量测模型的必要条件下,系统存在MMSE 性能等价变换.
证明.
1) 基于BMU 的MMSE 等价变换(拆分观点).
证明参见附录C.
2)多量测BMU 的MMSE 等价变换(含丢包矩阵的拆分观点).
证明参见附录D.□
2.2 含量测丢包的卡尔曼滤波
对于本文的多链路观测模型,任一节点Si共有|Ni|个邻居节点,则在对称双向信息交换时钟同步机制下的一次时钟同步信息交换中,Si共进行了|Ni|次信息交换.其中每一次信息交换都有可能会发生丢包事件,χg表示第g种丢包情况(参见表1).


使用解耦观测模型(15) 和耦合观测模型(11),能够建立解耦观测器和耦合观测器.并针对观测器量测的MMSE 性能等价变换进行了深入分析.不同于文献[2],已严格证明存在卡尔曼滤波的MMSE等价变换(参见定理2).
考虑系统的状态空间方程(1) 和解耦观测模型(16),沿着文献[9,15] 中的分析,我们组合了所有的丢包情形,并创建了修正的卡尔曼滤波:
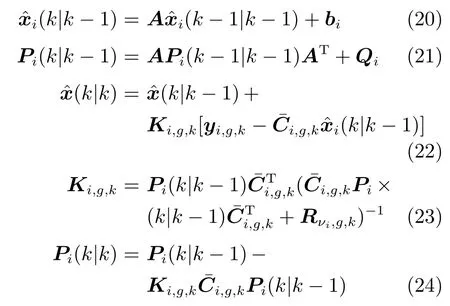
考虑系统状态方程和第3.1.2 节中耦合量测方程(12),以及辅助绝对量测方程(9),能够建立修正的分布式卡尔曼滤波.耦合量测方程(12) 仅处理它自身节点和所有邻居节点的状态.修正卡尔曼滤波的量测更新将写为下面的分布式形式

3 时钟同步长期运行稳定性统计边界
在绝对时钟建模(通过必要的基础性噪声建模,以量化时钟同步精度,方便用于大数据分析) 的基础上,能够得到基本包丢失假设模型下的时钟同步精度分析的保守边界.更多引入Markov 等包丢失模型[21],将进一步细化时钟同步精度的边界分析.
我们已经提出与模型具有MMSE 量测性能等价的解耦模型(16).子系统中心节点的MMSE 优化性能(通过邻居辅助测量节点) 与系统中其他子系统中心节点的MMSE 优化性能一致(相邻子系统有重叠).因此,本节针对本地子系统中节点的“可靠性边界”分析能够应用于全局系统中的所有节点.
卡尔曼滤波稳定性依赖于误差协方差矩阵Pi(k)=Pi(k|k−1) 收敛于某一有限矩阵.从前面的讨论,我们知道量测更新式(27) 和式(28) 在量测丢失的情形下,理论上是MMSE 性能等价的,且将式(23) 和式(26) 代入式(21)

我们知道,对于没有量测丢失的理想通信网络(πi,k=I),偶对(A,Q i) 的稳定性和偶对的可检测性能够确保Pi(k) 从任一初始条件收敛为唯一值[31].在量测丢失的情形,对于给定的初始条件P i(0),沿着时间传播的误差协方差矩阵(按时间排列的序列)是一个随机过程.考虑平均意义上的收敛,也就是,当k→∞时,E[Pi(k+1)]=E[E[Pi(k+1)|Pi(k)]]≤∞,且如文献[15] 中那样,建立相应的收敛条件和稳定域边界.如文献[15] 那样,我们以如下定理的形式给出收敛条件:
定理3 (时钟同步的收敛条件).对于给定的稳定系统(1)和(16),也就是矩阵偶对(A,Qi) 和(A,是可控和可观测的,∃0≤{φc,1,···,φc,|Ni|} ≤1,使得limk→∞E[Pi(k)]=∞,如果所有量测的接收率都在临界值,除了邻居节点j,即0≤φj≤φc,j.
根据定理3,状态估计过程的稳定性(时钟同步过程)依赖于E[Pi(k)]的收敛性,依次依赖于相对独立的邻居节点的量测的接收率.由于在多通信链路中随机的量测丢失,求解误差协方差的稳态边界非常困难.文献[15] 通过对比文献[9] 中研究的聚集量测方案,计算出收敛解的上界和下界,和对应的临界接收率的上界和下界,并且得到一个连结的k维域,这里:1) 在内域的内部,系统被定义为不稳定;2) 在外域的外部,系统被定义为稳定;3) 当处于两者之间,系统是不确定的.考虑系统(1),矩阵A的最大特征值是1,过程噪声Q i很小,产生量测的临界接收率下界=0,并且在汇聚情景下收敛解相应的下界接近于0.此外,对于时钟同步系统,应该更加关注稳定性,因此,我们焦点集中在外域的外部.
量测的临界接收率的上界能够通过以下的优化问题进行求解[15]:

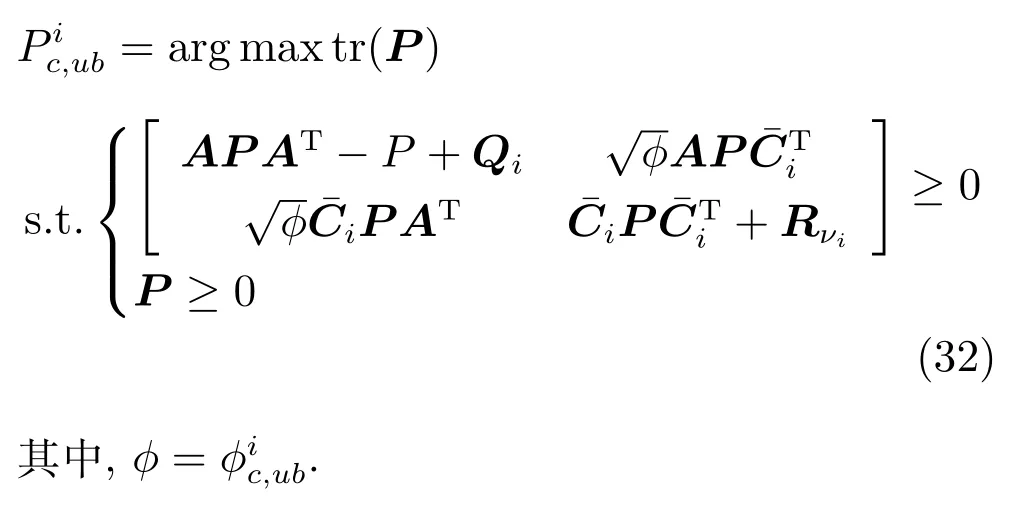
4 系统状态可靠性与性能评估
4.1 时钟状态估计精度性能对比
1) 事实上,考虑运行在独立子系统上的并行分布式滤波算法,从第4.1.1 节可知不完全能观的量测模型将导致卡尔曼滤波不稳定.
2) 由附录B 的“BMU 能观测性证明”、附录C的“MMSE 等价变换证明”,能够移除作用于文献[2] 中的式(17) 不能观量测模型下的强制“K 对角化”条件(试图解决卡尔曼滤波不稳定的状态估计).
4.1.1 问题的进一步阐释
1) 本地状态估计的必要条件
本文状态观测器设计目标之一是使观测误差e(k) 的极限趋于有限值式(33),与之等价的命题是:
命题1.若为“时钟状态追踪”(Clock state tracking) 系统,即通过引入合适的输出反馈,使“时钟状态追踪”误差系统(34) 渐近稳定(即讨论误差系统(34) 的镇定问题).
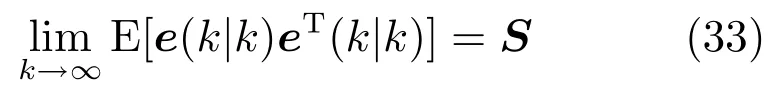
其中,e(k|k)=x(k)−对于卡尔曼滤波,使式(34) 渐近稳定,即求解合适的卡尔曼增益K使特征值|λ(A −K C)|<1.

在经典控制理论中,即是输出反馈系统的镇定问题.本文以式(38)为例,若给定一组期望的特征值{λ1(A−KC),···,λ4(A−K C)}(|λi(A−K C)|<1,则存在对应的特征方程

其中,a0,···,a3是期望特征方程对应的系数.令=A −KC,根据Cayley-Hamilton定理,有矩阵方程d()=0.

得到Ackermann 公式

d(A)是一个给定常数,若想通过式(37) 求解得到K,需保证[CA3CA2CA C]T存在Moore-Penr os e 逆.因此,[CA3CA2CA C]T一定是列满秩矩阵.对于系统(39),通过“观测器状态空间极点配置”的讨论[32−33],仍然等价于须式(39)在BMU 下式(38)能观.对于卡尔曼滤波在能观性条件下的唯一稳态解的讨论,可参考文献[34−35] (已超出本文的讨论范围.)
所以,时钟参数确定性估计的必要条件是保证系统的能观测性(参见附录B).
4.1.2 性能评估模型
1) BMU 的能观测性
a) 事实上,Si和Sj间的相对状态能够由(或测量(文献[2]中的式(17)).但和Si的状态不可观(证明见附录A),仅能确定xi(k) 和xj(k) 相对量测值.
b) 结合式(1) 与式(16),当系统在完全量测下时(不发生丢包),能够得到关于节点Si的BMU 能观测性量测模型(参见附录B)为
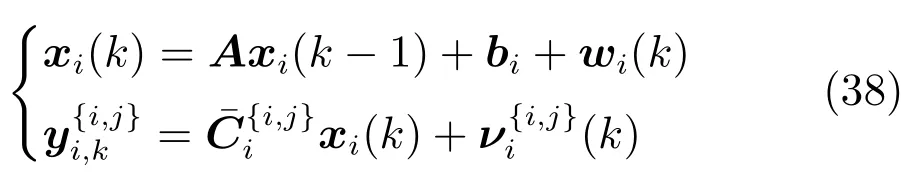
BMU 的能观测性证明详见附录B.
2) 子系统的能观测性(BMU 的线性组合)
证明详见附录B.1.性能评估请参见第4.1.3 节.
4.1.3 仿真与性能评估

定义根平方均方误差(Root average mean square error,RAMSE) 为

其中,ς ∈{β,ϑ},N是节点数量,M为试验次数.
定义根平方误差(Root mean square error,RMSE) 为
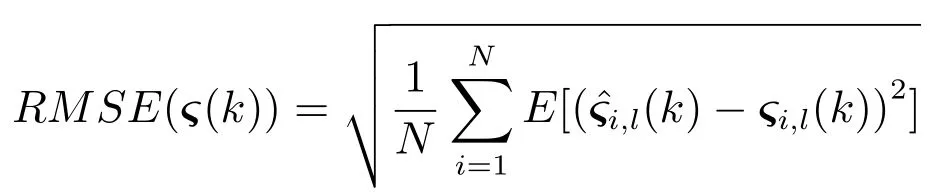
其中,ς ∈{β,ϑ}.
1) 能观测性对卡尔曼滤波的影响
参考方程(1) 与方程(12),系统的相对量测模型为

本实例BMU 的方程定义详见附录A 中式(A3).
根据附录B,我们认识到若想确定性估计可控的时钟参数,必须保证系统的能观测性.式(39) 中,在BMU 下,能观测性矩阵的秩是2,意味着式(39)是一个不完全能观测的系统(附录A).本实例比较基于式(39) 和基于式(38) 的RMSE 和RAMSE,以此评估系统的能观测性对卡尔曼滤波稳定性的影响.
由图2 和图3 可以看出,系统能观测性的缺失造成了其对应的卡尔曼滤波不稳定,即β(k) 和之间的偏差,即RAM SE(β(k)),随着步数的增加而增大.并且RM SE(β(k)) (或RM SE(ϑ(k))) 具有同样的变化趋势.而图中基于式(38) 的卡尔曼滤波则可以正常完成滤波.
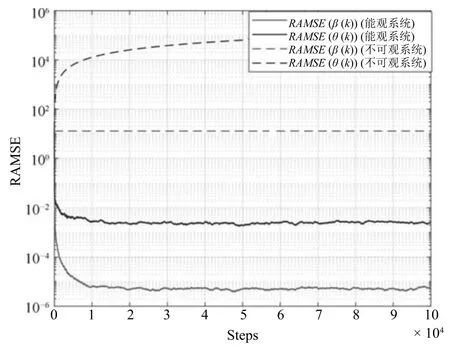
图2 可观性对BMU RAMSE 系统稳定性的影响Fig.2 Effect of observability for system stability of a BMU-RAMSE

图3 可观性对BMU-RMSE 系统稳定性的影响Fig.3 Effect of observability for system stability of a BMU-RMSE
2) 解耦量测模型的可扩展性
解耦量测模型具有MMSE 性能的可扩展性.本实例将比较不同规模的子系统的滤波性能(本质为以BMU 为单元的多量测链路子系统).根据式(38),以Si为中心,有Ni个邻居节点的子系统作如下扩展

通过观察图4 和图5,我们能够发现,随着邻居节点个数的增多,子系统在k时刻可以获得更多的量测值.卡尔曼滤波的估计性能也会因此由子系统多链路量测“过采样”而得到改善.从图中可以看出,有10 个邻居节点的子系统的RAMSE 下降最快并且也最先达到稳态.

图4 BMU 系统RAMSE 估计性能Fig.4 Estimation performance with BMU systems-RAMSE

图5 BMU 系统RMSE 估计性能Fig.5 Estimation performance with BMU systems-RMSE
4.2 不可靠工业物联网状态追踪性能评估
通过定理1、定理2 及MMSE 等价变换分析,子系统中心节点的MMSE 优化性能与其他子系统中心节点的MMSE 性能一致.不失一般性,本节中本地子系统时钟同步状态的可靠性性能评估是规模可扩展的.
在仿真中,选择4 个节点,如图6 所示.采样周期τ0=0.1s且∆=1,且=2.7×10−10.以节点S1为例,邻居节点是S2,S3和S4,相应的量测方差为:Rζ1=Rυi=diag{0.25,0.125,0.5},Rν1=diag{0.5,0.25,1}.
图6显示从每一个邻居节点的量测临界接收率与收敛的误差协方差矩阵的迹对应的上界.对于时钟同步系统中,依赖于估计的状态所需要的准确度,容易通过图6 推断出相应的网络设施质量的需求.
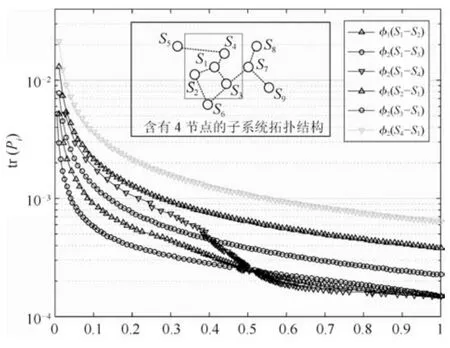
图6 测量的临界接受率— 上限Fig.6 Critical acceptance rate of measurement —upper bound
例如,要求tr(P1) 的稳态值为0.001,则对于φ1,c,ub >0.0855,φ2,c,ub >0.041,φ3,c,ub >0.2155能够定义为稳定.我们做1000次Mon t e Carlo 实验(如图7 所示).图中显示在丢包情形下(虚线) 和没有丢包的情形下(实线),迭代次数与误差协方差矩阵的迹的平均的关系,且经过验证,经过有限时间后,在统计意义下,误差协方差矩阵的迹(如图7 所示) 没有超过相应的上界.

图7 Monte Carlo 实验Fig.7 Monte Carlo experiment
针对本文的实验验证与进一步研究,相关的研究中(参见一致性算法[5,7−8]和文献[36]) 已经存在全面的阐述.对于复杂的大数据工程的适应性验证非常重要,仍需结合具体的工程实现细节进行分析.
5 结论
时钟同步系统的规划和设计中,重要的方面是同步性能的权衡.我们已经提出能观测性MMSE等价变换的状态解耦量测方程及全分布式修改卡尔曼滤波(适用于网络规模化扩展).通过理论分析时钟同步的条件和计算统计同步误差相应的上界,当前论文在时钟同步准确性与潜在的通信链路质量间已经作了量化均衡.针对规模化工业物联网的硬实时调度任务的“紧时隙”,如“工业物联网确定性调度中TDMA 紧时隙时间精度边界可靠性分析”具有重要的研究意义.
本文已经提供了包丢失假设下的可扩展研究的基本框架与线索.进一步,我们能够追踪工业无线网络Cyber-Physical 条件下状态估计的前沿研究,以全面考察规模化精确时钟同步的状态估计精度.针对时钟同步具体应用领域,本文已经提供了必需的(理论分析的)研究参考价值;进一步扩展研究的框架线索(如Markov模型[21]等);基于综合优化角度,在更全面完整包丢失信道模型假设下(如文献[28]等),则能在本文卡尔曼滤波建模基础上扩展时钟同步无线频谱感知的状态估计策略.
附录A 问题的提出
文献[2] 从一对节点出发,利用双向信息交换机制建立系统量测模型,结合完全解耦的节点的时钟状态转移方程(1),得到一个子系统的时钟状态空间模型(文献[2] 中的式(17).我们以一对节点Si和Sj(BMU) 为例,分析基本量测单元的能观测性.对于Si和Sj节点分别有下面的系统


从系统(A3) 的观测方程可以看出,第k步的观测矩阵的秩为1(x(k) 的维数为4),那么由Z(k)不能把x(k) 唯一地确定出来.考虑再加3 步观测Z(k+1),Z(k+2),Z(k+3),根据系统的观测方程和状态方程不难得出

可以很容易知道,矩阵Wo(4)秩为2,由方程(A4)知,通过Z(k),Z(k+1),Z(k+2),Z(k+3)不能把x(k) 唯一地确定出来(不存在最小二乘解),即使再增加更多的观测值,矩阵Wo(N)(N>4)的秩仍然为2,即还是不能把x(k) 唯一地确定出来(只能唯一确定偏斜和偏移的相对量(最小二乘解)).因此基本量测单元是不可观的.
对于由多组基本量测单元构成的子系统,由于基本量测单元之间的相互独立,类似一组BMU的情况,得子系统的能观测性矩阵Wo(N)(N >2|N[i]|)的秩为2|N[i]|−2((x(k) 的维数为2|N[i]|),能够唯一确定所有邻居节点Sj(j ∈Ni)与中心节点Si的相对偏移量ϑj(k)−ϑi(k) 和相对偏斜量βj(k)−βi(k).不能把x(k)唯一地确定出来(不存在最小二乘解),所以子系统是不可观的.
附录B BM U 能观测性证明
通过上述研究得知系统(A1)是不可观的,使用多组量测值仅能确定中心节点Si与邻居节点Sj之间的时钟状态相对量,为能确定Si的状态,通过分析双向信息交换机制,对每一个节点建立一个自身状态量测模型

从系统(B4) 的观测方程可以看出,第k步的观测矩阵的秩为1(x i(k) 中包含βi(k) 和ϑi(k)),那么由不能把xi(k)唯一地确定出来.考虑再加1 步的观测,根据系统(B4) 的观测方程和状态方程不难得出

B.1 由BM U 组合扩展的系统层面的能观测性证明
对于无线传感器网络(WSN)G(V,E),可以分成|E|组独立的BMU,其中|E|代表无向图G中所有边数.Si(i={1,2,···,N})为中心及其所有周围邻居节点组成的子系统,分成|Ni|组BMU,|Ni|为Si的邻居节点数.BMU(Si)={BMU(Si,Sj)|(Si,Sj)∈E,且Si,Sj∈V},其中,BMU(Si,Sj)表示由Si和Sj构成的BMU,借助辅助量测γi,k=Mixxx(k)+ζi(k),进行 MMSE 等价变换(如式(13)∼(15)所示),可以得到解耦的量测方程yi,k=+νi(k) (如式(16),不含丢包时),类似BMU的能观测证明过程,可以得到能观测性矩阵

B.2 详细的算法过程(量测消息传输、量测更新)
正是因为在实际中时钟状态的直接量测难以获得,所以有必要通过一个可用量测模型和一个时钟状态转移模型确定时钟的状态.
针对BMU,通过式(B3),我们构造出一个具有能观测性的量测方程,并利用作为时钟状态的直接量测客观存在的事实,从理论上说明(证明)MMSE 等价变换的可行性.

附录C 可靠量测下M M SE 等价变换
整个网络由多个相互独立的BMU 组成,我们以一个BMU来阐述这一过程.以BMU(Si −Sj)为例,通过双向信息交换机制,可以得到下面的量测模型

通过能观测性分析,知道在量测模型(C1) 和(C2) 下的BMU 系统是不可观的.为解决BMU 系统的不可观问题,以达到通过观测值确定系统状态,引入下面的辅助量测模型(绝对量测模型)

其中,Mi=[0 2 0 0] 和Mj=[0 0 0 2];量测噪声ζi(k)和ζj(k) 为相互独立的高斯噪声.
借助辅助量测(C3) 和(C4),对量测模型(C1)和(C2) 进行的MMSE 等价变换可以描述为

其中,令yi,k=γj,k −zi,k和Ci=M j− Hi=[0 2 00];yj,k=γi,k−zj,k和Cj=Mi−Hj=[0 0 0 2];νi(k)=ζj(k)−υi(k) 和νj(k)=ζi(k)−υj(k).方程(C5) (方程(C6))可以描述成Si(Sj) 依靠量测节点Sj(Si)达到观测自身状态.
C.1 证明过程(拆分的观点)
因为变换(C5) 和(C6) 具有对称性,只需证明其中一个即可.以Si为例,为证明式(C5)的变换过程是MMSE等价变换,我们以具有MMSE量测性能的卡尔曼滤波为观测器,证明时钟状态x i(k)在变换之前的量测模型(C1)和(C4)下的估计误差协方差矩阵与在变换之后的量测模型(C5) 下的估计误差协方差矩阵趋向一致(具有相同的收敛值).
BMU 的时钟状态转移方程为

由方程(C7) 和(C8) 组成的变换前BMU 系统在标准卡尔曼滤波下的验前估计误差协方差矩阵(State error covariance prediction)满足
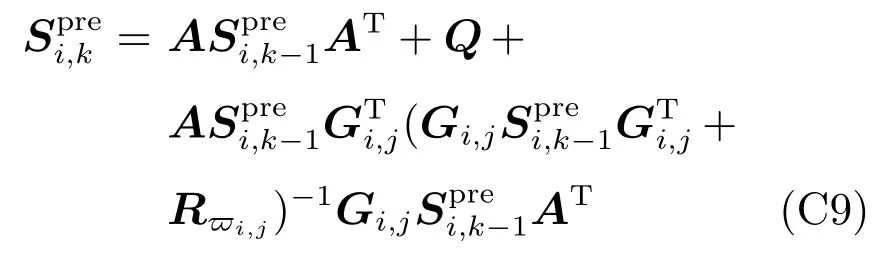
因为变换之后的量测模型(C5) 是状态解耦的,对于Sj的状态是不可观的,而为了确保BMU系统的能观测性以及不影响Si节点状态的估计误差协方差,需要(再次) 借助辅助量测(C4)(算法过程解释为需要由辅助量测输出(C4),见附录B.2),通过消息传递参与Si节点的状态估计.组合量测方程(C4)和(C5)得变换之后的量测模型为

由方程(C7)和(C1 0) 组成的变换前BMU系统在标准卡尔曼滤波下的验前估计误差协方差矩阵(State error covariance prediction) 满足

对比迭代式(C9) 和(C12),知(C9) 和(C12)有相同的收敛解(卡尔曼滤波的协方差矩阵收敛值与初始值无关,它是唯一的),甚至,当设置相同的初始值时,即,可以得到,对于∀k ∈N.所以量测方程(C10)和(C8)在 M MSE量测性能上是等价的,也显示了量测方程(C1) 在辅助量测方程(C4) 的帮助下存在MMSE 量测性能解耦.由此容易得到时钟状态xi(k)在变换之前的量测模型(C1) 和(C4)下的估计误差协方差矩阵与在变换之后的量测模型(C5) 下的估计误差协方差矩阵趋向一致(具有相同的收敛值).
附录D 多链路量测的M M SE 等价变换证明(拆分)
D.1 绝对量测与相对量测中丢包系数矩阵定义
将不可靠网络下的绝对量测方程(9) 和相对量测方程(12) 展开可表示为
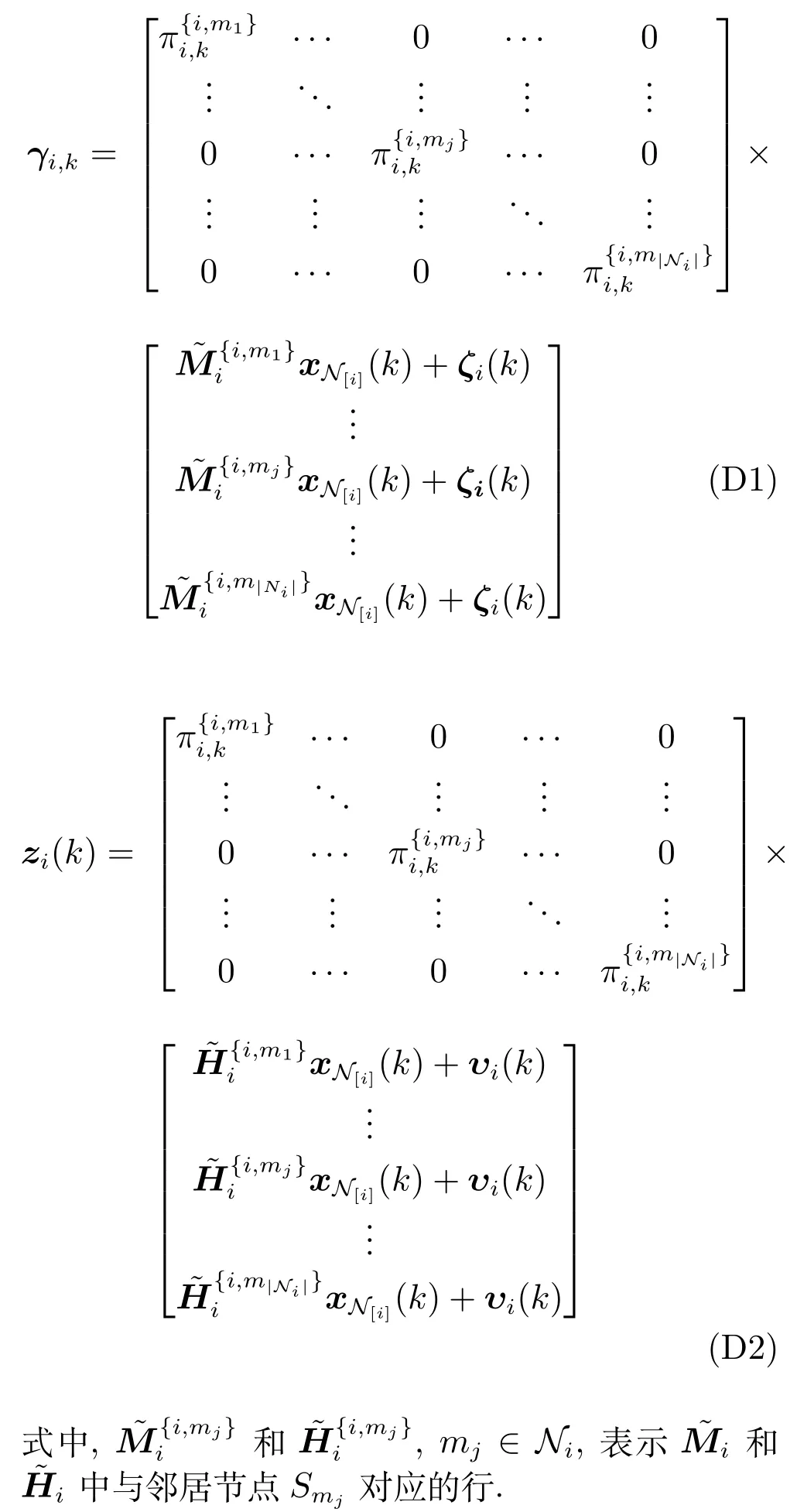
本节将以绝对量测方程和相对量测方程(D1
)和(D2) 为例,分析不可靠状态观测模型的具体表现形式.为了更清晰讨论一般情况,做以下分析:


根据丢包系数矩阵L i,g,k的定义,将式(D3) 和式(D4)重写为

D.2 多量测的M M SE 等价变换证明(拆分,可靠量测)
有|Ni|个邻居节点的Si,在不丢包情况下,系统的时钟状态方程为
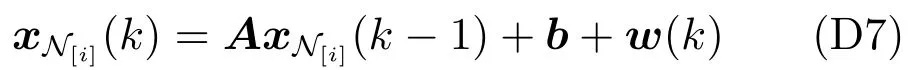
其中,状态转移矩阵A=blkdiag{ A i,A m1,···,常数项,过程噪声w(k)=[wi(k),是均值为0和协方差为Q=的高斯噪声.
1) 物理层面(PHY-level).Si相对其任意邻居节点的绝对量测方程和相对量测方程可分别表示为

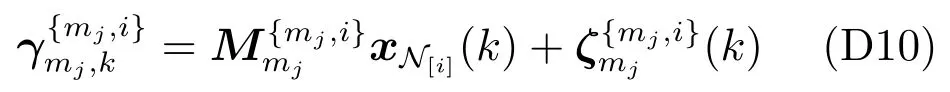
算法层面将方程(D10) 与方程(D9) 交替组合,得到以Si为中心的组合量测方程,即对应于以下形式

将方程(D11) 进行能观性变换(见附录C),可以得到新的变换后的量测方程

组合所有邻居相对Si的变换,则可分别得到式(D11) 和(D12)的组集表达式为


4) 物理变换矩阵.参考量测方程(D8),令量测模型(13)和(14)的物理变换矩阵P i=同理,则存在物理层面的MMSE等价变换(证明略).
D.3 多量测的M M SE 等价变换证明(拆分,不可靠量测)
由附录D.1 可知,在不可靠网络下,节点Si的绝对量测方程和相对量测方程可分别表示为

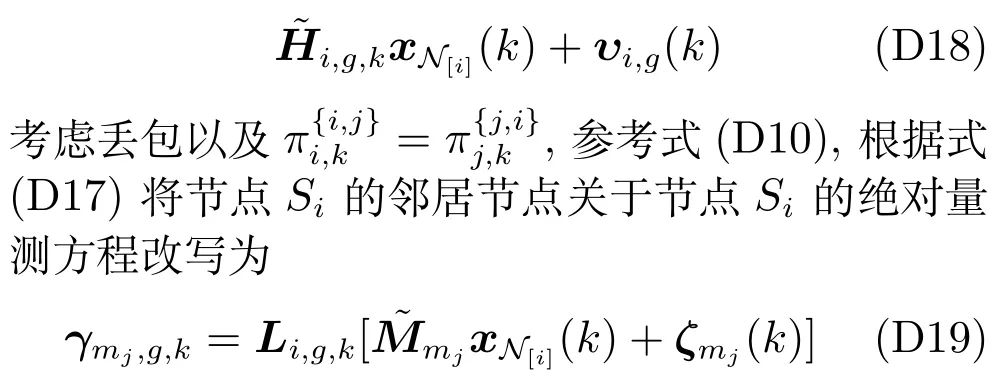
本节将在算法层面对不可靠网络下单节点多链路的MMSE 等价变换进行证明.
将式(D17) 与式(D18) 交替组合,得到不可靠网络下节点Si的组合量测模型:

将式(D19) 与式(D18) 交替组合,进行特定行变换,得到不可靠网络下变换后的节点Si的组合量测模型: