SEAs导纳控制的μ综合方法
2021-08-28李思奇黄远灿
李思奇 黄远灿
串联弹性驱动器[1](Series elastic actuators,SEAs)是一种将弹性组件串联于电机和负载之间的柔性驱动器,它具有吸收冲击,降低输出阻抗和高精度力矩输出等优点[2−5].因此被广泛应用于机器人中,以提高人机接触的安全性和舒适性,如美国Rethink Robotics 公司的Baxter 机器人[6],荷兰Twente 大学的下肢动力外骨骼LOPES[7]等各种康复/助力机器人.
为实现良好的交互行为,Hogan[8]提出阻抗控制方法.随后Colgate 等[9−10]将无源性理论用于阻抗控制的交互稳定性.Pratt 等利用前馈补偿结合PID 力控方法,提高交互性能[1].串级结构被广泛地应用于SEAs 控制,其中以力矩外环嵌速度或位置内环最流行[11−13],该结构可以实现低阻抗,但由于无源性约束,视在刚度不能超过SEAs 的物理刚度.文献[14] 设计了基于双曲正弦函数的鲁棒模糊滑模控制方法,解决柔性关节的力矩受限问题.文献[15]提出前馈补偿和模糊滑模相结合的鲁棒控制器,实现良好的位置跟踪性能和抗干扰能力.文献[16]设计基于RISE 反馈的最优控制方法,克服SEAs 的模型参数不确定和有界扰动,实现快速平稳的力矩跟踪.
H∞控制能有效地处理非结构不确定性问题[17],而µ综合方法通过不确定性结构降低了保守性[18].文献[19]针对两自由度柔性关节机器人运用µ综合方法,设计鲁棒位置运动控制器.文献[20]采用µ综合方法抑制柔性关节臂的振动问题.文献[21]在考虑参数变化和外界干扰的基础上,通过µ综合方法设计刚性并联机器人的柔顺力控制,模拟空间对接过程.
在康复机器人应用中,根据不同的康复训练模式,要求机器人能呈现大范围的阻抗变化.因此,寻找一种能任意逼近期望端口阻抗的设计方法,成为康复机器人实用化的关键.本文依据阻抗匹配的思想,利用µ综合方法设计SEAs 的导纳控制器,实现端口导纳的大范围变化.
文章的结构如下:第1 节建立SEAs 的双质量块模型,并考虑参数摄动;第2 节提出了混合交互稳定性的概念;第3 节基于µ综合方法设计了SEAs 的导纳控制器,在满足匹配精度的同时保持交互稳定性;第4 节仿真实现5 种导纳模式,验证µ综合方法设计导纳控制器的有效性;最后总结全文.
1 SEAs 建模
图1 是SEAs 的双质量块模型示意图,其中M m表示直流无刷电机的转动惯量;k表示SEAs的等效刚度;Dm表示与电机速度相关的粘性摩擦系数;Ml表示连杆的转动惯量;D l表示连杆轴承的粘性摩擦系数;τm是电机的控制力矩;τext是交互端口所受的外力.qm和q l分别表示电机侧和连杆侧的角位移.模型中忽略了弹簧的结构阻尼.
根据牛顿运动定律,列写出SEAs 的动力学方程:

式中,τs为弹簧恢复力.
图2 是描述SEAs 动力学关系的信号流图.
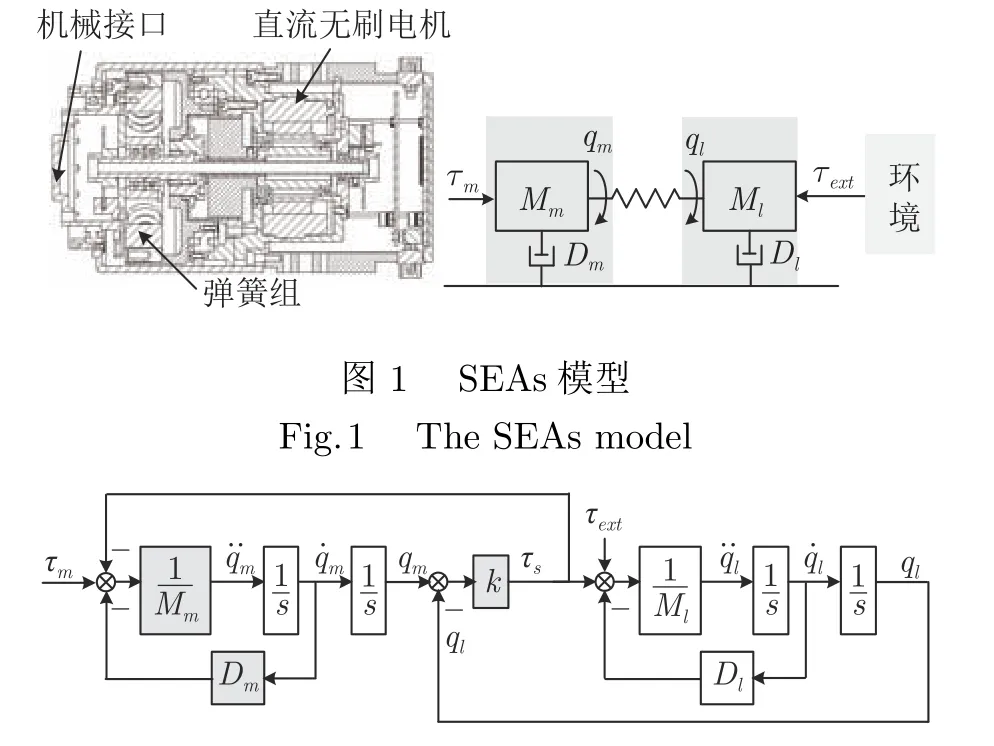
图2 SEAs 结构框图Fig.2 The block diagram of SEAs equation
在鲁棒控制中,可以将不确定性建模为外部干扰或标称模型的摄动[17].本文将摩擦中不能用与速度相关的粘性模型描述的部分,输入力矩脉动和噪声等建模为外部干扰.另外,通过等效惯量Mm、摩擦系数Dm以及等效刚度k的参数摄动描述谐波减速器和轴承等组件的不确定性[13,22].Mm、Dm和k的参数摄动分别描述如下:

式中,Mmn,Dmn和kn为相应参数的标称值;M mn,δm,D md和kd为相应参数的最大偏差值;和∆k分别表示范数小于1 的参数摄动.
下面,使用LFT 形式描述参数不确定性.首先,依据参数摄动模型,用yk,和u k,分别表示∆k,和的输入和输出,分离摄动参数.然后,将标称值部分表示为标称系统,并把参数摄动集中在一起与该标称系统反馈连接.LFT 形式的状态空间方程如下:
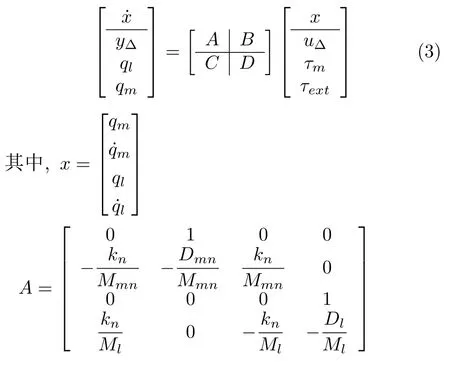
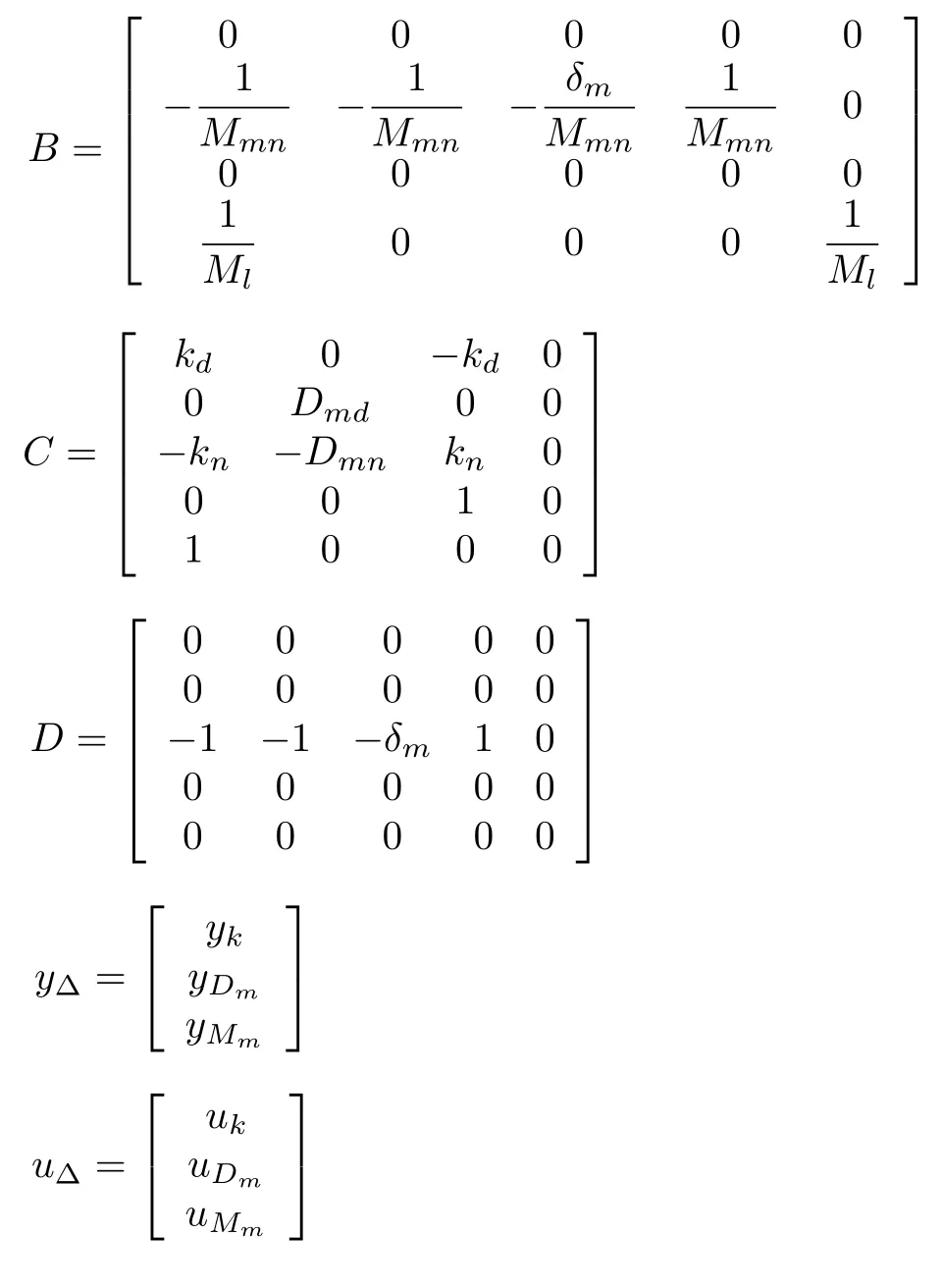
2 交互稳定性分析
无源性和小增益定理是两种常用的判断反馈互联系统输入输出稳定性的方法.小增益理论陈述的是,如果两个稳定系统增益的乘积小于1,那么这两个系统的反馈互联是稳定的[23];无源性理论表明,两个无源系统的反馈连接仍然是无源的[24].然而,高频动态经常破坏系统的无源性.文献[25]中提出基于频域的混合稳定性判据,其要求反馈互联的两个子系统,在低频段满足无源性,在高频段满足小增益定理.通过例1 阐明混合稳定性判据的基本思想.
例1.给出两个稳定单输入−输出线性时不变系统的传递函数分别为和m2,它们的Nyquist 曲线如图3 中的点画线和虚线曲线所示,其中,m1(s) 在低频段(0,1.43]rad/s 是无源的,m2(s)在低频段 (0,2.46] rad/s 是无源的.两个系统反馈互联后,在低频段(0,1.43]rad/s 维持无源性,但在高频段 (1.43,∞] rad/s 的增益乘积小于1.图3 中的实线没有围绕点 −1+j0,所以反馈互联后的系统是稳定的.

图3 混合交互稳定性实例Fig.3 An example of“mix”interaction stability
本文在使用µ综合方法设计导纳控制器时,使被控的SEAs 系统端口导纳在低频段匹配期望导纳,从而在低频段具有无源性.由于端口导纳在高频段的增益很小,因此在与人手臂环境进行交互时,通常能满足混合稳定性条件(详见图11(c)的说明).
3 导纳控制的 µ 综合
µ综合是有效的鲁棒控制器设计工具.本文采用D −K迭代算法,进行结构奇异值寻优,设计保守性较低的鲁棒控制器.
在本文中,调节变量z1W e(q l −τext Y d s−1) 衡量在设计频段上端口导纳与期望导纳的匹配精度,其实质是极小化实际位置与期望导纳依据外力给出的期望位置的差,进而实现导纳匹配.在零阻抗时,等价于接触力最小,即
图4 是考虑外部干扰和噪声后的广义被控对象,其中,P是输入到输出的传递函数;外部干扰w包括外力,nm和n l表示传感器噪声,d i为输入干扰(包含力矩脉动和摩擦等外部干扰);u是控制输入,u∆为参数摄动输入.y是传感器输出;z是调节变量,包括导纳匹配z1和控制输入限制z2;y∆是摄动输出.K即为需要设计的反馈控制器.

图4 广义对象结构简图Fig.4 Generalized plant structure diagram
图5 是带加权矩阵的导纳控制结构,其中,Y1是零阻抗时的弹簧力,Y2是位置误差.其中,Wn表示测量噪声的加权函数.本设计选择光电编码器对角度位置进行测量,其分辨率为 0.036◦,选取W n0.036;W i表示输入干扰的加权函数,该加权函数设计为一阶低通滤波器,其在 0.25 rad/s 存在一个极点[26−27],选取Wi(4s+1)−1;z2衡量控制量的大小,通过选择加权函数Wu抑制驱动器的饱和问题[19,28],选取W u(0.01s+0.1)(0.001s+1)−1.W e表示对导纳匹配精度的频率加权函数.以人臂的康复训练为例时,在小于 100 rad/s 的频段内,精确匹配导纳,选取Weζ(0.01s+1)−1,其中,δ是设计参数,根据导纳匹配精度和交互稳定性确定(详见图6).我们实现4 种导纳模型:纯弹簧,弹簧−阻尼并联,弹簧−阻尼串联和弹簧−阻尼−质量块并联.
如果只从设计导纳控制器的角度,单输出q m或q l均能实现上述控制目标.然而,文献[29]指出,当系统存在参数不确定性时,多传感器反馈能更好地鲁棒无源化.因此,本文采用qm和q l双反馈.与单反馈的比较见第4 节图10(f).
衡量导纳匹配精度的指标如下[30]:
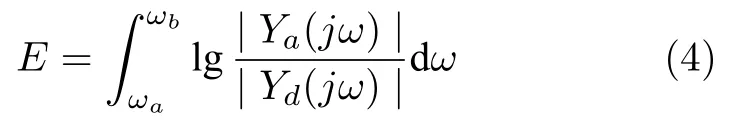
式中,Y a与Y d分别表示实际和期望的端口导纳.本文取ωa10−2rad/s 和ωb102rad/s.
图6 给出了基于导纳匹配精度并满足交互稳定性的µ综合方法.

图6 导纳控制器的求解过程Fig.6 The solving procedure of admittance controller
在零阻抗设计时,需要对照图5 修改z1,其他不变,但ζ的取值可依据实际情况调整.选择不同的初值得到不同的控制器.所以,可根据控制器阶数和匹配精度,选出合适的控制器.
4 数值仿真
依据实际的柔性关节[31−33]以及文献中人手臂的参数[30,34−35],得到如表1 所示的仿真参数.假设人手臂的反应频率f上限为 70 rad/s,即,超过该频率后,手臂的阻抗开始衰减.于是,人体手臂的阻抗模型为:
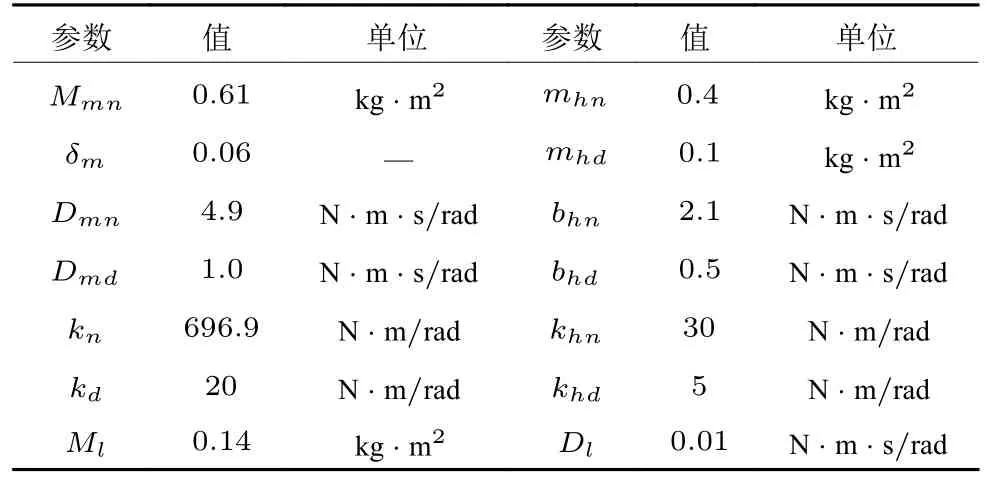
表1 SEAs 仿真参数Table 1 The SEAs simulation parameter values
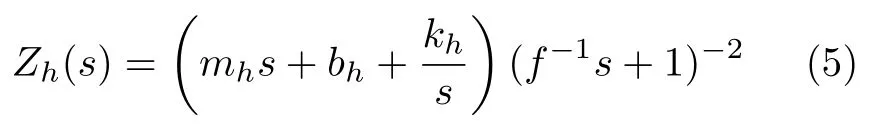
式中,m hm hn+m hd∆,b hb hn+b hd∆.k hk hn+k hd∆;m h,b h,k h分别表示人手臂质量,阻尼和刚度;mhn,bhn,khn为标称值;m hd,b hd,k hd为最大偏差值,∆ 的范数小于1.
图7 给出了理想和实际的人手臂标称阻抗模型的Nyquist 图.从图中看出,在高频段,人手臂的实际阻抗随着频率的增大而减小.
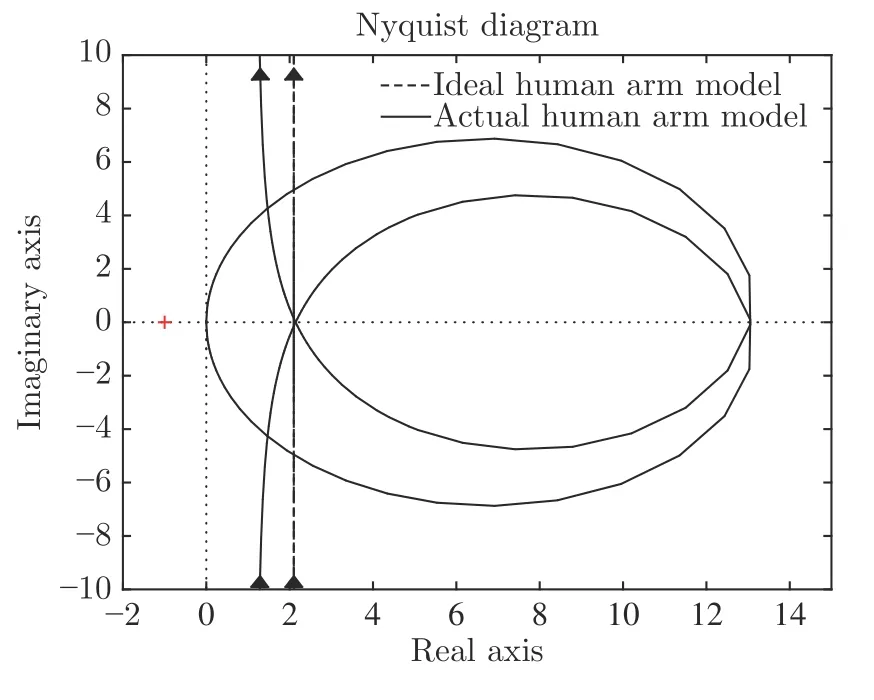
图7 人手臂阻抗图Fig.7 Impedance of human arm
图8 为控制器求解以及如何进行交互仿真验证的流程图.
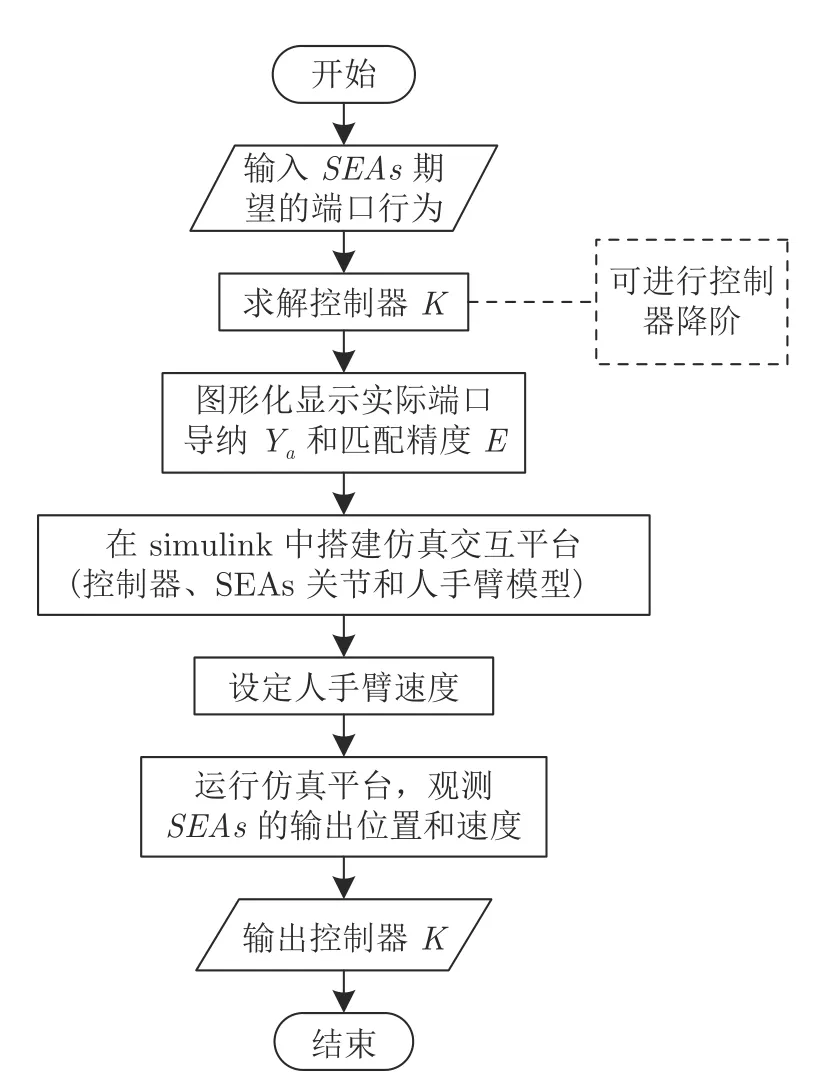
图8 控制器求解和交互仿真验证流程图Fig.8 Flow chart of controller solving and interactive simulation verification
4.1 控制器的求解
首先根据期望的端口导纳进行控制器的求解.图9 和图10(a)、(d)中虚线为含有参数不确定性的一簇实际端口阻抗/导纳频响曲线,点画线表示不控制时SEAs 标称模型端口阻抗/导纳,实线为标称模型对应的实际端口阻抗/导纳频响曲线,点线为期望的端口导纳.
1)零阻抗模式
图9 给出了满足无源性的零阻抗交互实现.从图9 中可以看到在频率小于1 rad/s(0.16 Hz)时,端口呈现很低的阻尼特性,大于该频率后,端口呈现近似Ml质量块的频率特性,端口阻抗的相角在±90◦之间,满足无源性.

图9 零阻抗的频率响应图Fig.9 Bode diagrams of zero impedance
2)4种导纳模式
图10 分别给出了4 种导纳交互模式下的端口导纳.依据混合稳定性判据,均能与人手臂进行稳定交互.
图10(a)中实现了 1000 N/m超过弹簧物理刚度的端口导纳,图10(a),(b)和(d)均能在设定的频率段实现期望导纳,但图10(c)在高频段出现了一定的匹配误差,其设计的端口导纳参数已分别在图中标注.
图10(e)给出了图10(a)、(d)中4 种形式分别与期望导纳的误差图.4 条误差曲线均随着频率的增大而增大,其中实线的误差值最小.根据式(4)计算4 条曲线在 [10−2,102] rad/s频率范围内的匹配精度值(已在图中标明),在该范围内弹簧−阻尼−质量块并联形式与期望的导纳最接近.误差曲线可准确地表征在设计期望的端口导纳过程中,不同的设计方法对应的实际端口导纳匹配情况,匹配精度值能全局衡量频段内与期望导纳的接近程度.
图10(f)给出弹簧−阻尼−质量块并联情况下(期望的端口参数见图10(d)所示),采用不同反馈情况下的误差曲线.从该图中可以清楚的看到双反馈控制的误差要小于单反馈控制.
3)举例说明控制器降阶及混合稳定性的应用
该节以导纳设计中的弹簧−阻尼−质量并联形式为例,对该控制器进行降阶并说明混合稳定性的应用.参数值如图10(d)所示.原控制器为9 阶,在对控制器的Hankel 奇异值进行评估,可知降为7 阶时误差最小,采用平方根平衡截断法进行降阶,降阶后的控制器如式(6)所示.

图10 4种导纳模式的交互设计Fig.10 Interactive design of four admittance modes
图11(a)为控制器降阶前后的误差曲线比较,实线为降阶前的误差曲线,虚线为降阶后的误差曲线,二者的匹配精度值相差 0.6 .同时图11(b)给出了降阶前后的端口导纳Nyquist 图比较.图11(c)表示交互的Nyquist 图,其控制器降阶前后的实际端口导纳见图11(b),人手臂模型的端口阻抗图见图7,实线为原控制器交互的Nyquist 曲线,虚线为控制器降阶的交互曲线,降阶前后,该曲线均没有围绕−1+j0 点,即控制器在与人手臂接触时稳定,因此降阶前后控制器均满足混合稳定性要求.

图11 导纳模式(弹簧−阻尼−质量块并联模型)控制器降阶前后的比较Fig.11 Demotion of the admittance mode controller(spring-damper-mass connect in parallel)
4.2 交互仿真
在Simulink 中搭建交互仿真平台,通过模拟人手臂推动SEAs 关节末端的过程,验证求解出的控制器.图12(a)中的虚线是给定的人手臂输出速度曲线,即人手臂缓慢加速在3 s 后以恒定的速度推动负载端.
1)零阻抗模式
图12 为零阻抗时的端口行为,图12(a)中实线为SEAs 负载末端即连杆的速度,在控制器使端口呈现零阻抗时,图12(a)两条曲线基本吻合,实现了SEAs 的跟随运动过程;图12(b) 中曲线为SEAs 末端连杆侧的位置曲线,随着施加外力,负载端的位置逐渐增大;图12(c)中实线为在实现期望速度过程中人手臂的施力曲线,虚线为SEAs 中弹簧的受力曲线,因SEAs 系统考虑了电机侧和接口侧的摩擦特性,故弹簧力应克服电机侧摩擦力;人臂施力应克服接口轴承的摩擦力和弹簧力,图中曲线符合运动过程的受力平衡情况,因此整个过程符合零阻抗的设计要求.

图12 零阻抗的交互仿真Fig.12 Interactive simulation of zero impedance

2)导纳模式
以导纳模式中的弹簧−阻尼−质量块并联情况为例,验证控制器降阶前后的交互过程,如图13所示.
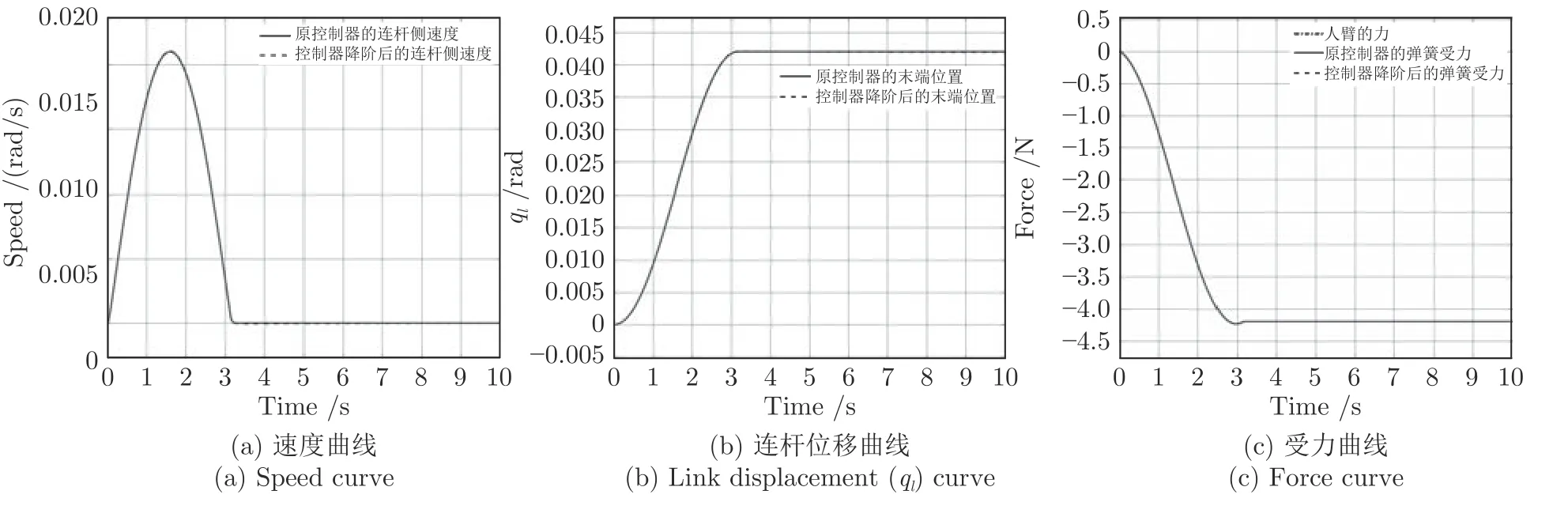
图13 导纳模式(弹簧-阻尼-质量块并联模型)的交互仿真Fig.13 Interactive simulation of admittance mode(spring-damper-mass connect in parallel)
期望的端口导纳参数如图10(d)所示,实线为原9 阶控制器,虚线为降阶后的7 阶控制器,因实际端口导纳中存在弹簧特性,SEAs 中的物理弹簧受力会与外力平衡,故负载端的位置最终会处于静止状态.对比两种曲线可知降阶前后的控制器在运动过程虽略有差别,但总体影响不大,因此控制器的求解及降阶符合设计要求.
5 总结
本文使用µ综合解决了含有不确定性SEAs 的导纳控制问题.不确定性包括模型参数摄动,传感器噪声,输入干扰和控制输入限制等.通过选择z1加权函数使受控系统的端口导纳逼近期望导纳,呈现低频段无源,高频段小增益的特点,解决了系统与环境的交互稳定性问题,实现独立于环境的导纳控制器设计.以零阻抗和4 种导纳模型的端口导纳特性为例,设计满足混合稳定性条件的导纳控制器,并对控制器进行了降阶.仿真结果表明,该方法能有效地设计SEAs 鲁棒导纳控制器.
