基于一致性的分布式变结构多模型方法
2021-08-28王昱淇卢宙蔡云泽
王昱淇 卢宙 蔡云泽
机动目标跟踪(Maneuvering target tracking,MTT)是状态估计领域的重要研究方向之一,广泛应用于雷达跟踪、飞行目标监测、导航等领域.目前机动目标跟踪方法的研究主要基于卡尔曼滤波(Kalman filter,KF).卡尔曼滤波是一种基于先验模型的估计方法,要求先验模型准确,即目标运动模式已知.然而,机动目标的机动性就体现在其运动模式未知且剧烈变化,因此单模型方法难以有效解决机动目标跟踪问题.基于多模型的跟踪方法是目前机动目标跟踪的重要研究领域.以交互式多模型(Interacting multiple model,IMM)[1]为代表的多模型机动目标跟踪方法结合隐马尔科夫模型(Hidden Markov models,HMM),利用模型转移概率提高对机动目标的状态估计精度.IMM 方法采用模型集,但Li 认为实际模式空间与模型集合不一定匹配,且模型集合应适应外界条件变化,并提出变结构多模型方法(Variable structure multiple model,VSMM)[2−5].由于其良好的状态估计效果和灵活性,VSMM 方法被国内外学者广泛关注.
随着传感器、计算机和通信技术发展,多传感器信息融合逐渐成为研究热点,可分为集中式(Centralized)、分布式(Distributed)与混合式(Hierarchical)三种融合架构[6].基于一致性的分布式融合架构无需融合中心,具有通信带宽要求低、通信能量损耗低、且对复杂网络适应性强等优点,日益受到国内外学者关注.基于一致性的分布式状态估计包括多种实现形式,例如卡尔曼一致滤波(Kalman consensus filter,KCF)[7−9]、信息一致滤波(Information consensus filter,ICF)[10−11]等.
目前对一致性滤波的研究主要基于单模型方法,主要关注传感器网络内丢包[12]、时延[13]、动态网络拓扑[14]、自适应一致性滤波[15]、网络能量优化[16]以及带牵引控制[17]等问题.近年来,考虑到多模型方法比单模型方法有更好的机动目标跟踪效果,Chisci等学者结合多模型思想,提出分布式交互式多模型估计方法(Distributed interacting multiple model,DIMM)[18−20].虽然变结构交互式多模型比交互式多模型具有更好的跟踪精度,但由于VSMM 方法中模型集随时可能扩增或删减,难以直接应用于基于一致性的分布式估计方法,因此目前已发表的相关研究成果不多.
本文重点研究如何将变结构多模型方法有效地引入分布式非线性状态估计方法,具体研究内容如下:首先为了解决量测方程非线性的问题,研究了一类无迹信息滤波方法(Unscented information filter,UIF);通过对变结构多模型方法进行改进,提出基于可能模型集的期望模式扩增方法(Expected-mode augmentation based on likely model-set,EMA-LMS),进而将VSMM 应用于分布式状态估计,提出分布式变结构多模型方法(Distributed variable structure multiple model,DVSMM).仿真实验结果验证了本文提出方法的有效性.
1 问题模型
本节介绍分布式传感器网络的图论表示以及雷达和红外传感器的量测模型.
1.1 传感器网络模型
通常用图G(V,E) 对传感器网络建模.顶点集V{1,2,···,n}表示网络中的传感器节点.如果传感器节点i和j可以通信,则认为图中这两个节点之间存在边,即 (i,j)∈E.邻接矩阵A是n行n列的布尔矩阵,记A[a ij],如式1 所示:

记Ni{j:(v i,v j)∈E}为传感器节点i可以通通信的节点集,JiN i ∪{i}.如图1 所示:包含6 节点的分布式传感器网络.

图1 用无向图表示的传感器网络Fig.1 A sensor network expressed by undirected graph
该传感器网络对应的邻接矩阵如式(2)所示:

1.2 量测模型
本文研究二维平面内直接坐标系中的机动目标跟踪问题.记视线与直角坐标系x轴正方向的夹角记为方位角θ,传感器与目标的距离记为ρ.雷达可获得目标距离ρ与方位角θ量测值,而红外传感器仅获得目标方位角θ,如图2 所示.

图2 雷达和红外传感器量测模型Fig.2 Measurement model of radar and infrared
构造极坐标 (ρ,θ) 与二维平面上直角坐标描述(x,y)一一映射,如式(3)所示,方位角的范围须为θ ∈[0,2π)或θ ∈(−π,π] :
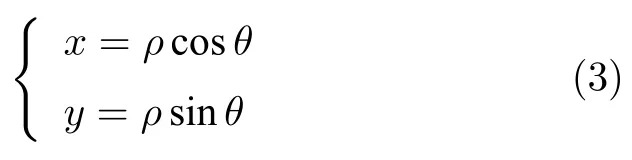
当θ ∈[0,2π)时,直角坐标 (x,y) 转换为极坐标(ρ,θ)的映射关系如式(4)所示.

式中,x t和y t表示目标位置;x s和y s表示传感器位置.式(4)中的映射关系不具有连续性,即存在一组由奇异点构成射线y0,x>0. 且目标方位角在该射线两侧发生突变,导致目标方位角误差增大,影响滤波器的状态估计结果.
为避免由反正切函数不连续引起的误差,需判断映射关系是否奇异.
首先计算相邻两个时刻目标方位角的顺时针变量∆θacw与逆时针变量 ∆θcw,构造具有连续性的映射关系,如式(5)所示,计算方位角的变化量.


图3 θ1 −θ2 的定义Fig.3 Definition ofθ1 −θ2
2 无迹信息滤波
本节介绍下一节中DVSMM 方法所采用的无迹信息滤波UIF[21]原理.无迹信息滤波与无迹卡尔曼滤波(Unscented Kalman filter,UKF)均通过Sigma 点采样计算状态向量的一阶矩与二阶矩,区别在于UIF 采用信息矩阵与信息状态向量进行量测更新.
设x为n维随机向量,其均值和协方差分别为和Px.f(·) 为非线性函数:
1)计算 2n+1个Sigma 点ξι:

式中,λ为尺度参数;表示用(n+λ)P x平方根的第i行或第i列来构造Sigma 点[22−24].
2)每个Sigma 点通过非线性函数传播,得到y i:

3)计算y的均值和协方差Py.

设离散时间非线性系统的状态方程和量测方程如式(9)所示:

式中,x k表示目标状态向量;z k表示传感器量测向量;fk(·) 和hk(·) 分别表示非线性的状态函数和量测函数;wk∼N(0,Q k) 表示过程噪声;v k∼N(0,R k)表示量测噪声.
1)一步状态预测
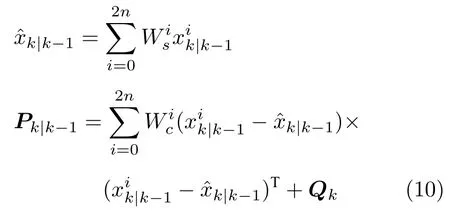

2)量测更新

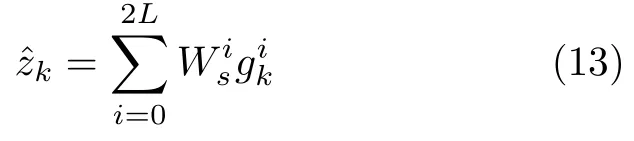
计算量测预测和状态−量测协方差矩阵:

引入伪测量矩阵计算信息状态贡献i k和对应的信息矩阵I k[21]:
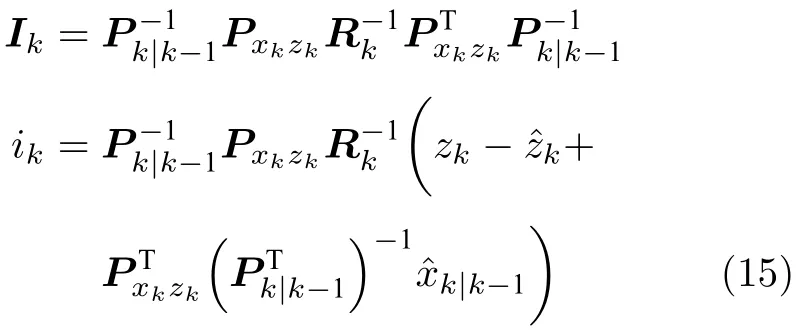
通过i k和I k计算后验信息向量和对应的信息矩阵Yk|k:
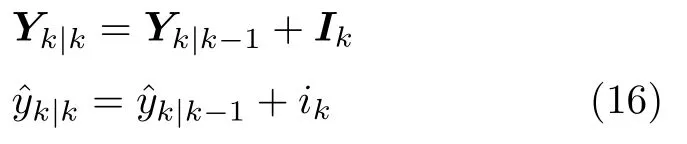

考虑到第1.2 节所述的方位角突变的问题,需要按照如下两个步骤修改UIF:

3 分布式变结构多模型方法
本节将分析变结构多模型方法应用在分布式状态估计所面临的关键问题.通过结合期望模式扩增方法和可能模型集方法,提出基于可能模型集的期望模式扩增方法EMA-LMS 与分布式变结构多模型跟踪方法DVSMM.
3.1 VSMM 方法在分布式估计的关键问题
在DIMM[18−20]方法框架下,将每个模型对应的预测信息或传感器后验估计信息与通信邻域中其他传感器对应模型中的信息进行一致性加权融合,如图4 所示:
图4 中,每个传感器具有相同的交互式多模型集,且模型数量为M.假设传感器s和j相邻,本地传感器与相邻传感器进行一致性加权融合的变量可分为三类:1)本地先验信息向量及其对应的信息矩阵Yk|k−1;2)本地信息状态贡献i k和对应的信息矩阵I k[18];3)本地后验信息向量和对应的信息矩阵Yk|k[19].此外,分布式交互式多模型方法将对每个模型下的模型似然对数与相邻传感器对应模型下的模型似然对数进行一致性加权融合[18].
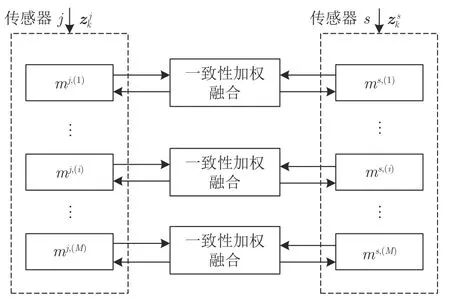
图4 交互模型预测信息的DIMM 方法示意图Fig.4 Diagram of DIMM with mode-matched PDFs
但上述DIMM 方法框架并不适用于分布式变结构交互式多模型方法.VSMM 方法中不同时刻模型集的模型种类与数量可能不同.即在每个方法周期内,每个传感器所使用的模型可能不一样.因此实现分布式VSMM 方法主要有面临两个难点:
1)信息滤波器中先验及后验的信息向量y k、对应的信息矩阵Y k和多模型方法中的模型似然都依赖于模型和传感器本地量测向量z k来计算.由于VSMM 方法每个时刻使用的模型种类和数量都在变化,因此无法像分布式IMM 方法那样对每个模型对应的这些信息使用一致性加权融合.
2)在线性系统中与非线性系统中,信息状态贡献i k和对应的信息矩阵I k的计算不但依赖于本地量测z k,也依赖于模型.
如图5 所示,每个传感器每个时刻所交互的模型不同(VSMM 方法核心特点),因此无法采用DIMM方法的思路实现分布式状态估计.

图5 分布式变结构多模型方法面临难题Fig.5 The difficulty in achieving DVSMM
3.2 分布式变结构多模型方法
由于VSMM 方法在不同时刻选用不同的模型集进行交互,因此难以在相邻传感器之间直接交互模型的信息向量和信息矩阵.为解决这一问题,本文对Li 提出的VSMM 方法结合无迹信息滤波UIF进行改进,提出分布式变结构多模型跟踪方法(DVSMM).通过在相邻传感器之间直接传递量测向量,并在每个传感器内部平行计算采用不同模型的UIF对应的信息向量、信息矩阵和模型似然函数,最后进行一致性加权融合.DVSMM 具体方法如下:
假设本地传感器为传感器s,通过MSA 方法可得k时刻本地用于状态估计的新模型集合假设每个方法周期开始时,每个传感器已经向相邻的传感器发送本时刻自身的本地量测z k和位置p k,且每个传感器可知其他传感器量测向量来自的传感器类型(雷达或红外).记JsN s ∪{s},则传感器s在本方法周期可用的传感器量测为,m ∈J s.
对模型i,目标的状态转移方程为:

传感器s的量测方程为:

假设k −1时刻基于的本地目标状态估计、状态估计误差协方差模型概率均已知.分布式变结构多模型方法的模型集合包括J s{N s ∪s}中所有传感器的量测信息m ∈J s,以及一致性加权融合过程.
在k时刻,传感器s内模型集合的一步预测和量测更新方法流程如下 (πij为模型转移概率):
1)模型交互(对∀m(i) ∈
计算模型预测概率:
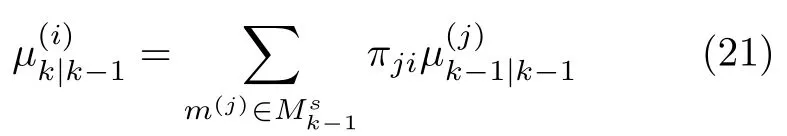
计算交互权值:

计算交互估计和方差:

2)模型条件滤波(对∀m(i) ∈
状态预测:
量测更新:

式中,Nm为传感器m的量测向量维度;|·|表示矩阵的行列式.
对模型似然求对数

至此,获得模型m(i)下,关于J s内的所有量测数据m ∈J s的信息状态贡献、对应的信息矩阵和模型似然的对数
进行一致性加权融合:

式中,w为一致性加权系数.常用的一致性加权系数有最大度加权和Metropolis 加权[25],本文采用Metropolis 加权系数.
更新每个模型下的信息向量和信息矩阵更新:
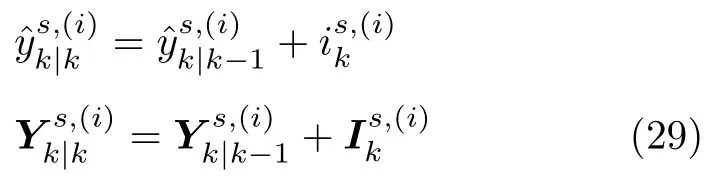
进而得到每个模型下的状态估计和状态估计协方差:

至此,DVSMM 方法具有明确的输入和输出结构与递推公式:

每个传感器通过与临近传感器交互量测信息及传感器位置,通过计算和][2],即可将各种单传感器下的VSMM 机动目标跟踪方法迁移到传感器网络中,进行分布式状态估计.
DVSMM 更新模型集方法流程如图6 所示.

图6 DVSMM 更新模型集方法流程图Fig.6 Diagram of DVSMM updating model set
3.3 基于可能模型集的期望模式扩增方法
VSMM 方法所使用的模型集合随时可能扩增和删减,其核心在于模型集自适应方法(Model-set adaptation,MSA)[3]和基于模型集序列状态估计方法(Model-set sequence conditioned estimation,MSE)[2,25].目前,模型集自适应方法包括可能模型集(Likely-model set,LMS)方法[4]、期望模式扩增(Expected-mode augmentation,EMA)方法[5]等.其中,LMS 方法根据模型概率,在一个包含较多模型的模型集中选择部分模型来参与滤波估计,能够减少每个方法周期参与滤波的模型数量,降低多模型方法的计算量.EMA 方法适用于模型具有可加性,模式空间连续的情况.它在每个方法周期对已有的模型求加权和(权值为模型概率),计算得到期望模型,并把期望模型扩增到模型集中参与滤波估计.当目标的运动模式不落在基础模型上时,能够显著改善跟踪效果.而当目标的运动模式恰好落在基础模型上时,跟踪效果相较于IMM 方法有所下降.EMA 方法取决于模型集的准确程度,若目标运动模式恰好符合模型集,EMA 方法跟踪效果.然而,考虑到实际条件下目标真实运动模式未知且难以预测,大部分情况下目标真实运动模式并不符合EMA 模型集.
针对目标真实运动模式未知且难以预测的问题,本节提出基于可能模型集的期望模式扩增方法EMA-LMS,并通过仿真分析及仿真实验结果说明分布式DVSMM 方法框架的通用性和易于实现的特点.
EMA-LMS 方法的优点在于,既能够达到EMA方法跟踪精度,又能降低每个时刻参与滤波的模型数量,即降低运算时间复杂度.本文提出的DVSMM方法通过拓展VSMM 的输入,将本地传感器的量测信息拓展为通信邻域内其他传感器的所有量测信息,并进行一致性融合估计.
EMA-LMS 方法流程如下:

3)统计与Mp毗邻(转移概率不为0)的模型集合Ma,得到本时刻需要添加的基础模型M nM a ∩.本时刻需要删除的候选基础模型M dM u −M a.
4)若Mn∅,转到第5) 步.否则计算[M n,M k−1],{得到Mn各模型状态估计值、协方差和模型概率:.然后进行期望模型的再次更新,计算估计融合 [M f,M n,E k;M k−1],由得到的模型概率计算新的期望模型.再计算一致性融合估计 [M f,M n,;M k−1],得到本算法周期的总体估计结果并令MkM f ∪M n ∪,且记Ek
4 仿真分析
本节通过仿真分析说明本文提出的DVSMM方法的有效性.考虑一个雷达和红外传感器网络,所有传感器在仿真过程中始终能观察到目标.
通过4 种方法验证本文提出的分布式VSMM框架的有效性.DIMM1 和DIMM2 分别使用了文献[18]和[19]的分布式IMM 方法框架.DIMM 3表示用本文提出的DVSMM 框架实现的分布式IMM方法.DEMA-LMS 为用本文提出的DVSMM 框架实现的分布式EMA-LMS.
假设目标为二维平面机动目标,目标的状态变量为x,x与y分别表示目标在x轴、y轴方向上的位置,与分别表示目标在x轴、y轴方向上的速度.目标状态转移方程如式(32)所示:

式中,uk[a x a y]T为目标加速度,可以进行阶跃变化;wk为过程噪声,wk∼N(0,Q k)Q k) ;Fk表示状态转移矩阵;Gk为加速度输入矩阵;Γk为噪声传递矩阵.

式中,T为采样周期;III2×2表示二阶单位矩阵;⊗表示矩阵的直积.
目标初始状态x0[0 1500 0 1500]T,过程噪声方差Qkdiag{0.01,0.01}.仿真时长为300s,T1s.目标运动加速度输入如表1 所示:

表1 目标运动模式的变化Table 1 Target mode switching
仿真中使用的基础模型集均为文献[4]中包含13 个模型的基础模型集,是具有固定加速度输入的二维CV 模型.对于模型j,目标状态转移方程为:

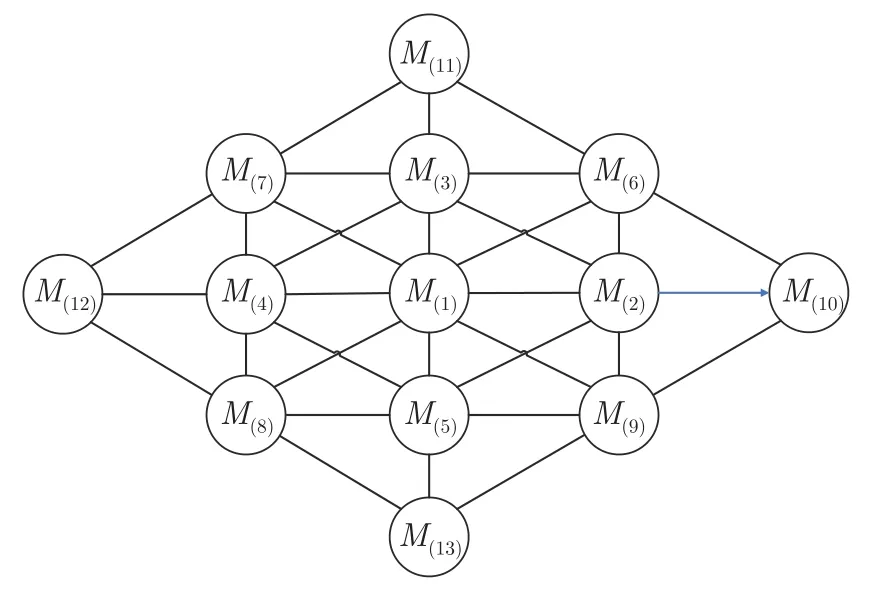
图7 模式空间内的13 个基础模型Fig.7 Basic model-set with 13 models
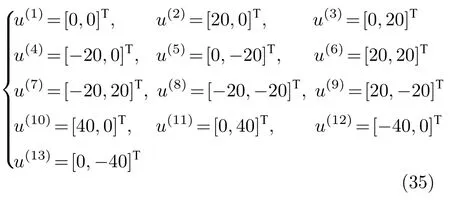

雷达传感器位置量测误差标准差为50 m,角度量测误差标准差为0.01°.红外传感器角度量测误差标准差为0.01°.雷达传感器共4 个,坐标分别为(1,0.4),(2,1.7),(3.7,1.7),(5.5,2).红外传感器共8 个,坐标分别为(2,1.2),(0.8,1.4),(3,1.4),(2.5,1),(4.1,3),(3,2),(4.5,1.8),(4,2.5).目标运动轨迹和传感器位置如图8 所示.
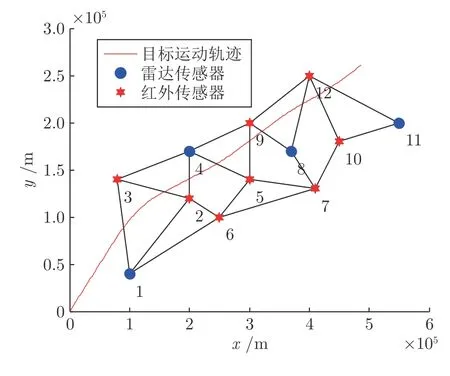
图8 目标运动轨迹与传感器类型Fig.8 Target positions and sensors types
为了比较一致性滤波的跟踪效果使用两类指标作为方法性能的衡量指标:平均位置Ep(k) 和速度估计误差Ev(k) 用来衡量传感器节点状态估计准确性;平均位置估计一致性误差Dp(k) 和平均速度估计一致性误差Dv(k) 衡量每个传感器节点状态估计的一致程度.评价指标计算见式(37)和(38).

式中,N为传感器节点数量;x与y、与分别表示状态向量中的位置和速度;和分别表示节点位置和速度估计的平均值:

进行50 次蒙特卡洛重复试验,三种方法的一致性权值都使用Metropolis 加权.仿真结果如图9~图12 所示:
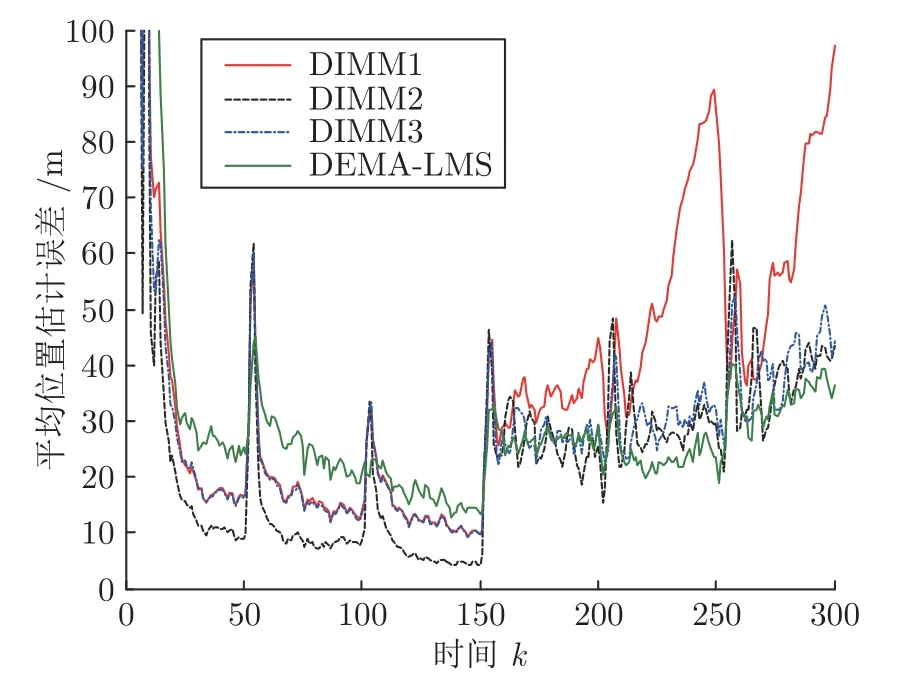
图9 平均位置估计误差Fig.9 Average position estimation error

图10 平均速度估计误差Fig.10 Average velocity estimation error

图11 平均位置估计一致性误差Fig.11 Average position estimation consensus error

图12 平均速度估计一致性误差Fig.12 Average velocity estimation consensus error
在图9~12中所示仿真实验结果中,当k <150时,目标运动模式突变前后均符合EMA 方法13 个基础模型.而当 150 1)尽管EMA-LMS 方法比较复杂,包含很多的模型扩增和删除步骤,但还是能非常方便地将其应用于分布式状态估计中,说明了本文提出的分布式VSMM 方法的有效性; 2)当目标的运动模式落在基础模型上时,通过DVSMM 实现的分布式IMM 与信息状态贡献和对应的信息矩阵一致的分布式IMM 方法效果类似; 3)当目标的运动模式落在基础模型间隙时,使用DVSMM 方法实现的分布式IMM 在运动模式位于基础模型间隙时效果比两种分布式IMM 方法更好; 4)EMA-LMS 方法运用在分布式状态估计中,效果显著,体现在当目标的运动模式落在基础模型间隙时,具有高于另外三种方法的状态估计准确性和一致性. 通过上述仿真实验结果与分析,验证了本文提出的分布式VSMM 方法的有效性.相比于分布式IMM 方法,分布式VSMM 能够根据需要灵活调整模型集结构,具备更好的适应性和状态估计效果. 本文根据一致性理论,对变结构交互式多模型方法进行改进,与无迹信息滤波相结合,提出基于一致性的分布式变结构多模型状态估计方法框架.本文方法能够在基于一致性的分布式状态估计中引入各种已有的变结构多模型方法,具有良好的跟踪精度和状态估计一致性.5 结论
