基于列生成启发式的单线电动公交车与司机整合调度优化
2021-08-28刘昊翔吴啊峰龙建成周珏
刘昊翔,吴啊峰,龙建成*,b,周珏
(合肥工业大学,a.汽车与交通工程学院;b.工业安全与应急技术安徽省重点实验室,合肥230009)
0 引言
随着我国城市化水平的不断提升和经济迅速发展,交通拥堵等城市问题随之衍生。大力发展公共交通,对缓解交通拥堵有重要意义[1]。城市公交出行研究领域中,公交车调度问题和司机排班问题一直是公交系统运营过程中的热点研究问题。如何科学、合理地安排车辆运营计划和司机排班,对城市交通资源的优化和公交企业的有效运营具有重要意义。
公交系统运营调度的优化方法主要有顺序调度模式和整合调度模式。顺序调度模式是先进行车辆调度,生成车辆运营计划,再基于车辆运用计划进行司机排班计划,顺序调度模式下进行车辆调度时,不需要考虑司机的约束。而整合调度模式下,车辆调度问题和司机排班问题相互制约,需要同时生成车辆运用计划和司机排班计划。整合调度方法是将车辆调度问题和司机排班问题作为子问题,因此,传统顺序调度问题的研究方法为整合调度问题的研究提供了重要参考。FRELING 等[2]首次提出公交车和司机整合调度问题,并给出整合调度的原因。在模型的构建方面主要有集合分割模型与网络流模型结合[2-4],优化算法方面主要有基于拉格朗日松弛的列生成启发式算法[2]、分支定价算法[3-4]等。HUISMAN 等[3]和STEINZEN 等[4]将整合调度模式分别运用于公交系统运营,并与传统的顺序调度模型进行对比,结果表明,整合调度方法能有效降低公司的运营成本。
电动公交车有零排放、噪声小等优点,为缓解交通环境污染问题,各地政府大力发展电动公交车。然而,由于电动车续驶里程短,需要充电才能完成更多的车次任务。电动公交车调度问题近年成为国内外的热点研究方向。唐春艳等[5]以最小化车辆数为目标,构建电动公交车调度模型,并设计遗传算法求解。LI[6]和杨扬等[7]设计基于列生成的方法求解电动公交车调度问题,对本文有重要的启发。司机排班问题与车辆调度问题相似,关于司机排班问题的研究非常多,一般都是构建集合分割或者集合覆盖模型,并设计基于列生成的方法进行求解[8-9]。近年来,我国在公交司机排班问题上有很多优秀的研究成果,陈明明等[10]设计禁忌搜索算法进行求解,侯彦娥[11]考虑“人车绑定”的管理模式,并设计混合元启发式算法求解司机排班问题,与“人车绑定”的模式不同,本文允许车辆和司机在多条线路之间进行联合调度,更加灵活,有利于减少司机和车辆的数量。
研究表明,传统燃油公交车与司机整合调度能有效降低公交企业的运营成本。近年来,电动公交车发展迅速,据查阅,鲜有电动公交车与司机整合调度的研究内容,故本文旨在提出电动公交车与司机整合调度问题及其求解算法。本文考虑司机连续工作时间和总工作时间约束以及电动公交车里程约束,结合现有公交车和司机整合调度模式,研究电动公交车和司机整合调度问题,并提出列生成启发式算法求解。列生成算法将问题分解为一个主问题和两个子问题,设计时空网络结合标号法求解子问题。在列生成算法得到线性松弛解后,设计深浅算法(Pure Diving)得到整数可行解,在有限时间内得到质量较高的解[12]。使用合肥市3条公交线路的基本信息生成算例,测试列生成启发式算法的有效性,并对比整合调度模式下和顺序调度模式下公交企业运营的成本变化。
1 问题描述
电动公交车和司机整合调度问题定义为:已知所有车次的信息、场站和所有终点站之间的行驶时间及距离,选择可行的司机车次链和电动公交车行车路径,使司机排班计划和电动公交车车辆运用计划覆盖所有车次,并保证司机排班计划覆盖电动公交车车辆运营计划产生的所有空驶。本文有两种空驶情况:车辆或者司机从场站出发或者回到场站;车次任务可能被覆盖多次,一次为执行任务,其余为空驶。根据公交系统实际运营情况,作如下假设:
(1)车辆从场站出发,完成1 d工作之后回到场站,驾驶车辆从场站出发的司机完成1 d 工作后没有必要一定返回场站,可由其他司机驾驶返回,保证所有车辆均回到场站。
(2)车辆从场站出发时电量是满的。车辆可以在公交线路终点站充电,假设充电时间固定,且每次都充满。
(3)为简化问题复杂度,将用餐时间考虑在司机休息时间内,司机连续工作4 h,必须休息0.5 h以上,1 d总工作时间不能大于8 h。
该问题决策如何安排电动公交车的用车计划及司机排班计划,目标函数是司机和电动公交车产生的总费用最小。电动公交车的费用包括:固定费用、每公里行驶费用、每次充电费用。本文假设充电时间固定,故每次充电成本相同,即充电成本与充电次数成正比。司机的费用由司机出勤的固定费用和司机工作单位时间产生的费用组成。需要考虑的约束包括:电动公交车里程、司机总工作时间和连续工作时间。
2 时空网络和数学模型
2.1 时空网络的构建
KLIEWER等[13]首次将时空网络应用于公交车调度问题,本文构建时空网络求解子问题,用于生成可行的司机车次链和电动公交车行车路径。
(1)车次弧
已知每个车次i∈I的起点站点li,其中,I为车次集合,终点站点,开始时间si,结束时间ei,为车次i起点站点li对应的虚拟出发节点,为车次i终点站点对应的虚拟到达节点。车次i对应的车次弧的起点为,终点为,对应的时刻分别为si和ei。
(2)出场弧
假设司机和车辆可以在任何时刻从场站出发。出场弧对应的起点是虚拟起点,终点是虚拟出发节点。
(3)入场弧
假设司机和车辆可以在任何时刻回到场站。入场弧对应的起点是车次弧的终点,终点是虚拟终点。
(4)充电弧
ε为车辆每次充电时间,假设充电时间固定,车辆可以在任意终点站s∈S充电,假设车辆在t∈T时刻在终点站s充电,则对应充电弧的起点为,终点为,对应的时间分别是t和t+ε,并且只有车辆行车路径才能覆盖充电弧。
(5)等待弧
司机和车辆可以在任意虚拟到达站点和虚拟出发站点s∈S1⋃S2等待。每条等待弧的长度为1个时间单位,假设司机在t∈T时刻在虚拟终点站s∈S1⋃S2等待,则对应等待弧的起、终点均为s,对应的时间分别为t和t+1。
(6)缓冲弧
司机和车辆完成一个车次之后需要一定的缓冲时间才能运行下个车次(司机需要休息,车辆出发之前需要检查)。设车辆运行完车次i∈I到达虚拟到达站点之后,需要进行βmin缓冲,对应缓冲弧的起点为,终点为,对应的时间分别为ei和ei+β。
为清楚了解时空网络的构建,根据表1车次信息,构建时空网络,如图1所示,节点由虚拟起点o,虚拟终点ω,两个虚拟到达站点,两个虚拟出发站点组成。
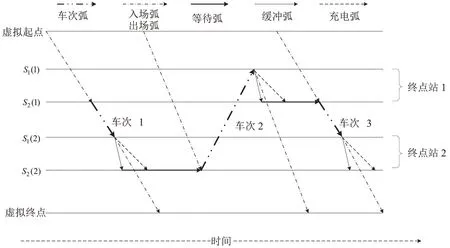
图1 时空网络生成案例Fig.1 Example of time-space network
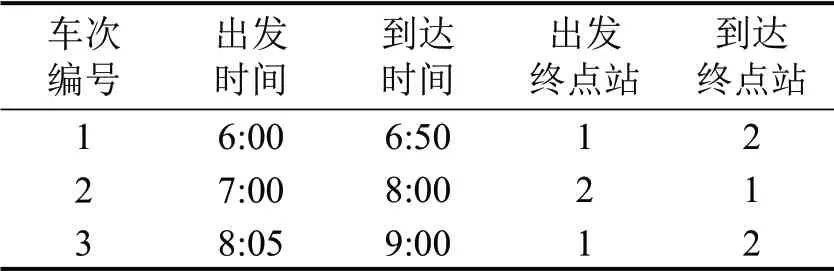
表1 车次信息Table 1 Trip information
(1)车辆可以从场站出发依次完成车次1、车次2、车次3,或者车次2、车次3。但是车辆完成车次1之后不能去运行车次3,因为车次1 的终点站和车次3 的起点站不同。车辆完成每个车次都可以在终点站进行充电或者回到场站。
(2)司机车次链的起点不一定是场站,例如司机1驾驶车辆从o出发完成车次1,由司机2继续从出发驾驶车辆依次完成车次2、车次3,然后回到d。
2.2 数学模型
列生成算法将问题分解为一个主问题和两个子问题,将复杂的电动公交车里程约束以及司机连续工作时间和总工作时间约束放到两个子问题中。主问题数学模型将公交车调度和司机排班的集合覆盖模型结合,以司机和电动公交车总成本最小为目标,在电动公交车行车路径集合和司机车次链集合中选择车辆运营计划和司机排班计划,保证司机和电动公交车运用计划覆盖所有车次弧,并且保证司机排班计划覆盖电动公交车辆运营计划产生的空驶弧。两个子问题分别生成从虚拟起点o到虚拟终点d的可行电动公交车行车路径和可行司机车次链,是资源约束最短路问题。本文主问题模型使用的变量及集合符号如表2所示。

表2 变量及符号定义Table 2 Definition of variables and symbols
电动公交车和司机整合调度问题描述为整数线性规划问题,即

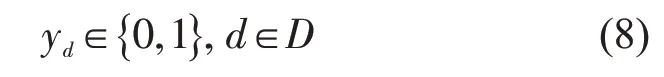
式(1)为最小化电动公交车和司机的总运营成本。式(2)和式(3)分别表示电动公交车车辆运用计划和司机排班计划覆盖所有车次弧,允许车次被覆盖多次,一次为执行任务,其余视为空驶,本文假设车次的成本固定,未考虑车次作为空驶时对系统总成本产生的影响。如果车次任务允许被车次链覆盖多次,如图2所示,矩形框表示车次,圆表示场站,虚线表示出入场或者等待,车次5 被覆盖2 次,需要两个车次链将所有车次覆盖。如果车次任务不允许被车次链覆盖多次,如图3所示,所有车次只允许被覆盖一次,需要3条车次链才能将所有车次任务覆盖。
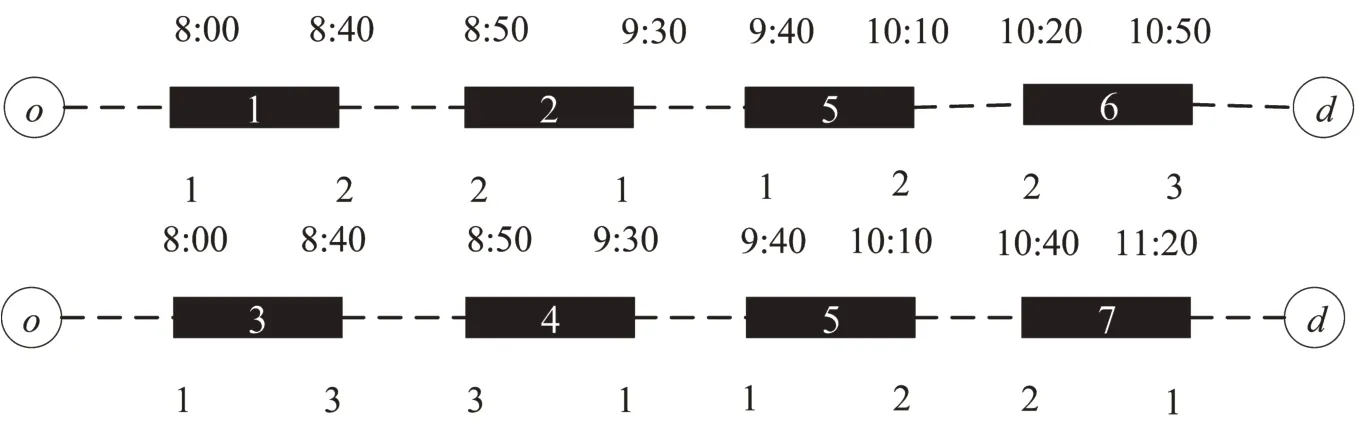
图2 车次允许被覆盖多次Fig.2 Trips that allowed to be covered multiple times
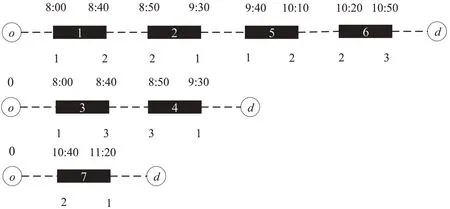
图3 车次不允许被覆盖多次Fig.3 Trips that not allowed to be covered multiple times
由式(4)~式(6)可知,整合调度模式下电动公交车车辆运用计划和司机排班计划相互影响、相互制约,需要保证车辆运用计划覆盖的车次被司机排班计划覆盖,同时,保证车辆运用计划覆盖的空驶被司机排班计划覆盖。
3 列生成启发式求解算法
3.1 列生成算法
列生成算法将问题分为两部分。第1 部分是求解限制线性主问题,对式(7)和式(8)进行线性松弛,构成限制线性主问题模型,运用Cplex求解器得到线性松弛问题最优解,设P′和D′分别为当前电动公交车行车路径集合和司机车次链集合。


第2部分是求解定价子问题,生成当前最优的电动公交车行车路径p和司机车次链d,分别加入P′和D′,继续求解限制线性松弛主问题。如果电动公交车行车路径及司机车次链的检验数大于等于零,则列生成算法终止,输出线性松弛问题最优解。
3.1.1 定价子问题
限制线性主问题对偶问题的数学规划模型为

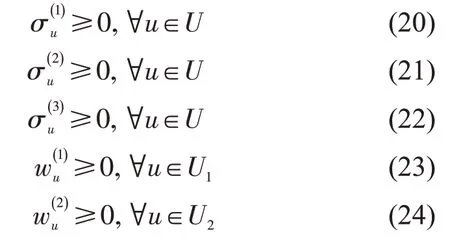
电动公交车行车路径p的检验数ξp和司机车次链d的检验数为

子问题是两个资源约束最短路问题,分别生成从虚拟起点o到虚拟终点d的可行电动公交车行车路径和可行司机车次链。对于电动公交车行车路径,主要考虑电动公交车里程约束,本文假设电动公交车从虚拟起点出发时是满电状态,可以在公交线路终点站充电,每次充电都充满。对于司机车次链,主要考虑司机连续工作时间和总工作时间约束,本文假设司机只能在公交线路终点站或者场站休息,如果休息时间满30 min,连续工作时间归零,且休息时间不计入总工作时间。
标号法在求解资源约束最短路问题具有广泛应用[14]。考虑到电动公交车里程约束和可充电的性质,设计相应的标签策略,为生成车辆行车路径时空网络中节点v∈V的标签,g为车辆从场站o行驶到节点v的累计行驶距离,设为车辆从场站o行驶到节点v的累计成本。假设标签向外拓展到,如果节点v1和节点v2对应的弧是充电弧,则g2=0,否则,为节点v1到v2之间的距离),如果g2>γ,该标签不可行,将该标签删除,其中γ表示车辆的里程约束。假设标签和标签都是节点v3对应的标签,如果满足,且,表示标签被支配,则将标签从v3对应的标签集合中删除,否则,将两个标签都加入v3对应的标签集合中。最后,在终点d对应的标签集合中选择累计成本最小的标签,回溯找到最短路径。标号法求解电动公交车资源约束最短路子问题的步骤如下。
Step 1 初始化。
Step 1.1 将时空网络中所有节点进行拓扑排序。
Step 1.4 给虚拟起点添加标签。Δot=,其中,p记录前接节点及前接标签的信息,起点o没有前接节点,所以为。
Step 2 向后接节点拓展。
从时空网络拓扑排序第1 个节点开始向后接节点拓展,并根据支配规则判断拓展后的标签是否被支配。如果该标签被支配或者不可行,则将该标签删除。
Step 3 回溯找到最短路径。
Step 3.1 在虚拟终点d的标签集合中找到成本c最小的标签。遍历所有中的标签,找到所有累计成本最小的标签。
Step 3.2 根据前接标签信息找到最短路径。如果前接标签是虚拟起点o的标签,记录最短路径,算法结束,生成可行的电动公交车行车路径。
生成可行司机车次链时,求解步骤与生成电动公交车行车路径相似,但是在设计标签时需要同时考虑司机的连续工作时间和总工作时间,设为生成司机车次链时时空网络中节点v∈V的标签,其中,t为司机连续工作时间,t′为司机从开始工作到节点v总工作时间,为司机从开始工作到节点v的累计成本。司机在完成一个车次之后开始记录其休息时间,如果休息时间大于等于30 min则司机的连续工作时间清零,休息时间不算司机的总工作时间;如果司机的连续工作时间大于α1(α1表示司机的连续工作时间约束)或者总工作时间大于α2(α2表示司机的总工作时间约束),则表示该标签不可行,将该标签删除。假设标签和都是节点v1对应的标签,如果满足且,则表示标签被支配,将标签从v1对应的标签集合中删除,否则,将两个标签都加入v1对应的标签集合中。
培育社区文化阵地。完善社区文化设施。普遍建立综合文化服务中心,打通公共文化服务“最后一公里”。市级“文化指导员”队伍深入社区帮助指导开展群众文化活动,辅导、带动基层文艺骨干和团队,提高社区文化创作、展演水平。丰富社区文化活动。立足根植群众的主体定位和雅俗共享的艺术定位,借助“靖江文艺节”“骥江大舞台”“马洲大舞台”“靖江大明星”等平台,多侧面、全方位、大视角地开展社区文化活动。擦亮社区文化品牌。结合各自地理位置、历史渊源、人文底蕴,积极打造社区文化品牌,使具有鲜明社区特色的文化活动、精品节目成为社区的名片,真正使社区文化成为居民交流沟通的桥梁、社会稳定和谐的基石。
3.1.2 列生成算法流程
在开始列生成算法之前,需要加入初始变量xp(p∈P′)、yd(d∈D′),构建初始限制线性松弛主问题模型,保证电动公交车运用计划和司机排班计划覆盖所有车次,并且保证司机排班计划覆盖所有电动公交车运用计划产生的空驶弧。在初始解生成及定价子问题的求解中,都应用标号法,并生成同时满足司机连续工作时间、总工作时间及车辆里程约束的车次链。将生成的车次链分别加入车辆行车路径集合和司机车次链集合中,同时,将生成车次链中的所有车次在时空网络中对应车次弧的成本设为无穷大。然后,继续使用标号法生成同时满足司机连续工作、总工作时间及车辆里程约束的车次链,直到所有车次都被初始车辆行车路径和司机车次链覆盖。标号法生成初始解的思想与标号法生成车辆行车路径相似,操作步骤如下。
Step 2 标号法求解资源约束最短路问题。生成一条同时满足车辆里程约束、司机连续工作时间约束、总工作时间约束车次链。将车次链分别加入车辆行车路径集合P′以及司机车次链集合D′中。
Step 3 更新时空网络车次弧的成本。将Step 2中标号法得到的车次链在时空网络对应车次弧的成本设为无穷大。
Step 4 终止条件。如果时空网络中所有车次弧的成本都为无穷大,则算法终止,输出初始车辆行车路径集合P′以及初始司机排班集合D′;否则,转到Step 2继续求解资源约束最短路问题。
生成的车辆行车路径集合P′和司机车次链集合D′作为初始可行解构建初始限制线性主问题模型。列生成算法的主要流程如下。
Step 1 构建初始限制线性主问题模型。采用贪婪算法得到初始行车路径集合P和司机车次链集合D,构建初始线性限制主问题。
Step 2 求解限制线性主问题。使用Cplex求解限制线性主问题。得到对偶变量,。
Step 3 求解定价子问题。
Step 3.1 子问题1,生成电动公交车行车路径p。更新车次弧u∈U的成本,更新出场弧u∈U1的成本,更新入场弧u∈U2的成本。使用标号法生成电动公交车行车路径p。
Step 3.2 子问题2,生成司机车次链d。更新车次弧u∈U的成本,更新出场弧的成本,更新入场弧的成本,使用标号法生成司机车次链d。
Step 4 列生成终止条件。如果电动公交车路径p的检验数ξp以及司机车次链d的检验数都大于等于零,算法迭代终止;否则,P=P⋃p,D=D⋃d,转到Step 3。
两个子问题分别用于生成电动公交车行车路径和司机车次链,将生成的车辆行车路径和司机车次链分别加入车辆行车路径集合和司机车次链集合中,由限制线性主问题模型可以看出,在求解限制线性主问题时,两个子问题相互影响、相互制约。最后,同时输出电动公交车线性松弛最优解及司机排班线性松弛最优解。
3.2 列生成启发式求解算法
SADYKOV 等[12]研究精确算法和启发式策略的结合,提出深浅算法(Pure Diving)。深浅算法是运用深度优先搜索策略处理线性松弛主问题最优解的启发式策略。本文在列生成算法得到线性松弛最优解之后,每次选择1 个小数解xp或者yd固定为1(每次选择小数解1 的差的绝对值最小),然后,使用列生成算法继续求解线性松弛主问题,直到所有的解都为整数,算法结束。基于列生成启发式的电动公交车与司机整合调度问题求解过程如下。
Step 1 初始化。设P=∅,D=∅,小数变量的集合F=∅。
贪婪算法生成初始电动公交车行车路径P和司机车次链集合D,保证所有车次被司机和电动公交车覆盖。设。
Step 2 深浅算法。
Step 2.1 列生成算法,求解线性松弛问题。
Step 2.2 终止条件。如果小数变量集合F=∅,转到Step 4;如果线性松弛主问题不可行,算法终止。
Step 2.3 更新小数变量的上、下界。选择最接近1的小数变量fc∈F,令fc=1。
Step 2.4 递归深浅算法。
4 算例与效果分析
将合肥3 条公交线路的基本信息随机生成车次数据,测试列生成启发式算法的有效性,并对比顺序调度和整合调度两种调度模式的求解结果。所有算例在配置Intel Core i7-9700k 3.20 GHz 处理器和16 GB 内存的计算机上运行,使用Visual Studio C#编译列生成启发式算法程序,涉及的线性规划问题借助数学规划求解软件CPLEX 12.6。
4.1 算例设置
3 条线路行驶距离,上、下行线路运营时间如表3所示。
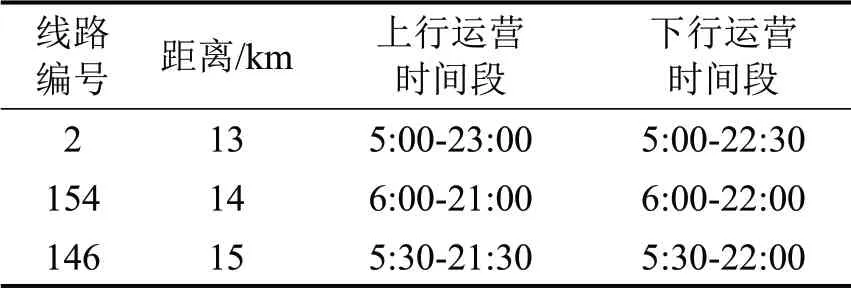
表3 3条公交车线路运营情况Table 3 Information of three bus lines
本文假设每条线路高峰时间段发出车次的运营时间相同,平峰时间段发出车次的运营时间相同。不同线路在不同时间段发车车次的运营时间如表4所示,场站距离各线路终点站的距离及时间如表5所示,其余参数如表6所示。

表4 不同时间段、不同线路车次的单程运行时间及发车间隔Table 4 One-way time,departure time interval of different lines in different time periods

表5 场站到每条线路终点站的距离及时间Table 5 Distance and time from depot to terminals of each line

表6 参数设置Table 6 Parameter settings
4.2 线性松弛问题算例测试
根据合肥市1条公交线路的基本信息,随机生成146 个车次数据,并使用列生成启发式算法求解。最终,电动公交车行车路径集合中有1435 条可行行车路径,司机车次链集合中有2069 个司机车次链。求解得到的电动公交车辆运用计划中有17 条车辆行车路径,司机排班计划中有26 个司机车次链。线性松弛最优解随迭代次数的变化情况如图4所示,Cplex 求解器共求解限制线性主问题2070次。
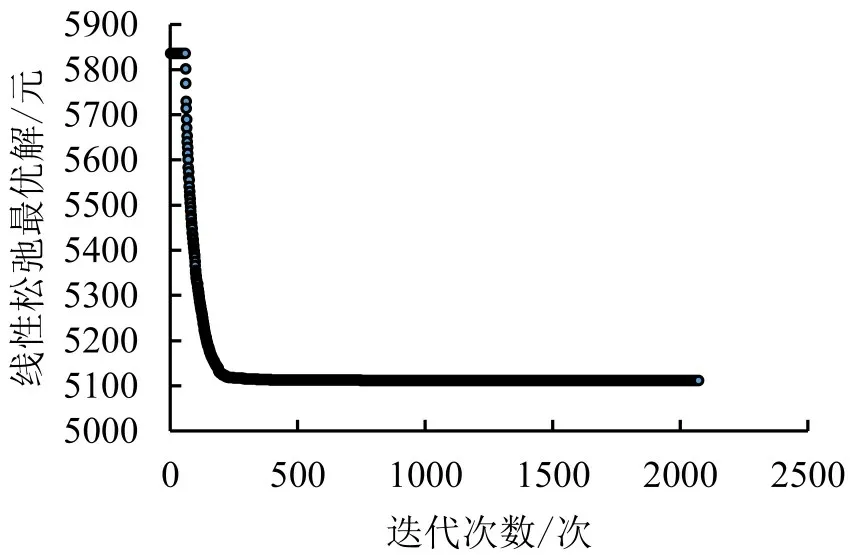
图4 线性松弛最优解在迭代过程中的收敛情况Fig.4 Convergence of optimal solution of linear relaxed problems in iterations
4.3 算法求解效果对比分析
根据3条线路的运营情况,高峰时发车间隔时间设为8~10 min,平峰时发车间隔时间设为10~15 min,随机生成3个算例,对列生成启发式算法进行测试。每个算例测试的线路编号,上、下行运营时间及每个算例的车次数量如表7所示。
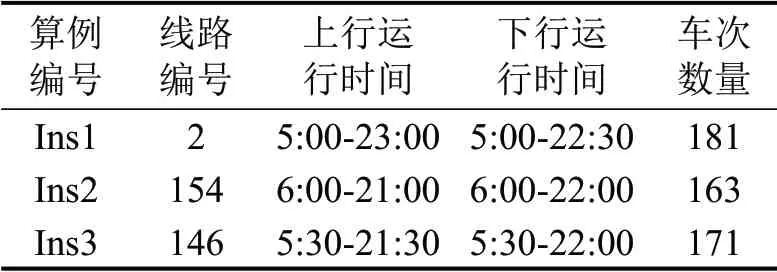
表7 算例设置Table 7 Data settings of numerical examples
表8为列生成启发式算法对3个算例的求解结果。第2 列Z是贪婪算法初始解目标函数值,第3列Zl是Cplex 求解限制线性主问题模型的线性松弛最优解目标函数值,第4列Zu是深浅算法得到整数解之后的目标函数值,第7列是求解时间,第8列表示初始可行解的生成时间,第9列表示电动公交车的充电次数,根据车辆运用计划中所有车辆行车路径覆盖充电弧的次数确定充电次数,第10 列车辆数为列生成启发式算法得到的车辆运用计划中的车辆行车路径的数量,第11 列司机数为列生成启发式算法得到的司机排班计划中的司机车次链的数量,第5 列E1和第6 列E2分别记录了最优整数解目标函数值和初始解目标函数值之间的差,以及线性松弛最优解目标函数值和最优整数解目标函数值之间的差,计算方法为

表8 整合调度测试结果Table 8 Results of integrated scheduling
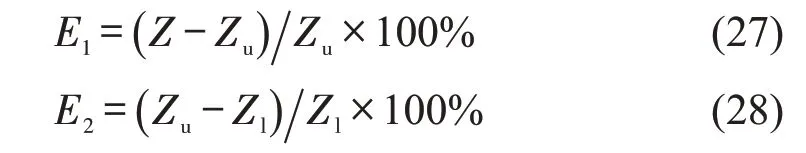
式中:Z为贪婪算法求解初始解得到的目标函数值;Zu为整合调度模式下的最优整数解的目标函数值;Zl为整合调度模式下的线性松弛解的目标函数值。
由第6列E2可知,列生成启发式算法最后的线性松弛解与最优整数解之间的差较小,说明使用深浅算法得到整数可行解的精度较高。
使用顺序调度方法测试3个算例,顺序调度方法首先使用列生成启发式方法得到车辆运用计划,保证所有车次都被车辆运用计划覆盖,然后,将车辆运用计划作为输入求解司机排班问题,保证所有车次都被司机排班计划覆盖,并保证车辆运用计划产生的空驶弧被司机排班计划覆盖。顺序调度与整合调度的对比结果如表9所示,其中,E3为整合调度目标函数和顺序调度目标函数之间的差,计算方法为

表9 整合调度与顺序调度结果对比Table 9 Comparison of results of integrated scheduling and sequential scheduling
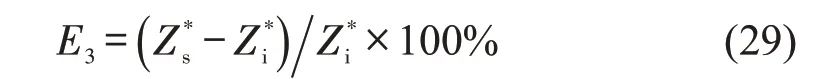
对比表9整合调度与顺序调度结果,得到如下结论:
(1)顺序调度模式下的车辆数比整合调度模式下的车辆少。由于顺序调度模式是先进行车辆调度,生成车辆运营计划,再基于车辆运营计划进行司机排班计划。因此,顺序调度模式下进行车辆调度问题研究时,只需要考虑电动公交车里程约束;整合调度模式下同时生成车辆运用计划和司机排班计划,生成车辆运用计划时需要保证车辆运用计划中的空驶被司机排班计划覆盖,导致顺序调度模式下的车辆比整合调度模式下的车辆少。
(2)整合调度模式下的司机数量和公交企业运营总成本明显比顺序调度模式下少。由于顺序调度模式是先进行车辆调度,生成车辆运营计划,再基于车辆运营计划进行司机排班计划,因此,顺序调度模式下进行司机排班时车辆运用计划中的空驶信息固定,需要保证所有车次以及车辆运用计划中的空驶被司机排班覆盖;而整合调度下车辆运用计划和司机排班集合相互制约、相互影响,会考虑车辆运用计划对司机排班计划的影响,因此,一般整合调度模式下的司机数量与公交企业运营成本都比顺序调度模式下少。
5 结论
本文研究电动公交车与司机整合调度问题,考虑电动车的里程约束和司机的连续工作时间和总工作时间约束,同时生成电动公交车车辆运用计划和司机排班计划,并保证车辆运用计划的空驶被司机排班计划覆盖,以合肥市3条公交线路的基本信息随机生成时刻表数据进行求解测试,结果表明了本文所构建的集合覆盖模型和列生成启发式算法的有效性。由E2的值可知,深浅算法在较短的时间内能够得到精度较高的整数解。整合调度和顺序调度的对比结果表明,整合调度能有效减少公交运营成本和司机数量。
