既有框架性能化抗震鉴定方法研究及工程应用
2021-08-27程绍革朱毅秀张伟平
程绍革,朱毅秀,杨 欣,孙 魁,张伟平
(1.中国建筑科学研究院有限公司抗震所,北京 100013;2.同济大学土木工程学院,上海200092;3.中国人民军事革命博物馆,北京100038)
既有建筑的性能化抗震鉴定是未来的发展方向,主要包括性能目标的确定和既有建筑所能达到的性能目标分析两方面内容。现行《建筑抗震鉴定标准》(GB 50023−2009)[1]中不同后续使用年限对应不同的既有建筑遭遇预期地震破坏程度,是性能化鉴定的体现,但过于粗糙,不能很好适应今后建筑业的发展需求。
目前国际上钢筋混凝土框架结构的抗震性能和损伤程度通常以变形作为主要性能指标,ATC40、ASCE 31−03、ASCE 41−13和FEMA 273等一系列性能化鉴定(设计)规范[2− 5]将整体结构性能状态划分多个状态,并给出了相应的变形限值。同时,也对构件的损伤状态和变形界限给出了相应的定义和限值。在性能化鉴定方面,我国建筑抗震设防目标是“小震不坏,中震可修,大震不倒”。但这一设防目标对应的潜在损伤状态缺乏量化衡量描述,震害导致停产或建筑停用造成的经济损失远远超出预期[6]。20世纪80年代,工程师开始使用最大损失概率(PLM)来衡量结构抗震性能,PLM 指超越概率为10%的震后修复费用估计[7],后期进一步颁布了ASCE 31−03、ASCE 41−13作为相关参考技术标准,近年来又发布了FEMA P−58给出了工程结构的全概率抗震性能评定方法。FEMA 237提出了与地震概率相关的多水准性能目标,该技术标准对非结构构件和结构构件的性能水准划分以及对应的变形限值给出了详细定义[8],值得借鉴。
地震易损性评估方法有3种[9−11]:震后调查、专家经验和模拟分析。实地调查存在局限性,对于评估与震害区场地条件和基础设施条件差别较大的地区内结构抗震性能,可能难以得到满意的评估结果。ATC-13报告给出了采纳专家经验意见的民用基础设施的易损性函数[11],以此来弥补圣费尔南多震害调查的数据的局限性,但因为易损性曲线是根据主观建议提出的,因此其易损性曲线的可靠度是未知的[12]。为了解决专家经验和震害调查结果的不足,最新的易损性分析采用模拟分析方法建立结构地震响应与地震强度之间的关系,包括非线性时程分析和逐步增量动力分析方法,其中逐步增量(IDA)动力分析方法逐渐成为主流方法,相比于非线性时程分析,逐步增量动力分析的计算量更大。Cornell等提出了基于结构抗震性能,适用于抗震设计和评估的概率分析理论框架,该理论体系考虑了地震风险、结构自身、结构损伤和经济损失的不确定性[13],为加州规范设计方法提供了概率理论基础。
2016年“十三五”国家重点研发计划课题“既有公共建筑防灾性能与寿命提升关键技术研究与示范”(课题编号:2016YFC0700706)启动,其中“基于使用年限和性能的抗震鉴定技术”是重点研究内容。课题组经过4年的努力,提出了不同后续用年限内的地震作用计算理论,通过震害总结与振动台模型试验,提出了既有建筑抗震性能的细划准则,在地震易损性分析方法开展了进一步的研究,建立了结构地震易损性矩阵,并引入震害指数,形成了既有建筑性能化抗震鉴定的完整方法。部分研究成果在某博物馆展览大厅的抗震加固前后的抗震性能对比分析评估中得到应用,起到了很好的示范效果,研究成果还将纳入今后《建筑抗震鉴定标准》(GB 50023−2009)[1]的修订中。
本文将基于性能的既有建筑抗震鉴定研究的主要研究成果、基本鉴定方法和流程作简要介绍,供鉴定加固工程技术人员参考。
1 既有框架结构的性能水准划分
1.1 框架结构振动台试验模型设计
选取了一栋建于20世纪70年代的办公楼按1/5缩尺比例设计了模型,原结构设计标准略低于《工业与民用建筑抗震设计规范》(TJ11-78)[14],代表了20世纪70年代在中国建造的混凝土框架结构。模型平面见图1,为考虑地震作用下填充墙的破坏情况,在模型纵向外框架的②~③、⑥~⑦柱间布置了黏土砖填充墙。
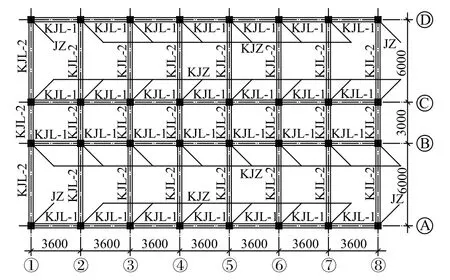
图1 试验模型结构平面布置图Fig.1 Layout of testing structure model
模型采用混凝土与镀锌铁丝制作,其中混凝土强度等级与原型结构相同(C18),模型构件配筋按楼层等屈服强度系数的原则设计[15]。完工后模型底层层高800 mm、其余层高720 mm,总高度3.88 m,其中底座高0.2 m,模型全景见图2。为满足模型动力试验的相似律要求,试验时附加配重34 t,模型总重达56 t。

图2 试验模型全景图Fig.2 Picture of the model before test
1.2 振动台模型试验方案
试验采用El-Cenro波、Taft 波和Ⅲ类场地人工波RD1,在低幅激振阶段选用3条波进行激振试验,模型主要构件开裂后选择地震响应最大的波(实际试验时选用了Taft 波)进行激振。
试验时台面激振加速度峰值逐级增大,模拟设防烈度6区~9区的三水准地震作用,使模型依次经历弹性阶段、弹塑性阶段直至濒临倒塌,每次激振完毕均进行白噪声扫频试验,记录模型自振频率、阻尼系数的变化,并观察模型受损情况。
试验以纵向激振为主,仅弹性小震阶段进行双向激振试验。
试验加载制度及测量方案详见文献[15]。模型底座和各楼层均布置了加速度传感器,采用激振过程中的各楼层的加速度反应时程,对加速度反应时程进行两次积分得到楼层的位移响应时程,通常由于一些干扰因素,微小的误差在积分过程中会被放大,失去真实性,经试验验证通过消除趋势项及滤波处理,可以得到满意的二次积分效果[16−17],本文位移时程均由振动台STEX3.0程序处理后积分计算给出。取同时刻相邻楼层位移时程曲线差的绝对最大值除以层高,求得相应楼层层间位移角。
1.3 模型破坏现象与试验数据对比[15]
1.3.1模型试验全过程动力特性的变化
图3、图4为试验全过程模型基本频率和阻尼系数的变化曲线图。从图中可以看出,模型结构的基本动力特性全过程曲线可分为4段:
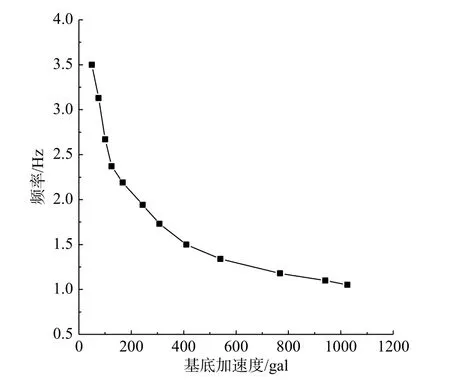
图3 试验全过程基本频率变化图Fig.3 Fundamental frequency during test produce
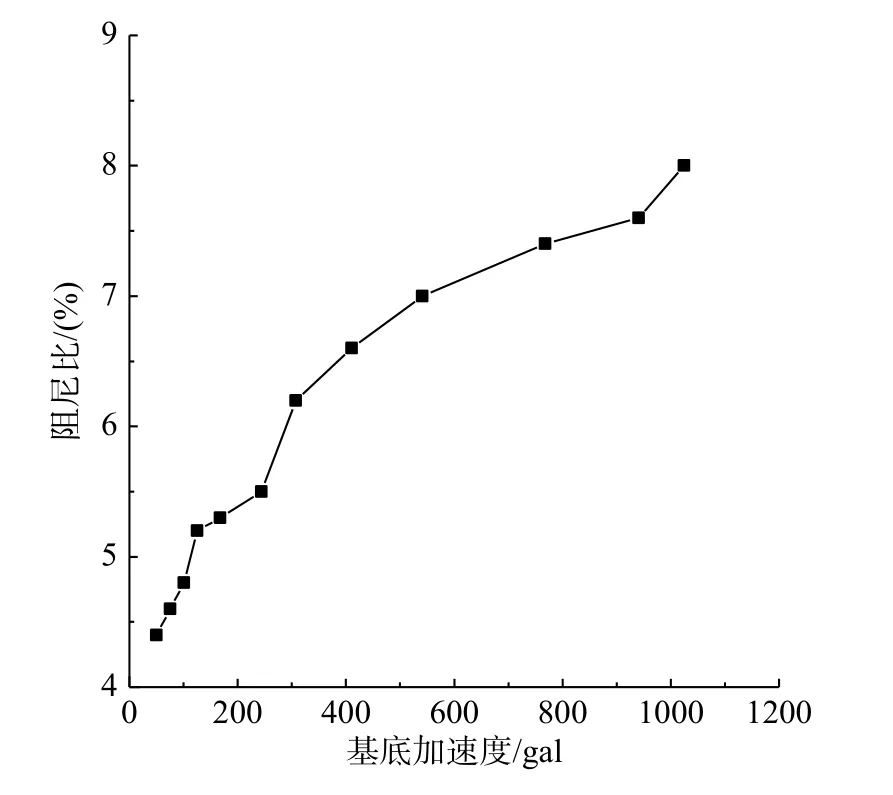
图4 试验全过程阻尼系数变化图Fig.4 Damping ratios during test produce
1)第一段为台面加速度峰值50 gal、80 gal、100 gal、150 gal 的试验阶段,该阶段的频率下降曲线较陡,阻尼系数增幅较大。
2)第二段为台面加速度峰值180 gal、200 gal、300 gal的试验阶段,该阶段的频率下降曲线与第一阶段相比略趋平缓,阻尼系数增幅也趋平缓。
3)第三段为台面加速度峰值400 gal~920 gal的试验阶段,该阶段的频率下降曲线更加平缓,阻尼系数增幅开始增幅较大,后趋于平缓。
4)第四段为台面加速度峰值1000 gal激励试验阶段,该阶段频率下降略增大,阻尼系数有较大的提高。
采用能量法对模型结构的自振周期进行了计算[13],理论分析结果表明:纵向不考虑填充墙刚度贡献时的基本周期为0.31 s,考虑填充墙刚度贡献但对其刚度进行折减后的基本周期为0.28 s。实测结果为:纵向基本周期为0.29 s,经历80 gal激振后的基本周期为0.32 s。
理论分析与实测结果对比表明,经80 gal的激振后,模型基本周期则与纯框架基本周期吻合。从试验观察到的现象来看,模型经台面加速度幅值50 gal 的白噪声扫频后,底部几层填充墙局部与主体结构有脱开现象;经80 gal 的地震波激振后底部几层填充墙基本与主体结构脱开,个别填充墙出现水平或斜向裂缝,说明填充墙的刚度贡献已完全丧失,但承载力贡献仍存在。
1.3.2 模型不同破坏阶段的最大层间位移角1)填充墙开裂
从试验观察到的现象来看,模型经台面加速度幅值50 gal 的白噪声扫频后,底部几层填充墙局部与主体结构有脱开现象。经80 gal 的地震波激振后底层几层填充墙基本与主体结构脱开,个别填充墙出现水平或斜向裂缝。由3条波激振下的层间位移角实测结果可知,最大值为El-Centro波反应最大,已接近1/700。
2)结构构件初始开裂阶段
模型在台面加速度峰值100 gal 时,最大楼层层间位移角略超规范1/550限值,个别框架柱的柱中或柱顶开始出现微细裂缝,但从模型的基底剪力-顶点位移曲线上看,模型仍处于弹性状态。当台面加速度峰值达到130 gal时,框架柱裂缝发展开始明显(见图5),此时模型最大层间位移角已达到1/410,且模型已开始进入弹塑性变形阶段。

图5 框架柱开裂Fig.5 Crack of column
3)模型弹塑性变形阶段
当台面输入加速度峰值达到300 gal 时,框架柱裂缝连通,但缝宽发展仍不大,底部3层的层间位移角达到了1/200;当台面输入加速度峰值达到540 gal时,大数框架柱出现连通裂缝,缝宽略有发展,有少量框架柱混凝土压溃、纵筋压屈,此时最大楼层位移角在1/100左右,此阶段模型的层间位移角分布见图6。
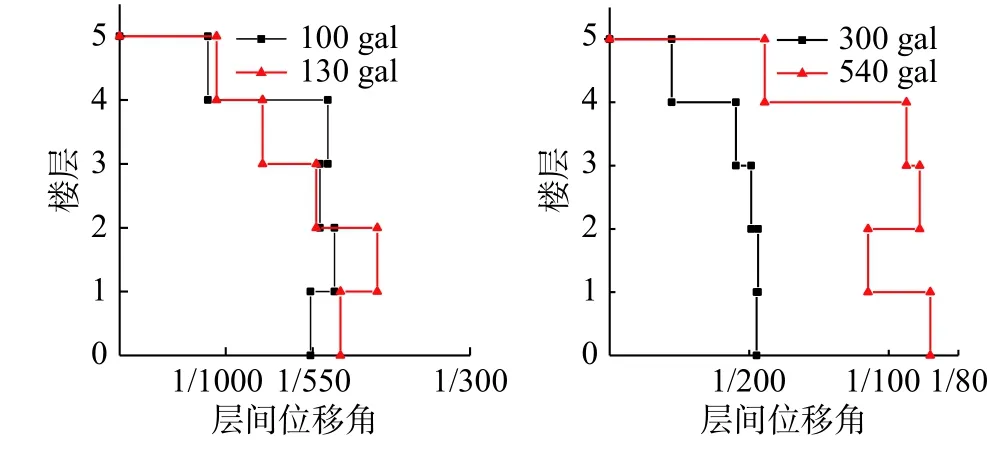
图6 楼层最大层间位移角Fig.6 Maximum inter story drift
4)模型大变形至濒临倒塌试验阶段
当台面加速度峰值达到770 gal时,3层形成明显的薄弱层,多数柱端形成塑性铰;台面加速度峰值达到940 gal 时,观察此时的结构破坏形态3层全部柱项出现塑性铰(见图7);加速度峰值1025 gal 时,框架柱两端破坏严重,柱顶部混凝土剥落,纵筋压屈呈“灯笼”状,模型产生不可恢复的侧向变形(见图8),濒临倒塌。此阶段模型的层间位移角见图9。

图7 框架柱顶全部出现塑性铰Fig.7 Plastic hinge formed in all columns

图8 模型产生不可恢复变形Fig.8 Irrecoverabledeformation of model
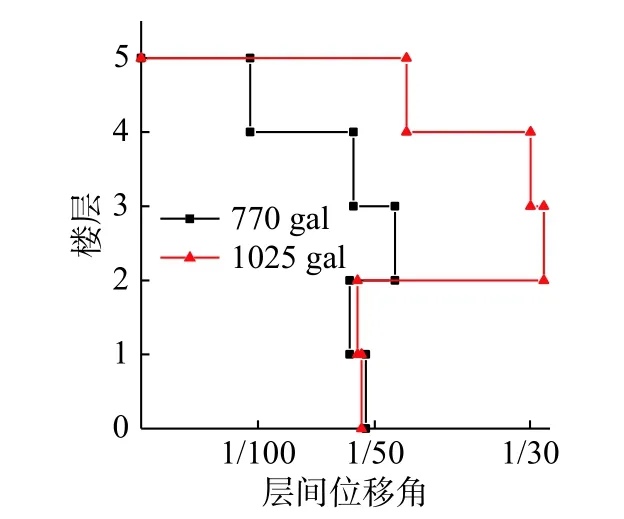
图9 楼层最大层间位移角Fig.9 Maximum inter story drift
台面加速度峰值达到770 gal 时,最大层间位移角已超规范规定的1/50限值,台面加速度峰值达到940 gal时,最大层间位移角达1/40;加速度峰值1025 gal 时,最大层间位移角超过1/30。
1.3.3 基于层间位移的结构抗震性能水准


2 地震易损性分析过程简介
2.1 分析用框架结构设计
以试验模型的原型结构为基准,分别按《工业与民用建筑抗震设计规范》(TJ 11-78)[14]、《建筑抗震设计规范》(GBJ 11-89)[23]、《建筑抗震设计规范》(GB 50011−2001)[24]、《建筑抗震设计规范》(GB 50011−2010)[21]重新进行结构设计,包括基准结构在内共设计了5个分析模型,分别代表不同历史时期的建筑,本文以下简称78版结构、89版结构、01 版结构、10版结构和原型结构。
5个分析结构之间体现了抗震验算方法、抗震构造措施、材料强度等级、内力调整系数的差别。
2.2 分析软件及建模中的特殊处理
采用ABAQUS大型有限元软件进行结构分析,楼板采用壳单元模拟,采用混凝土塑性损伤本构模型;梁、柱采用梁单元模拟,框架梁柱采用规范[25]给出的单轴混凝土本构,通过PQ-fiber子程序[26]中UConcrete03实现;钢筋采用PQ-fiber子程序中USteel02材料本构,即随动硬化单轴本构模型、再加载刚度按Clough 本构退化;砌体填充墙材料采用杨卫忠提出的砌体受压本构模型[27],砌体填充墙等效为斜撑[28]。其中考虑到箍筋的配置对结构变形的影响作用,建模时重点考虑了箍筋的实际工作状况,采用Mander 本构对核心区混凝土的材料参数进行修正[29]。
约束混凝土参数的修正方法如下:

地震振动台的试验结果与数值分析结果详细比较见文献[29],试验结果与模拟结果具有良好的一致性,表明建模方式准确,可以较好地模拟结构整体动力时程响应。
2.3 分析用地震波
地震易损性分析时选取了ATC-63远场22条地震记录,同时考虑到本文的研究对象是中国大陆地区的既有建筑,因此根据ATC-63远场选波原则选取了汶川地震中的江油波和什邡八角波,共计24 条地震波。
分析时将24条地震波峰值加速度分别调幅至18 gal、35 gal、50 gal、70 gal、100 gal、125 gal、140 gal、200 gal、220 gal、300 gal、400 gal、620 gal共12个幅值,对应于6度、7度、8度、9度区的三水准设防地震加速度峰值。
这样针对5个结构模型、24条地震波和12个幅值,组成1440个样本进行易损性分析及数据统计。
3 地震易损性分析
3.1 最大层间位移角反应统计规律
众多的研究表明,随机地震动作用下的结构响应服从对数正态分布[30−33],本文对五个结构的最大层间位移角进行对数统计,结果显示在相同的地震动强度作用下结构最大层间位移角服从自然对数正态分布,对数均值误差为0.9%,标准差在7%以内。
图10为8度中震和8度大震各结构的最大层间位移角对数正态分布概率曲线,竖向虚线从左至右分别对应弹性轻微损伤L2(1/550)、中等损伤L5(1/100)、严重损伤L6(1/50)和倒塌L7(1/30)。
从图10还可以看出,在8度中震作用下五个版本的结构均进入到弹塑性损伤阶段,但01版结构、10版结构对于中等损伤的超越概率明显降低,地震响应分布范围更加集中。8度大震作用下,原型结构、78版结构、89版结构对于严重损伤限值的超越概率很大,对于倒塌限值的超越概率不容忽视,但01版和10版结构完全可以实现大震不倒塌,并且对于严重损伤限值的超越概率也明显减小。
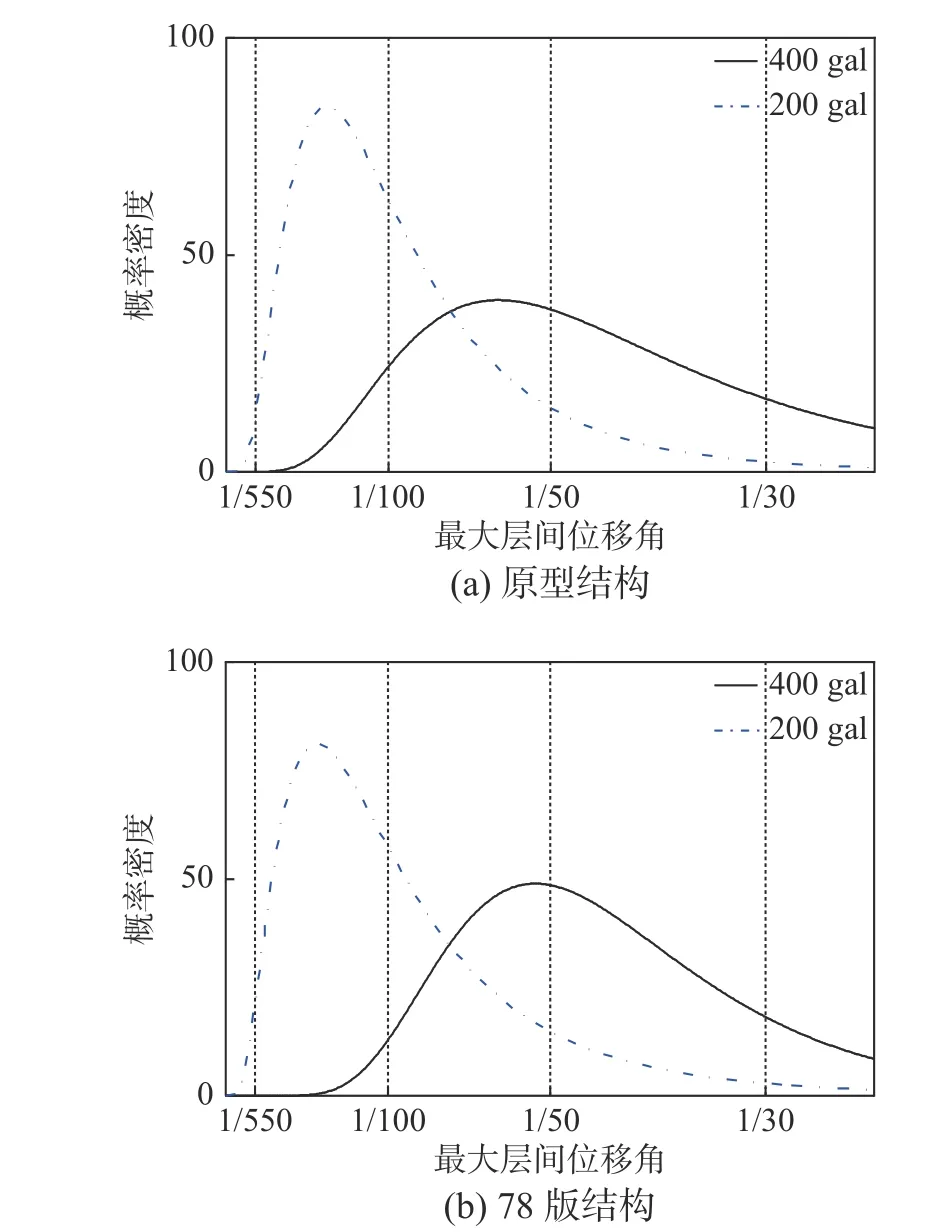
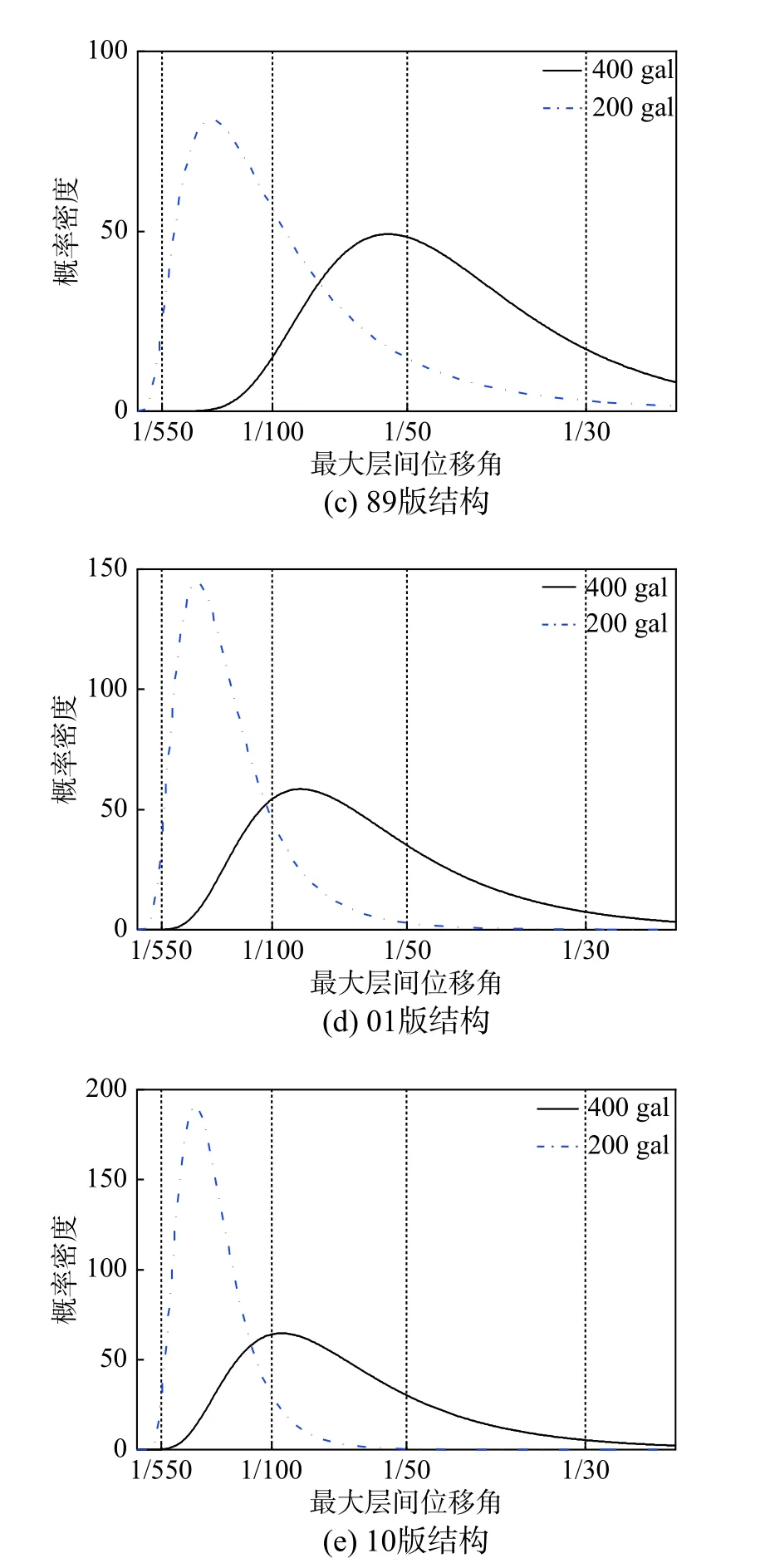
图10 最大层间位移角对数正态分布曲线Fig.10 Lognormal distribution curveof maximum drift
3.2 地震易损性函数的建立
地震易损性是指结构在不同强度地震动作用下结构响应超越指定损伤状态限值的概率。根据表1关于损伤程度的量化标准定义,以及结构在不同强度地震动下最大层间位移角对数统计均值和标准差,可以求得结构在不同强度地震动下各损伤状态的超越概率:

表1 既有框架结构抗震性能水准Table 1 Seismic performance level of existing RCframe
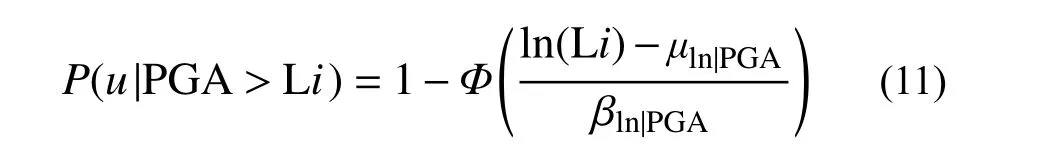
式中:µln|PGA、βln|PGA为地震动强度为PGA 时,结构最大层间位移角的对数平均值和对数标准差;Li为表1中性能水准i对应的层间位移角上限值;Φ 为标准正态分布函数
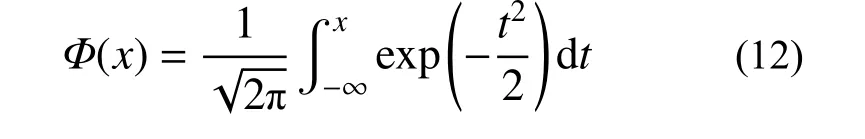
考虑到地震中结构的倒塌是多因素耦合共同作用下的结果,既有老旧建筑这种情况更为明显,为避免因倒塌样本引起的易损性曲线计算结果变异,本文对式(11)进行了改进,将倒塌项单独分离,易损性曲线计算公式成为以下形式:
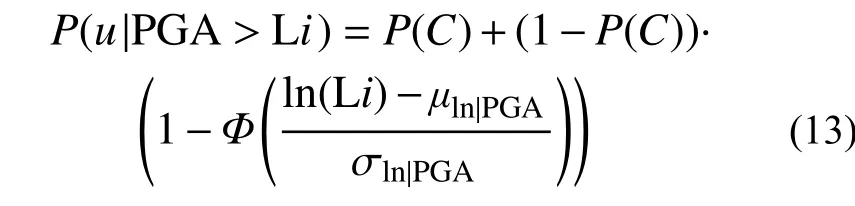
式中,P(C)为地震动强度为PGA 时分析结构出现倒塌的概率。
3.3 不同历史时期建筑的易损性分析
根据式(13)可以计算出基于损伤界限值的地震易损性曲线,见图11。
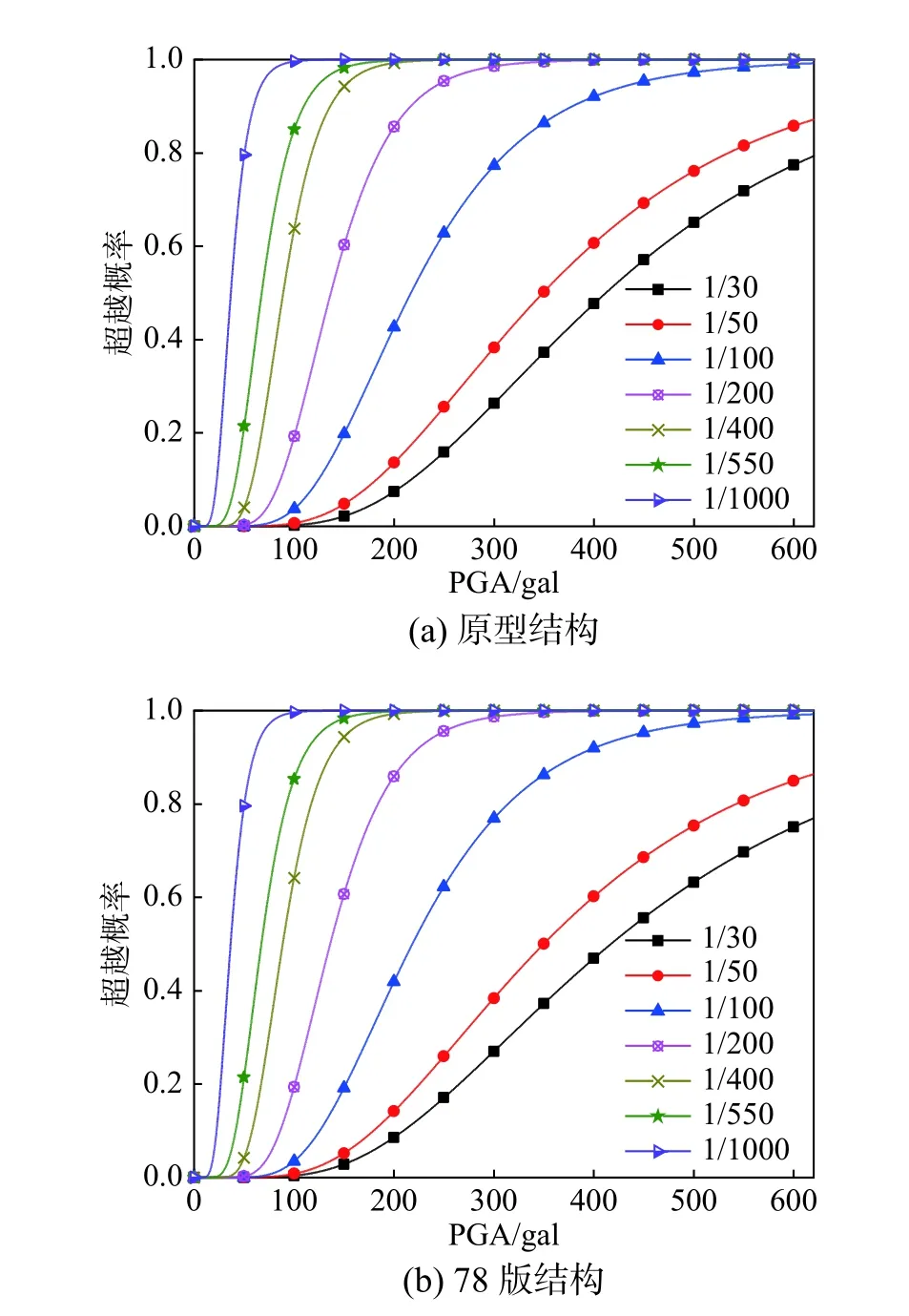
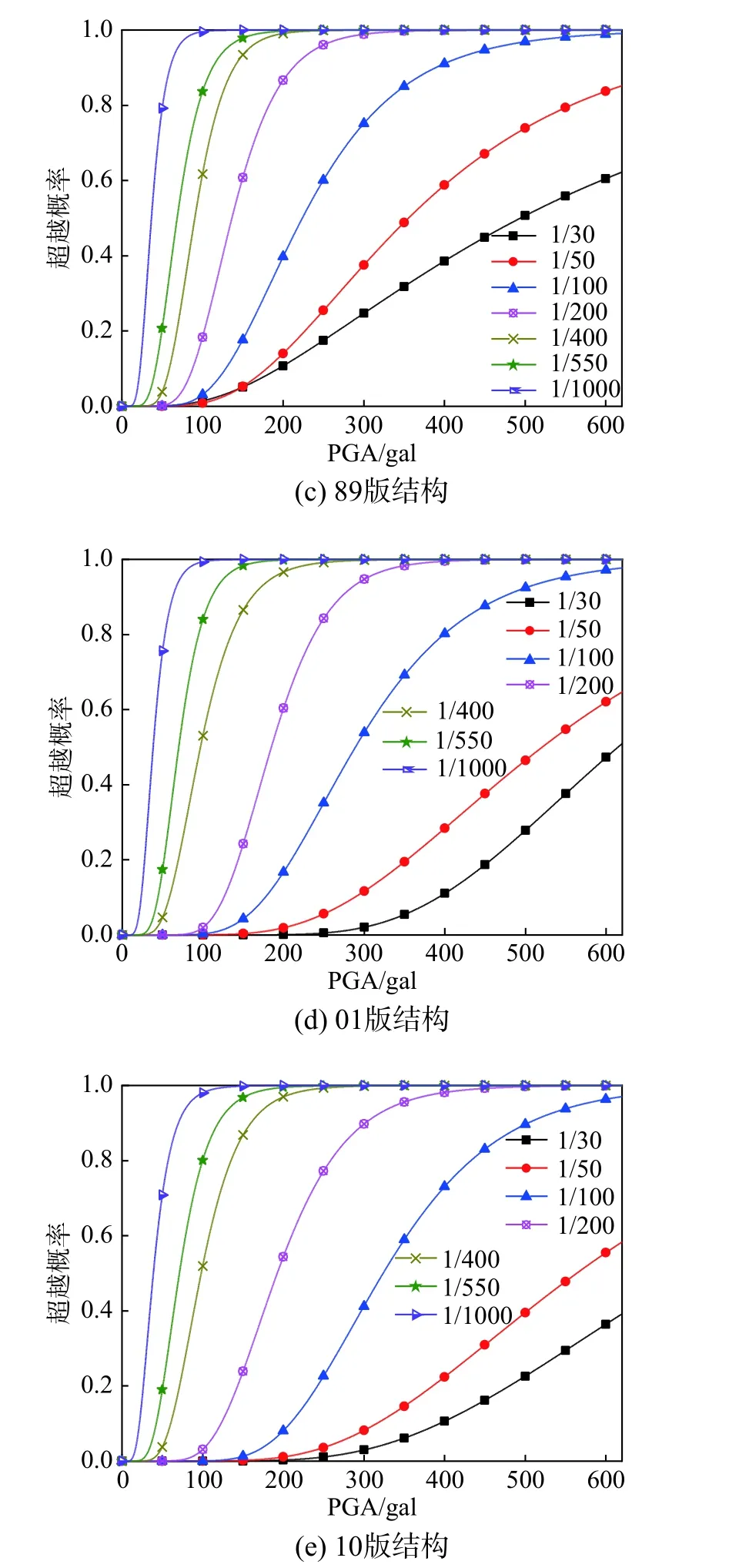
图11 不同年代结构易损性曲线Fig.11 Vulnerability curve of structuresat different ages
每一幅图对应一个分析结构,每一条曲线对应一个损伤界限值,横坐标为地震动强度,纵坐标为损伤界限值的超越概率。
易损性曲线是结构抵御指定损伤状态的广义抗震性能累积概率分布,反映了地震强度与损伤程度之间的关系。由图11可以看出,7 条易损性曲线将图形分成8个区域,从左至右依次对应性能水准L0~L7。从非结构构件损伤界限到倒塌界限,易损性曲线逐渐趋于平缓。随着地震强度PGA 增大,结构损伤程度趋于严重,倒塌概率也随之增加。
若采用超越概率小于50%作为满足性能水准阀值,不同历史时期建筑的抗震性能具有以下特点。
1)性能水准L0~L3
原型结构、78版结构、89版结构的易损性曲线变化不大;01版结构、10版结构在混凝土、钢筋强度等级和配筋构造上逐步提高,结构抗震性能略有提升。
2)性能水准L4
原型结构、78版结构的易损性曲线变化不大,89版结构抗震性能有所提高,约在7度大震下层间位移角接近1/100,01版结构、10版结构抗震性能较89 版结构进一步提高。
3)性能水准L5
原型结构、78版结构的易损性曲线变化不大,89版结构抗震性能有所提高,约在8度大震下层间位移角接近1/50,01版结构、10版结构抗震性能则提高得更明显,约在8度(0.3g)大震下层间位移角接近1/50。
4)性能水准L6、L7
原型结构、78版结构的易损性曲线变化不大,均具有较高的超越概率,89版结构接近于9度大震不倒的目标,01版结构、10版结构完全能够实现9度大震不倒的目标。
总体上看,我国不同历史时期的建筑在“小震不坏”的设防水准上相差不大,“中震可修”的可行性随着标准的修订逐步有所提高,“大震不倒”的设防水准则有较大的提高。
4 震害指数分析方法
4.1 震害指数计算方法
地震易损性分析曲线可以直观清晰的给出不同PGA 下结构基于损伤界限值的超越概率,为性能化抗震鉴定提供依据。然而采用该方法的计算工作量大,对于建筑群的抗震性能评估显然并不合适。在性能化鉴定时,如果能给出不同强度地震下描述结构损伤程度的量化指标,则更直观也更具有说服力。震害指数是目前众多描述结构地震中损伤程度的指标之一,也是目前震害研究中较为常用的分析指标。以往的震害指数分析均是在构件层面上采用确定性的计算方法,考虑到地震的随机性和既有建筑的复杂性,因此本文提出采用基于概率的震害指数法对结构损伤状态进行量化表达。
单体结构震害指数计算步骤如下:
1)建立结构地震易损性矩阵[PPGA,Li]
地震易损性矩阵形式如表2所示,行代表不同的地震动强度(共18个幅值),列代表不同的性能水准(共8个水准),矩阵中的每个元素则表示在对应的地震动强度下按式(11)计算的对应性能水准的超越概率。
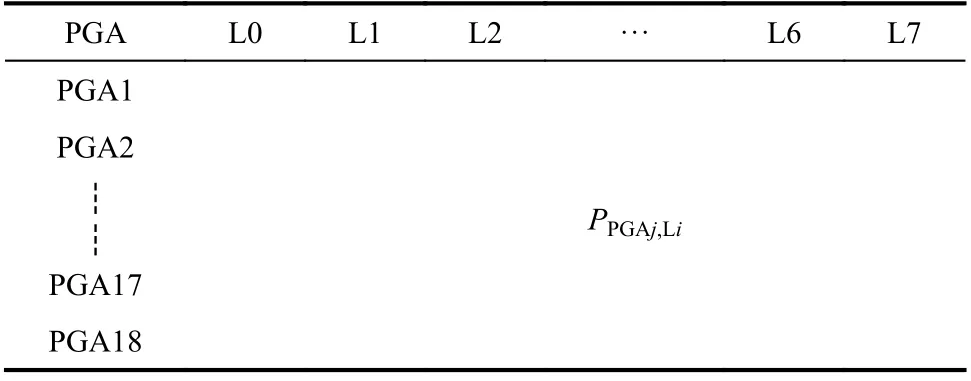
表2 地震易损性矩阵Table 2 Matrix of seismic vulnerability
事实上对每个历史时期的建筑,其抗震措施差别不大,因此,地震易损性矩阵中的各元素的值差别也不会太大,如果有足够数量的建筑采用地震易损性分析,基本可确定各元素PPGAj,Li的值,在设定超越概率的阀值后,就可直接对结构在预期地震作用下的损伤程度进行预测。
在目前缺乏足够统计样本数量的情况下,可暂采用震害指数简化方法进行相应的预测。
2)确定各性能水准震害指数取值范围
震害指数是一个描述结构或构件在地震中损伤程度的无量纲指标,是震前预测或震后评估的重要参考依据,也可为灾后救援重建决策提供参考[34−37]。根据表1确定的性能水准,对8个性能水准进行归一化描述和定量表达,用0表示结构完好无损,1表示结构倒塌,依据各性能水准对应的位移角限值、相邻性能水准之间涵盖的性能状态、对应的变形区间大小及结构在该性能水准的稳定性,其余6个性能水准在0至1中间进行插值,形成8个性能等级区间。8个性能水准对应的震害指数取值范围见表3。
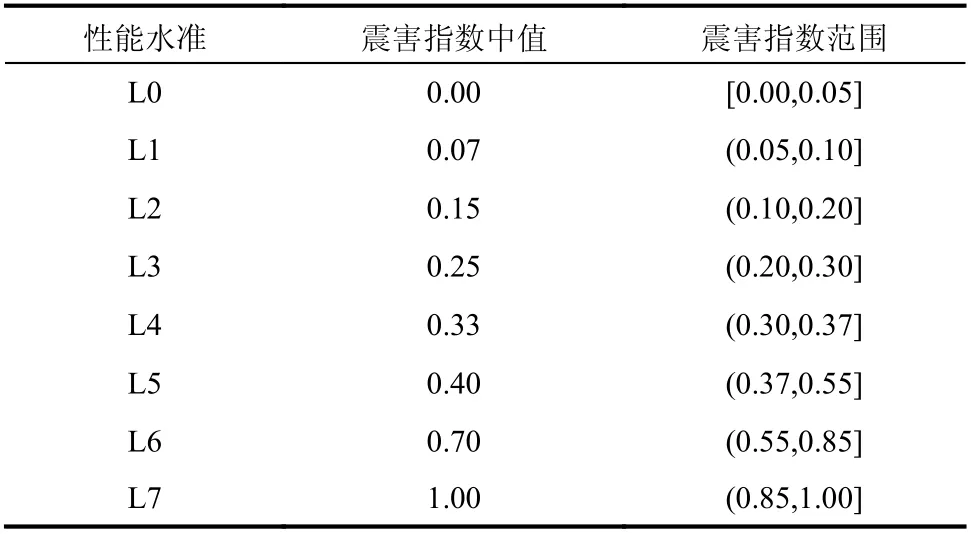
表3 震害指数表Table 3 Table of seismic damage index
3)单体结构的震害指数计算
单体结构的震害指数按下式计算:
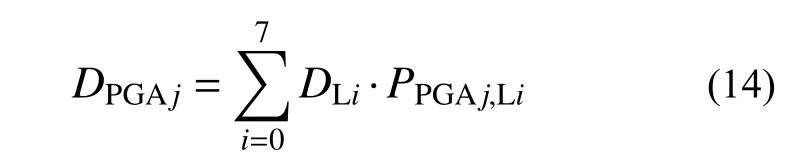
式中:DPGAj为地震动强度PGAj下结构的震害指数;DLi为表3中对应于性能水准Li的震害指数中值;PPGAj,Li为表2中对应于地震动强度PGAj、性能水准Li的超越概率。
4)根据DPGAj值对照表3中的震害指数范围,即可确定所能达到的性能水准。
5 工程应用
5.1 工程概况
某博物馆展览大楼建于1958年,位于8度抗震设防区。展览大楼为4层钢筋混凝土框架结构,首层地上高度8.7 m,其他层高均为8 m,总高度达35.45 m,构件混凝土强度实测结构首层为C 40、其余层为C30。该展览大楼的主要问题箍筋直径小、间距偏大,此外框架柱截面小、抗侧刚度不满足。加固前的结构平面图见图12。
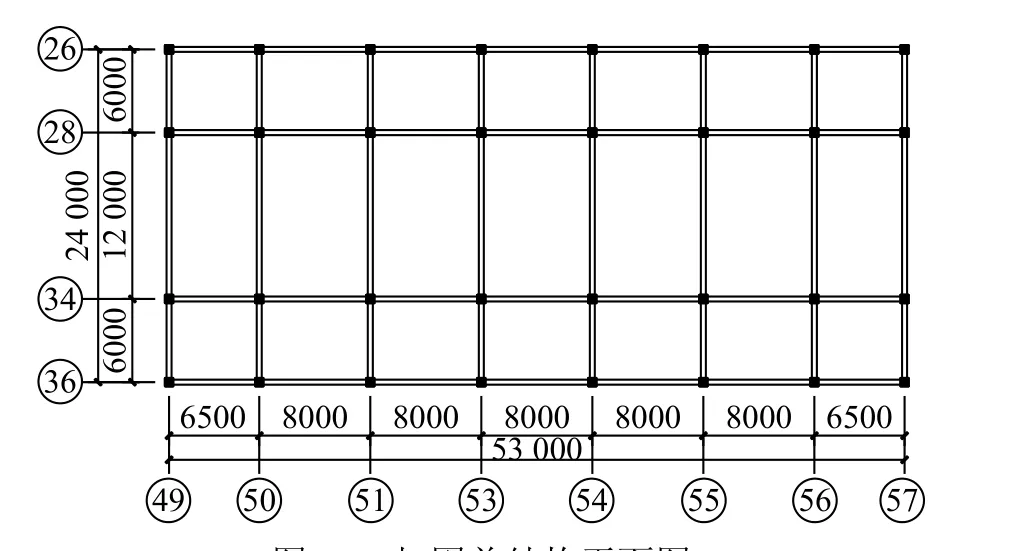
图12 加固前结构平面图Fig.12 Layout of the structure before strengthening
抗震加固的目标是达到后续使用年限50年和重点设防类建筑的要求,这是迄今为止要求最高的既有大型公共建筑的抗震加固设计。同时抗震加固不能破坏军博大楼的原有建筑风貌,尽可能减少对馆内使用功能的影响,同时最大限度减少原有构件的加固工作量,避免对每根梁、柱及节点进行加固。
经多方案多次技术论证比较后采用了增设壁式框架的加固方案,该方案保持建筑外立面不变,对内部布展和人流影响也减小到最低程度。加固后的结构平面见图13,图中涂黑部分是新设的壁式框架柱(柱宽450 mm、柱高600 mm),与原框架柱连为一体,原有框架梁静力不足的仍采用常规方法进行加固。
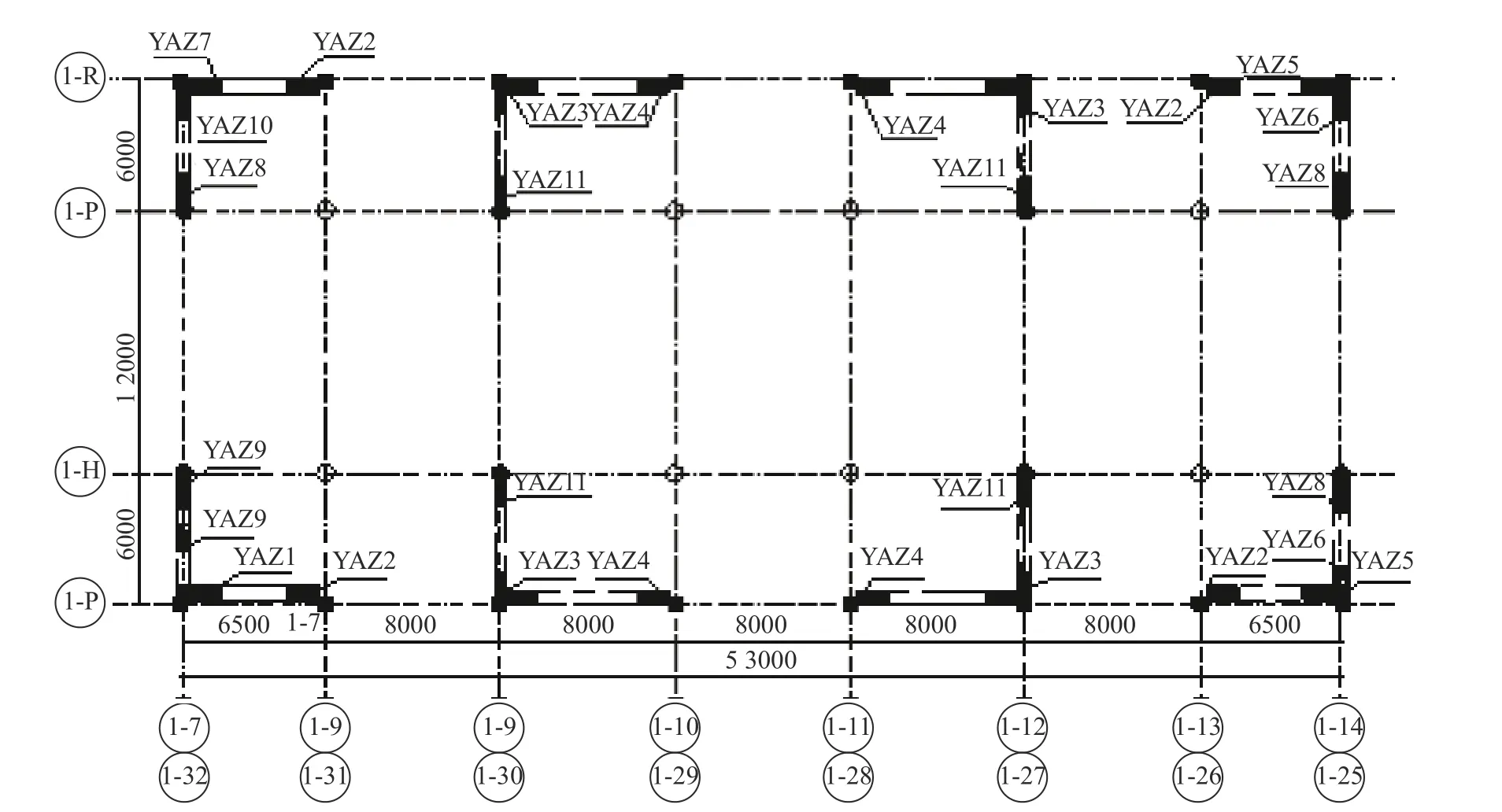
图13 加固后结构平面图Fig.13 Layout of thestructure after strengthening
由于抗震加固前后并未改变结构体系,因此采用本文提出的性能化抗震鉴定方法对抗震加固前后的性能进行评估,校核抗震加固是否达到了预期的设防目标,计算时考虑到后续使用年限50年的要求,地震作用未按文献[29]的要求进行地震作用折减。
5.2 性能化分析结果
按本文前述方法进行了结构地震反应分析与统计、地震易损性分析及震害预测。因该工程位于8度抗震设防区,现仅列出按8度设防和9度大震的主要分析结果。
5.2.1抗震加固前的地震易损性矩阵
从表4可见加固前:在8度小震作用下,结构的性能水准处于L3~L4的超越概率较大,将产生弹塑性损伤或更严重的损伤,不能达到“小震不坏”的设防目标;在8度中震作用下,结构的性能水准处于L4~L7的超越概率较大,将产生中等损伤倒塌超越概率也达到了22%,不可忽视,显然结构不能达到“中震可修”的设防目标;在8度大震作用下,结构的性能水准处于L5~L7的超越概率较大,其中倒塌概率已达到65%,不能实现“大震不倒”的设防目标,而9度大震的超越概率达到了87%,大震作用下倒塌无疑。
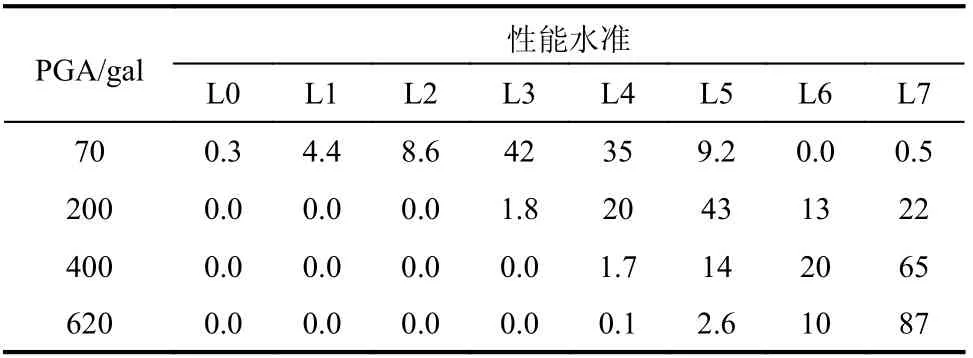
表4 结构加固前的地震易损性矩阵/(%)Table 4 Matrix of vulnerability before strengthening
5.2.2抗震加固后的地震易损性矩阵
从表5可见,加固后:在8度小震作用下,结构的性能处于L0超越概率很大,达到“小震不坏”的设防目标;在8度中震作用下,结构的性能处于L1~L3超越概率较大,震后稍加修复即可恢复使用,达到了“中震可修”的设防目标;在8度大震作用下,结构的性能水准主要为L3~L4,尚未达到中等损伤状态,仅需对个别构件进行加固,达到了“大震不倒”的设防目标;即便是在9度大震的情况下,其性能水准仍与8度大震相近,只是损伤程度略有增加,可以达到“大震不倒”的设防目标,从这个意义说,已经达到了8度乙类建筑的设防目标。

表5 结构加固后的地震易损性矩阵/(%)Table 5 Matrix of vulnerability after strengthening
5.2.3抗震加固前后的震害指数对比
从抗震加固前后震害指数对比同样可以看出(表6),加固后的震害指数大大降低,性能水准明显提高,在预期地震作用下的结构抗震性能与地震易损性的分析结果一致。
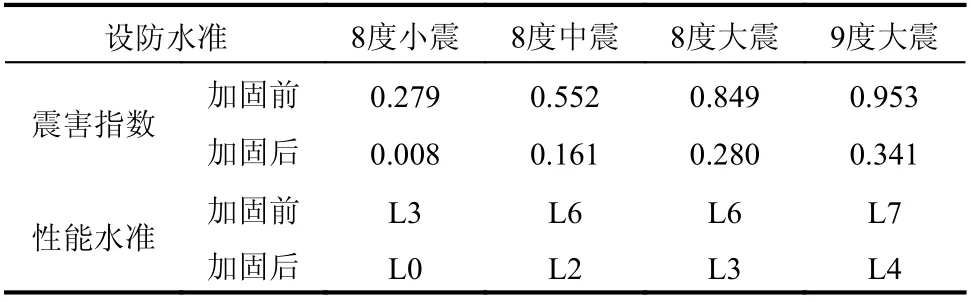
表6 震害指数与性能水准对比表Table 6 Comparison of seismic damage indexsand performancelevels
6 结论
本文针对既有大型公共建筑建立了基于性能的抗震鉴定方法,主要有以下几点结论:
(1)提出了以层间变形为控制指标作为既有建筑抗震性能水准的划分标准,分完好无损L0、非结构构件损伤L1、弹性轻微损伤L2、弹塑性轻微损伤水准L3、损伤L4、中等损伤L5、严重损伤L6和倒塌L7共8个性能水准。
(2)对我国5个历史时期的既有建筑,采用24条地震波、12个加速度幅值共1440个样本进行了地震响应分析,分析中特别考虑了既有老旧建筑箍筋间距偏大对混凝土的约束效应的影响。
(3)对1440个样本的地震位移响应进行了数理统计,给出了基于概率的兼顾倒塌因素的地震易损性函数,避免了统计参数变异性过大的缺点,在此基础上建立了地震易损性矩阵。
(4)引入震害预测采用的震害指数方法,基于易损性分析结果,提出了采用基于概率的既有建筑震害指数的量化表达方法。
(5)以某工程为例对本文提出的方法进行了校核,结果表明采用地震易损性分析方法与震害指数分析方法,两者结果一致。
