火灾下平行钢丝束温度膨胀及高温蠕变试验研究
2021-08-27严芙蓉
杜 咏,严芙蓉
(南京工业大学土木工程学院,南京211816)
在预应力张拉钢结构中,预应力钢索通常处于较高的应力状态,火灾发生时,由温度以及应力引起的钢索的热膨胀及高温蠕变效应将导致结构抗力退化,使得结构构件失效甚至结构整体倒塌[1]。因此,开展火灾高温下预应力钢索的高温蠕变性能试验研究十分重要。
目前,国内外学者对不同生产工艺制作的钢索及钢丝的高温力学性能开展了一系列高温试验研究以及理论分析。Maurice等[2]对预应力钢丝进行了高温蠕变试验,发现高温下蠕变将削弱预应力钢丝的预应力,但未给出相应的蠕变模型。Harmathy 和Stanzak[3]抽取1725级预应力钢绞线的中丝开展了高温蠕变试验,得到了中丝的高温蠕变曲线,并对Dorn[4]在1954年提出的高温蠕变理论进行了改进。John 等[5]使用数字图像相关方法(简称DIC),对预应力钢丝开展了稳态和瞬态蠕变试验,并在Harmathy 和Stanzak 高温蠕变模型的基础上,提出了新的蠕变参数。张昊宇和郑文忠[6]采用MTS试验机、高温应变引伸计及SF62高温炉,对高温作用下直径为5 mm 的1770级预应力钢丝的温度膨胀和高温蠕变性能开展了试验研究,得出预应力钢丝的高温膨胀应变随温度变化的规律以及高温蠕变计算模型。周焕廷等[7]采用炉体外测试方法,对直径为15.24 mm 的1860级预应力钢绞线进行了高温蠕变性能测试,基于试验数据拟合出了钢绞线高温蠕变方程。
钢索高温材性试验按测试方法不同可分为炉外测量和炉内测量。炉外测量技术所测变形为试件平均应变,此种测量技术已逐渐被各国学者弃用。炉内测量技术又分为直接测量与间接测量,直接测量使用的高温引伸棒与试样表面极易发生相对滑移,间接测量要求竖向引伸转化杆与试样的纵轴线保持平行,故以上测量方法均存在不足。由于测试手段的限制,以往试验多数采用抽取钢绞线中丝的方法进行高温蠕变试验,该方法未考虑在高温作用下钢绞线整体会发生反向扭转这一现象对钢绞线高温力学性能指标的影响。
基于上述问题,周浩等[8]采用非接触测量式应变视频测量系统[9],对1860级预应力钢绞线开展了温度膨胀试验和高温蠕变试验,提出了与试验结果吻合度较高的温度膨胀系数计算式和高温蠕变模型。文献[10]指出,火灾高温下,当忽略高温蠕变时,预应力钢绞线由于达到其极限强度而破坏;当考虑高温蠕变时,由于蠕变加剧了钢索的松弛变形,预应力钢绞线不会发生强度破坏,而是达到其断裂应变而破坏。而且,钢绞线的钢丝缠绕效应显著影响其力学性能。因此,高温蠕变应变在结构抗火性能分析中不能被忽略。
在单向拉伸试验中,平行钢丝束中钢丝破断状态与单根钢丝的破断现象基本一致,高温下单根钢丝与平行钢丝束的力学性能均会退化,但钢丝束的高温力学性能指标比单根钢丝的力学性能指标退化更为严重[11−12]。此外,平行钢丝束的成型工艺区别于钢绞线。钢绞线由多根高强钢丝向一个方向呈螺旋形均匀绞捻30°~45°而成。而平行钢丝束将若干根直径相同的高强钢丝平行并拢、扎紧,绞捻2°~4°而成。相对于钢绞线,平行钢丝束具有较高的弹性模量,且能够单向抗拉。故本文对常用于实际工程中的平行钢丝束进行温度膨胀及高温蠕变试验,提出相应的热膨胀应变及高温蠕变模型,服务于平行钢丝束在火灾高温下的力学响应分析。
1 试验概况
1.1 试件规格及制备
目前,国内常用19根×5 mm 和7根×7 mm 这两种规格的平行钢丝束。已有研究表明,平行钢丝束中钢丝的直径和数量对其高温力学性能均无较大的影响[13]。因此,本文采用如图1所示的1670级7根×7 mm 平行钢丝束为研究对象,试件的长度由试验机拉伸空间和高温炉尺寸综合确定,其几何特征如表1所示。在平行钢丝束试件中部喷涂白色耐高温漆,形成如图2所示的散斑带,作为记录标距位移的信息载体。

图1 1670 MPa 平行钢丝束试件Fig.1 1670 MPa tensile strength parallel steel wires

图2 试件表面散斑标记Fig.2 Speckle marking on surface of specimen

表1 平行钢丝束试件几何特征Table 1 Geometric properties of parallel steel wires
1.2 试验装置
本文的试验装置如图3所示,整个试验系统由加载系统、温控系统以及测量系统组成。其中,Instron 液压伺服万能试验机的最大加载能力为500 kN。高温炉炉膛净尺寸为30 cm×10.5 cm(高×直径),由3个加热单元组成,可以对三个单元同时加热以保证全炉升温均匀,最高温度可达1250 ℃。CCD相机可记录材料表面散斑图的变化,并将位移变化量以灰度矩阵的形式输入到计算机中。非接触式应变视频测量系统如图4所示,可通过软件实时分析,输出试件标距段的位移及应变随温度的变化历程。

图3 试验装置Fig.3 Test setup
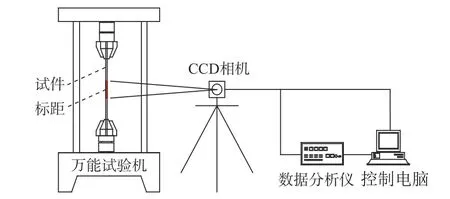
图4 非接触式应变视频测量系统Fig.4 Measurement system of non-contact video gauge
2 温度膨胀试验
2.1 试验方法
进行高温下平行钢丝束的自由膨胀试验前,需将图1所示试件一端锚头切除;如图5 所示,用双头螺杆将试件上锚杯与试验机加载端连接,将试件下端套入位于试验机底座正中心的定位套筒内,并在套筒内壁涂润滑油,将套筒与底座固定,使平行钢丝束试件下端既可以沿纵轴线变形自由又沿轴线保持对中[14]。

图5 平行钢丝束自由端定位套筒Fig.5 Positioning sleeveat free end of parallel steel wires
试件安装完后,在炉内部分的索体纵向表面上、中、下三段绑扎热电偶,检测试件表面的实时温度。用防火棉填充炉体上、下端部空隙,确保炉内温度的稳定性与均匀性。对平行钢丝束试件进行升温,升温速率为10℃/min,使炉内温度从室温分别升温至100℃、150℃、200℃、250℃、300℃、350℃、400℃、450℃、550℃、600℃、650℃、700℃、750℃、800℃,并在各温度水平恒温20 min~30 min,以保证各温度水平下钢索截面温度分布均匀。当视频引伸仪的应变读数稳定时,读取相应温度水平下的热膨胀应变值。在每个温度水平下重复对3根钢索试件进行测试并记录应变值。共计开展了15个温度水平下平行钢丝束热膨胀应变的测定。
2.2 试验结果及分析
考察如图6所示的平行钢丝束热膨胀应变随温度变化关系,可以发现,平行钢丝束热膨胀应变随着温度的升高呈非线性增长;温度为750℃左右时,平行钢丝束热膨胀应变从1.0253%突降到0.9241%,产生这种现象是因为在温度为750℃左右时,钢丝束的微观结构发生了变化,表现为相变。本文的平行钢丝束是以铁素体+渗碳体(珠光体,索氏体,贝氏体)为原始组织的高碳盘条,其化学成分为C、Mn、Si、Cr、Ti、V。随着相变的发生,其原始组织会奥氏体化。奥氏体有不同于铁素体和渗碳体的晶格结构,奥氏体的原子致密度高于铁素体和渗碳体,故相变会引起试件体积的收缩。且相变引起的收缩量远大于升温引起的热膨胀效应,因此在750℃时热膨胀应变值会突然降低。当奥氏体化趋于完全后,随着温度的升高,热膨胀应变值也会升高。这是由于奥氏体的线膨胀系数是铁素体和碳渗体线膨胀系数平均值的2倍。故在750℃~800℃,主要由奥氏体受热引起试件的热膨胀应变又突然增大。
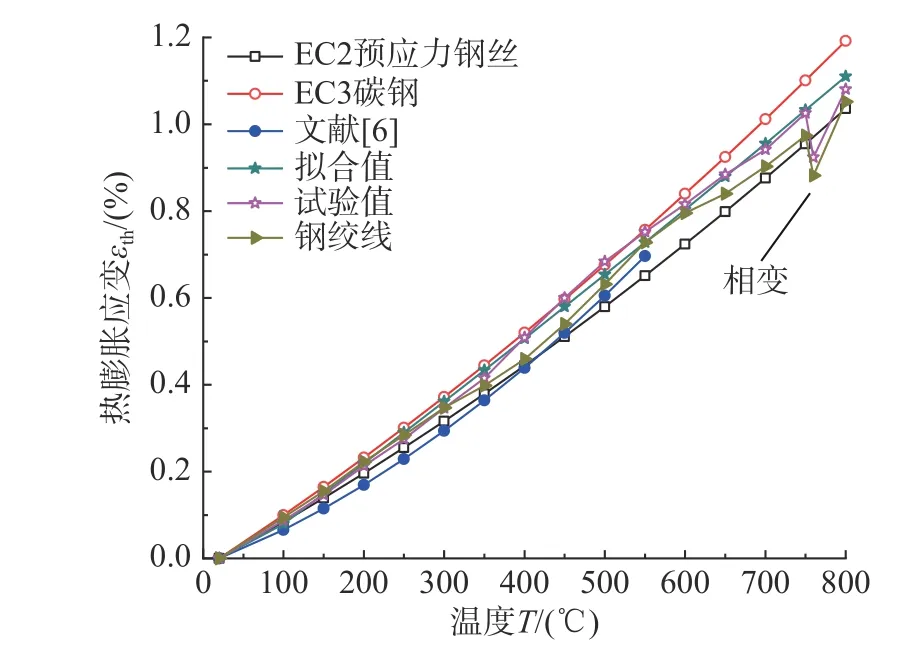
图6 热膨胀应变与温度关系曲线Fig.6 Curvesof thermal expansion strain versus temperature
平行钢丝束在15个温度水平下的热膨胀应变如表2所示。将表2试验数据绘制在图6中,与已有成果对比发现,预应力平行钢丝束与钢绞线的热膨胀应变随着温度的升高的趋势相同,平行钢丝束的热膨胀应变值略大于钢绞线热膨胀应变值,两者最大相差0.0608%。EC3[15]建议的碳钢的热膨胀应变值较平行钢丝束热膨胀应变试验值大0.1767%,这是由于碳钢微观组织的硬度较预应力钢丝的小,即碳钢抵抗变形的能力较预应力钢丝弱,故在相同应力水平下,碳钢会产生更大的热膨胀应变[16]。
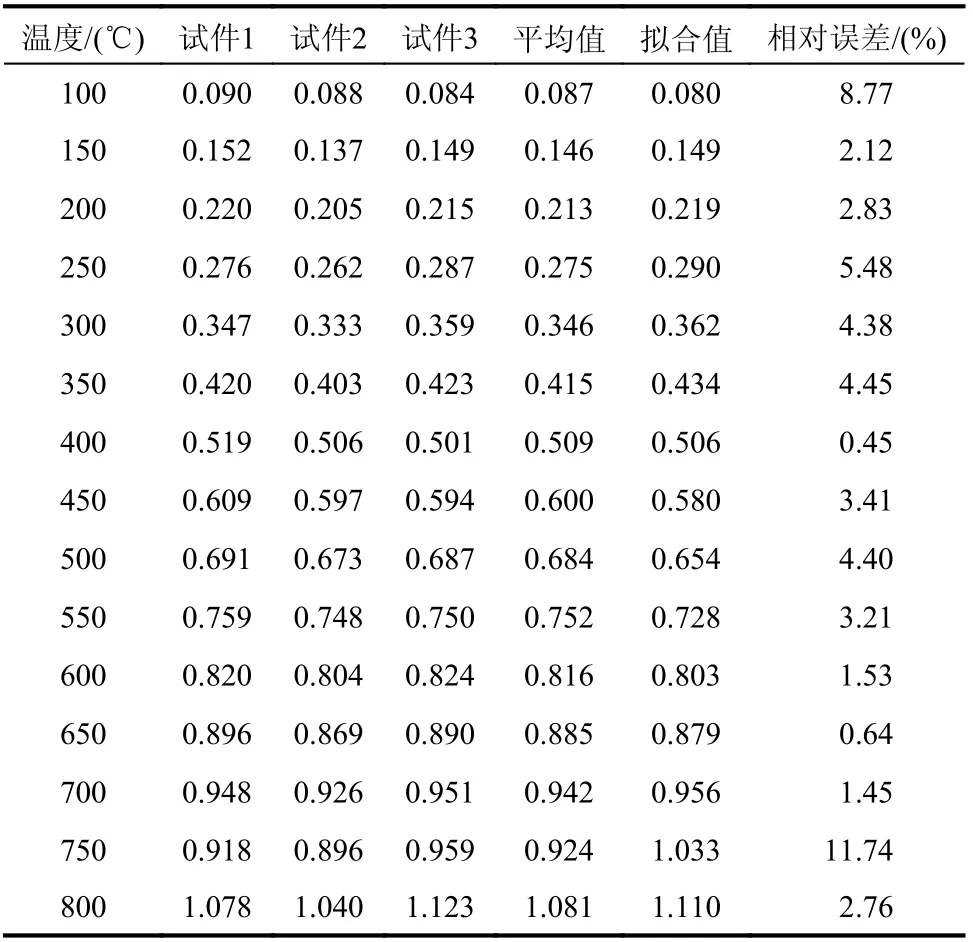
表2 平行钢丝束温度膨胀应变试验值Table 2 Experimental data of thermal expansion strain of parallel steel wires
2.3 热膨胀系数与温度函数
根据文献[17]对金属材料热膨胀系数的定义,热膨胀系数是对关于温度的热膨胀应变函数求一阶导得到的。在此,本文首先对表2中平行钢丝束的热膨胀应变试验平均值采用一元回归分析法拟合得到其关于温度的二次多项函数式(1):

3 高温蠕变试验
3.1 试验方案
《金属材料单轴拉伸蠕变试验方法》(GB/T 2039−2012)[18]中指出,温度和应力是影响平行钢丝束高温蠕变性能的重要因素,故需在不同温度和应力条件下开展高温蠕变测试。
根据文献[19]可知,蠕变的试验温度通常取0.3~0.5金属熔点(绝对温度),镀锌钢丝束的熔点为1545℃。故本文高温蠕变试验温度水平取350℃、400℃、450℃、500℃。
由于高温蠕变在应力水平低于金属屈服强度下显著发生,所以高温蠕变试验应力水平由钢丝束所处温度下的屈服强度决定。根据文献[20]中试验数据,确定各温度水平下的f2%,T屈服强度如表3所列。本文先取0.5f2%,T作为工况1的应力水平,观察工况1的蠕变应变发展情况,进一步确定工况2和工况3应力水平。
试验采用恒温加载方法[18],以10℃/min 升温至预定温度水平后恒温30 min 再加载。由于高温蠕变是随时间变化的量,所以加载过程应尽量快,以避免在加载过程中产生过多的高温蠕变变形[21]。因此,在恒温后10 min 内平稳施加拉力以达到表3的应力水平。当拉力达到预定值后,保持拉力恒定,以5 Hz 采集频率,记录高温蠕变应变随时间的变化历程,记录时间为2 h。每种工况测试1根试件,共计测试了12根试件。

表3 平行钢丝束高温蠕变试验参数Table 3 Test parameters of high temperature creep of parallel steel wires
3.2 试验现象
图7为预应力平行钢丝束在表3所列各温度和应力水平下,经历2 h 高温蠕变试验后,试件自然冷却到常温时的外观。考察图7发现,平行钢丝束在高温蠕变试验中均未发生明显颈缩变形。与钢绞线类似,平行钢丝束的蠕变效应同时受温度水平和应力水平的影响,温度越低,平行钢丝束可以承受的蠕变应力水平越高;反之,随目标温度的升高,蠕变应力水平降低。

图7 预应力钢丝束高温蠕变试验后外观Fig.7 Appearanceof parallel steel wiresafter high temperature creep test
3.3 试验结果分析
各温度及应力水平下平行钢丝束的高温蠕变应变曲线分别如图8和图9所示。
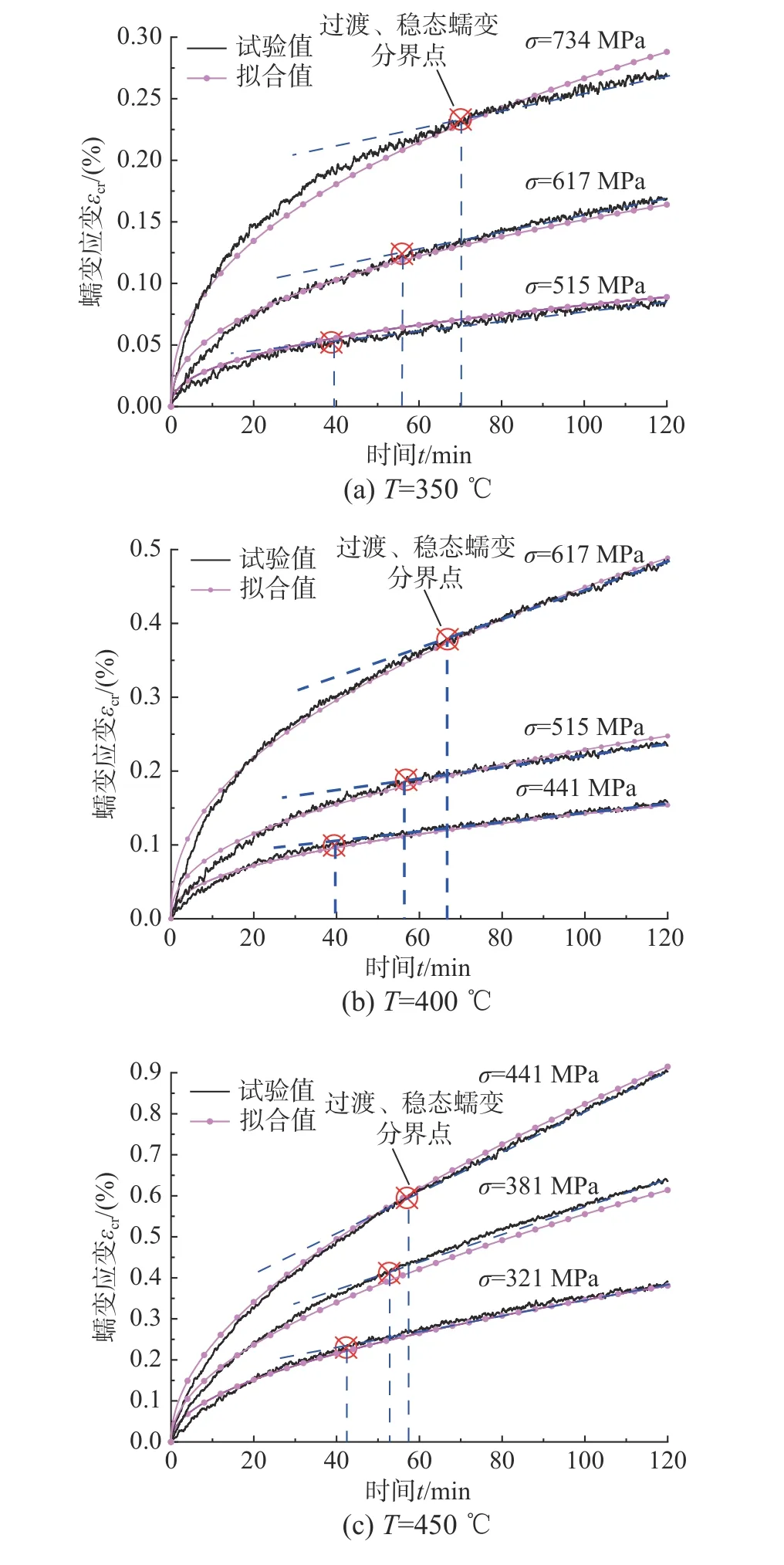
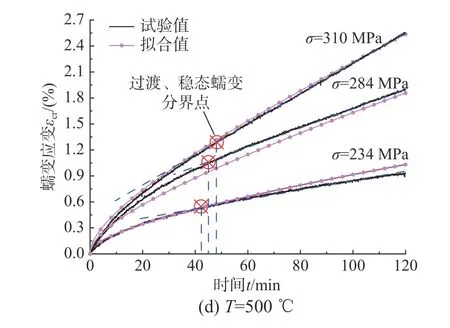
图8 应力水平对平行钢丝束高温蠕变应变历程的影响Fig.8 Effect of stress level on creep strain curves of parallel steel wires
本文将蠕变应变增长速率逐渐减小并过渡到保持恒定的分界点作为蠕变分界点,记作“⊗”。蠕变分界点将蠕变历程分为2个阶段:第一阶段为过渡蠕变阶段,该阶段的应变增长速率随着时间的增加而不断减小;第二阶段为稳态蠕变阶段,该阶段的应变速率大致稳定,蠕变速率变化较小,这是由于变形引起的加工硬化与动态恢复速率达到了平衡[22]。
应力水平对平行钢丝束蠕变历程的影响如图8所示。图8(a)中,历经2 h的350℃高温,应力水平为515 MPa、617 MPa 及714 MPa 对应的蠕变应变分别达到0.0863%、0.1689%及0.2692%。从图8(a)中稳态蠕变阶段曲线的斜率来看,随着应力水平增高,曲线斜率越大,稳态阶段蠕变增长越快;在应力水平为515 MPa 时,历经约40 min进入稳态蠕变阶段,当应力水平提高到617 MPa和734 MPa 时,分别延长至55 min 和70 min 进入稳态蠕变阶段。图8(b)~图8(d)的蠕变历程变化规律与图8(a)相似,即在温度水平一定时,平行钢丝束高温蠕变应变及稳态蠕变增长速率均随着应力水平的增高而增大,且进入稳态蠕变阶段的历时延长。此外,对比图8(a)~图8(d)可以发现,随着温度水平的升高,蠕变应变差值增大,这种现象表明,温度水平越高,应力水平对蠕变性能的影响越显著。当温度水平为500℃时,较低的应力水平也能导致平行钢丝束产生较大的高温蠕变应变。
温度水平对平行钢丝束蠕变历程的影响如图9所示。图9(a)中,在应力水平为441 MPa 下,分别历经2 h 的400℃和450℃高温,蠕变应变值分别达到0.1572%、0.9026%,两种温度条件下的蠕变应变差值为0.7454%。在图9(b)中,在应力水平515 MPa 下,分别历经2 h 的350℃和400℃高温,蠕变应变差值为0.1479%;而在图9(c)中,当应力水平为617 MPa 时,受温度影响的蠕变应变差值为0.3172%。总体上,相同应力水平下,随着目标温度升高,高温蠕变应变以及稳态阶段蠕变增长速率均会增大,且进入稳态蠕变阶段前经历的时间越长。当温度为450℃时,平行钢丝束的蠕变速率和蠕变增长速率均突然增大,因此在400℃~450℃,平行钢丝束高温蠕变表现出显著的转变。
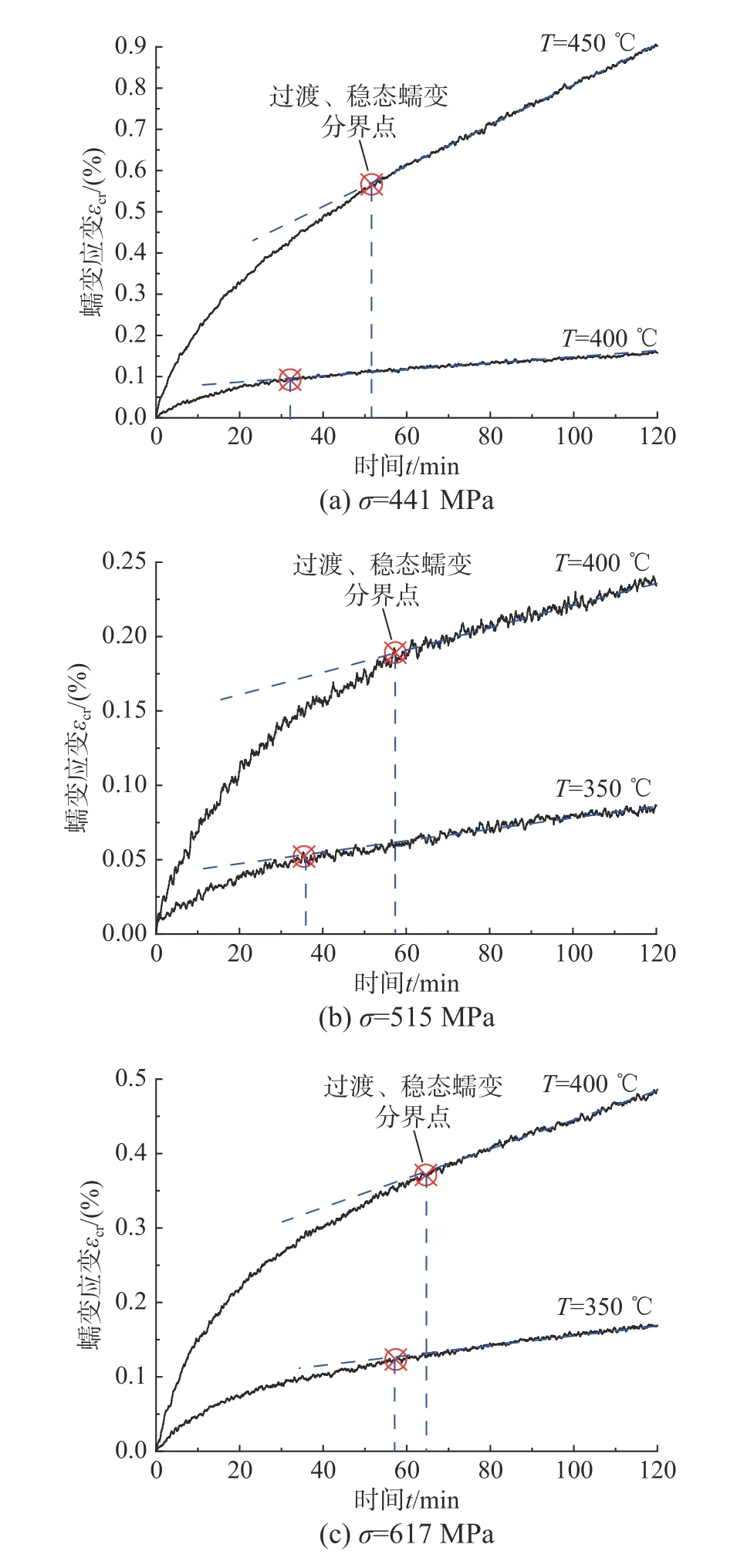
图9 温度水平对平行钢丝束高温蠕变应变历程的影响Fig.9 Effect of temperature level on creep strain curvesof parallel steel wires
将平行钢丝束与钢绞线的蠕变历程进行对比。如图10所示,当应力水平为441 MPa、温度为450℃时,历经2 h 升温历程的钢绞线的蠕变应变比平行钢丝束大29.8%;当应力水平为284 MPa,目标温度为500℃时,钢绞线的蠕变应变远大于平行钢丝束。在应力水平和温度水平相同的条件下,由于钢绞线的缠绕效应,钢绞线的蠕变效应高于平行钢丝束的蠕变效应,故平行钢丝束的高温蠕变应变显著小于钢绞线。
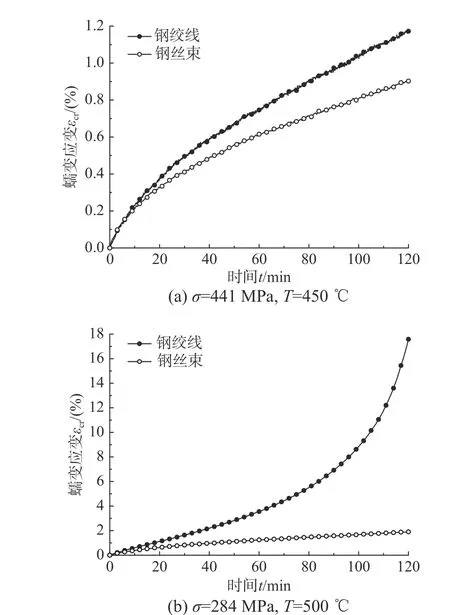
图10 钢绞线与平行钢丝束高温蠕变应变历程的对比图Fig.10 Comparison of high temperaturecreep strain between twisted and parallel steel wires
3.4 高温蠕变应变计算模型
各温度及应力水平下,高温蠕变随时间的变化量均不相同,因此,难以建立通用方程来计算不同参数条件下的高温蠕变应变。
基于Zienkiewicz和Cormeau 关于塑性和蠕变的统一理论提出的复合时间强化模型[23]是ANSYS中的第11种蠕变模型,如式(3)所示:

该模型可模拟第一、第二高温蠕变阶段,第三阶段预示着试件即将失效破坏,故不作分析。
式(3)中的待定参数较多,难以确定适合各温度和应力水平的拟合系数。从试验结果来看,温度为450℃时,蠕变速率和蠕变增长速率均突然增大。故以450℃为界,利用1stopt 软件对本文的试验数据进行分段拟合,得出适用于不同温度及应力水平下高温蠕变方程的拟合系数如表4所示,R2>0.99,故拟合度很高,拟合结果如图8(a)~图8(d)所示。本文提出的高温蠕变模型适用于高温下预应力平行钢丝束的力学响应数值模拟。

表4 平行钢丝束高温蠕变模型拟合系数Table4 Fitting coefficients of high temperature creep model for parallel steel wires
4 高温蠕变后平行钢丝束的抗拉强度
对历经2 h 高温蠕变且尚未断裂的平行钢丝束进行了抗拉强度试验研究,平行钢丝束的破断情况如图11所示。经受高温蠕变后的平行钢丝束破断位置位于试件经历过高温的中间段。这表明钢丝通过冷拔工艺获得的强度增强,在历经高温后受到削弱。

图11 平行钢丝束单向拉伸试验破坏特征Fig.11 Damage characteristics of uniaxial tensile strength test of parallel steel wires
图12为平行钢丝束在各应力和温度水平下经历2 h 高温蠕变后,自然冷却到常温后的抗拉强度。结果表明,平行钢丝束经历高温蠕变后的抗拉强度,随着经历的蠕变试验温度的升高呈现明显的衰减趋势。在310 MPa 应力水平下,经历500℃后,试件的抗拉强度的最小值为1213.69 MPa,与常温极限强度相比衰减30%;在相同的条件下,钢绞线抗拉强度衰减达40%。将本文的试验数据与文献[24]的退化公式对比发现,温度越高,试验值与文献[24]计算结果偏差越大。说明随着温度的升高,高温蠕变应力水平对剩余抗拉强度影响变得更加显著。高温蠕变试验温度为500℃时,应力水平对历经高温后的平行钢丝束抗拉强度的影响幅度达9%。
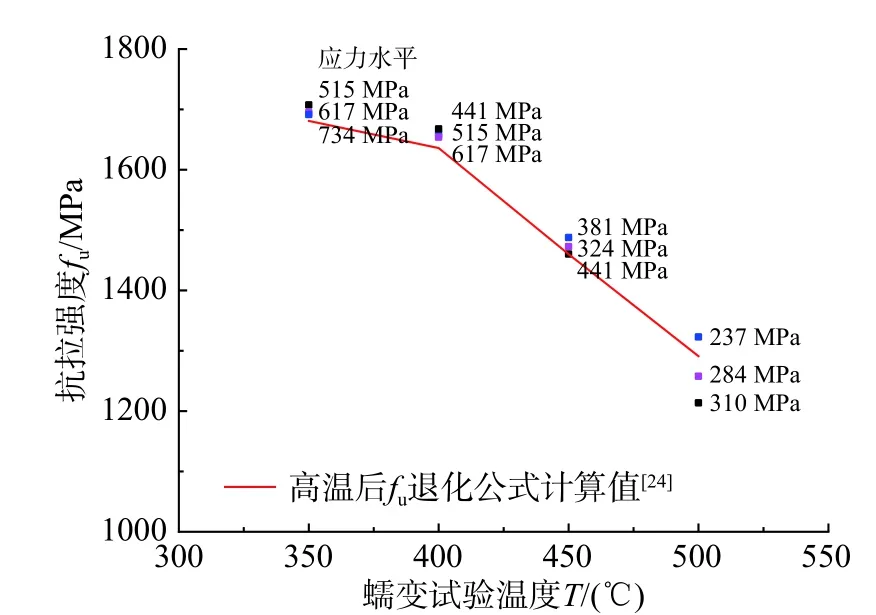
图12 高温蠕变后平行钢丝束的抗拉强度Fig.12 Tensile strength of parallel steel wires after high temperature creep
综上所述,随着历经的温度水平的升高以及应力水平的增加,历经高温蠕变自然冷却后的平行钢丝束的抗拉强度衰减显著,这表明火灾后钢索的承载能力有显著衰减。
5 结论
本文对1670级平行钢丝束进行了热膨胀及高温蠕变试验,提出了与试验数据吻合较好的热膨胀系数计算式,以及适用于数值分析方法的复合时间强化蠕变模型,并得出以下规律:
(1)在750℃左右,平行钢丝束材料发生相变,微观结构发生奥氏体化,热膨胀应变变小,奥氏体化趋于完全后,热膨胀应变值又会突然增大。
(2)温度及应力水平都会对平行钢丝束的高温蠕变历程产生影响。蠕变应变随着温度水平及应力水平的升高而增大。相同温度及应力水平下,平行钢丝束的蠕变应变比钢绞线的小。蠕变速率和蠕变应变增长率在450℃时均会突然增大,蠕变速率转变温度在400℃~450℃。
(3)历经2 h 高温蠕变性能试验,自然冷却到常温后的平行钢丝束试件的抗拉强度最大衰减30%;且高温蠕变试验温度愈高,应力水平对历经高温后平行钢丝束的剩余抗拉强度的影响愈大。
