公路工程现浇箱梁横梁计算研究

杜海洋 赵 航

郑州市交通规划勘察设计研究院（450000）

0 引言

目前城市基础设施建设正如火如荼的开展，城市快速路普遍采取预应力连续现浇箱梁的结构形式。现浇箱梁具有诸多优点，断面布置灵活，适用跨径范围广。城市快速路应统筹地面交通组织，桥墩布置要兼顾桥下空间利用，因此横梁的布置往往有较多类型，诸如门架型，单悬臂型及双悬臂型等。双悬臂型横梁断面及预应力布置多采用图1形式。横梁的受力较为复杂，准确计算需要借助空间实体有限元模拟，相对费事，不利于工程设计采用，目前多采用平面杆系单元近似计算，精度可以满足工程需求。濮辉铭[1]对一联3×30 m，箱梁宽25.2 m的预应力钢筋混凝土高架桥建立了全桥实体模型，荷载为自重和车道荷载，通过对横梁支座一定范围内应力积分，分别求出恒载和活载下支座反力。另外建立平面杆系模型，简化横梁计算。通过三种不同等效方法计算，对比实体模型计算的结果，选出较为准确的平面杆系模型。文章结论认为，将横梁两侧有效宽度范围内恒载按照均布荷载施加于横梁上，将剩余恒载按照腹板面积比例分配给腹板的近似方法与实体模型最为接近。金波[2]对一联3×30 m，桥梁宽20 m，箱梁为单箱四室，双支座的的预应力钢筋混凝土桥进行了空间实体单元分析。详细研究了主梁向横梁传递剪力分布规律，结论认为中横梁边缘截面腹板区域分配到的剪力占截面总剪力约85%，各个腹板之间剪力相差约为5%，靠近支座附近腹板剪力偏大一些。文章同时对比了三种平面杆系简化计算方法，认为将纵梁传递过来的剪力作为外力平均分配给各个腹板与实体单元模型误差最小，并且安全系数偏保守。

1 恒载剪力传递的简化处理

对于一联3×30 m预应力钢筋混凝土桥梁中横梁的计算比较具有代表性，常规高架桥方案标椎跨径多在30 m左右。目前相关研究主要体现在纵梁剪力在横梁上分布规律研究。研究的方法主要有空间实体有限元法，梁格法和简化的平面杆系法。空间实体有限元法是将结构离散为有限个的梁单元，研究各单元的性质，形成单元刚度矩阵；然后“集零为整”，按照结构的几何条件及平衡条件将各个单元集合成原来的结构，形成总体刚度矩阵，求得到结构的位移和内力[3]。常用的软件有ANSYS等，求得各个节点的应力后通过积分求出区域的剪力，这种方法与实际受力最为接近，但前期建模对设计人员要求较高，后期处理难度也较大，常用于研究教学。梁格法相对于空间实体有限元法，前处理和后处理难度都降低不少，利用Midas Civil可以较方便建立模型与分析计算。平面梁格意思是将桥梁划分成平面网格，桥梁结构的纵向刚度等力学性能有纵向梁格承担，横向刚度等力学参数由横向梁格承担，纵横向梁格在交点处公用节点。问题的关键是如何对刚度进行取值，遵循的原则是原结构与对应的梁格在相同荷载作用下，二者的挠曲是相等的，这种近似处理的精度满足结构计算要求。箱梁的梁格划分纵向可以腹板为对象划分，在Midas Civil梁格建模助手中可以较好处理刚度等效问题。横向可以在横隔板间距位置设置，横向梁格的刚度采用横隔板刚度和横梁的刚度，应允许考虑翼缘有效宽度。计算结果可以直接查看各个腹板传至横梁的剪力等内力，相比单梁模型，梁格模型的计算稍显麻烦，梁格的划分是否合理对设计人员的要求较高[4]。平面杆系模型在梁格法基础上进一步简化，将纵梁简化为梁单元，每个节点六个自由度，先建立纵向单梁模型，施加荷载和作用后，计算出支座反力，由于单梁模型横向的简化，无法直观分析横向各个腹板间剪力的分配规律，这种规律一般可借助前两种方法的案例统计规律。在单梁模型中，横梁的计算模型根据剪力滞的影响确定两侧翼缘有效宽度，将横梁模型单独抽离出来建立单梁模型，（如图2所示）。根据纵梁模型中的支反力及分布统计规律，在横梁上施加外荷载进行分析计算。在这个简化过程中做了两个主要的近似处理，一方面是腹板剪力的分布规律是一个粗糙的近似，在设计中为了节约建模时间和保证一定安全度，采用合理的近似方法至关重要。另一方面横梁的边界条件处理相对粗糙，横梁边缘截面在荷载作用下，会有剪力、弯矩和轴力等主要作用。支点截面处负弯矩影响根据桥梁跨径等会有较大变化，体现在横梁边界条件上是沿着横梁跨径方向左右各一对分布力矩，横梁左右力矩差值较大时，横梁截面的扭矩就会较大，在计算中是不可忽略的。

常规的箱梁根据腹板与顶底板节点的相对刚度，腹板间距等影响因素，箱梁在外荷载作用下受力极为复杂，近似于并列的T型截面，由于顶底板的约束，各个T型截面之间相互耦联，在靠近横梁段，由于横梁的刚度较大，各个T型截面顶板变形受到三边较强约束，剪力的传递只考虑腹板会有一定误差（如图1所示）。平面杆系模型是一种理想化的处理方式，近似认为横梁的刚度对各个T型梁肋的剪力传递不影响。先计算纵桥向恒载工况，求出横梁下部支座反力。单独把横梁作为计算模型，将支座反力按照一定方法施加于横梁上。这种简化计算方法简单，利用工程设计。在支座反力分配上往往有不同的理解，濮辉铭和金波的研究方法都认为腹板承担了主要剪力，前者认为横梁的有效宽度和跨径会影响比例系数，后者认为这些影响是次要的，在双支座布置中腹板承担100%剪力是可以满足工程设计精度的，而且偏安全。

图1 计算简图（m）

在常规桥梁设计中，从概念设计出发，为了防止剪压脆性破坏，增加梁的延性，可以遵循“强剪弱弯”的原则。箱梁腹板宽度在靠近支座一定范围内，厚度约为跨中段1.75倍，设置箍筋加密区，在荷载增加至临界点时，横梁边缘截面会发生应力重分布，腹板应力逐渐趋于均匀，顶底板的剪应力较小，对于梁端转动具有良好支持，因此金波的结论与概念设计更加吻合。

2 活载剪力传递的简化处理

活载在平面上分布，分布工况较多，为了简化处理，主要是将二维平面问题转化一维杆件计算问题，根据边界条件建立杆件受力模型计算分析。上部箱梁桥面板受到车轮荷载，荷载首先传递至两侧腹板，腹板将力传至两侧桥墩处横梁，横梁将腹板处传来的荷载及自重传递至支座，所有上部荷载通过支座传至下部结构。因此横梁的荷载主要是计算腹板传至横梁的集中力。桥梁整体化计算采用车道荷载计算，将上部结构简化为一个连续梁杆件，计算自重工况下最不利荷载产生的“支座”反力N，根据公式（1）将N作为荷载施加于横梁上（如图2所示）；计算一个车道工况下产生的“支座”反力P，折算出车辆荷载，根据实际车道数在横梁上进行横向布载（如图3所示），根据影响线求出活载作用下截面内力。

图2 恒载分配

图3 活载分配

这种活载计算方法的主要是解决腹板间剪力分配和车道布置的相关性。20 m宽桥梁上可以布置四个车道，四个车道横向布置有较多组合方式，先求出一个车道工况下横梁支反力，将反力作为荷载加载横梁上，同时布置四个车辆荷载，利用横梁影响线，求出横梁最大内力。

上述方法能较好对横梁的内力进行分析，精确度较高，一般情况下横向活载满布的工况下横梁的内力最大，各个腹板的剪力差值不大，近似采用恒载分布的简化方法。为了简化计算，不再对横梁上活载进行横向布载分析，而将总活载等效呈静载分配到腹板，考虑到车道横向布载的偏载工况，对边腹板分配系数适当放大，系数建议取1.3。恒载依旧均分至各腹板。该方法计算简便，误差在工程允许范围。

对于悬臂式横梁布置，计算原理类似，主要区别在于横梁的边界条件（如图4所示），墩梁采用固结形式。悬臂端与支点处挠度差异，会导致左右腹板受力差异较上述横梁边界条件下腹板较大。在工程设计中可以建立全桥模型，验算横梁的变形及内力，平面杆系模型应慎重选用。

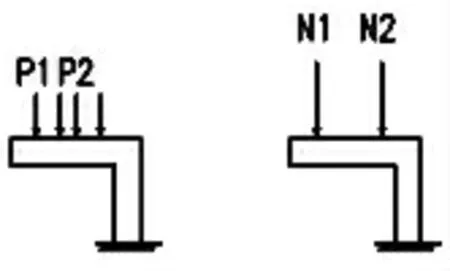
图4 悬臂式横梁计算简图

3 结语

现浇箱梁的横梁作为横向传力构件，在整个体系中扮演着重要角色。一方面对于箱梁的横向刚度贡献巨大，另一方面对于桥梁下部结构的布置起着重要作用。目前对纵梁传至横梁的剪力分布依然没有达成统一意见，相关系统性研究成果仍然欠缺。当前的研究对支座的布置数量对剪力分配的影响仍较少；斜腹板对剪力分配的影响仍较少；横梁采用固结边界条件对剪力分配的影响仍较少。

在工程设计中应注重概念设计，防止桥梁体系出现脆性破坏，可以遵循“强剪弱弯”原则，适当调大横梁边缘腹板剪力。