基于HYDRUS-2D的负压微润灌土壤水分运动模拟

徐俊增 刘玮璇 卫 琦 王可纯 王海渝 周姣艳

(1.河海大学农业科学与工程学院， 南京 210098；2.河海大学水文水资源与水利工程科学国家重点实验室， 南京 210098；3.昆山市城市水系调度与信息管理处， 昆山 215300)

0 引言

随着人口数量的增长和经济社会的快速发展，人均水资源可利用量不断锐减，水资源短缺问题已经成为制约我国经济发展的重要因素[1]。在水资源供需矛盾日益突出的背景下，发展新型节水灌溉技术对提高灌溉用水效率、缓解农业用水危机具有重要的现实意义[2]。

负压微润灌是一种通过土壤基质吸力将灌溉水由低处向高处运移而自动补充土壤水分、维持根区稳定土壤水分、以保证作物需水的灌溉方式[3]，其最主要的特点是连续微量供水、维持稳定的土壤水分分布[1]、减少地表无效蒸发和下渗损失，从而实现水资源高效利用[1,4]。负压微润灌技术具有节水、节能、促进作物生长、改善土壤环境等优势，是一种极具发展潜力的新型节水灌溉技术[5-6]。随着灌水器材料与制备工艺的日趋成熟，负压微润灌技术受到了越来越多的关注，但受供水压力、灌水器导水率及埋深等因素的影响，仍缺乏较为系统的负压微润灌技术设计标准或参考依据。因此，在实际推广应用中受到一定的限制[2]。

土壤湿润体决定作物的水分利用效率和生长特性[7]，准确把握负压微润灌的土壤湿润体特征，对于选择具有高效用水效率的负压微润灌技术参数具有重要指导意义。在诸多影响负压微润灌土壤湿润体特征的因素中，灌水器导水率KS、供水水头H及灌水器埋深D是决定负压微润灌湿润体特征的重要因子。在通常情况下，KS决定了负压微润灌的供水速率，KS越大，意味着水分进入土壤的通道越多，在相同时间内累积入渗水量和湿润体也越大[8]。H决定了灌水器的内外压力差，H越小，意味着土壤水吸力和湿润体越小[9-10]，一般认为，作物适宜的负压微润灌供水水头主要维持在-10～0 kPa范围内[2]。灌水器埋深也显著影响土壤湿润体的分布特征，是实现与作物根系有效匹配的关键因素[11]。

数值模拟方法可以定量描述土壤水分运动过程，因此被广泛应用于节水灌溉研究中[12]。由美国国家盐土实验室开发的HYDRUS模型具有模拟精度高、算法种类丰富等优点，是目前应用最为广泛的水分运动模拟模型之一[13-15]。已有学者针对该模型在负压微润灌条件下的土壤水分运移规律进行了模拟研究。冀荣华等[14]研究了不同灌水器半径(8、10、12 cm)对负压微润灌土壤水分入渗的影响，结果表明，灌水器半径是影响土壤水分入渗的显著性因素，且水分入渗速率随灌水器半径的增大而增加。WANG等[8]通过土箱试验与HYDRUS-2D模型相结合的方法研究了灌水器导水率、土壤初始含水率、灌水器埋深以及供水压力对土壤水分入渗的影响，并基于上述参数建立了负压微润灌累积灌水量的半机理半经验的数学计算表达式。目前，关于负压微润灌土壤湿润体的研究主要采用土箱试验和模型模拟相结合的方法，探究不同灌水器埋深和供水水头对湿润体最大湿润距离及其水分含量的影响[16]，而将负压微润灌土壤长期稳定的湿润体特征与作物根系分布特征相匹配，探求不同作物适宜的负压微润灌技术参数范围等方面的研究还鲜见报道。

本文以负压微润灌为研究对象，以3种负压控制下的土箱实测土壤水分数据为依据，通过反演土壤和灌水器水力特征参数构建基于HYDRUS-2D的负压微润灌模型，研究负压微润灌不同灌水器导水率和供水压力水头条件下土壤有效湿润距离(满足作物正常生长所需要的最低土壤水分的运移距离，包括水平距离、垂直向上距离和垂直向下距离)的变化规律，并结合负压微润灌不同情景模拟下土壤湿润体特征和典型设施作物根系分布特征及需水规律，探究常见设施作物适宜的负压微润灌技术参数范围。

1 材料与方法

1.1 数据来源

本试验于2019年4—6月在河海大学水文水资源与水利工程科学国家重点实验室(32°3′24″N,118°45′E)进行。供试土壤取自南京市蔬菜花卉科学研究所塑料温室，采集的土壤样本在自然条件下进行风干，经过研磨、过筛(4 mm)后分层填入规格为80 cm×40 cm×60 cm土箱内，填土高度为45 cm。供试土壤均源自表层(0～30 cm土层)土壤，其基本物理特征参数如表1所示。

表1 土壤基本物理特征参数

试验采用陶土管负压微润灌系统进行供水(图1)。其中负压微润灌系统采用顶空气压传感器测定内部压力，并通过单片机进行决策来控制排气泵对内部压力进行调整，使之稳定在设定的压力范围(-100～100 Pa)。试验采用黏土陶土管灌水器(外径3 cm，内径1.5 cm，长40 cm)进行灌溉，陶土管在回填过程中置于土箱长边一侧的中线位置处(埋深为15 cm)。试验过程中，土箱一侧用于记录不同时刻的湿润峰推进情况，另一侧用于取样测定不同时段和不同距离的土壤含水率，即取样侧在水平和垂直方向上每隔5 cm处设置取样孔(直径d为1 cm)。本研究中，选择灌水器周围的6个取土点为观测点，并采用不锈钢土钻(外径8 mm，内径6 mm)对土壤样品进行采集，采用干燥法(100℃，8 h)对土壤质量含水率进行测定，并通过土壤质量含水率与土壤容重的乘积求得土壤体积含水率。

试验共设置3个供水压力处理(供水水头H分别为-2、-4、-6 kPa，表示为T1、T2、T3)，每个处理设置3个重复。试验过程中，分别在灌水后第1天内的4、8、16、24 h，以及之后6 d内每间隔24 h记录湿润峰推进距离和土壤含水率。

1.2 模型构建

1.2.1数值模型

负压微润灌沿水平方向均匀入渗，假设土壤均匀且各向同性，在灌水器左右两侧轴对称，因此按照二维水分运动的理念进行模型概化，使用HYDRUS-2D对不同负压供水条件下的土壤水分运动进行模拟分析，其水分运动方程为Richards方程[15],即

(1)

其中

式中c(h)——比水容量(也称容水度)，cm3/cm3

θ——土壤含水率，cm3/cm3

h——土壤水压力，kPa

K(h)——非饱和土壤导水率，cm/min

t——时间，min

r、z——柱坐标下径向坐标和垂向坐标，cm

土壤水分入渗规律采用VG模型进行描述[12]，表达式为

(2)

(3)

其中

m=1-1/n

式中θs——土壤饱和含水率，cm3/cm3

θr——土壤残余含水率，cm3/cm3

θ(h)——土壤相对饱和度，cm3/cm3

KS——土壤饱和导水率，cm/h

Se——土壤相对饱和度

α——经验常数，与进气压力成反比

n——与孔径分布相关的经验参数

l——经验形状系数

1.2.2几何模型

由于陶土管灌水器管材为多孔材料，其水分运移理论上也可借助HYDRUS模型进行模拟，因此，在模型模拟过程中将陶土管假定为一种多孔材料(直径3 cm，厚度1.5 cm)。另外，考虑到土壤水分入渗过程土壤湿润体的左右对称性，本研究中仅针对土体右侧的湿润过程进行模拟[8]，即在模型构建过程中将厚度为1.5 cm的半环形陶土管灌水器设置在计算模拟区域的左侧，用于模拟其土壤水分在土体右侧运移规律，因此其坐标系的原点位于土体下边界的最左侧(图2)。此外，模型模拟过程中，考虑到上下层土壤容重的差异以及灌水器特殊的渗透性质，将模拟区域分为0～16.5 cm土层、16.5～45.0 cm土层和灌水器3部分，分别设置水力特征参数，并在模拟区域中根据取土样点的位置同步设定6个土壤水分观测点(图2)。

1.2.3边界条件设定

模型模拟区域为40 cm×45 cm的矩形，目标网格大小为1 cm，土壤剖面按深度分为0～16.5 cm和16.5～45.0 cm 2个土层。对于灌水器的多孔介质特性，为了使计算更加精确，在灌水器周围进行加密并按网格大小为0.25 cm进行划分，整个模型共划分成4 388个几何节点(图2)。灌水器内壁边界为定水头边界(Constant pressure head)，边界水头设定为实际压力水头，结合土壤初始含水率，通过土壤水分特征曲线获得土壤初始负水头为-20 000 cm[17]。忽略对称面的水平交换，左侧边界除灌水器外其余部分按不透水边界对待。上边界设置为大气边界(Atmospheric boundary)条件，由于试验在室内进行，不考虑降雨量和蒸发蒸腾速率日变化的影响，因此，平均潜在蒸发量设置为0.4 cm/d[8]。另外，考虑到试验模拟期间土箱装置的不透水性且在试验模拟期间水分基本不会入渗到底部和右侧边界，所以右侧和底部均设定为无通量边界(No flux)。

1.3 模型水力特征参数反演

模型模拟结果的可靠性通常取决于土壤或灌水器水力特征参数的选择。目前，关于水力特征参数的选择主要通过基于土壤基本物理特征参数的ROSETTA模型预测、基于实测土壤水分特征曲线计算以及基于实测含水率结果的反演模型计算得到。例如，ZHANG等[18]基于实测含水率数据和HYDRUS-2D模型反演并验证了反演模型的模拟精度，结果表明反演模型能够较好地模拟土壤水分运移特征，其均方根误差(RMSE)仅为0.015～0.038 cm3/cm3。此外，还有部分学者通过研究地下滴灌系统及地下排水系统的水分迁移过程，认为反演参数越少，反演模型的模拟结果越精确[16,19]。因此，为了得到与实测结果匹配性更高的模型，以往大部分文献主要先通过ROSETTA模型预测土壤初始水力特征参数，并选择其中的敏感参数基于实测结果进行反演计算，得到新土壤水力特征参数及反演模型，且证实了其模拟结果的可靠性[8,20-22]。

基于供试土壤的颗粒级配与容重，以HYDRUS-2D模型内置RETC预测模块估算土壤初始水力特征参数(表2)。并根据落差法(Falling head method)测量计算得到陶土管的饱和导水率KS0[22]。假设陶土管灌水器在试验初始阶段工作压力较小且处于饱和含水状态，故α取较小值0.000 001 cm-1。此外，假定管壁材料的不饱和参数θs、θr、n和l对模拟结果没有显著影响，其取值可借鉴SIYAL等[22]研究结果。

表2 土壤和灌水器初始水力特征参数

以T1(H=-2 kPa)处理实测的土壤含水率数据为依据对土壤水力特征参数进行反演计算，以T2(H=-4 kPa)、T3(H=-6 kPa)处理结果进行验证。基于土壤初始水力特征参数值，通过HYDRUS-2D内置Marquardt-Levenberg优化算法对土壤和灌水器参数θr、α、n和KS进行反演计算。考虑到反演参数的数量越多对模型精度的影响越大[19],因此，在参数反演过程中，重点针对陶土管较为敏感的参数饱和导水率KS0及土壤水分特征的敏感参数θr、α、n、KS进行了反演，反演参数的设置区间主要参考KARIMOV等[23]研究结果，其具体范围如下：KS0、KS为 0.000 1～5 cm/h，θr为0.35～0.6 cm3/cm3，α为0.003 1～0.036 8 cm-1，n为1.3～2.42。此外，在对反演结果进行精度分析时，土壤含水率采用6个观测样点的实测值与模拟值进行比较；累积入渗量由于模拟过程仅采用半柱体进行分析，故模拟值需加倍后再与实际灌水量进行比较分析，湿润距离(土壤水分的实际运移距离)则选取湿润体3个方向(水平方向、垂直向上方向和垂直向下方向)对不同时刻土壤实际观测的最大湿润边界及模型模拟值进行比较。

1.4 统计方法

为了评价模型的准确性，采用平均误差(ME)、均方根误差(RMSE)和纳什效率系数(NSE)3个指标对模型模拟结果进行评价。一般情况下，ME和RMSE越小、NSE越接近1，说明模型精度越高。

1.5 情景模拟

影响负压微润灌土壤湿润体特征的因素主要包括土壤质地、灌水器材料、供水水头、灌水器埋深等[2]，因此，在土壤质地和作物种类确定的情况下，灌水器材料和供水水头是影响负压微润灌土壤湿润峰最主要的因素。为进一步明确影响负压微润灌土壤湿润体特征的灌水器导水率和供水水头临界范围，本研究以土箱试验T1处理的负压微润灌技术参数为基础，通过HYDRUS-2D反演模型模拟负压微润灌不同灌水器导水率(0.000 1～0.005 cm/h)和不同供水水头(-10～0 kPa)条件下土壤湿润体分布特征，统计分析有效湿润距离(对应能够满足作物生长所需的最低土壤水分(本研究取0.15 cm3/cm3)的湿润距离)，建立不同灌水器导水率和供水水头与有效湿润距离之间的定量关系。并结合该定量关系，以典型设施作物主要根系分布特征和适宜的供水压力范围[2]为参考，通过设置不同负压微润灌技术参数组合，借助反演模型模拟更多情景组合下土壤湿润体特征。此外，为更好模拟原状土的特征以及考虑到实际回填过程中因夯土对灌水器产生的影响，本研究模型模拟过程中，以不同灌水器埋深D(5、10、15、20 cm)所对应的土层为临界土层，并分别将模拟区域临界土层上下部分土壤水力特征参数设定为基于HYDRUS-2D的负压微润灌水分模型反演后的上下两层(0～16.5 cm和16.5～45.0 cm)的土壤水力特征参数值。

2 结果与讨论

2.1 基于HYDRUS-2D的负压微润灌模型参数反演与验证

2.1.1模型参数反演

由土壤初始水力特征参数(表2)和模型反演参数结果(表3)可以看出，反演后的土壤水力特征参数KS较其初始值有了显著降低，即分别由1.064、1.041 cm/h降低为0.012、0.008 cm/h，而其余参数的变化相对较小。

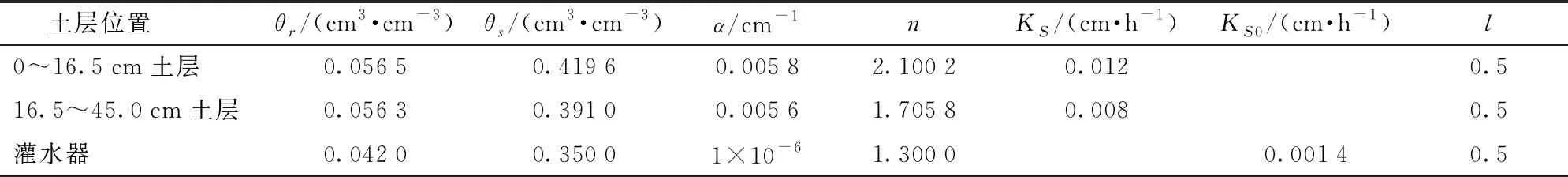
表3 反演后的土壤和灌水器水力特征参数

此外，基于土箱试验T1(H=-2 kPa)处理的实测数据对反演模型的准确性进行验证，相关评价指标结果见图3。可以看出，反演模型模拟的T1处理的土壤含水率、累积入渗量和湿润距离(水平距离、垂直向上距离、垂直向下距离)与实测结果之间具有较好的一致性，其决定系数(R2)均达到了0.98以上，ME分别为0.37 cm3/cm3、0.09L和1.09 cm，RMSE分别为3.49 cm3/cm3、0.22L和1.73 cm，NSE分别为0.910 8、0.951 2和0.778 5。结果表明，HYDRUS-2D模型能够较好地模拟负压微润灌土壤水分运移特征。

2.1.2模型验证

为进一步验证反演模型对负压微润灌不同负压状态下模拟结果的精度，针对验证数据T2(H=-4 kPa)和T3(H=-6 kPa)处理对模拟结果进行了分析(表4和图4)。结果表明，反演模型对T2和T3处理的模拟结果与实测结果之间的R2均达0.98以上，NSE均在0.77以上，ME和RMSE虽较T1处理有所增大，但均在可接受范围内。研究结果还发现，随着负压微润灌供水压力的减小，反演模型对土壤含水率的模拟值与实测值之间的误差越小，而累积入渗量和湿润距离模拟结果与实测结果之间的误差则越大。整体上，反演模型对负压微润灌不同供水水头条件下的土壤水分运移特征(含水率、累积入渗量和湿润距离)均具有较高的模拟精度，可以作为模拟更多灌水器参数组合下土壤水分动态的工具。

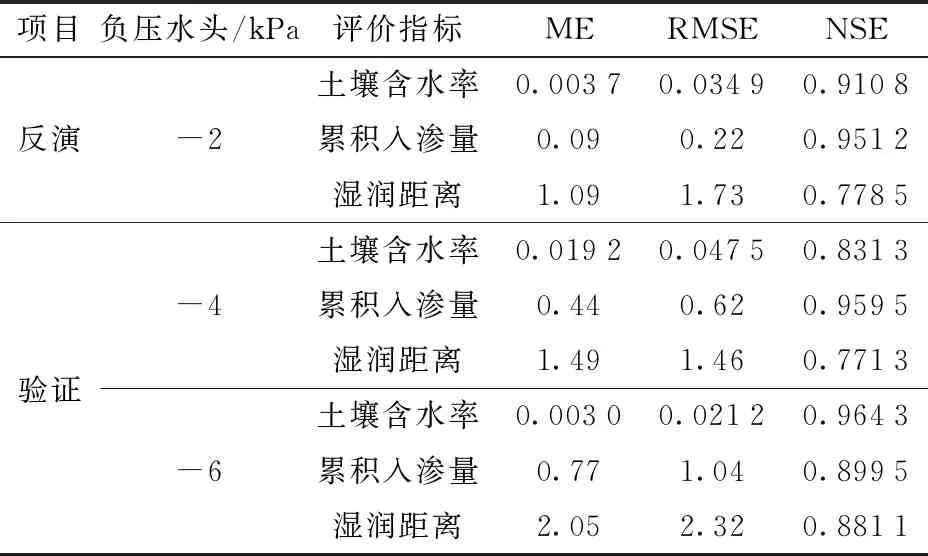
表4 模拟值与实测值的误差分析

2.2 基于HYDRUS-2D的负压微润灌模型应用

2.2.1负压微润灌技术参数范围选择

通过反演模型对不同灌水器饱和导水率(0.000 1～0.005 cm/h)的土壤湿润体特征的模拟结果(图5，**表示差异极显著)可以看出，灌水器饱和导水率与土壤有效湿润距离(包括水平距离、垂直向上距离和垂直向下距离，下同)之间呈显著的对数关系(p<0.001)，决定系数均达到0.99以上，拟合关系极好。整体上，有效湿润距离随灌水器饱和导水率的增大呈现先快速增加后缓慢增加趋势，且有效湿润距离在灌水器饱和导水率小于0.001 4 cm/h时，距离的斜率变化随灌水器饱和导水率变化较为显著。

另外，通过模拟不同供水水头(-10～-0.1 kPa)条件下的土壤有效湿润特征可以发现(图5)，土壤有效湿润距离随负压水头绝对值的增大而减小，二者之间呈显著的指数关系(p<0.001)，决定系数达到0.98以上。整体上，负压水头绝对值与有效湿润距离之间的决定系数略小于灌水器饱和导水率与有效湿润距离之间的值。

2.2.2不同组合情景负压微润灌土壤有效湿润体特征情景模拟

由模拟结果可得，不同灌水器饱和导水率、供水水头及灌水器埋深组合情景下的土壤湿润体主要呈现3种典型湿润体形式(A、B、C型，图6)，且其明显折线处所对应的土层位置也有所差异，可能是由于不同灌水器埋深对应的临界土层及其上下土层的土壤容重差异所导致的。进一步分析发现A型湿润体主要出现在浅层灌水器埋深和高压力水头条件下，即包括灌水器埋深为5 cm时的所有供水水头以及灌水器埋深为10 cm的高压力水头(-2 kPa)所形成的湿润体。通常情况下，A型湿润体的主要特点为垂直湿润距离较短(0～20 cm)，但由于其在地表的湿润范围较大，往往导致地表蒸散发量大、土壤水分利用效率低。B型湿润体一般出现在灌水器中等埋深(10～15 cm)和高灌水器饱和导水率条件下，其主要特点是垂向湿润距离较A型更大(0～30 cm)，最大水平湿润距离出现在灌水器所在位置的同一水平面上，地表湿润范围较A型较小，造成地表蒸发少、土壤水分利用效率较A型略强。C型湿润体主要出现在中等灌水器埋深(10～15 cm)和高灌水器饱和导水率条件下、以及深层灌水器埋深(20 cm)的所有的灌水器饱和导水率条件下，其最大垂直湿润距离(0～35 cm)较A型和B型湿润体有所增大，而地表湿润范围则有所减小，甚至不产生地表湿润，因此，其地表蒸发损失最低，节水效果最好。

2.2.3基于HYDRUS-2D的典型设施作物负压微润灌技术参数筛选

结合HYDRUS-2D模型对负压微润灌不同灌水器参数组合下的土壤湿润体模拟结果，选择6种灌水器饱和导水率参数(0.000 2、0.000 4、0.000 8、0.001 4、0.002、0.004 cm/h)、5种供水压力水头(-2、-4、-6、-8、-10 kPa)和4种灌水器埋深(5、10、15、20 cm)进行组合，借助反演模型模拟了120种情景组合下土壤湿润体特征。根据典型设施作物根系分布特征(表5)，以土壤湿润体的湿润距离与根系分布层的匹配情况以及生产实践中作物对根区水分的正常需求为判断依据，确定了不同根系设施作物适宜的负压微润灌湿润体特征类型及其对应的技术参数范围(表6)。

从表2中可以看出，每组数据中所包含的粗差数量并不多，对平均值的影响比较微弱，各组数据的数量不同是因为实际观测时间长短不同，同一距离处的一组数据可以看作重复性观测。

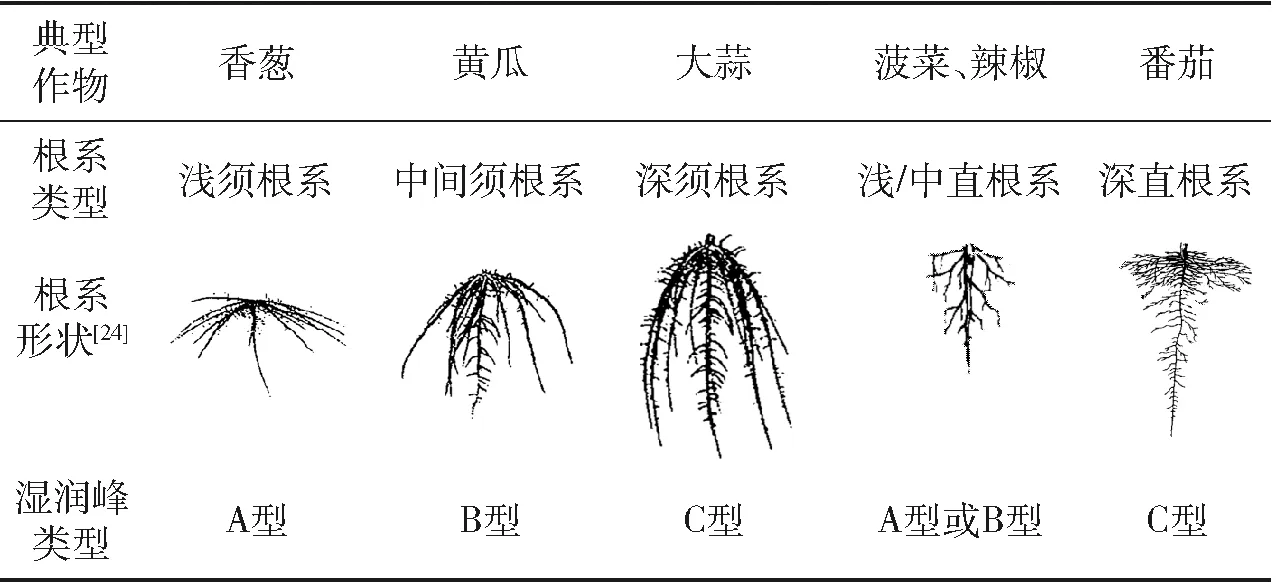
表5 典型设施作物根系形状和灌溉组合

由表5可以看出，浅须根系作物由于其主要根系分布层较浅、水平根系较宽，因此与A型湿润体较为匹配。中间须根系作物由于其主要根系在土壤中层位置的分布较宽，根系垂向范围略大于水平方向范围，因此与B型湿润体较为匹配。深须根系和深直根系由于其根系在垂向的分布显著大于水平方向的分布，因此与C型湿润体更为匹配。浅直根系由于其存在根系主要分布层较浅、垂向分布显著大于水平分布等特点，因此与A型或B型均较为匹配。

此外，进一步分析不同设施作物的负压微润灌技术参数推荐范围(表6)可以看出，由于香葱和菠菜的根系分别属于浅须根系和浅直根系，所以符合A型湿润体对应的负压微润灌技术参数范围，即灌水器饱和导水率主要维持在0.000 2～0.002 cm/h范围内，供水水头和灌水器埋深范围分别为-8～-4 kPa和0～5 cm。与香葱和菠菜相比，黄瓜和辣椒的根系属于中间须根系或者中直根系，所以符合B型湿润体对应的负压微润灌技术参数范围，因此其供水水头和灌水器埋深主要维持在-6～-2 kPa和5～10 cm范围内，但考虑到黄瓜的根系水平和垂直分布范围略小于辣椒，因此其灌水器饱和导水率(0.000 4～0.000 8 cm/h)较辣椒(0.001 4～0.002 cm/h)有所减小。对于番茄、大蒜来说，由于其根系垂向深度和水平宽度主要维持在20 cm以上，因此可参考C型湿润体对应的负压微润灌技术参数范围，结合情景参数的设置和模拟结果分析发现，其灌水器饱和导水率和供水水头相对固定，分别为0.001 4～0.004 cm/h和-4～-2 kPa，灌水器埋深为15～20 cm。

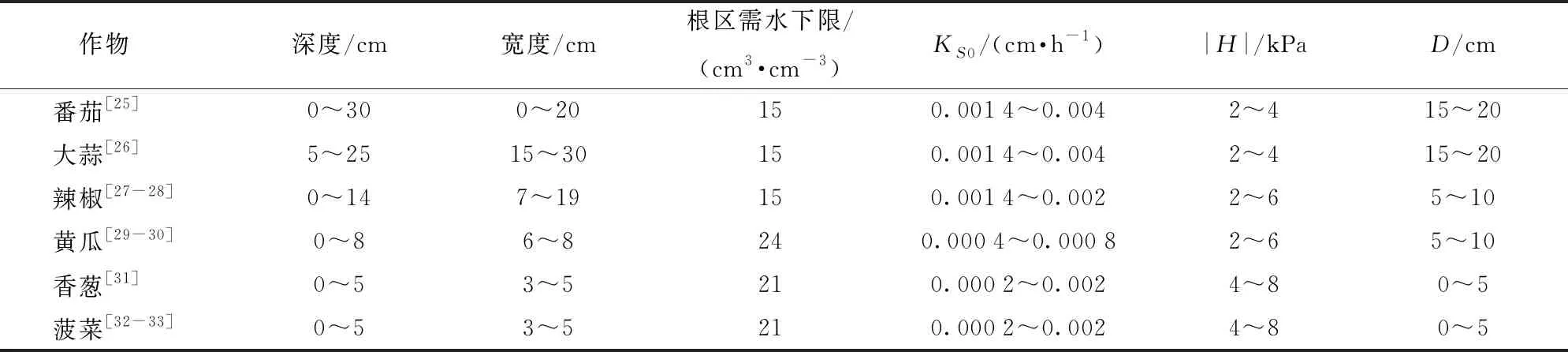
表6 作物根系分布、生长需水量及其负压微润灌技术参数推荐范围

2.3 讨论

土壤水力特征参数的精确与否决定了模型模拟结果的可靠性。关于土壤水力特征参数及其对模型模拟精度的评价等方面的研究，国内外相关学者已经通过多种方法开展了部分研究工作。例如，ZHANG等[18]通过研究预测模块、实测土壤持水曲线及模型反演3种方法计算的土壤水力特征参数对模拟结果的可靠性，结果表明采用反演模块计算的土壤水力特征参数值的模拟结果精确最高，且反演后的土壤饱和导水率KS变化最为明显，即0～21.5 cm和21.5～70 cm土层的KS分别由35.31、34.88 cm/d增加到176.9、50.72 cm/d。本研究结果表明，基于HYDRUS-2D模型反演模块计算的土壤水力特征参数能够较好地模拟负压微润灌不同供水水头条件下的土壤湿润体特征，且由模型预测(RETC)模块和反演模块计算的土壤饱和导水率KS之间也存在较大差异，这一结果与文献[18]较为相似。此外，本研究还发现，基于实测数据和模型反演得到的土壤0～16.5 cm和16.5～45.0 cm土层的KS分别为0.012、0.008 cm/h，与文献[18]中KS结果存在显著差异，这一现象可能是由土壤质地的差异所导致。例如，WANG等[8]基于实测土壤水力特征曲线计算得到壤土的KS为0.011 cm/h；毛乾屹等[34]基于HYDRUS-2D模型率定的砂壤土、壤土和砂土的土壤KS分别为63.01、24.04、81.52 cm/d。

灌溉技术的创新与发展推动了现代农业的进步，基于模型模拟的土壤水分入渗过程能够较好地阐述负压微润灌土壤水分运动特征。以往关于负压微润灌的文献主要基于土箱试验和模型模拟研究了不同供水水头、灌水器埋深对土壤水分迁移特征及作物生长产量的影响[10]，未能将负压微润灌土壤湿润体特征与实际生产中作物根系分布特征及根区需水规律进行有效衔接。且受灌水器参数、供水水头以及土壤质地等因素的影响，在实际应用过程中仍缺乏较为完整的负压微润灌技术参数选择标准，限制了其更广泛的应用。本研究以土壤湿润体有效湿润距离为目标，以土壤湿润体与作物根系匹配情况以及作物根系对水分的需求为筛选依据，确定了典型设施作物适宜的负压微润灌技术参数范围，研究结果对于生产实践过程不同作物负压微润灌参数的选择以及负压微润灌技术的大面积推广应用提供了技术指导。然而，考虑到负压微润灌土壤湿润体的左右对称性，本研究中仅针对右半个陶土灌水器及其在右侧土体的土壤水分入渗过程进行了模拟，且重点研究了以供水水头为变量因子的土壤水分运移特征，考虑到模型模拟过程中仅需考虑的土壤水吸力作用(土壤基质势差值产生)对模型相关参数和模拟结果无较大影响，因此，本研究中确定的负压微润灌技术参数(灌水器饱和导水率、供水水头和灌水器埋深)在由半柱体向全柱体推广过程中具有较好的适用性。然而，若在推广过程中涉及到累积灌水量等参数，其全柱体下的实际灌水量应为基于半柱体模拟灌水量结果的2倍。

此外，在模拟过程中还发现，土壤湿润体垂直向下的湿润距离小于垂直向上和水平方向的湿润距离，这一结果与范严伟等[35]研究发现的土壤湿润体垂直向上距离小于水平距离和垂直向下距离等结果并不一致。分析其原因可能为，本研究中0～16.5 cm和16.5～45.0 cm土层的土壤容重分别为1.25、1.35 g/cm3，下层较高的土壤容重减小了土壤颗粒间孔隙，限制了土壤水分的迁移过程，导致该现象产生[17]。上述结果意味着分层容重可调控湿润体在不同方向的有效湿润距离，为今后的负压微润灌发展提供新的研究方向。

3 结论

(1)基于负压微润灌不同供水水头(-2、-4、-6 kPa)处理下的土壤水分特征(土壤含水率、累积水分入渗量和湿润距离)实测值为依据，对HYDRUS-2D模型进行了反演与验证，构建了适用于负压微润灌条件下的HYDRUS-2D模型，验证结果表明该模型能够较好地模拟负压微润灌不同供水水头条件下土壤含水率、累积入渗量和湿润距离(水平和垂直方向)的同步变化规律。

(2)基于反演模型对不同灌水器饱和导水率和负压微润灌供水水头条件下的湿润距离模拟结果表明，灌水器饱和导水率和供水水头与土壤湿润距离分别呈对数和导数关系，且其决定系数均达到0.98以上，相关性均达到极显著水平。

(3)基于反演模型对负压微润灌120种技术参数组合(不同灌水器饱和导水率、供水水头以及灌水器埋深)情景的土壤水分模拟结果，并结合常见设施作物根系分布及其根区需水特征，确定了不同设施作物适宜的负压微润灌技术参数范围。