基于SPSS的山前侧向补给量与降水量、地下水埋深的相关性研究

李民诗，白国营

北京市水文总站，北京 100089

北京是严重缺水的城市之一，并且自1999年连续干旱以来，地表水资源锐减，因此地下水在北京市供水中具有重要的作用。但是，长期开采地下水和引入南水北调水，改变了地下水动态、赋存及流场等条件的原有状态和格局，对水资源量中的山前侧向补给量产生了一定的影响。

常规计算山前侧向补给量的方法为达西定律法，但在实际操作中，对于断面的划定，各含水层的渗透系数选取、水力梯度的确定均存在一定困难，导致真实值与实际值存在一定偏差。因此，通过探讨北京山区降水量、地下水埋深、山前侧向补给量之间的相关性，有助于计算山前侧向补给量。

1 研究区域概况

1.1 自然地理条件

北京市位于华北平原的北缘，大部分地区均与河北省毗邻，东南部与天津市接壤，西、北、东北三面环山，东南方向为平原。北京行政区划分为16个区，全市面积约16410km2，其中平原区面积为6900km2（包括延庆盆地）；地理坐标为东经115°25´～117°30´，北纬39°28´～41° 05´。

北京市地形西北高，东南低。西部为太行山脉，北部为燕山山脉，山区多属中低山地形，东南是缓缓向渤海倾斜的平原，其平原形状很像一个群山丛中突入渤海的海湾，故有“北京湾”之称。

1.2 水文地质条件

北京西部的西山和北部的燕山山区与平原区交界，主要由砂砾岩、碳酸盐岩、页岩等组成。山区基岩与第四系砂卵砾石直接接触，平原区第四系孔隙水系统直接接受大量的山区基岩裂隙水系统和山前岩溶水系统地下水的侧向径流补给，并且在局部地带接受山前岩溶水系统中隐伏岩溶水的越流补给。

根据选定剖面上钻孔抽水试验或经验数值确定的含水层Kcp值，怀柔、密云砂卵砾石层Kcp值最大可达300m/d，昌平砂夹黏土碎石Kcp值最小仅为4m/d。山前地带径流条件较好，水力坡度在2.76‰～4.15‰；冲洪积扇顶部向中部含水层水力坡度呈减小趋势，径流变弱，水力坡度为0.50‰～1.29‰；冲洪积扇下部地下水径流条件变差，水力坡度为0.25‰～1.00‰。

2 山前侧向补给量研究方法

目前，研究地下水的统计方法较多，包括多元线性回归、BP神经网络、时间序列等。根据实际情况，此次选用SPSS统计分析软件，建立多元回归模型，研究北京市山区侧向补给量。

2.1 方法介绍

回归分析法可以在掌握一定量观测数据的前提下,用数理统计的方法建立自变量与因变量之间的回归函数关系。回归分析根据自变量的数量可分为一元回归分析和多元回归分析；按照表达式的不同形式可分为非线性回归分析和线性回归分析。通常一种现象与多个因素相联系，由多个自变量的最优组合共同预测或估计因变量，更符合实际。

多元线性回归模型的因变量与自变量之间为线性关系，其数学模型为

Y=β0+β1X1+β2X2+…+βpXp+ε

式中：Y为因变量；Xj为自变量，j=1，2，3，…，p；β0为常数项；β1～βp为未知回归系数，为随机变量。

2.2 回归方程的检验

（1）F检验。对多元线性回归方程的显著性检验一般采用F检验法，其统计量如下：

式中：SSR为回归平方和；SSE为残差平方和。

当F≤Fa（n-p-1）时，认为回归方程不显著；当F＞Fa（n-p-1）时，回归方程是显著的。

（2）拟合优度检验。用拟合优度检验回归方程对样本预测值的拟合程度。在多元线性回归方程中，定义样本确定性系数为

式中：SST为总离差平方和。

（3）t检验。在多元线性回归方程中，需要对自变量进行显著性检验分析，零假设为βj=0，即第j个回归系数为零，对应的自变量对因变量y的作用不显著。零假设成立时，构造统计量t如下：

t服从自由度（n-p-1）为t分布。给定显著性水平α，当时，模型线性效果不显著；当时，模型线性效果显著。

与F检验相比，R2能更直观地反映回归拟合的效果，但不作为严格的显著性检验。

上述3种检验可以鉴定回归模型与实际情况拟合效果是否良好，因此只有建立的模型能够满足3种检验时，才可认定模型具有一定的实用价值。

3 多元线性回归模型的建立

3.1 数据来源

对2005年—2017年山区年降水量、地下水埋深、山前侧向补给量数据进行多元线性回归分析，分析数据采用《北京市水资源公报》所统计的数据。2005年—2017年山前侧向补给量与山区降水量、地下水埋深统计表如表1所示。山前侧向补给与地下水埋深和山区降水量的关系如图1、图2所示。

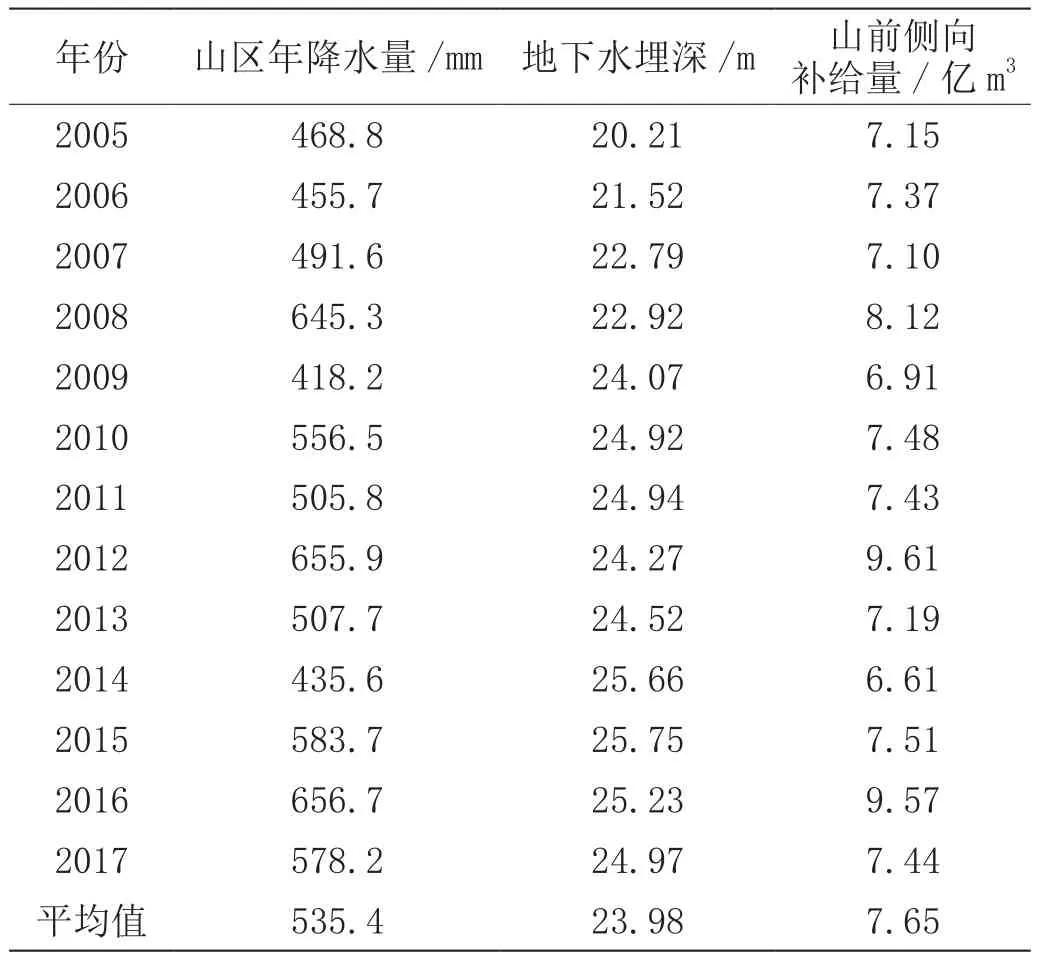
表1 2005年—2017年山前侧向补给量与山区降水量、地下水埋深统计表

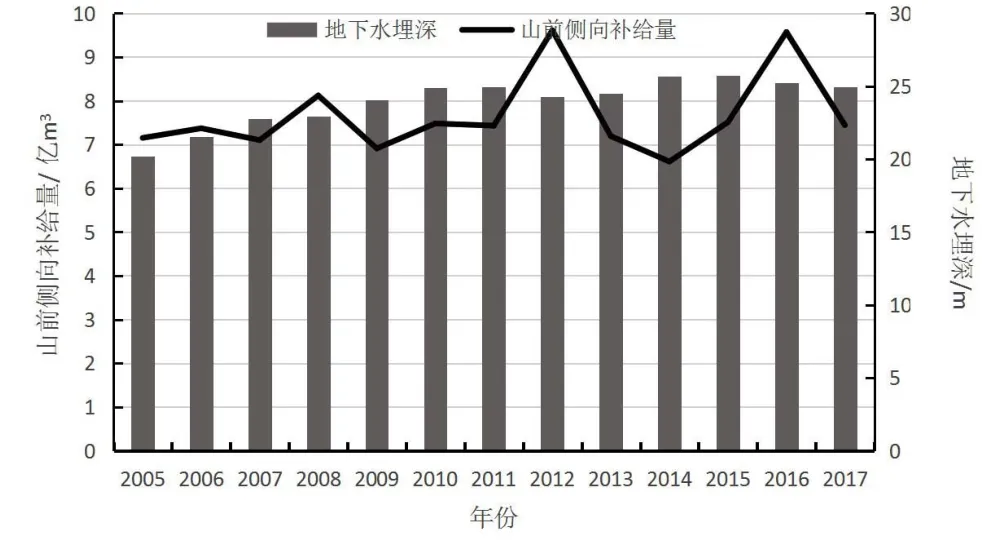
图1 山前侧向补给与地下水埋深关系图

图2 山前侧向补给与山区降水关系图

由图1、图2可知，山前侧向流出量与山区降水量及地下水埋深存在一定的关联性，通过统计模型进行验证。

3.2 多元回归模型

模型选用侧向流出量Qt作为因变量，地下水埋深Dt、降水量Pt作为自变量，利用SPSS软件建立多元回归模型，可得回归模型方程如下：

模型检验结果显示，决定系数R2=0.729，方程拟合度可以。同时，对数据进行残差分析可知，模型中所用数据残差符合正态分布，无强影响值出现。

3.3 模拟数据与原始数据对比

将模拟数据与原始数据进行对比，进一步验证多元线性回归模型的可靠性，如表2和图3所示。

图3 年山前侧向补给量原始数据与模拟数据对比图

表2 年山前侧向补给量原始数据与模拟数据对比表

由表2和图3可知，除了2008年，其他年份模拟数据与原始数据误差均＜10%，整体趋势一致，可知该模型在分析山区年降水量、地下水埋深、山前侧向补给量相关性方面具有一定的利用价值。

4 结论

（1）文章通过SPSS软件建立关于山区年降水量、平原区地下水埋深、山前侧向补给量的多元线性回归模型，模拟结果与实际数据基本一致，模型具有一定实用性。

（2）通过分析，建立了山区年降水量、平原区地下水埋深、山前侧向补给量的相关模型，Qt= -0.061Dt+ 0.01Pt+3.886，为山前侧向补给量的计算提供了新的途径。