一种面向工控系统的PU学习入侵检测方法
2021-08-25吕思才张耀方刘红日王子博王佰玲
吕思才,张 格,张耀方,刘红日,王子博,王佰玲*
1计算机科学与技术学院 哈尔滨工业大学(威海) 威海 中国 264209
2国家工业信息安全发展研究中心 北京 中国 100040
3网络空间安全研究院 哈尔滨工业大学 威海 中国 264209
1 引言
工业控制系统(Industrial Control System)是用于工业生产的控制系统,是国家基础设施的重要组成部分,被广泛应用到水利、核电和能源等关键领域中,作为国家基础设施的核心控制设备,其安全关系国计民生[1]。
随着工业控制系统的迅速发展,在其被广泛应用的同时,安全事件也开始频发。2010年,“震网”(Stuxnet)病毒爆发,直接导致伊朗核设施的离心机大面积损毁,震网病毒爆发之后,工控系统开始逐渐成为攻击者的主要攻击目标之一[2]; 2017年,全球爆发的WannaCry 勒索病毒借助高危漏洞“永恒之蓝”(Eternal Bule)在世界范围内爆发,影响多国能源、交通、通信等重点行业[3]; 2018年3月,美国计算机应急准备小组发布了一则安全通告 TA18-074A,详细描述了俄罗斯黑客针对美国某发电厂的网络攻击事件。该攻击以收集情报为目的,向计算机植入程序记录有关信息进行攻击,对发电厂造成巨大损失[4]。2019年,委内瑞拉最大的电力设施古里水电站计算机系统控制中枢遭受到网络攻击,引发全国性大面积停电,约3000万人口受到影响; 同年7月,委内瑞拉古里水电站再次遭到攻击,导致包括委内瑞拉首都加拉加斯在内的16个州发生大范围停电[5]。正是由于工业控制系统是国家基础设施的重要组成部分,因此针对工业控制系统的攻击通常会造成更严重的后果,更巨大的经济损失。
针对工业控制系统受到的安全威胁,使用入侵检测手段进行防护是一项重要手段。目前基于工业控制系统的入侵检测展开了多方面的研究,通过结合机器学习模型实现对工业控制系统入侵的智能化检测。在多样的机器学习模型中,OCSVM模型在训练数据上只需要一类数据,这使得其可以发现未知的入侵,因此成为工业控制系统入侵检测的常用方法。然而由于反例训练数据的缺失会使得训练的模型具有较高的 FPR(False Positive Rate,假阳性率),因此本文引入PU学习模型来进行入侵检测,将正常流量作为正例标签数据训练模型,保留模型对于未知入侵的检测能力的同时,提升模型对于入侵的检测能力。而PU学习模型同时将一类标签数据和待检测的无标签数据用于模型的训练,因此PU学习模型的分类性能往往高于异常检测模型。
本文的主要贡献可以概括如下:
(1) 针对工业控制系统数据维数高、关联性强的特点,本文提出一种基于PU学习的特征重要度计算方法,该方法可以基于正例标签数据和无标签数据计算出特征的重要度,以用于特征选择。
(2) 在 PU 学习的类先验概率估计上,本文分析了基于正例标签频率的类先验概率估计算法,并通过OCSVM模型划分可信赖的正例子集,改良了正例标签频率的计算方法,减小了先验概率估计的误差。
(3) 基于工业控制系统攻击的隐蔽性特点,将PU学习应用到工业控制系统入侵检测,构建神经网络进行PU学习,在仅有正常流量作为标签数据的情况下训练分类模型,并通过公开数据集实验进行实验验证模型的有效性。
本文的结构如下: 第 2节介绍工业控制系统入侵检测和PU学习的研究现状; 第3节为本文的主要研究内容; 第 4节通过实验验证提出的算法的有效性; 第5节对文章进行总结。
2 相关工作
2.1 工业控制系统概述
工控网络层次模型从上到下共分为 5个层级,依次为企业资源层、生产管理层、过程监控层、现场控制层和现场设备层,不同层级的实时性要求不同。企业资源层主要包括 ERP系统功能单元,用于为企业决策层员工提供决策运行手段,如图1所示。
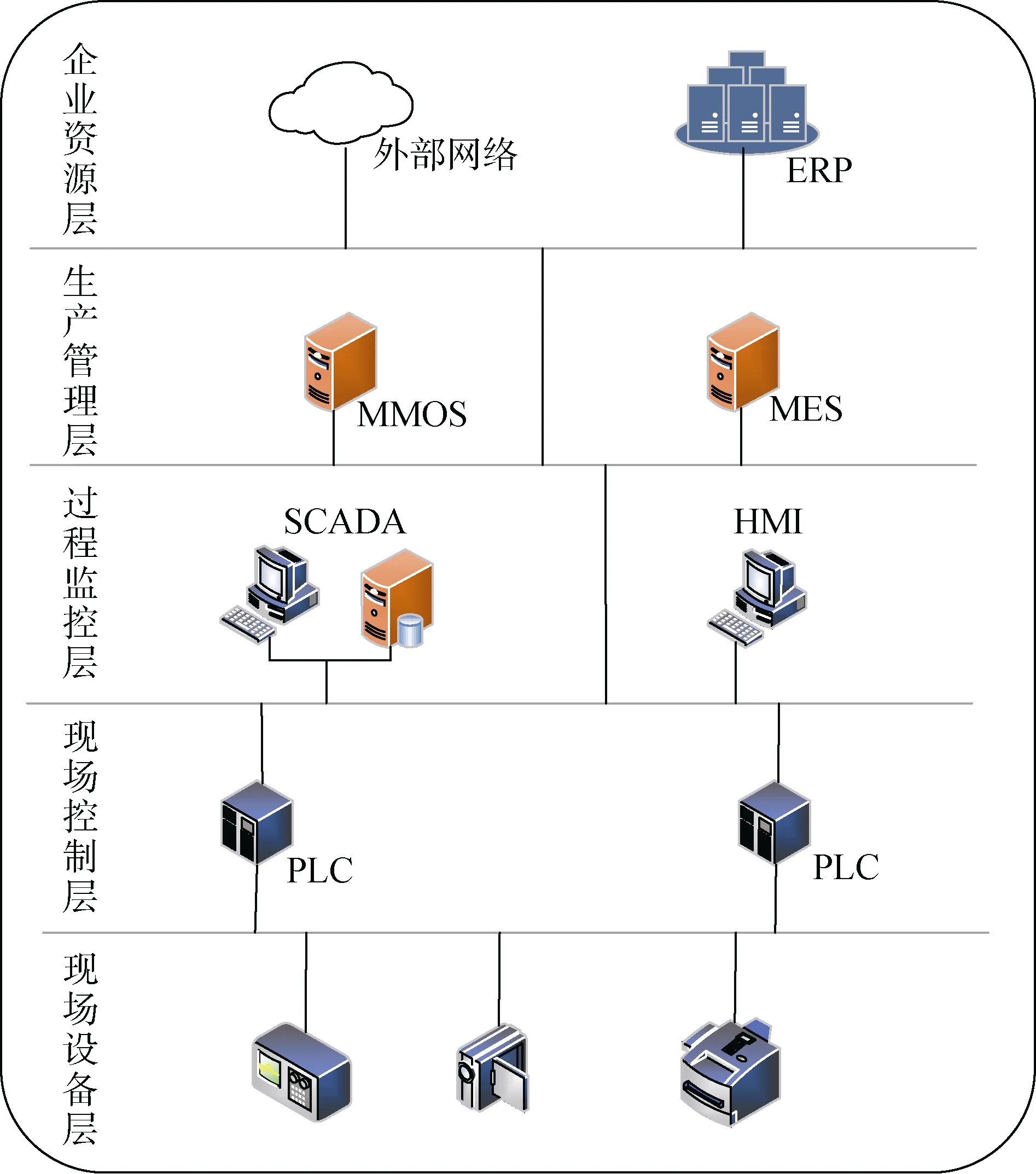
图1 工业控制系统层次结构Figure 1 Architecture of an Industrial Control System
工业控制最底层是现场设备层,其包含一些应用在现场的设备,如传感器,监控器等一些执行设备单元,用于对生产过程进行感知与操作。
过程监控层和现场控制层是用于监视和控制现场设备。其中过程监控层主要包含SCADA和HMI,SCADA可以对现场的运行设备进行监视和控制,以实现数据采集、设备控制、测量、参数调节以及各类信号报警等各项功能; HMI为人机界面,用于系统和用户之间进行信息交互。现场控制层主要是PLC,PLC向上与 HMI相连,接收控制命令和查询请求,向下与现场设备相连,通过发送操作指令对现场设备进行控制。
生产管理层中包含MES和MOMS,用于对生产过程进行管理,如制造数据管理、生产调度管理等。
最上层为企业资源层,企业资源规划(ERP)系统管理核心业务流程,如生产或产品计划,物料管理和财务情况等。
2.2 工业控制系统入侵检测特点
工业控制系统的入侵检测与互联网的入侵检测存在显著差别,由于工业控制系统的环境的特殊性,其具有独特的特征[6]:
(1) 高实时性。工业控制系统通常部署在电力、核能等领域中,系统具有较高的实时性,因此也要求入侵检测具有较高的实时性。
(2) 工控设备资源受限。工业控制系统包含大量执行特定操作的传感器和执行器,为降低成本,其拥有的计算、存储资源通常十分有限。
(3) 设备难以更新,重启。工业控制系统与物理世界联系紧密,通常无法暂停工作,否则会对整个工业控制系统、人员、环境造成严重的危害。
基于以上工业控制系统的特征,实际上对入侵检测系统就提出的较高的要求:
(1) 实时性。工业控制系统对入侵检测具有更高的实时性要求,要求入侵检测系统可以利用工业控制系统的实时信息进行入侵检测。
(2) 资源受限。工业控制系统资源受限的特点对入侵检测的方法进行了限制,要求入侵检测模型具有较低的资源消耗。一些基于深度学习的算法的时间复杂度就相对较高,特别是深度学习模型,抛开训练时间不谈,一些深层的神经网络模型,其网络结构复杂参数量非常大,所需的训练和预测时间也较长。在资源首先的情况下,一些复杂的深层神经网络模型难以适用于工业控制系统的入侵检测。因此在将神经网络模型运用到工业控制系统的入侵检测是,需要着重考虑模型的复杂度,在保证准确率的同时尽可能使神经网络结构简单。
(3) 设备难以更新和重启。这一特点对入侵检测模型性能进行了限制。首先由于设备难以更新模型需要具有较好的泛化性能,即在训练数据上训练的模型运用到真实数据上同样需要具有较好的性能;其次是指标的要求,由于设备无法重启或暂停,因此进行入侵检测需要具有较高的查准率,即宁可漏报也不误报。
以上是工业控制系统的特点,在进行入侵检测时,通常需要基于其流量进行分析,工业数据的特点是维数高、关联性强,这会增加入侵检测模型的训练时间,因此需要对工业数据特征提取,降低后续数据建模和处理的复杂度[15]。
基于工业控制系统高查准率,低资源消耗的要求,以及其数据标签难获取的特点,本文构建浅层神经网络进行 PU学习,用于工业控制系统入侵检测。同时针对工业控制系统数据维度高,关联性强的特点,提出一种基于PU学习的特征选择算法用于数据降维。
2.3 工业控制系统入侵检测相关工作
工业控制系统入侵检测按照检测的数据可以分为: 基于流量的检测,基于设备状态的检测和基于协议的检测。在流量上,通过工业控制系统真实流量构建特征,如流持续时间,端口等信息,然后结合一些机器学习模型进行检测,如 OCSVM[7]; 在设备状态上,魏战红等人提出一种基于 CUSUM 算法的入侵检测方法,在该方法中首先以传感器获取的实际值和模型预测值之间的差值作为统计序列,根据3σ原则设计偏移常数决定阈值,最后在实验中验证了该方法可以有效检测偏差攻击和几何攻击; 在协议上,一些工控协议是公开的,可以依据这些协议的规范制定检测规则,对特定工控协议进行检测,如Modbus协议[8-9]。
随着机器学习和人工智能的迅速发展,其影响逐渐辐射到入侵检测领域,大量机器学习模型被用于入侵检测,按照适用的机器学习算法不同,可以分为传统分类模型,聚类模型[10-11],集成模型,异常检测模型和神经网络四类。由于神经网络发展迅速,且表现出了比传统机器学习模型更好的分类性能,因此,基于传统分类模型的入侵检测逐渐降温。集成模型和异常检测模型各有特点,集成模型由多个基分类器集成分类性能较好,且如随机森林[12]; 异常检测如 OCSVM 的优点有: 1) 对于未知的入侵具有检测能力; 2) 仅需要背景流量作为训练数据。随着研究的深入,自编码器等神经网络被用于无监督的异常检测[13]。
入侵检测最常用的异常检测算法是OCSVM,李琳等人[14]调研了 OCSVM 算法在工业控制系统入侵检测中的应用。在网络层和传输层上,OCSVM算法被用于SCADA系统的TCP/IP流量异常检测; 在应用层上,基于 ModbusTCP正常通信流量训练OCSVM 模型进行入侵检测。同时文中也指出了OCSVM异常检测存在三个主要问题: 工业控制系统的特征构建问题,参数寻优问题和较高的误报率。
随着深度学习的推广,大量深度学习模型被用于入侵检测,包括: RNN(Recurrent Neural Network,循环神经网络),CNN(Convolutional Neural Networks,卷积神经网络),DBN (Deep Belief Network,深度信念网络),AE(AutoEncoder Network,自编码网络)。深度学习模型相较于 OCSVM 等经典的异常检测模型,在检测率上有了提升,但是训练模型所需的时间也更长。
表1中总结了近几年的基于机器学习的工业控制系统入侵检测相关工作,从相关工作分析,工业控制系统的入侵检测研究具有如下趋势:

表1 机器学习在工业控制系统入侵检测中的应用Table 1 Summary of work related to intrusion detection
(1) 趋向于异常检测。工业控制系统的入侵检测更多的是被作为异常检测问题处理,在模型选择上偏好OCSVM等一分类模型或AE等无监督模型进行识别。
(2) 趋向于高精度。在进几年的研究工作中部分研究者趋向于通过一些参数优化算法如粒子群算法(PSO)和引力搜索算法(GSA)优化模型参数,使模型具有更好的分类性能。
(3) 趋向于实时高效。工业控制系统由于资源受限,因此要求模型具有较小的计算成本,从相关工作来看,工业控制系统入侵检测更加注重低计算消耗的模型,同时大多在训练模型前通过特征选择或特征提取的方法,如PCA,fisher分值进行降维,从而减少模型训练所用的时间和计算量。
2.4 PU学习
PU学习可以视为一种基于神经网络进行异常检
测的方法,其通过正例数据集和无标签数据集来估计二分类误差,从而使PU学习模型可以达到接近二分类模型的分类性能。
由于 PU学习需要通过正例数据集和无标签数据集训练模型,为了有效的估计二分类误差,无标签数据集在应用到 PU学习之前需要对其正例和反例样本的混合比例进行估计[31-32],也被称为类先验概率估计(class prior estimation)。类先验概率估计主要方法是从PU数据集的分布着手,由于无标签数据集中混合了正例和反例数据,所以实际上无标签数据集的分布由正例数据分布和反例数据分布组合而成,通过比较PU数据集的分布可以求出类先验概率[33-35]。除此以外,基于正例标签频率的类先验概率估计算法是目前最为先进的算法之一,Jessa Bekker等人[36]提出TIcE算法,通过在无标签数据集中划分可信赖的正例子集来估计正例标签频率,这也是目前时间复杂度最低的算法。
2014年,Plessis等人[37]首先对PU学习问题进行了理论分析,将PU学习与二分类模型进行比较,在已知类先验概率π的条件下估算出二分类样本的损失,理论上其可以获得和二分类模型相同的决策面,该模型被称为uPU(unbiased Positve-unlabeled learning)。针对 uPU模型损失函数需要满足对称条件,Plessis等人[38]继续展开研究,给出了一种将不满足对称条件的损失函数应用于 uPU中的方法,并验证了非凸损失函数和凸损失函数具有相似的精度。2016年,Plessis等人[39]进一步比较了PU学习模型与二分类模型,分析了在一些情况下PU学习模型性能比二分类模型更佳的原因。
2017年,Ryuichi Kiryo等人[40]针对uPU容易发生过拟合的问题,提出了 nnPU(Positive-unlabeled learning with Non-negative risk estimator)算法,在uPU的基础上,对其估计二分类损失的方法进行改进,保证了估计的反例损失恒为正数,从而避免了由于估计的损失为负数带来的问题,并指出nnPU性能优于uPU。最后,Jessa Bekker等人[41]对现有的PU学习进行了总结,在文章中针对目前PU学习的七个主要问题进行了分析,其中包括PU学习的假设,评价指标,主要模型和类先验概率估计等。
3 基于PU学习的入侵检测
工业控制系统的入侵检测问题被作为异常检测问题收到学者们的关注,但是一些经典的异常检测算法如OCSVM算法,具有较高的误报率,分类性能同二分类模型相比具有较大差距。本文提出使用PU学习进行入侵检测,该方法被证明具有接近二分类的分类性能,同时在训练数据上同 OCSVM 模型一样只需要一类标签数据。
基于PU学习的入侵检测流程如图2所示,在特征工程上,需要通过正例标签数据和误标签数据对特征进行分析,选择关键特征,降低数据维度,减小无关特征对模型分类性能的影响; 同时PU学习的类先验概率作为先验知识,需要在进行特征工程的同时进行处理,通过分析正例数据和误标签数据,构建模型,估计误标签数据集的类先验概率; 然后结合特征选择后的正例标签数据、无标签数据以及类先验概率,训练PU学习模型,最后输出模型和误标签数据集的分类标签。
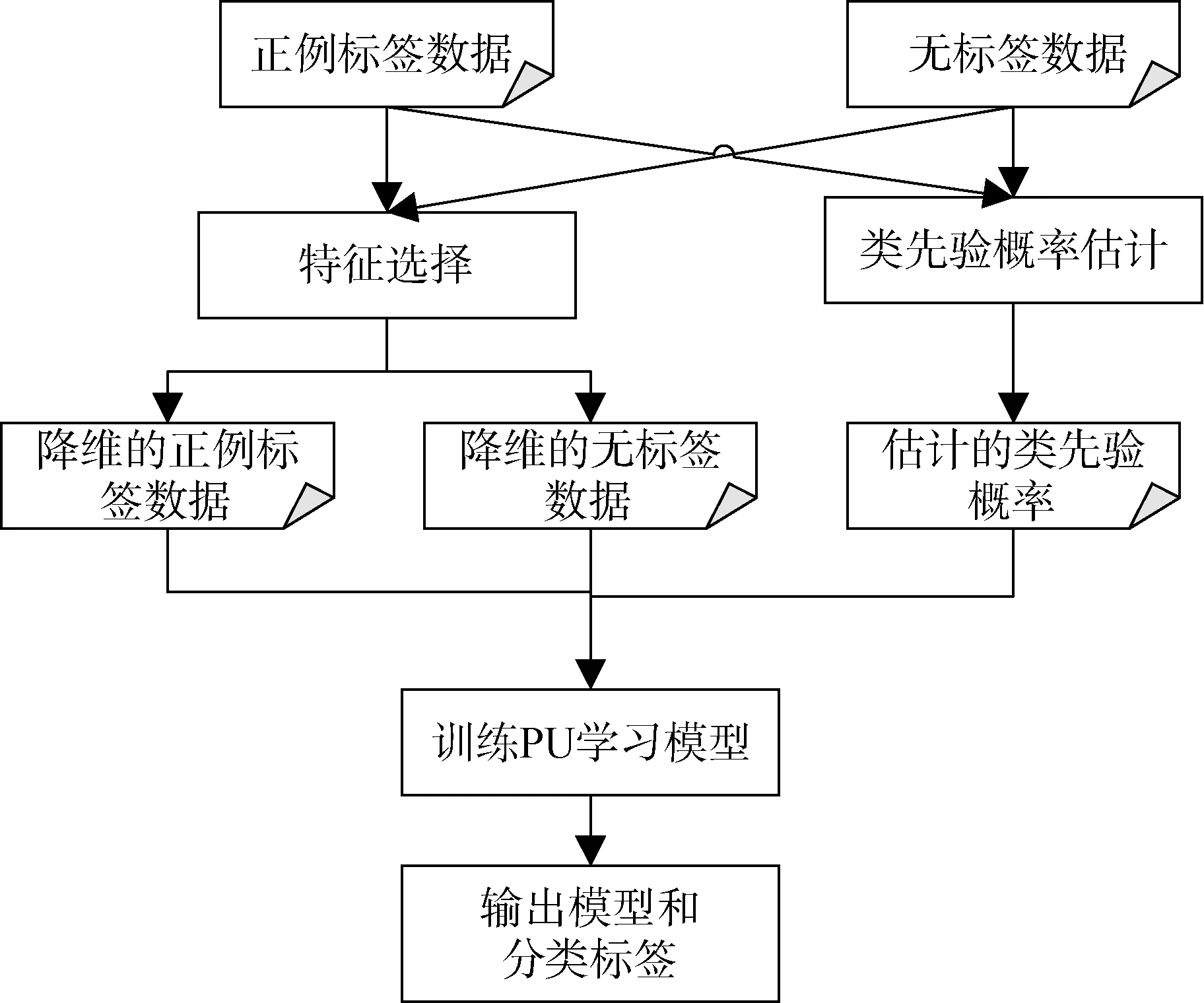
图2 基于PU学习的入侵检测流程示意图Figure 2 Schematic diagram of intrusion detection process based on PU learning
基于以上流程,本部分主要的研究内容分为三部分: 首先,探索一种基于PU学习的特征选择算法,基于正例标签数据和无标签数据分析特征的重要度;其次,研究类先验概率估计算法,提升类先验概率估计的准确度,为PU学习提供重要先验知识; 最后,基于特征选择之后的数据和估计的类先验概率,通过PU学习训练分类模型。
在本文的研究中分别对异常检测存在的问题有针对的进行了回答:
(1) 在特征工程上,本文基于 PU学习研究了特征重要度计算方法,可以作为特征选择的度量标准对工业控制系统数据进行特征选择;
(2) 在工业控制系统资源限制和实时性问题上,本文选用了浅层的神经网络,其所需的存储资源和计算资源都比较少,符合工业控制系统需求;
(3) 在误报率上,PU学习已经被验证具有接近二分类模型的分类性能,相较于无监督的异常检测模型查准率较高。
3.1 PU学习的特征重要度
在工业控制系统中,数据具有维数高、关联性强的特点。当数据维度很高时,许多机器学习问题会变得困难,这种现象被称为维数灾难。特征选择是特征工程的重要内容,其原理是在所有特征抽取关键特征,从而达到降维的目的。特征选择的方法可以分为两类: 封装式和过滤式。其中封装式的特征选择通常是择定一个基模型进行多轮训练,根据训练所得模型的分类性能逐渐筛除冗余特征; 过滤式的特征选择是通过计算特征的重要度,设定阈值筛除无关特征,并进一步通过相关性筛除冗余特征。
在PU学习中,由于只有一类带标签的样本,因此,封装式的模型难以评估模型性能,因此在本文中采用过滤式特征选择方法,其中常用的特征重要度计算方法如表1所示。
过滤式特征选择方法的重要度计算方法通过评估特征与标签的相关性来计算,认为和目标类别存在明显相关关系特征是关键特征。然而在在PU学习中,只有一类标签样本,无法直接使用二分类模型中的特征重要度计算方法,因此需要寻找一种适合于PU学习场景的特征重要度计算方法。
以此二分类的重要度计算思想为启发,本文给出一种PU学习的关键特征识别方法: 考虑到无标签数据集是正例样本和反例样本混合而得,无标签数据集中特征的属性值包含了正例取值和反例取值两部分,如果该特征与类标签强相关,那么无标签数据集中该特征的属性值在分布上应该呈现出明显的双峰或多峰特征,且不同类样本特征的分布差异较大,如图3所示; 当特征与类标签弱相关时,则正例与反例样本的特征分布相似。
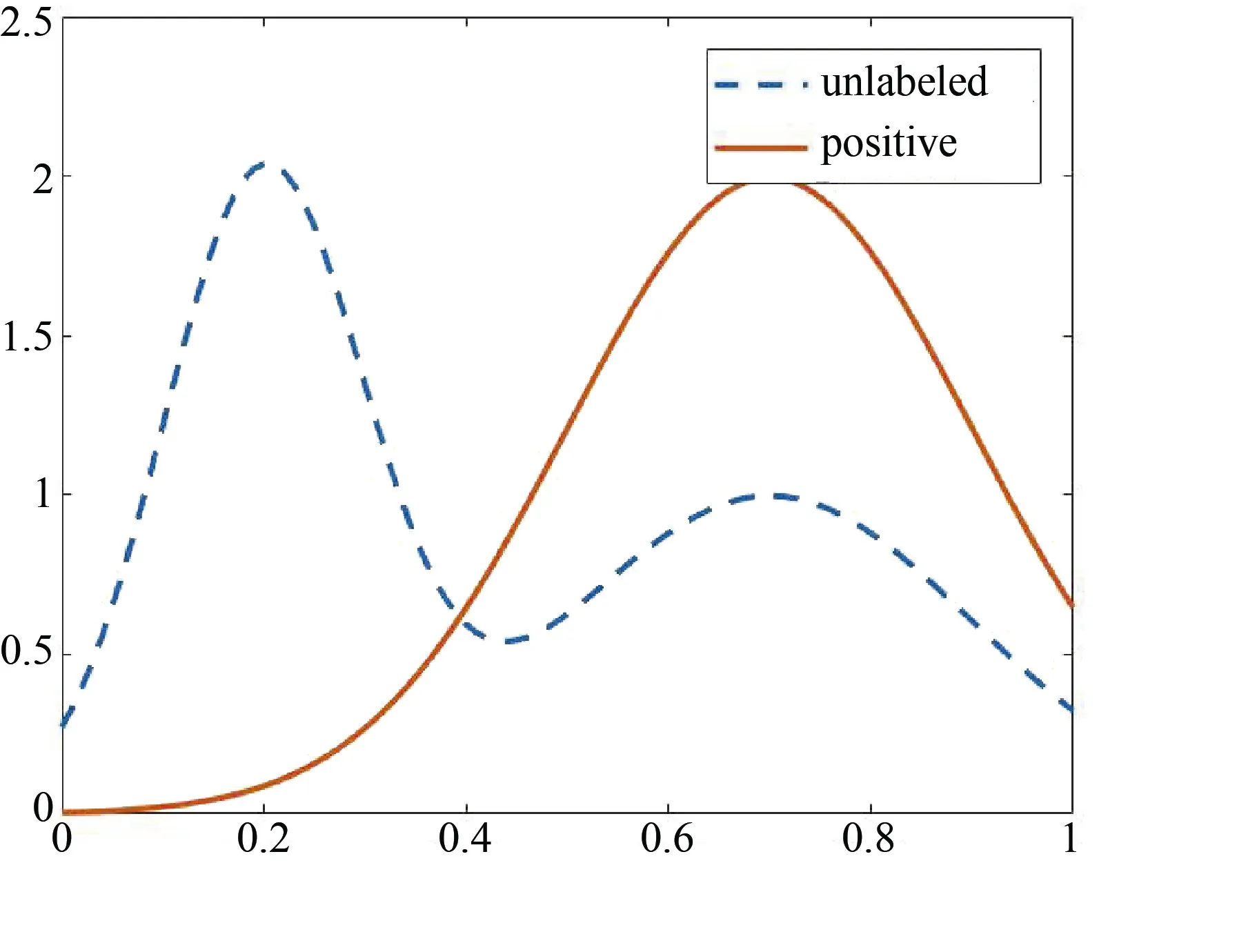
图3 PU学习的关键特征的分布Figure 3 Key feature distribution of PU learning
特征在正例数据集和无标签数据集上的分布差异即可作为特征的重要度。KL散度可以描述两个分布之间的差异,其离散形式如公式(1)所示。

KL散度在计算两个特征分布差异时,需要特征属性值的概率。首先考虑到特征的属性值取值范围没有限定,因此在计算之前需要先进行最大最小值标准化,目的是为了将标准化之后的属性值限制在[0,1]区间内; 其次,特征的属性值存在连续和离散两种形式,为了统一处理,在算法中将[0,1]区间进行等分,通过每个小区域中样本的频率作为概率计算KL散度。
算法1.基于KL散度的特征重要度算法
输入: 正例标签数据集 P,无标签数据集 U,特征重要度阈值threshold
输出: 特征选择之后的正例数据集P′和无标签数据U′
1: Initialize feature importace vectorω;
2: Load data set P and U;
3: Data normalization by MinMaxScaler;
4: FOR i=1 TO M,DO
5: Divide the [0,1]interval into 100 equal parts,and take the frequency as probability;
6: Calculate i-th featue’s importance through KL divergence: ω [i]= KLi(P||U);
7: END FOR
8: RETURN ω
时间复杂度分析: 算法中第 3步进行数据标准化,采用的数据标准化方法为最大最小值标准化,该步的时间复杂度为O(mn); 第 4~6步为计算特征重要度,通过将[0,1]区间等分,以每个小区间中的频数作为概率计算 KL散度,该部分的时间复杂度为O(m n)。因此算法的总时间复杂度为O(mn)。
通过 KL散度可以在仅有正例标签数据的场景下给出特征重要度的估计值,区分关键特征和无关特征,在不考虑冗余特征的情况下,可以基于特征重要度对特征进行过滤,如设定特征重要度阈值或指定选择的特征数。
3.2 PU学习的类先验概率估计
在工业控制系统中,大量入侵数据的采集是十分困难的,但是系统正常运行的流量和状态码的采集相对简单,以正常状态的数据作为正例标签数据,进行 PU学习是符合工业控制系统实际应用场景的,而在PU学习中,分析待检测的数据,获得类先验概率是十分重要的。PU学习的类先验概率被定义为π= p(y = 1 ),当样本的采集满足 SCAR(select at completely random)假设时,类先验概率即为无标签数据集中正例样本所占的比例。
定义 1(SCAR假设)样本的采集与样本的属性无关,是完全随机的,即:
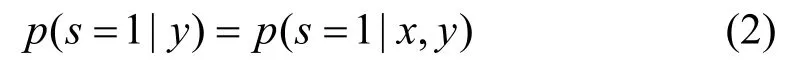
按照正例数据的来源不同可以分为两类: One Sample(OS)和 Two Sample(TS)。OS在采集数据时,仅进行一次随机采样,即在真实数据中随机采集一部分数据,在采集的数据中挖掘出一些正例数据加上标签,未标签的数据作为无标签数据; TS在采集数据时,需要进行两次采样,即首先随机采集一部分正例标签数据,无标签数据集在真实数据中通过随机抽样进行获得。
由于正例数据是通过在无标签数据集中随机选择的,因此在这种场景下产生了一个中间变量c,该变量被称为正例标签频率(label frequency),其定义为 c = p(s = 1 | y = 1 ),其中s=1表示样本被选中的样本。标签频率和类先验概率的关系可以通过公式(3)表示。

因此可以通过估计正例标签频率c,来估算类先验概率。特别地,在 TS场景下,可以将正例数据和无标签数据混合,将正例样本视为随机抽取并加上标签的正例样本,也可进行正例标签频率估计。
文献[36]中通过使用决策树来提升估计的正例标签频率的下界,从而得到正例标签频率的估计值,该算法被称为TIcE算法。本文通过OCSVM算法对TIcE算法进行改进,提出通过 OCSVM 算法来划分可信赖正例子集,进而估计正例标签频率。
OCSVM算法是一种经典的异常检测算法,当其使用RBF核函数时,性能和SVDD类似,可以认为OCSVM算法在特征空间中划分找到一个超球体,将正例样本包含在该超球体内,并且使得该超球体半径最小。其问题描述如公式所示。
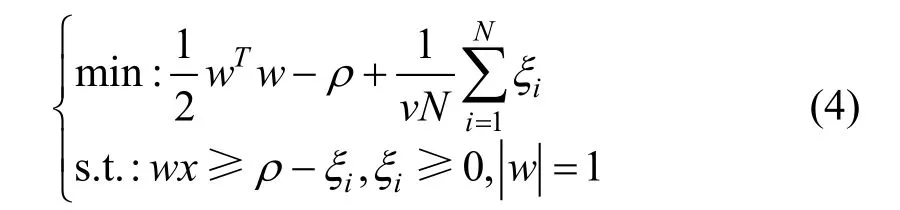
公式中的v是异常点比例的上界,因此可以通过设置参数来限制正例数据集中被划分为异常点的样本数量,从而模型划分的正例子集样本量较少导致的估计偏差。同时,当设置异常点比例上界较大时,此时的超球体半径较小,模型划分为正例的样本可以作为可信赖的正例样本。
在正例标签频率的估计上,估计值可以通过切比雪夫不等式给出。通过切比雪夫不等式,正例子集S中标签样本的数量LS满足公式(5)。
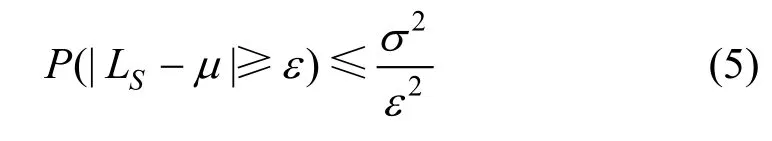
其中LS服从二项分布,且随机变量LS的期望为E(L) = cNS,方差为 D (L ) = c ( 1 - c )NS,NS为正例子集S的样本总数。代入公式(5)得到:
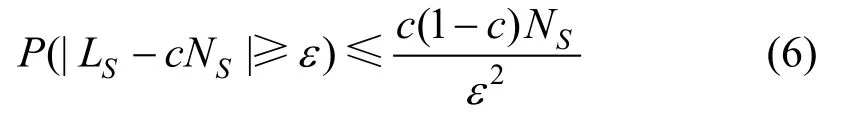
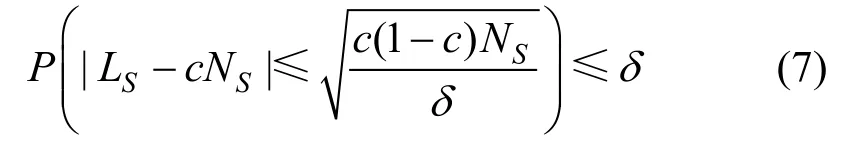
通过公式(7),可以以概率δ对正例标签频率c的上界和下界进行约束,如公式(8)所示。

在TIcE算法中,由于发现可信赖正例子集的算法是决策树,随着决策树划分的进行,叶子节点的数量减少,会存在一些叶子节点脱离真实样本混合比例,故在算法中选择类先验概率估计的下界进行约束。然而,通过OCSVM算法划分可信赖的正例子集,可以对正例子集样本数进行约束,因此可以取区间中点作为对正例标签频率c的估计值,进而可以计算出类先验概率,称该类先验概率估计算法为OCSVM-cE。
OCSVM 相较于 TIcE算法,首先将寻找正例子集的算法由决策树转换成OCSVM,这样做一方面可以通过 OCSVM 模型的参数对可信赖正例子集的样本数进行限制,避免由于可信赖正例子集样本过少导致的估计偏差,另一方面在训练模型所使用的数据上进行了优化,TIcE在构建决策树时需要同时使用正例数据集和无标签数据集,这也导致在通过TIcE算法估计类先验概率时,需要根据不同的无标签数据集重复构建决策树,在实际应用中开销较大。然而OCSVM-cE算法在构建模型时仅需要正例数据集,训练的模型可以在不同的无标签数据集中使用,因此在训练好模型之后,OCSVM-cE算法的时间复杂度降至O(n)。
算法2.OCSVM-cE算法
输入: 正例标签数据集 P,无标签数据集 U,OCSVM的误差上界δ
输出: 类先验概率π
1: Load dataset P and U;
2: NP= l en(P),NU= l en(U);
3: Data normalization;
4: Set upper bound on the fraction of training errors as δ,train an OCSVM model;
5: Merge P and U as A,predict A through OCSVM model;
6: Count the number of samples identified as positive examples in P and U as nPand nU;
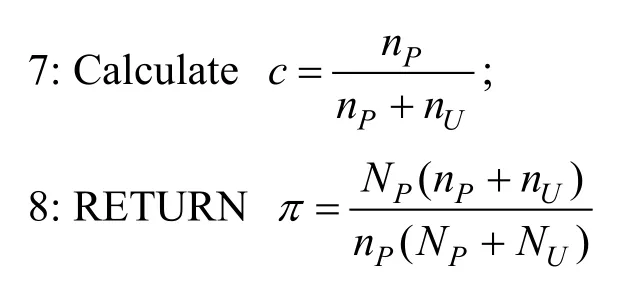
通过算法 2可以在对待检测的工控数据进行分析,估计其类先验概率,为PU学习提供重要的先验知识,同时避免了采集工业控制系统入侵检测数据,极大的减少了人工成本。
3.3 基于神经网络的PU学习
在工业控制系统中,入侵具有较高的隐蔽性且更新较快,从“Stuxnet”到“Duqu”,再到“Flame”火焰病毒,传统的基于分类的入侵检测技术难以应对其更新,而将入侵检测作为异常检测处理,虽然无法识别入侵的种类,但是可以在面对未知入侵时也具有示警的能力。本文采用PU学习方法进行入侵检测,将正常流量作为标签数据,与待检测的数据同时参与模型的训练,同异常检测算法一样,PU学习方法具有检测未知攻击的能力,同时其被证明了训练的模型具有接近二分类模型的准确率。
3.3.1 数据不平衡下的PU学习
PU学习中将无标签数据集视为带有噪声标签样本的反例数据集,进而通过类先验概率估计二分类损失。二分类损失的期望计算如公式(9)所示:
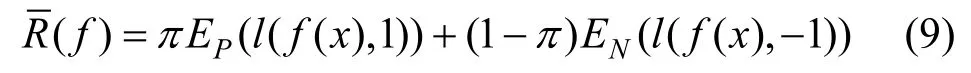
然而在PU学习中,没有带标签的反例样本,因此无法直接计算反例样本的损失,nnPU中提出通过无标签数据集去估计反例样本损失,这也是nnPU的核心思想。无标签数据集混合了正例和反例样本,将其视为含有错误标签样本的反例数据集,那么其损失的期望可以表述如下:
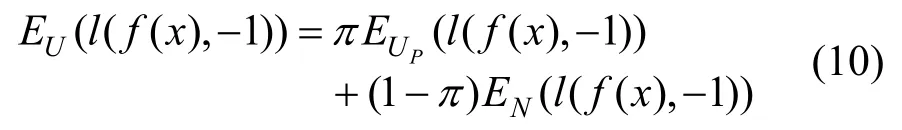
其中π为无标签数据集中的类先验概率,l为损失函数,UP为无标签数据集中的正例样本集合。在公式(10)中,EU(l(f(x),-1 ))可以直接计算,EN(l(f(x),- 1 ))是待估计的反例样本损失,因而问题转换成计算出 EUP(l(f(x),-1 ))。
在TS场景下正例标签数据集和无标签数据集均通过随机采样获得,故正例标签数据集损失的期望和无标签数据集中正例样本损失的期望近似,有:
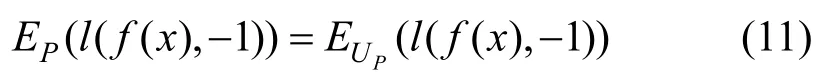
联立公式(10)和公式(11)可以得到估计二分类误差的方法,如公式(12)所示。
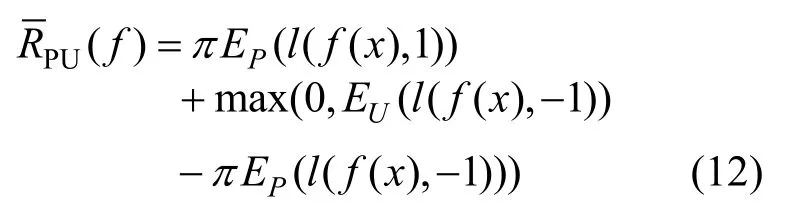
公式被称为Non-negative risk estimator[40],其中,max(0,EU(l(f(x) ,- 1 )) -πEP(l(f(x),- 1 )))是估计的反例样本损失,EP(l(f(x) ,1))是正例样本损失的期望。
在进行入侵检测时,将正常流量作为正例样本,这样在待检测的无标签数据集中正例样本的比例通常远大于反例,存在数据不平衡问题。
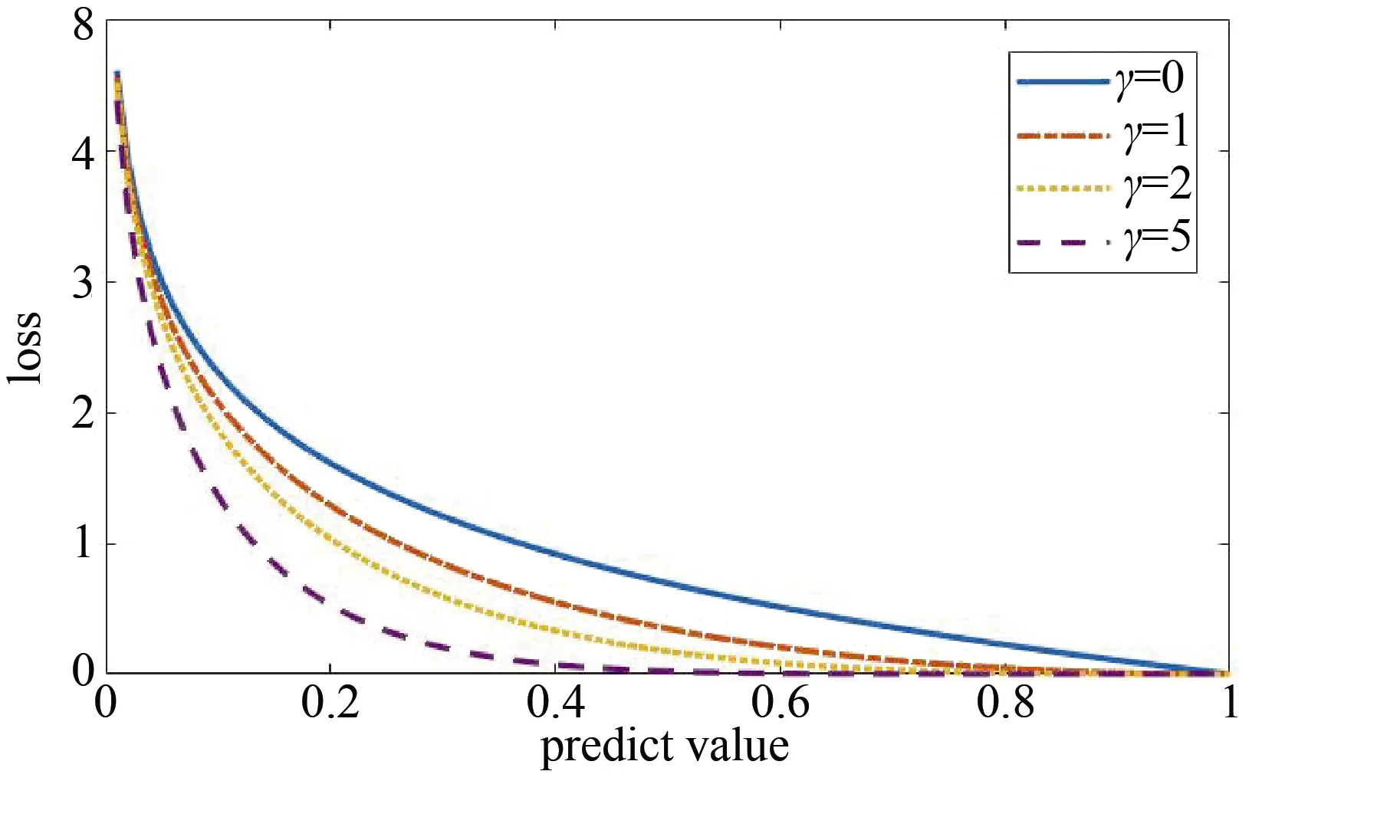
图4 y=1时focal loss函数图像Figure 4 Image of focal loss function when y=1
为了应对由于类先验概率较小导致的数据不平衡问题,PU学习的损失函数设定为focal loss,如图2所示,focal loss可以写成:

在模型的训练过程中,正例样本识别错误时会被作为难分样本,此时(f(xi) )γ和(1 -f(xi) )γ存在数十倍甚至数百倍的差距,可以增大难分样本的权重,提升nnPU在数据不平衡下的分类性能。修正之后的Non-negative risk estimator 如公式(14)所示。

PU 学习的算法伪代码如算法3所示。
算法3.PU学习算法
输入: 正例标签数据集P,无标签数据集U,epochs,学习率γ,batch_size
输出: 无标签数据集中样本的预测值
1: Load datasetPandU,Data preprocessing and data normalization;
2: define a neural network;
3: Weight initialization;
4: FORk=1 TOepochs,DO
5: Forward propagation;
6: Calculate risk estimatorR(fl);
8: IF Satisfied early stopping conditions THEN
9: Break;
10: END IF;
11: END FOR
12: PredictUthrough the trained model;
13: RETURN the labels ofU
通过以上分析可知,PU学习相较于二分类模型,在误差计算上进行调整,通过risk estimator估计二分类误差,以估计的二分类的误差进行反向传播,调整神经网络模型的参数。
3.3.2 神经网络设置
使用机器学习方法进行工业控制系统入侵检测的过程中,需要关注工业控制系统对模型的实时性要求,要求模型对输入的数据可以快速做出判定,因此在使用的神经网络结构需要尽可能简化,一方面简化的模型可以减少检测的响应时间,提高模型的实时性; 另一方面可以降低对计算资源的需求,更加符合工业控制系统的应用场景。
PU 学习是一种依托于神经网络的学习算法,在仅有一类标签数据的场景下,通过估计分类误差来训练神经网络模型。神经网络结构的不同,同样也会对模型性能产生影响,在本节中我们探讨两种不同网络结构的PU学习模型。
第一种是全连接的神经网络DNN。DNN是具有多个隐藏层的神经网络,理论上DNN可以拟合任意函数,文献[42]中探讨了不同隐藏层数量的 DNN在入侵检测中的分类性能,且其结果显示在进行二分类时,含3个隐藏层的DNN模型就可以拥有比较高的分类性能,并且随着层数的增加,分类性能没有明显提升。因此本文中选用含3个隐藏层DNN模型,三个隐藏的节点数分别为256、64、16。模型的网络结构设置如表3所示。
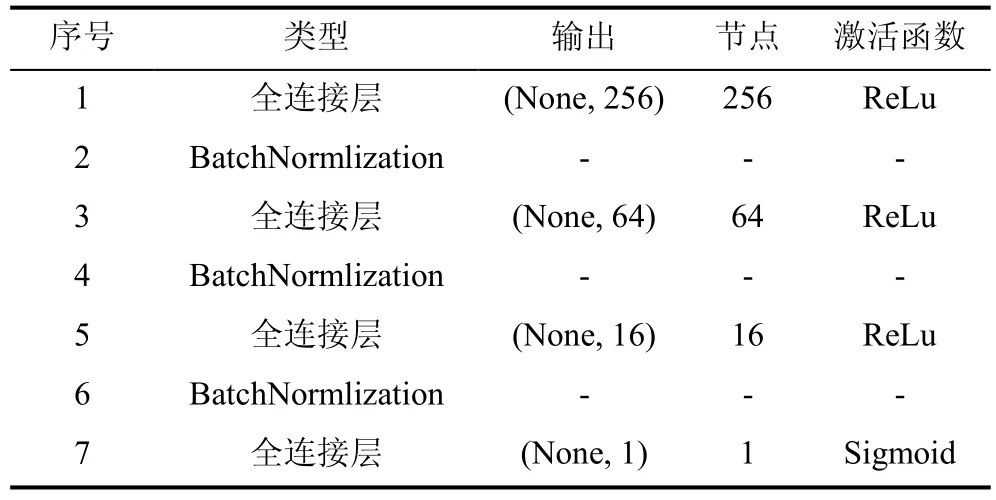
表3 DNN网络设置Table 3 Configuration of DNN model
PU学习通过 DNN完成一个二分类任务,将所有待检测的样本划分为正常流量和入侵流量,DNN的输出通过Sigmoid函数映射到[0,1]区间内,以完成二分类任务。
DNN中在两个全连接层之间进行批量标准化(Batch Normalization,BN),即将每个隐层神经元的输出进行标准化,使得非线性变换函数的输入值落入对输入比较敏感的区域。使用BN可以加速神经网络的收敛,此外BN允许模型使用更高的学习率,并降低模型对于网络参数初始化的要求,其还可以充当调节器,在某些情况下可以消除对Dropout的需求[42]。
DNN中的激活函数选用的是ReLu函数,(1)可以加速网络训练。相比于sigmoid、tanh,其求导更加迅速。(2)防止梯度消失。当数值过大或者过小,sigmoid,tanh的导数接近于0,ReLu为非饱和激活函数不存在这种现象。(3)使网格具有稀疏性。
权重更新算法选用Adam算法,Adam是一种自适应学习率的优化算法,具有收敛快,内存占用少的优点。
第二种是卷积神经网络 CNN。在本文中,采用了一种简单的CNN网络结构Lenet-5结构。考虑到Lenet-5是处理二维图像的网络,要求输入为32×32,而工业控制系统的数据通常为一维向量,因此对网络结构进行调整,替换Lenet-5中的二维卷积为一维卷积,此时输入大小为32×1。因而在进行训练模型前需要进行特征选择,降维到32维。网络中第一层使用5×1的卷积,通过第一层后得到6个大小为28×1的特征图,然后通过大小为2的最大池化采样,变化成14×1大小,第二个卷积层使用5×1的卷积,输出16个大小为10×1的特征图,再通过大小为2的最大池化采样,变化成5×1,最后将所有图像铺平输入到一个全连接层中,全连接层有两层,第一层神经元数量为120,第二层神经元数量为 84,最后按照分类的类别,通过softmax函数进行输出。基于Lenet-5的工业控制系统模型结构如图5所示。其中输入(?,32,1)中的?代表batch_size,激活函数采用Relu函数。
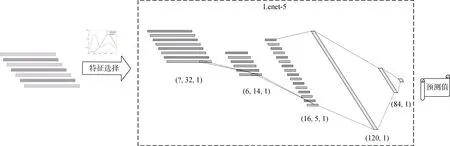
图5 基于CNN的PU学习入侵检测模型结构Figure 5 PU learning for intrusion detection architecture based on CNN
至此,可以得到基于PU学习的模型结构。基于PU学习的入侵检测的模型离线训练步骤如下:
Step 1.读取数据,包括正例标签数据和待检测的无标签数据,进行数据预处理;
Step 2.通过OCSVM-cE算法估计无标签数据集的类先验概率,保存OCSVM模型;
Step 3.通过 KL散度计算特征重要度,设定阈值th或选用的特征数K,按照特征重要度进行特征选择,得到新的训练数据集;
Step 4.初始化一个深度神经网络,使用特征选择后的新训练数据集训练 PU学习模型,训练的过程如算法3所示;
Step 5.导出训练好的神经网络,返回无标签数据集的预测值。
4 实验结果与分析
4.1 数据介绍与分析
实验中使用了三个入侵检测公开数据集:NSL-KDD①下载地址: https://www.unb.ca/cic/datasets/nsl.html.[43],UNSW-NB15②下载地址: https://www.unsw.adfa.edu.au/unsw-canberra-cyber/cybersecurity/ADFA-NB15-Datasets/.[44]和 WADI③下载地址: https://itrust.sutd.edu.sg/itrust-labs_datasets/[45]。其中NSL-KDD和UNSW-NB15数据集中的数据是基于互联网流量提取的特征,包含流的基本特征(如传输层协议类型、端口等)、流的时间信息、连接内容特征等,这些特征也可以作为工业控制系统流量进行提取。同时,为了进一步验证模型在工控场景下的有效性,引入了WADI数据集,一方面在数据上应用工控试验台提供的工控数据; 另一方面,仿真工控数据不平衡特点。
在攻击类型上,NSL-KDD数据集是在KDDCUP 99数据集上进行了改进,去除了一些冗余数据,数据集中包含了正常流量和22类攻击流量,攻击流量主要有: 拒绝服务攻击 DOS,监视和探测(Probing),远程机器非法访问(R2L)和普通用户的越权访问(U2R)四大类。UNSW_NB15数据集是由澳大利亚网络安全中心生成的入侵检测数据集,包括 DOS、Backdoors等在内的9种攻击的样本。WADI数据集是在配属试验台上收集的,实验台由许多向用户水箱供水的大型水箱组成,WADI数据集种包含16种攻击,其攻击目标是停止向用户水箱供水。
在实验中,UNSW-NB15数据集,采用的官网提供的训练和测试数据集,合共257673个样本。WADI数据集采用的是2019年10月的带标签的数据。各数据集的样本量如表4所示。
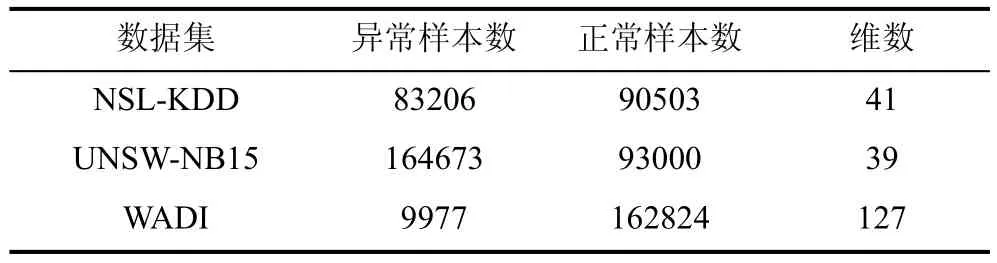
表4 实验数据集信息Table 4 Information of experiment data set
4.2 数据预处理
训练和测试数据集划分上,基于样本的真实标签,在正例数据中随机抽取指定数量的正例样本作为训练集,剩下的数据作为测试集。数据处理上,针对NSL-KDD存在的字符串数据,如协议类型和服务,需要进行独热编码将字符串转换成一个向量,编码之后的NSL-KDD数据集维数从41维提升到122维。UNSW-NB15和 WADI数据集中的数据不存在空值和字符串,因此可以直接使用。
本实验中采用的设备: 处理器为 Intel core i7 8750H,操作系统为64位Windows 10家庭中文版,硬盘为西数SN720,内存16 G。
4.3 评价指标
训练好模型之后,通过模型对待预测的数据集进行分类,基于模型的判定结果,可以建立如表5的混淆矩阵:

表5 混淆矩阵Table 5 Confusion matrix
如表2~5所示,行表示是数据的真实类别,列表示模型的预测类别。在入侵检测中关注的是模型对于入侵样本的识别能力,因此使用入侵样本的查准率和召回率作为评价指标,查准率如公式所示,查准率描述的是模型预测为正例的样本中,真实标签为正例的比例,如公式(15)所示。

表2 二分类的特征重要度计算方法Table 2 Method for calculating feature importance of binary classification
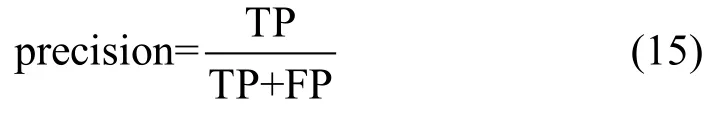
召回率如公式(16)所示,召回率描述的是模型将所有真实类别为正例的样本识别为正例的比例。
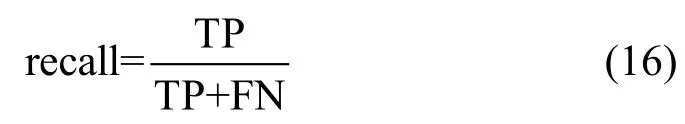
F1-score也常被用于作为评价指标,F1-score是查准率和召回率的调和平均值,如公式(17)所示。
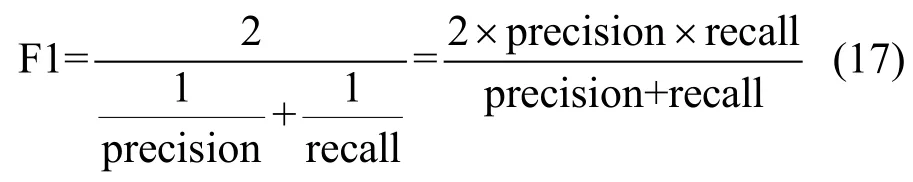
除了以上指标,在入侵检测场景中,由于面对的数据量较大,因此,模型训练和预测所用的时间也是衡量模型性能的一个重要指标。
4.4 实验结果分析
(1) 特征重要度的有效性分析和时间效率
本实验中,首先在二分类场景下通过随机森林计算各个特征的重要度,并将其与基于KL散度计算的特征重要度进行对比,验证使用KL散度计算的特征权重的有效性。
实验中,在所有样本中随机抽取2000个正例样本作为正例标签数据集,再抽取2000个正例样本和4000个反例样本混合作为无标签数据集,余下的所有样本作为测试集。图6和图7分别展示了 KLOCSVM和KDE-OCSVM算法在NSL-KDD数据集和UNSW-NB15数据集中的实验结果。
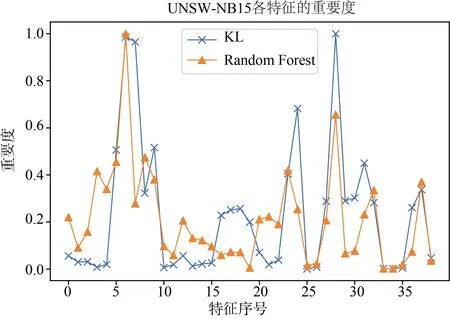
图6 UNSW-NB15特征重要度Figure 6 Feature importance on UNSW-NB15
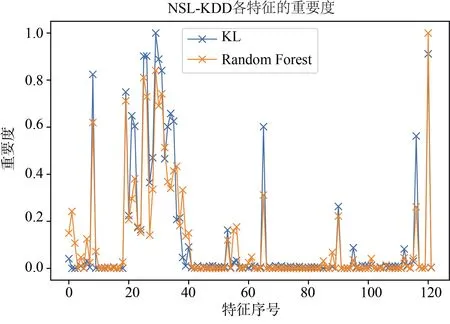
图7 NSL-KDD特征重要度Figure 7 Feature importance on NSL-KDD
进一步地,计算两种算法所得特征重要度的相关性并进行相关性检验。通过计算,在UNSW-NB15数据集下,两种算法的特征重要度在归一化之后的相关系数均值为 0.72,检验的P值为 4.29× 1 0-7,NSL-KDD数据集上的相关系数为0.9364,检验的P值为 1.15× 1 0-56。以显著性水平为0.05,可以认定通过 KL散度计算出的特征重要性和在二分类情况下的特征重要性存在显著的相关关系,即通过KL散度计算的特征重要度是有效的。
(2) 类先验概率估计
为了验证本文提出的OCSVM-cE算法的有效性,将其与以下类先验概率算法进行比较:
· KM1/KM2算法。该算法由Ramaswamy等人[31]在2016年提出,该算法通过计算正例和反例数据集的分布嵌入到核空间中,通过求解一个二次规划问题即可解得类先验概率,该算法是目前估计准确率较高的算法。
· TIcE算法。该算法由Jessa Bekker[36]在2019年提出,该算法基于决策树对所有样本进行划分,通过子集提升正例样本标签频率下界,得到正例样本标签频率的估计值,进而计算出类先验概率,该算法是目前类先验概率估计时间复杂度最低的算法。
· OCSVM-cE算法。本文中提出的算法,训练OCSVM 模型寻找无标签数据集的可信赖正例子集,通过可信赖正例子集估计正例样本标签频率,进而计算出类先验概率。
类先验概率估计问题中,核心的评价指标是估计的准确率,即估计值和真实值的误差。此外,算法的时间复杂度也是一项重要的评价指标。
基于以上评价指标设计如下两个实验进行验证:1) 验证类先验概率估计的准确度,在实验中以不同的类先验概率构造无标签数据集,并通过四种不同的基线算法估计构造的无标签数据集的类先验概率,分析不同算法估计值与真实值的误差; 2) 验证算法的时间复杂度。在该实验中首先比较同样本量下各算法进行类先验概率估计所需的时间,然后在不同样本量下估计类先验概率时间变化趋势。
首先是类先验概率估计的准确率。实验中,设置正例标签数据集样本量为 1000,无标签数据集中反例样本为2000,分别构造类先验概率为: 0.1,0.2,0.3,0.4,0.5的无标签数据集。分别使用基线算法对构造的数据集进行类先验概率估计。
实验结果如图8和图9所示。图中横坐标为真实类先验概率,纵坐标为估计值和预测值误差的绝对值。实验结果显示,OCSVM-cE算法在两个数据集上都能保持较高的预测准确度,误差和KM2算法接近且维持在0.05以下,算法估计的稳定性较好。
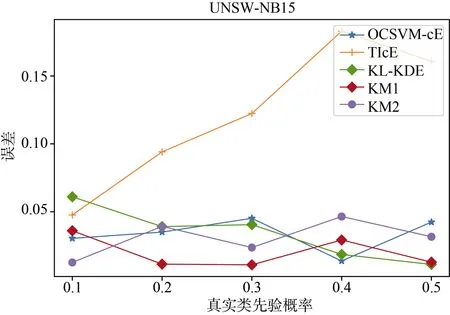
图8 UNSW-NB15类先验概率误差Figure 8 Class prior estimation error of UNSW-NB15
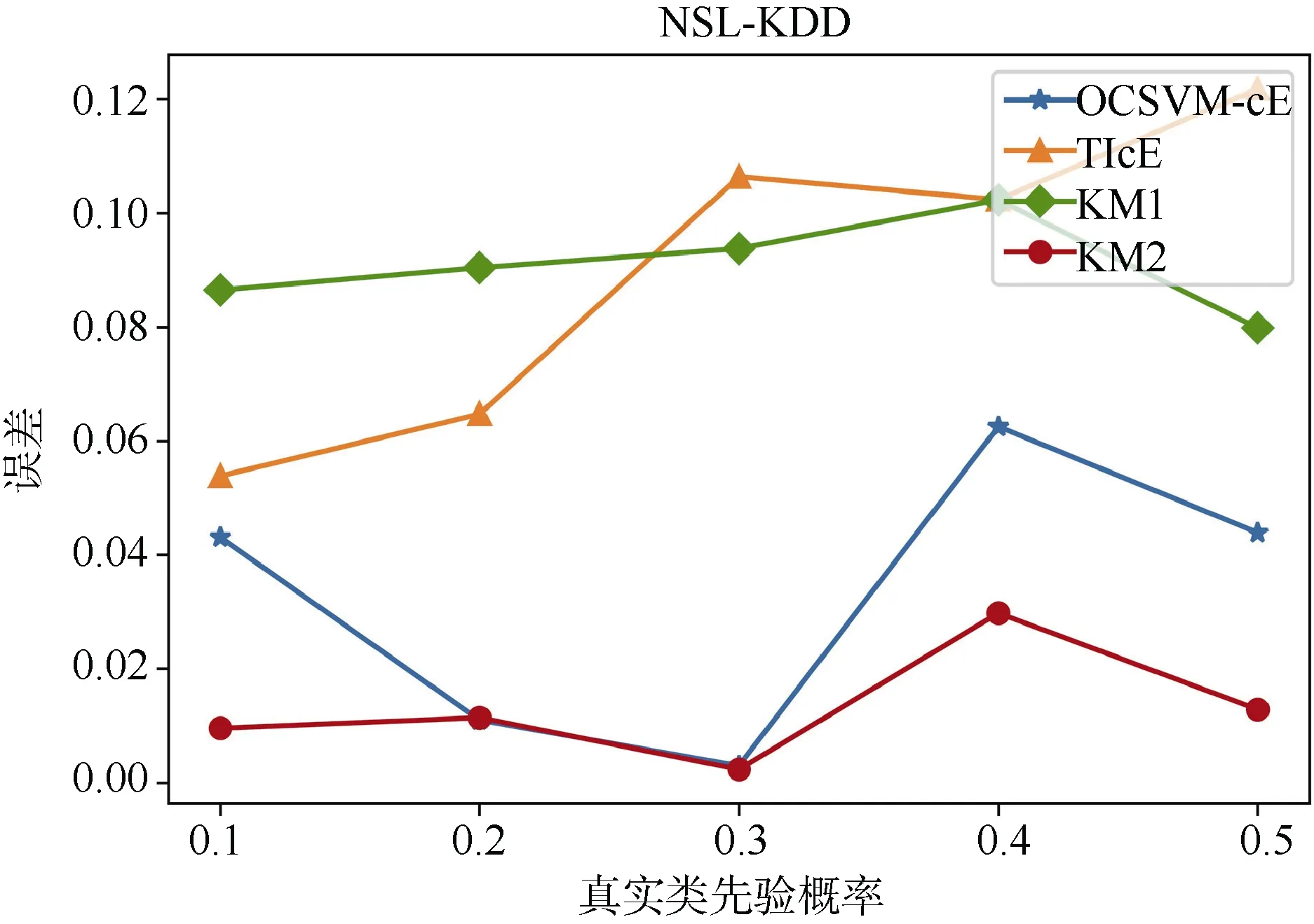
图9 NSL-KDD类先验概率误差Figure 9 Class prior estimation error of NSL-KDD
在实验过程中,TIcE算法存在较大的正误差,这是由于TIcE算法通过求标签频率的下界去估计真实标签频率,这将导致估计的标签频率比真实值低,因此估计的类先验概率比真实值大,在 OCSVM-cE算法中,通过 OCSVM 算法寻找可信赖的正例子集,避免使用下界,提升了估计的准确率。
为了进一步检验OCSVM-cE算法估计的稳定性,设置正例标签数据集样本数为2000,在[0.1,0.9]区间内随机取值作为类先验概率构造无标签数据集,重复进行 100次实验,计算类先验概率估计值和真实值的误差。
图10中展示了100次重复实验的箱线图,可以发现OCSVM-cE算法在KDD和UNSW-NB15数据集上的预计效果比 WADI数据集上更好,估计的误差上四分数小于 0.05,而 WADI数据集上估计的误差的下四分位数为0.0407,中位数为0.0672,上四分位数为0.0884,仅存在两个异常点,因此WADI的估计值比较稳定,且误差集中在[0.05,01]区间内,综合三个数据集的估计结果,OCSVM-cE是一种稳定的类先验概率估计算法。
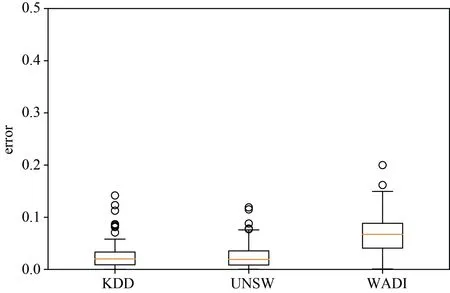
图10 类先验概率误差箱线图Figure 10 Boxplot of class prior estimation error
在 PU学习中,类先验概率是重要的先验知识,其估计的误差将直接影响训练的模型的性能,通过实验进一步探讨类先验概率估计误差对模型性能的影响。实验中设置无标签数据集真实类先验概率为0.4,在[0,1]区间中以0.05为间距取不同的值作为类先验概率的估计值进行实验,结果如图11所示。图11是在 UNSW-NB15数据集下,设置正例标签样本数为10000,无标签数据集中的反例样本数为20000的实验结果。其中横坐标为估计的类先验概率,纵坐标为F1-score。可以看到,当估计的类先验概率为0.4时,F1-score达到最大值,此时模型的性能是最好的,并且随着估计的类先验概率和真实类先验概率误差的增大,F1-score开始下降,当估计值为0时所有无标签样本被划分为反例,当估计值为1时,所有无标签样本被划分为正例。从F1-score分析,估计的类先验概率误差应当小于0.05可以保证模型具有较好的分类性能。
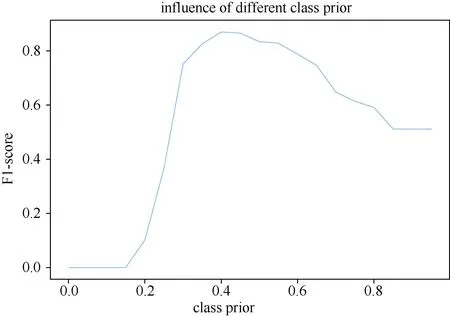
图11 不同类先验概率估计值对F1-score的影响Figure 11 Influence of different estimated class prior to F1-score
图12显示,在固定正例样本数为 1000时,OCSVM-cE算法和 TIcE算法所需的时间与无标签样本数成正相关。考虑到 OCSVM-cE中,训练OCSVM模型仅需要使用到正例样本,因此可以认为OCSVM-cE算法更加贴合入侵检测应用场景,其过程中训练的 OCSVM 模型是可以复用的,在对新无标签数据集进行类先验概率估计时,可以直接加载模型,来划分可信赖的正例子集。
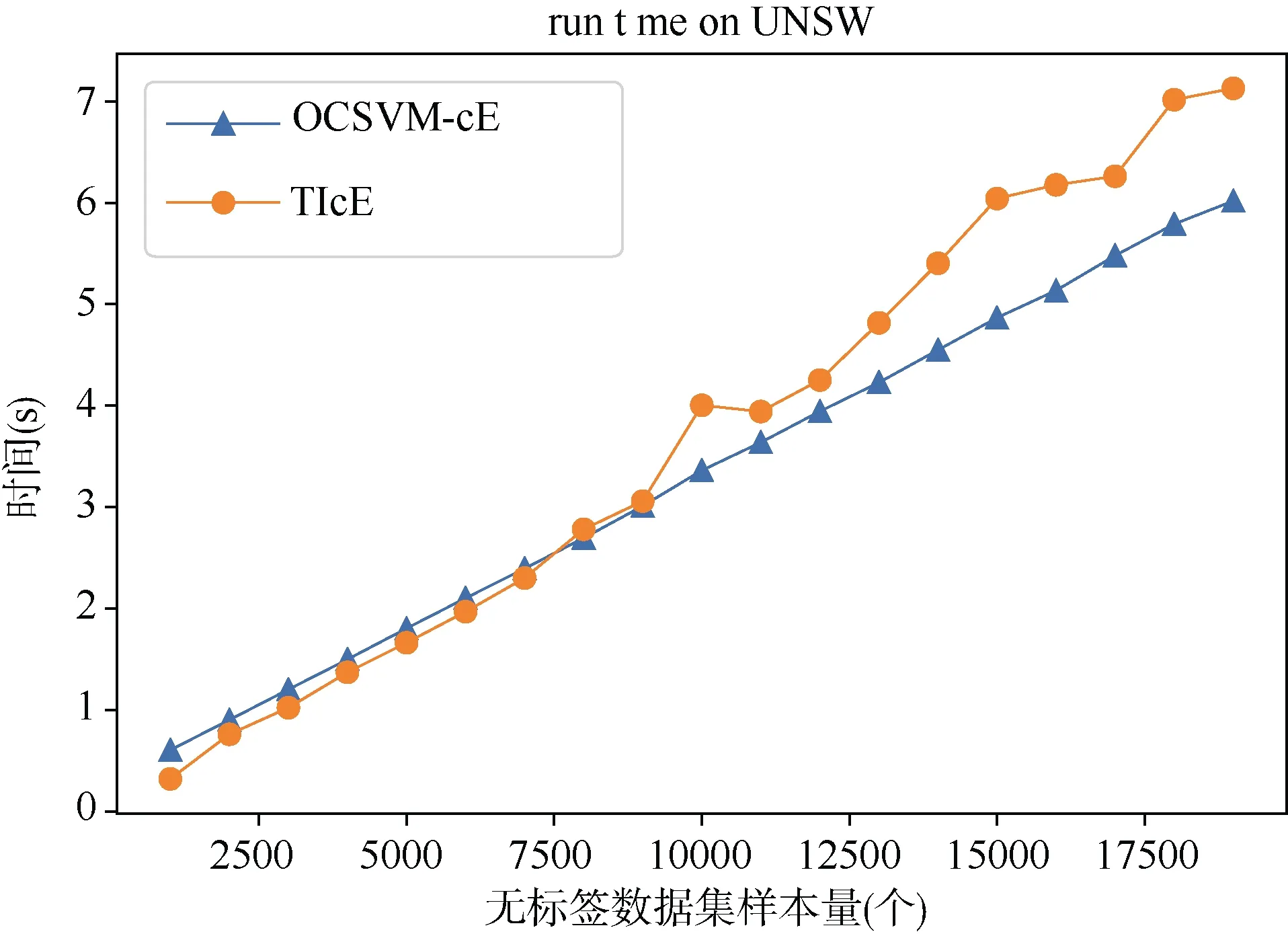
图12 UNSW-NB15数据集不同样本量估计时间Figure 12 Estimation time of UNSW_NB15 with different sample size
(3) PU学习性能分析
对比的二分类模型的神经网络设置: DNN的设置与PU学习所用的DNN网络模型一样,模型中包含三个隐含层,第一层的神经元数量为 256,第二层神经元数量为 64,第三层神经元数量为 16,但是在训练的过程中使用具有真实标签的正例和反例样本进行训练; CNN的网络结构使用和文献[46]相同的LeNet-5结构,输入为32×32的图像,第一层使用5×5的卷积,通过第一层后得到 6个大小为28×28的特征图,并通过2×2的最大池化采样,变化成14×14大小,第二个卷积层使用5×5的卷积,输出16个大小为10×10的特征图,然后通过2×2的最大池化采样,变化成5×5,最后将所有图像铺平输入到一个全连接层中,第一层神经元数量为 120,第二层神经元数量为 84,最后按照分类的类别,通过softmax函数进行输出; RNN[47]中设置隐藏层节点数为80。
实验中设置正例标签样本数为10000,无标签数据集中的反例样本数为2000,类先验概率为0.9,学习率为0.01,迭代次数为50。
表6为PU学习与二分类模型对比结果,表中的对比实验可以分为两类: 同网络结构(DNN/CNN)下PU学习和二分类性能对比,PU学习和目前性能较好的二分类模型的对比。从实验结果来看,同网络结构下PU学习的性能与二分类模型在查准率上近似,但是召回率存在一定的差距,根据前文的分析,工控入侵检测对于模型的查准率要求更高,期望做到“宁可漏报也不误报”,因此 PU 学习是适用于工控入侵检测的,同时相较于目前先进的CNN-BiLSTM等模型,在查准率上依旧可以维持较小的差距。同时 PU学习对比二分类模型,降低了训练数据的要求,只需要一类标签数据,这可以有效的减少数据采集工作,同时仅通过正例数据和无标签数据进行训练,使得模型可以挖掘出未知类型的入侵。
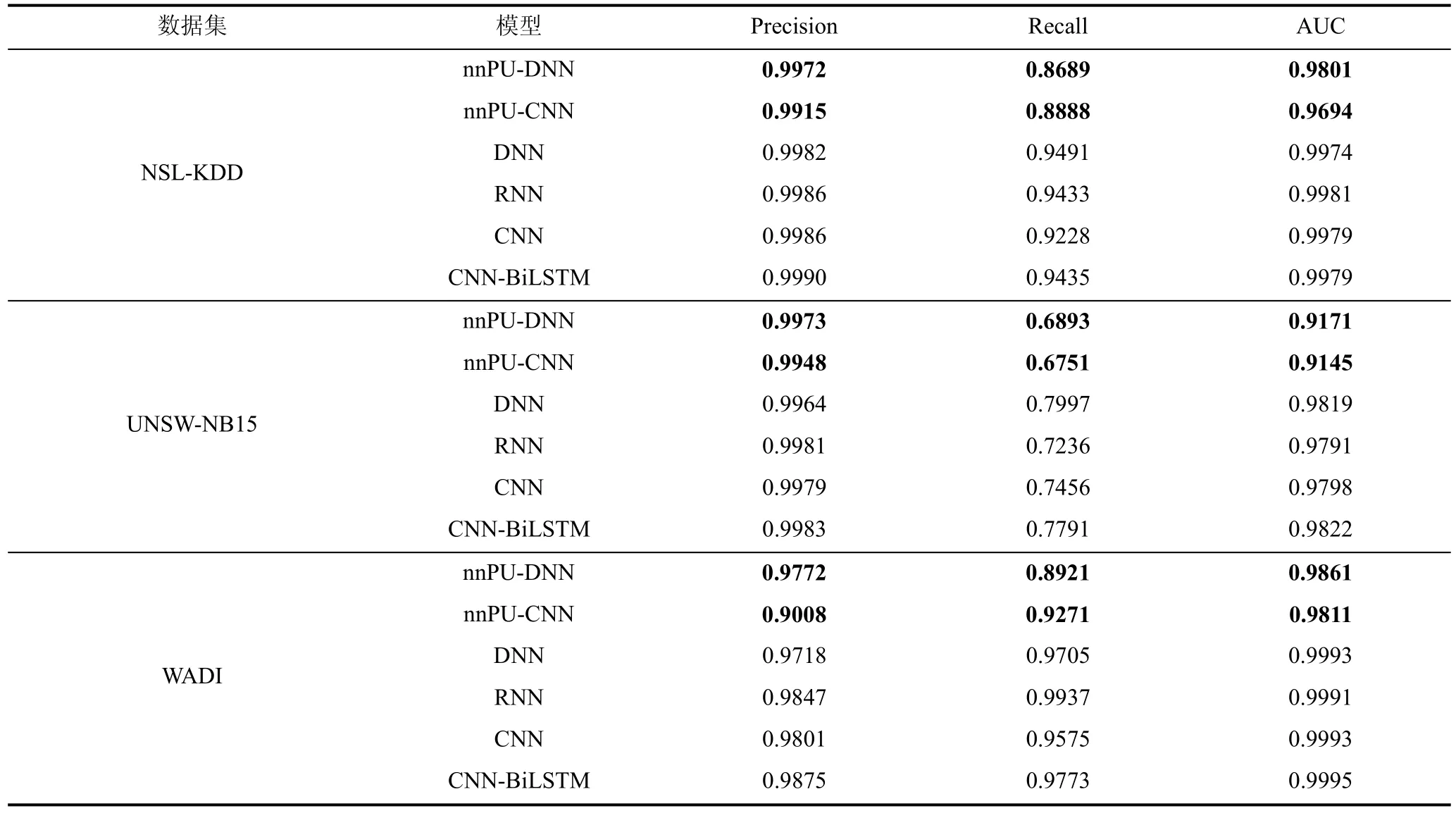
表6 PU学习与二分类模型对比结果Table 6 Comparison result of PU learning with binary classification
表6中实验对比了PU学习和二分类模型的性能,接下来将对比PU学习和异常检测模型,分析同样在仅有一类标签数据的条件下,二者性能差异。从表1中列举的研究分析,目前用于入侵检测的异常检测模型主要为AE和OCSVM,其中AE是无监督模型,AE包含两个部分: Encoder(编码器)和 Decoder(解码器)。Encoder的作用是用来发现给定数据的压缩表示,Decoder是用来重建原始输入,通过计算重建输入和原始输入的误差进行异常检测,表1中文献[13]、文献[20]和文献[25]在使用 AE模型上大同小异,因此本文选择采用文献[13]提出的模型①源码下载地址: https://github.com/Battlingboy/AE-IDS进行对比实验;同时,纵观OCSVM进行入侵检测的研究,其主要工作集中在特征工程上,本实验中基于PU学习的特征重要度量进行特征选择,结合 OCSVM 进行异常检测。参数设置上,OCSVM设置误差上界为0.1,AE的参数采用源码中的默认设置。
表7为PU学习与异常检测模型的对比结果,表中的指标显示,特别地,可以观察到OCSVM和AE在 WADI数据集上模型的性能较差,造成这种情况是因为测试数据不平衡,测试数据集中正例数据与反例数据的比约为 16︰1,这也说明了 OCSVM 和AE算法在处理不平衡数据时存在不足,而PU学习通过 focal loss提升了模型在不平衡数据下的性能,因此PU学习在查准率和召回率上都有明显提升,在三个数据集上,PU学习在查准率上均表现明显优与AE和OCSVM。
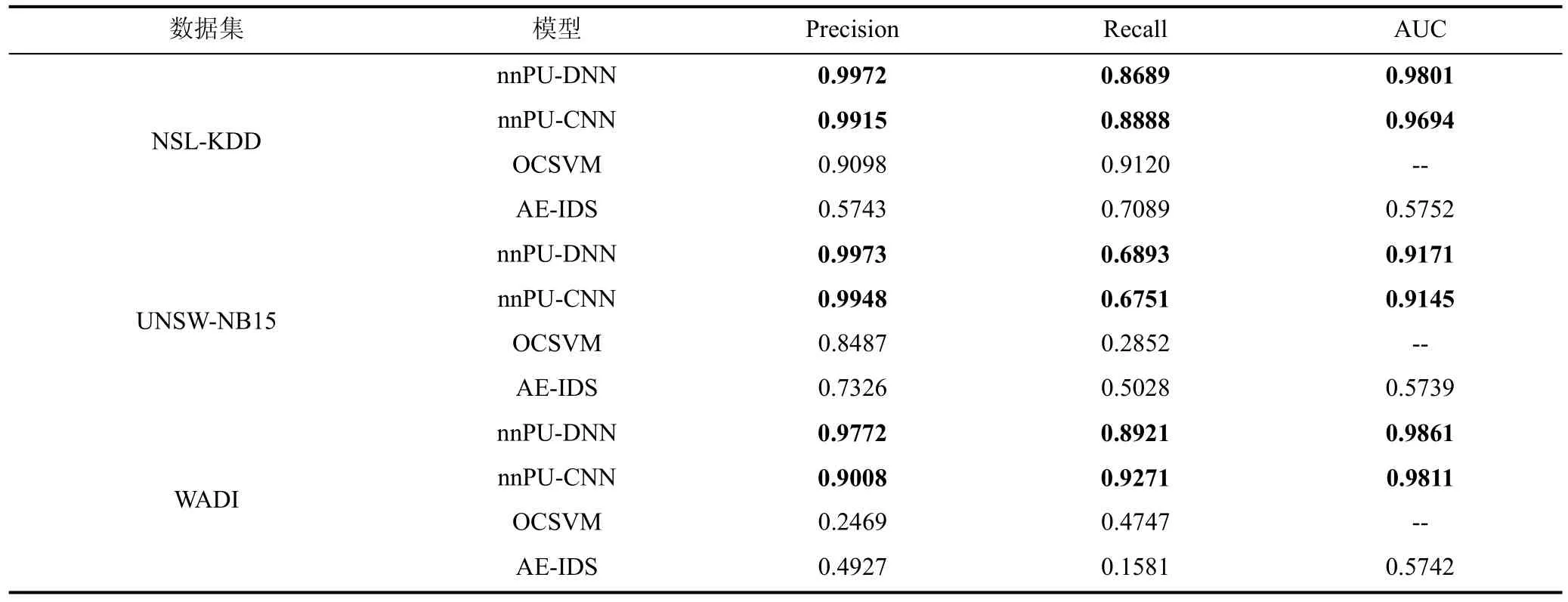
表7 PU学习与异常检测模型对比结果Table 7 Comparison result of PU learning with anomaly detection
结合表6和表7的结果,不难发现,PU学习尽管在训练数据上同异常检测算法类似,仅需要一类标签数据,但是训练的模型的分类性能相较于异常检测算法有较大的提升,特别地在工控场景下以WADI数据集为例,正常数据与异常数据之比高达16︰1,PU学习同样可以维持较高的查准率和查全率,同一些二分类算法相比,在查准率上也仅有细微的差距,结合前文对于工控场景特点,PU学习是适合于工控场景异常检测的。
综上所述,本文提出使用PU学习进行入侵检测,PU学习是一种近似于异常检测的算法,但在训练数据上需要标签正例数据,且正例数据需要满足SCAR条件,在此基础上PU学习可以提供高查准率高召回率的入侵检测,其查准率和召回率均较无监督的异常检测模型有明显的提升,特别地,PU学习在查准率上接近二分类模型。
5 结论
工业控制系统被广泛应用到核电、水利等国家重要基础设施中,保障工业控制系统安全是十分重要的,入侵检测系统是作为保障网络安全的重要手段,也是工业控制系统安全防护的重要组成部分。本文中,针对工业控制系统入侵检测,提出使用PU学习进行入侵检测,以正常流量作为标签数据探测待检测数据中的异常样本; 针对工业控制系统数据维度高、关联性强的特点,提出一种特征重要度计算方法用于特征选择; 同时改进类先验概率估计算法,提出 OCSVM-cE算法用于类先验概率估计,提高了估计的稳定性和准确率。最后通过实验验证PU学习的有效性,同有监督二分类模型相比,PU学习的查准率维持在一个较高的水准,召回率略低; 同异常检测模型对比,PU学习在准确率和召回率上均有提升。PU学习尽管其避免了使用反例数据,但是也对正例数据进行了更严格的限制: 正例样本是完全随机采样的,即正例样本的分布与无标签数据集中正例样本的分布相同。这也是PU学习的不足,未来的工作可以围绕如何在具有选择偏差的数据集下进行PU学习。
致 谢本文研究受国防基础科研计划(No.JCKY 2019608B001)资助。
