汽车起重机主副臂结构的几何非线性分析
2021-08-24秦旺林刘士明孟丽霞
秦旺林, 刘士明, 李 聪, 孟丽霞
(沈阳建筑大学 机械工程学院, 辽宁 沈阳 110168)
0 引言
汽车起重机臂架因高层建筑施工需要而变得高耸,长细比增大, 从而导致臂架变形呈现非线性变化而无法预期。 因此, 对汽车起重机臂架的变形分析显得尤为重要,其非线性变形分析成为研究焦点之一[1-2]。 文献[3]采用挠度放大系数法, 得到了伸缩臂端部在承受复杂载荷情况下的挠度表达式。王鑫[4]对大长度伸缩臂的挠度问题进行研究时, 考虑了轴力二阶效应和铰支梁变形对臂架变形的影响。 文献[5]应用Timoshenko 梁理论,采用位移、转角独立插值的方法,获得了适用于变截面梁、等截面梁以及组合式梁杆结构的切线刚度矩阵。王欣[6]针对承受横向均布载荷的压杆进行了几何非线性分析, 提出了一种新的解决方法。 上述文献在对起重机臂架的挠度分析时,理论研究多集中在单一种类臂架。而对于结构复杂的主副臂结构,其挠度问题虽然有一些学者进行了研究,但多是借助有限元软件进行仿真分析[7-8]。 由伸缩主臂与格构式固定副臂组成的主副臂结构为大长细比结构, 采用线性理论计算主副臂结构的变形会引起较大的误差[9],需进行几何非线性分析。 同时《起重机设计规范》GB/T3811-2008中没有给出主副臂结构几何非线性变形的数据和计算公式[10],研究人员也没有给出相关的理论计算公式。
本文以汽车起重机的伸缩主臂与惯性矩沿截面二次变化的格构式固定副臂组成的主副臂结构为研究对象,基于二阶理论, 采用微分方程法建立主副臂结构的挠曲微分方程,获得其挠度表达式。 利用挠度表达式和有限元软件ANSYS 对主副臂结构进行挠度计算,将公式计算结果和仿真结果进行对比分析, 以验证本文所推导的挠度表达式的正确性。
1 主副臂结构挠度表达式的建立
由于汽车起重机变幅油缸的轴向刚度远远大于伸缩臂的侧向刚度, 变幅油缸与伸缩主臂铰接点以下及起重机工作台形成一个稳定的三角形区域, 在工作中这部分基本不会产生变形。 因此,在图1 所示的主副臂结构中,将主副臂实际结构等效为根部固定的悬臂梁,将伸缩主臂部分等效为多级阶梯柱模型, 变截面格构式固定副臂部分等效为惯性矩沿截面二次变化的变截面实腹式模型[6],则图1 实际主副臂结构等效为图2(a)的主副臂结构计算模型。 图2(b)为主副臂结构在轴向力P、 侧向力Q 以及弯矩M 作用下主副臂结构的变形曲线, 臂端挠度值为δ。

图1 具有主副臂结构的起重机施工现场

图2 主副臂结构几何非线性计算模型
图2(a)中,伸缩主臂总长为l,各臂节到固定端的长度为li(i=1,2,…,n),每节伸缩臂的截面惯性矩为Ii(i=1,2,…,n);固定副臂部分长度为b,大端面截面惯性矩Ig1,小端面截面惯性矩为Ig2,副臂任意截面处截面惯性表示为Ig(x)=Ig2(L-x)2/a2,a 为固定副臂锥度部分长度;主副臂结构总长度L=l+b,其材料的弹性模量为E,L=l+a+b。
基于小变形理论, 由图2 列写出考虑轴力二阶效应的主副臂结构挠曲微分方程:
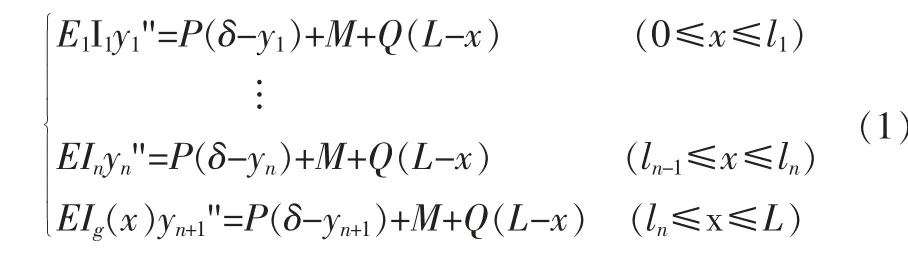
设ki2=P/(EIi)(i=1,2,…,n),则式(1)的通解:
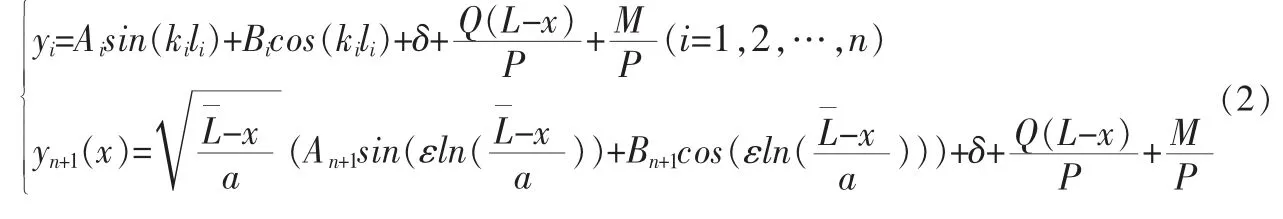

结合式(13)、(14)则式(11)表示为:
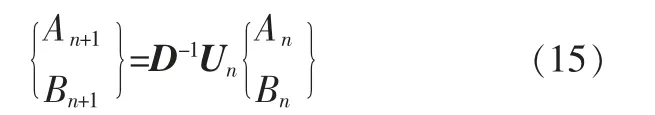
将式(10)代入式(15)中,得到系数An+1、Bn+1的递推表达式:

2 主副臂结构非线性变形的算例分析
以图3 所示6 节伸缩主臂与变截面格构式固定副臂组成的主副臂结构模型为例,在主副臂结构的臂端施加轴向力P、侧向力Q 以及弯矩M,并对其进行非线性变形分析,将有限元软件ANSYS 的仿真分析结果与挠度表达式(20)计算结果进行对比,验证所推挠度表达式的正确性。

图3 6 节伸缩主臂的主副臂结构受力模型
2.1 主副臂结构参数的说明
在图3 中,伸缩主臂总长度l=70m,基本臂截面惯性矩I1=0.04326m4, 各 臂 节 长 度l1=0.2l,l2=0.4l,l3=0.6l,l4=0.8l,l5=0.9l,l6=l, 各臂节截面惯性矩I2=I1/1.3,I3=I2/1.3,I4=I3/1.6,I5=I4/1.6,I6=I5/1.6。 固定副臂部分,锥度系数λ=4,副臂大端面横截面为方形H=0.75m, 主弦杆横截面为方形hx=0.072m,斜腹杆横截面为方形hxf=0.06m,横腹杆横截面为方形hhf=0.06m,斜腹杆与主弦杆的夹角为α,固定副臂单层高0.5m,副臂长度b=0.5n。 主副臂结构总长度L=l+b,弹性模量为E=2.05×1011Pa。 在图4 中给出了工程中常用的4 种四肢变截面格构式结构展开图。
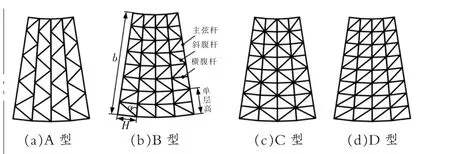
图4 常见变截面构件腹杆布置形式
式(20)计算所用大端面截面惯性矩Ig1=Idx,Idx采用式
(21)计算[11],小端面截面惯性矩Ig2=Ig1/λ2。

式中:Idx—等截面格构式结构等效为实腹式结构的惯性矩;I—肢杆对中性惯性矩之和(I=H2hx2+hx4/3),hx—主弦杆尺寸;η—腹杆影响系数,见表1。
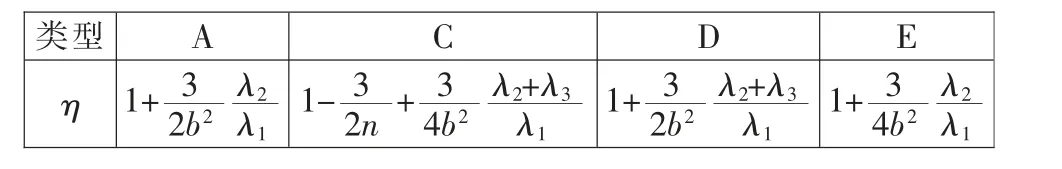
表1 腹杆影响系数
表 中λ1=1/(EAxH2),λ2=1/(EAxfH2cos2αsin2α),λ3=tanα/(EAhf),b—副臂长度,Ax、Axf、Ahf分别为主弦杆截面面积、斜腹杆截面面积、 横腹杆截面面积;H—固定副臂大端面截面尺寸;n—副臂层数。
2.2 算例分析
在ANSYS 中建立6 节伸缩臂与格构式固定副臂的仿真模型见图5, 其伸缩主臂采用Beam44 单元建立,实际的变截面格构式固定副臂采用Beam188 单元建立。

图5 ANSYS 模型
以6 节伸缩主臂和不同固定副臂组成的4 种主副臂结构为例,利用理论公式(20)和有限元软件ANSYS 对由图3 中伸缩主臂与图4 中格构式副臂组成的4 种主副臂结构进行几何非线性分析。表2、表3、表4 和表5 给出给出了A 型、B 型、C 型和D 型4 种主副臂结构在轴向力P=100kN,侧向力Q=30kN 及弯矩M=80kN·m 作用下的挠度值,误差为ANSYS 仿真结果与理论公式式(20)计算结果之间的误差。
由表2、表3、表4 和表5 可知,不同形式的格构式固定副臂组成的4 中主副臂结构, 其理论公式计算结果与ANSYS 仿真分析结果的最大误差分别为0.5%、0.15%、0.86%和0.73%,表2 到表5 理论公式计算结果与仿真分析结果之间误差均小于1%。 算例分析结果表明:本文推导的主副臂结构的非线性变形表达式是正确的, 可以应用于实际主副臂结构的几何非线性变形计算。
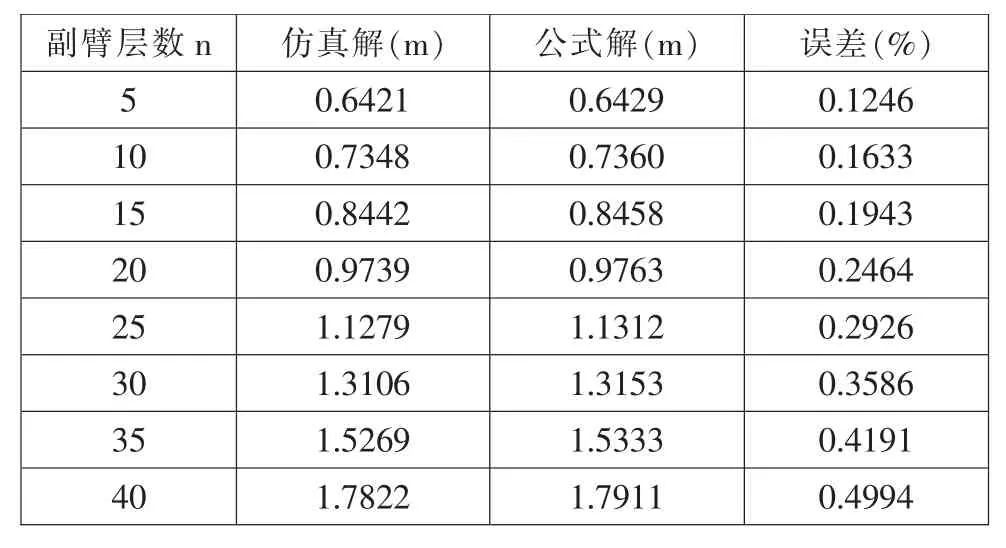
表2 A 型副臂的主副臂结构挠度值
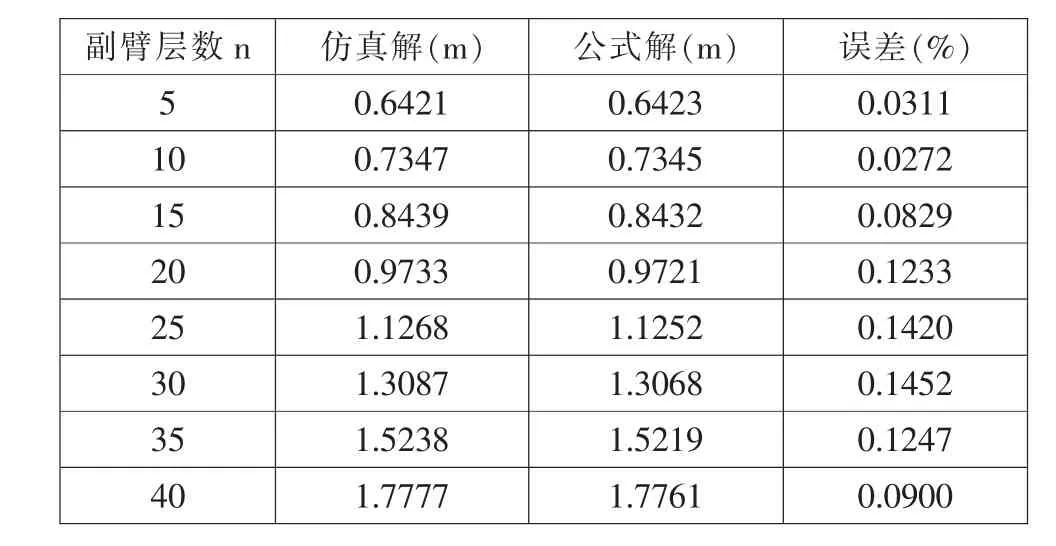
表3 B 型副臂的主副臂结构挠度值
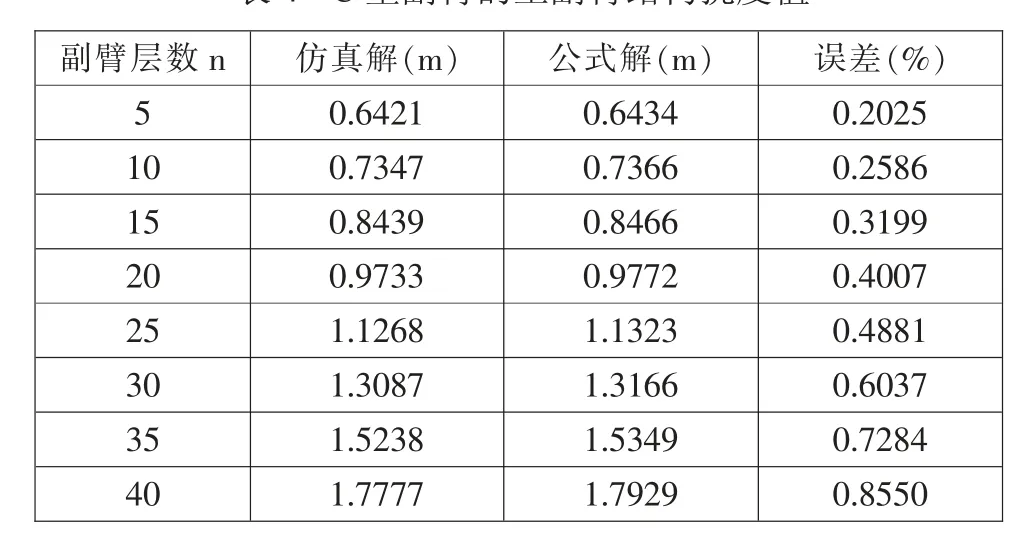
表4 C 型副臂的主副臂结构挠度值
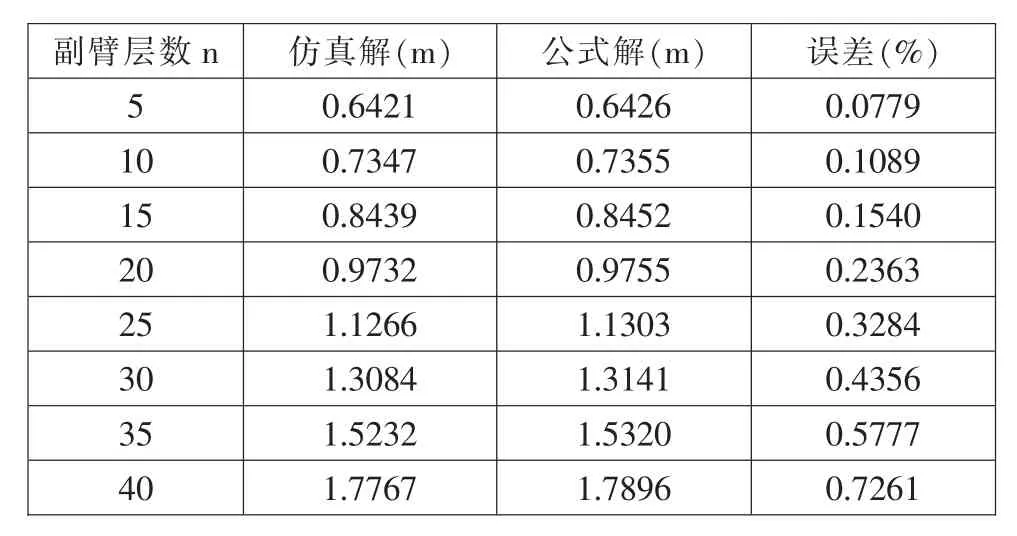
表5 D 型副臂的主副臂结构挠度值
3 结论
本文对伸缩主臂与变截面格构式固定副臂组成的主副结构进行了几何非线性分析,其研究结论如下:
(1)基于纵横弯曲理论,建立了主副臂结构的挠曲微分方程,结合各臂节间的边界条件,推导了以递推形式表示的主副臂结构非线性变形表达式。
(2)利用所推导的非线性变形表达式和ANSYS 仿真,计算了6 节伸缩主臂和不同形式的固定副臂组成的4 种主副臂结构的几何非线性变形, 并将理论公式的计算结果和ANSYS 仿真结果进行对比分析, 其最大误差均在1%以内。
(3)分析结果表明:推导的理论计算公式在对多种副臂形式的主副臂结构进行几何非线性变形计算时, 表现出较高的计算精度, 证明本文推导的主副臂结构非线性变形表达式是正确的,可以满足工程实际应用。
