一类分布最优问题的指数时间收敛算法

刘书新，韩佳敏，杜海霞，曹若薇

（新疆农业大学数理学院，新疆乌鲁木齐，830052）

多智能体系统[1]作为分布式人工智能的一个重要分支，主要研究多个智能体在复杂环境下如何处理协同合作等问题。多智能体系统的一致性问题主要是基于多智能体系统中的智能体相互之间的信息交换，通过设计一致性协议[2]使得智能体的状态趋于一致。近年来，多智能体系统的一致性问题得到了广泛的应用，例如分布式传感器网络、机器人系统的协作等[3]。另一方面,随着人工智能和大数据等新兴领域的发展，基于多智能体一致性的分布式优化理论[4]得到了越来越多的关注，并逐渐在协同控制、工程计算等各个领域得到广泛应用。多智能体系统分布式优化是通过多智能体之间的有效合作完成优化任务，在多智能体系统一致性的框架下求解分布式最优问题，其中有代表性的算法有基于迭代框架下的离散时间算法[5]、基于协调控制的连续时间算法[6]、基于有限时间收敛的不连续算法[7]和基于固定时间收敛的连续算法[8]。基于以上讨论，提出了一个求解多智能体优化问题的分布式指数时间收敛的算法。

1 预备知识和问题表述

1.1 代数图论

多智能体系统各智能体之间的通讯拓扑可以用图进行描述。令G={V,E,B} 表示一个拓扑图，其中V={v1,v2,…,vn} 表示其节点的集合，n为图中节点个数，节点的下标集合为In；E⊆V×V表示边的集合，eij=(vi,vj)表示图的边；邻接矩阵B=[bij]，其中bij为非负实数，表示节点vi到节点vj的连接权重。如果节点vi可以接收到节点vj的信息，则bij>0；否则，bij=0，假设相连节点之间连接权重均为1，拓扑图中每个节点没有自连，即对于所有i∈In，bij=0。如果一个拓扑图的邻接矩阵B是对称矩阵，则称该拓扑图是无向的。一个图的Laplacian 矩阵定义为L=[lij]∈Rn×n。当i=j时当i≠j时，lij=-bij。对于任意节点vi，定义其邻域节点集为Ni={vj∈V∶(vi,vj∈E)}。如果对于两个节点vi,vj，存在下标集合{k1,k2,…,ki} 满足，则称节点vi到节点vj之间存在一条有向信息传输路径。对于一个无向图，如果图中任意两个节点都存在至少一条有向连接路径，则称该图G是连通的。矩阵L所有特征根都是非负实数。矩阵L第二最小特征根λ2(L)>0，其又被称作该扑图的代数连通度，且因此，如果1Tε=0，则有εTLε≥λ2(L)εTε。

引理对于一个无向连通图的Laplacian 矩阵L具有如下的性质：

(1)0 是矩阵L的一个特征值，1 是其相应的特征向量；

(2)对任意向量ε=[ε1,ε2,…,εn]T，有下式成立

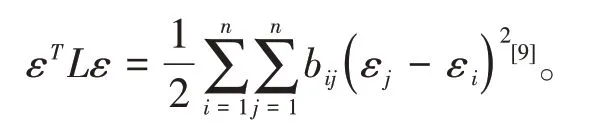
1.2 指数收敛

考虑方程

其中，f∶Rn→Rn为一个连续函数。

定义1方程(1)的解为有界的。如果对于任意的(t0,x0)∈R×Rn，都存在M=M(t0,x0)，使得对于一切t≥t0，有‖x(t0,x0)‖≤M[10]。

定义2方程(1)的解为全局指数收敛的。若存在正常数k,δ，使得任意解x(t)对唯一平衡解x0，当t≥t0时，有

1.3 问题表述

考虑由n个智能体组成的多智能体系统，其中每个智能体具有局部目标函数hi(xi)。要讨论的问题是在保持全局等式约束的同时，最小化所有局部目标函数的和，即

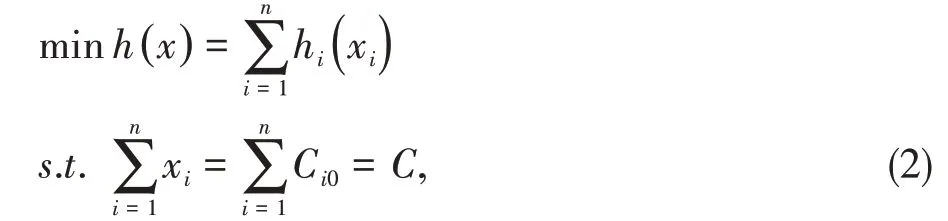
x=[x1,x2,…,xn]T是一个决策向量，h(x)是全局目标函数，hi(xi)是局部目标函数，Ci0表示变量，xi是一个常量。

注1问题(2)的等式约束来自一些物理约束，如资源配置、供需平衡、借贷平衡等。

假设1智能体之间的通信拓扑是无向连通图。

假设2目标函数hi(xi)是强凸的，存在正常数σ使得∇2hi(xi)≥σ>0。

由假设2可知问题(2)具有唯一的最优解。

2 指数时间收敛的算法设计

为求解优化问题(2)，提出下面的分布式算法：

其中，r是常数，yi和θi是辅助变量。事实上，根据假设1和bij=bji，则有

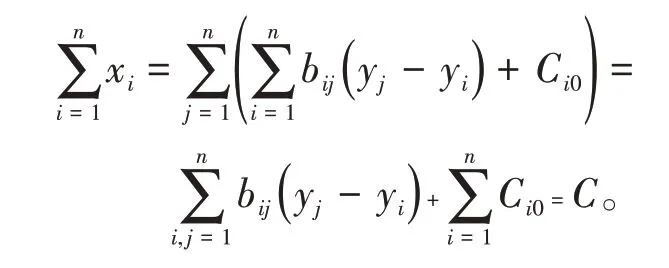
表示算法(3)始终满足问题(2)的等式约束，同时，将问题(2)转化为下面的无约束优化问题：

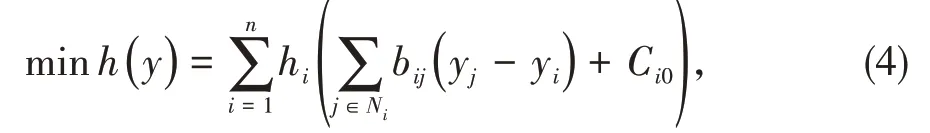
其中，y=[y1,y2,…,yn]T是辅助决策向量。

根据(3)式中的第二个式子，把xi(i=1,2,…,n)对yj(j=1,2,…,n)求导得

进一步，有

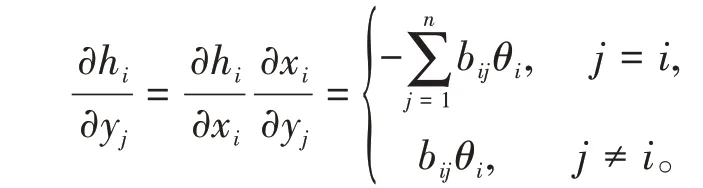
注意到h(x)的梯度为∇h(x)=(θ1,…,θn)T。

由(4)式，得到

其中，L代表通信图对应的拉普拉斯矩阵。显然，h(y)的Hessian矩阵满足

证明算法(3)的收敛性。

定理在假设1 和2 的条件下，分布式算法(3)可以在指数时间内求解问题(2)。

证明假设凸优化问题(2)的唯一最优解用z=[z1,z2,…,zn]T表示。a是任意常数，如果z=a1，则z是平凡解。探讨非平凡解的情况。对于任意的凸紧集Q⊂Rn/a1，和任意的y,w∈Q，由h(y)的强凸性可得

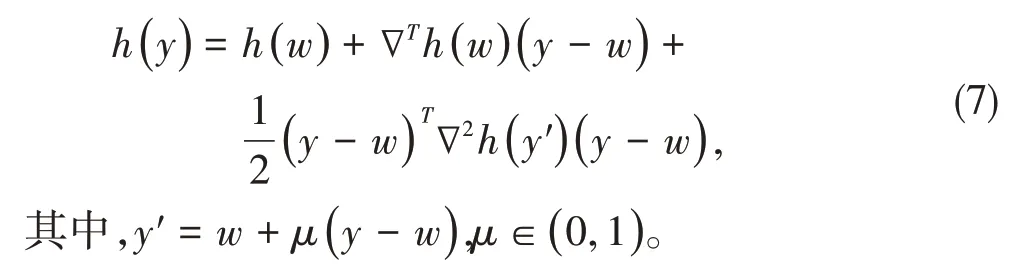
因为通信图是无向连通的，所以通信图拉普拉斯矩阵L特征向量1，ξ2,…,ξn的特征值相应的表示为0=λ1<λ2≤…≤λn，其 中‖ξi‖=1,i=2,…,n。向量y-z可以表示如下

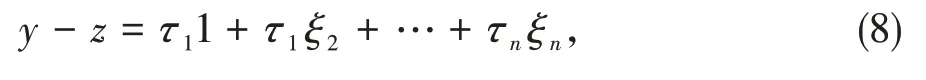
其中，τi(i=1,2,…,n)是常数，ξ=τ2ξ2+…+τn ξn，则

注意到

根据假设2，得

由(8)式，进一步得到

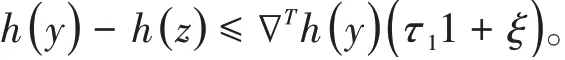
将(5)式代入上式的右边

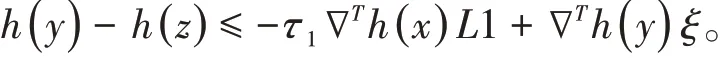
由于0 是拉普拉斯矩阵L特征向量1 的单特征值，则L1=0。因此

对于(7)式，设w=z。当∇h(z)=0，有

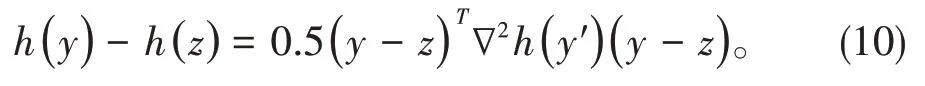
将(6)式代入(10)式得

根据假设2得

结合(9)和(11)有

注意，‖ξ‖≠0对非平凡解成立。因此

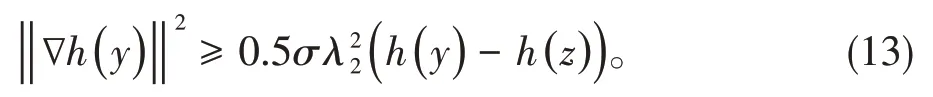
选取Lyapunov函数

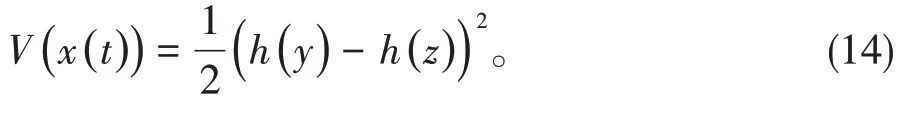
对(14)式求导得

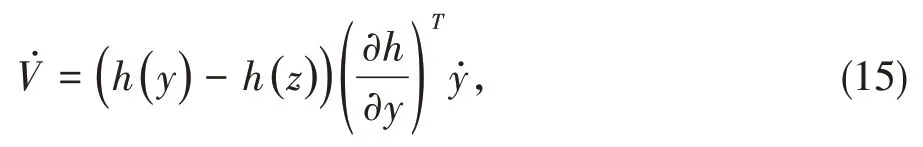
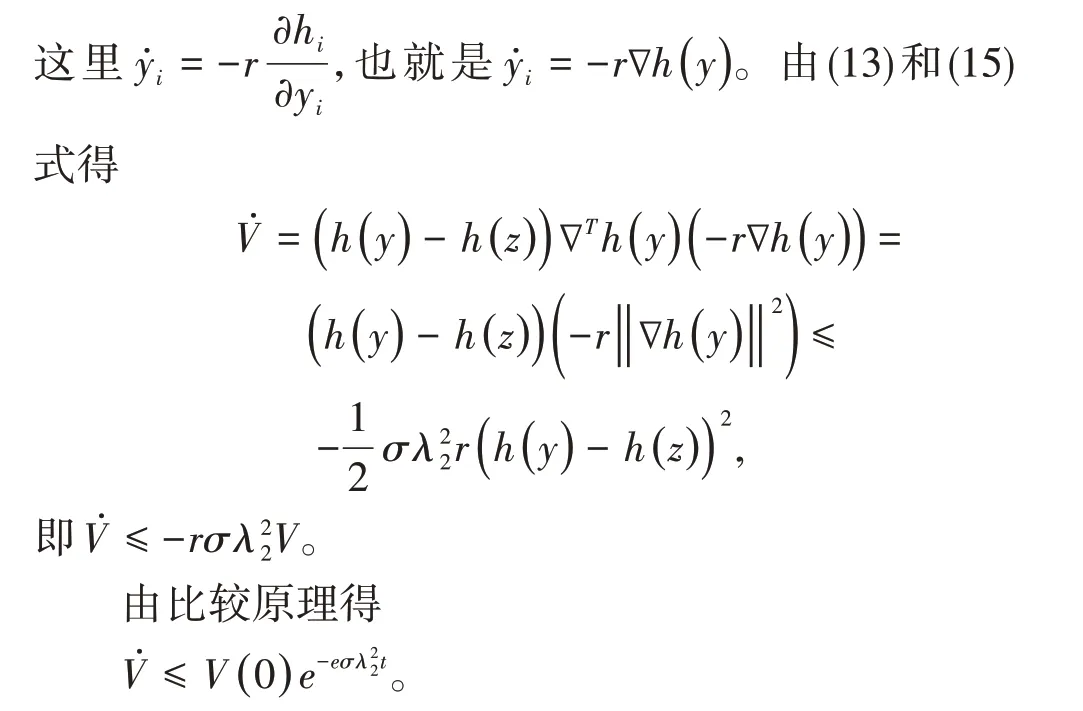
再由(10)式可得y指数收敛到z。即算法(3)在指数时间内能求解问题(2)。

3 数值模拟

用电力调度问题来测试算法(3)的性能。考虑一个由3 台发电机和3 个负载组成的电力系统，其中节点1、2、3 表示发电机，节点4、5、6 表示对应的负载，如图1所示。

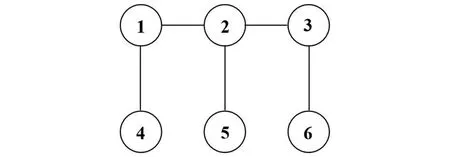
图1 电力系统

设xi(i=1,2,3)和C分别表示由第i台发电机产生的有效功功率和总负载需求。在电力工程中，发电机的成本函数hi(xi)一般由二次函数近似：hi(xi)=其中τi，βi和ηi代表成本系数。考虑的电力系统经济调度问题可以表达为

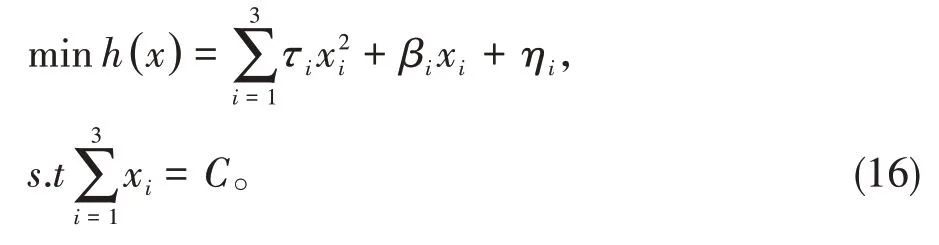
显然，算法(3)可以直接用于解决经济调度问题(16)。假设总负荷需求C为420 MW，成本系数τi，βi和ηi如表1所示。将初始状态设为

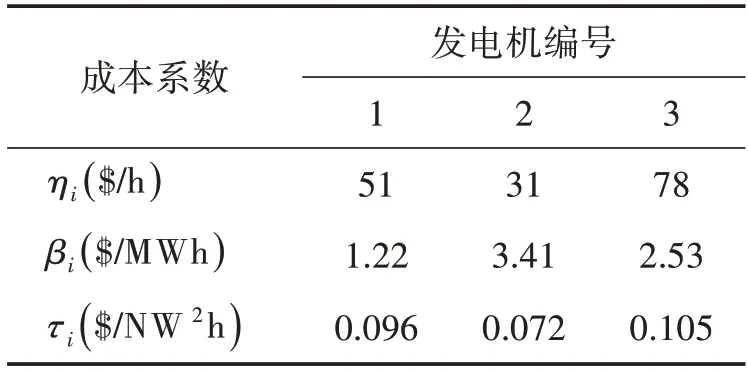
表1 发电机成本参数

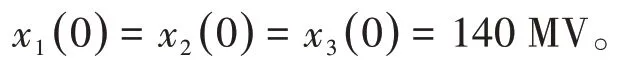
利用算法(3)得到的经济调度问题(16)解的动态轨迹，模拟结果显示最优解为

4 结语

对一类等式约束的分布凸优化问题，基于多智能体系统设计了一个指数时间收敛的算法，利用Lyapunov 函数理论，证明了算法的指数收敛性。最后通过实例模拟验证了理论分析的有效性。