基于改进的蜻蜓算法的特征选择

刘东强， 陈宏伟

(湖北工业大学计算机学院，湖北 武汉 430068)

近些年来，人们根据生物种群的各种行为，相继提出了各种各样的群体智能优化算法，并取得了诸多成果。例如遗传算法[1]，粒子群优化算法[2]，人工蜂群优化算法[3]，萤火虫算法[4]等。这些算法被研究者们很好的运用到了社会的各个领域。蜻蜓算法也是一种新颖的元启发式优化算法，它模拟蜻蜓的群体行为，是由Seyedali Mirjalili为解决连续优化问题在2015年提出的。蜻蜓算法被许多学者研究与运用，如崔学婷等人提出了一种混合改进蜻蜓算法并将其应用于特征选择[5]；文献[6]利用二进制蜻蜓算法设计了一种特征选择包装器，提高了特征选择分类效果；王万良等人为合理应用生产制造中产生的数据,分析和挖掘出数据中的关键特征和潜在信息,以帮助企业提高效率、降低成本,提出一种改进的蜻蜓算法,并将其用于特征选择[7]。为了提高蜻蜓算法的效率与精度，本文提出了一种改进的蜻蜓算法并运用于特征选择。文章在算法的种群初始化过程中引入混沌策略，并将原来的线性权重做了一个非线性调整，最终用具体的实验数据验证了改进后的蜻蜓算法的分类精度更好。

1 蜻蜓算法

蜻蜓算法是一种新的智群优化算法，该算法具有很强的分类搜索能力和迭代优化能力，已在各个领域得到了很好的应用。蜻蜓算法的主要灵感源于自然界中蜻蜓的群体行为[8]。蜻蜓有两个重要的群体行为：狩猎和迁徙。前者称为静态群体，后者称为动态群体。在静态群中，蜻蜓会成群结队，在一个小区域内来回飞行，以捕猎其他飞行的猎物，例如蝴蝶和蚊子[9]。在动态群中，大量的蜻蜓使群在一个方向上长距离迁移[10]。

基于蜻蜓的群体行为，建立了5个数学模型：

1)分离行为(Si)计算如下：

其中X是当前个体的位置，Xj表示第j个相邻个体的位置，n是相邻个体的数量。

2)对齐行为(Ai)计算如下：

其中Vj表示第j个相邻个体的速度，n是相邻个体的数量。

3)聚集行为(Ci)计算如下：

其中X是当前个体的位置，N是邻域的数目，Xj表示第j个邻域个体的位置。

4)觅食行为(Fi)计算如下：

Fi=X+-X

其中X是当前个体的位置，X+显示食物来源的位置。

5)避敌行为(Ei)计算如下：

Ei=X-+X

其中X是当前个人的位置，X-表示敌人的位置。

在进行蜻蜓个体位置更新时，首先计算步进矢量(ΔX)，步进矢量显示了蜻蜓的运动方向，并定义如下：

ΔXt+1=(sSi+aAi+cCi+fFi+eEi)+wΔXt

(1)

其中s、a、c、f和e为各自所对应的权重，Si、Ai和Ci分别表示个体的分离、对齐和凝聚力，Fi表示食物的吸引力，Ei表示敌人的影响力，w为惯性权重，t为迭代计数器。

计算步进矢量后，位置矢量的计算如下：

Xt+1=Xt+ΔXt+1

2 改进的蜻蜓算法

在本文中，提出了一种基于混沌理论的新的蜻蜓优化算法。普通的蜻蜓算法和其他许多智能优化算法一样，在迭代的过程中，很容易陷入局部最优的陷阱，而真正需要的是全局最优值。针对这一缺陷，本文在种群初始化的过程中加入混沌理论，得到覆盖面更广的初始种群。为了提高算法的收敛速度，对原蜻蜓算法中的惯性权重w做了一个非线性的调整，大大提高了算法效率与精度。算法的流程图见图1。

图 1 算法流程图

2.1 基于混沌策略初始化种群

本文中，为了提高初代蜻蜓种群的多样性，而不影响得到的结果，并为算法后期的全局搜索与迭代奠定良好的初始种群基础。本文在种群初始化的过程中，引用Tent混沌序列的逆混沌映射策略，得到一个品质更优的初代蜻蜓种群。

在本算法中，每个蜻蜓个体的维度为d，在初始化种群的时候，本文首先生成一个d维的蜻蜓个体 (i=1，2,…,n)，然后把生成的个体通过混沌映射，转化到另外一个解集中去，进而生成一个新的个体CXid(i=1，2,…,n)，计算方法如下：

式中Xid是第i个蜻蜓个体的第d维上的值，Xmind和Xmaxd分别是取值的下界和上界，种群CX={CXi,i=1,2,…,n}是通过混沌映射由种群X={Xi,i=1,2,…,n}变化得到。首先把X和CX两个种群合并成一个新的蜻蜓种群，其个体数为2n，然后再计算每个蜻蜓个体的适应值，并对得到的所有适应值进行排序，最后取前n个适应值所对应的蜻蜓个体来组成蜻蜓算法的初代种群。

2.2 惯性权重w的非线性改变

在原蜻蜓算法中，式(1)中的惯性权重w是一个线性变化的值，其计算方法见式(2)。在实际情况中，随着算法迭代次数的增加，算法收敛的速度会慢慢降低，是呈曲线下降的。算法中惯性权重w收敛的速度和算法整体的收敛速度不一致，这就会降低算法的收敛速度，从而影响算法的整体效率。

w=0.9-t(0.5/tmax)

(2)

式(2)中t为当前的迭代次数，tmax为开始设置的总迭代次数。从公式(2)中可以看出，随着迭代次数的增加，惯性权重w会呈直线趋势变小。在本文中，引用了指数递减策略，通过下面公式对惯性权重进行一个非线性的调整改变：

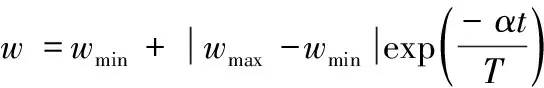
式中wmax和wmin分别为公式(2)中惯性权重w的最大值和最小值：wmax=0.9，wmin=0.4。其中α为调节系数，本文中取α=4，t和T分别为当前迭代次数和最大迭代次数。改进后的惯性权重w和原惯性权重w的对比图如图2所示，从图中可以看出改进后的w是呈曲线下降的，相对于原惯性权重w，其开始的变化速度很快，随着迭代次数的增加，变化的速度逐渐变慢，这能更好地适应算法的整体收敛速度。

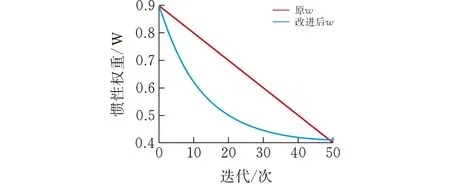
图 2 权重对比图

2.3 特征选择

特征选择是一种二进制优化问题，个体的位置都是由0或者1来表示。蜻蜓算法能够很好的解决连续优化问题，它通过将步长向量增加到位置向量的方法来改变个体的位置，但在二进制搜索空间中，种群个体的位置由0和1表示，此方法就不适用了。根据先前Mirjalili和Lewis的研究[11]。可以通过传递函数将连续优化算法转换成二进制算法，传递函数一般分为两种：S型和V型。本文采用V型传递函数，将原连续优化算法转换成了用于特征选择的二进制优化算法。

3 实验结果与分析

在实验中，本文先将改进后的二进制蜻蜓算法(CBDA)与原始的二进制蜻蜓算法(BDA)进行了比较，使用的数据集是两个UCI数据集：Wine和Sonar。本实验在Windows10操作系统下进行，电脑的相关配置：操作系统Windows 10, 64 bit，处理器Intel(R) Core(TM) i5-7200U，内存16 G，编程语言Python3.5.2。种群的规模都设置为30，迭代次数都设置为50。通过比较四种算法得到的最优个体的适应值来判断算法对于文本分类中特征选择的效果。

实验结果见图3、图4，从图中可以看出：改进后的二进制蜻蜓算法的收敛速度明显要好于原算法。

图 3 在Wine中函数适应度值

图 4 在Sonar中函数适应度值

为验证改进的蜻蜓算法性能，本文还将改进的二进制蜻蜓算法(CBDA)和传统的二进制遗传算法(BGA)、二进制粒子群算法(BPSO)进行比较。从30次运行结果中获取每种算法的平均分类精度，然后相互之间进行比较，得到表1的结果，从中可知改进后的蜻蜓算法的分类精度要好于其他算法。

表1 平均分类精度

4 结论

在本文中，将混沌映射和惯性权重的非线性改变运用到蜻蜓算法中，并将改进后的蜻蜓算法运用于特征选择来检验其效果。通过实验结果可以看出，改进后的蜻蜓算法的收敛速度相对于原算法得到了提高，而且相对于传统的优化算法，其分类精度也更高。