一种基于证据推理规则的集成学习方法
2021-08-24朱海龙曲媛媛杨文佳
朱海龙,徐 聪,曲媛媛,贺 维,3,杨文佳
1(哈尔滨师范大学 计算机科学与信息工程学院,哈尔滨 150500)
2(黑龙江农业工程职业学院,哈尔滨 150500)
3(中国人民解放军火箭军工程大学,西安 710025)
1 引 言
深度学习作为机器学习的一个分支,在数据挖掘、自然语言处理、推荐系统、目标追踪、图像识别等多个领域都取得了显著的成果,成为目前人工智能领域最受关注的技术.然而深层神经网络算法(Deep neural network algorithm,DNN)、卷积神经网络算法(Convolutional neural network algorithm,CNN)、递归神经网络算法(Recursive neural network algorithm,RNN)等深度学习领域的典型算法,在实际运用时受限于数据集的规模,有时难以提取到高精度的特征,使得模型无法达到预期效果.这时便需要对模型进行优化,当数据扩充等方式达到优化的瓶颈时,人们经常采用集成学习算法合并多个分类器的结果,降低泛化误差,提高最终模型的准确率.
集成学习由于其良好的泛化性能,一直以来都是学者研究的热点方向.文献[1]提出Bagging算法,该方法先采用有放回抽样的方式,产生多个数据集,之后通过基分类器训练模型,以简单多数投票法作为结合策略,将多个模型集成得到最终结果,该方法作为集成学习领域的典型算法,为集成学习后续的发展奠定了坚实的基础.文献[2]提出一种基于支持向量机的集成学习方法,该方法使用随机欠抽样与合成少数类过抽样技术结合的方式对数据集进行处理,形成多个数据子集,之后使用Boosting算法训练出多个基支持向量机的强分类器模型,通过投票法集成得到最终结果,该方法具有良好的检测性能.文献[3]提出了一种用于软件知识库挖掘的,基于进化规划的非对称加权最小二乘支持向量机集成学习方法,相比于其他分类算法可以有效提高精度.文献[4]提出了渐进式半监督集成学习方法,该方法在大多数数据集上都可以取得良好的表现,并在部分数据集上表现优越.文献[5]针对不同的标记源和非标记源,提出了一种集成学习算法,这种算法对于大型信息源具有更强的可扩展性,对于带噪声数据的标记源具有更强的鲁棒性.文献[6]在Bagging算法、AdaBoost算法、BRB(Belief Rule-Base)3者结合的基础上提出了基于梯度下降法的BRB系统的集成学习方法,该算法比单个BRB系统更为合理有效.文献[7]提出一种个性化加权的在线集成算法,该方法先将基分类器的权重与样本集的相似性进行关联,计算数据块之间的相似度,以该相似度为指标确定数据块对应基分类器的投票权重,再进行集成,该方法以在线的形式与无线传感器网络数据流进行了响应,相比传统的在线学习算法有更高的预测精度.以上文献都是近年来较为新颖的集成学习方法,然而这些方法在集成时大多采用平均法、投票法等表决融合方式作为结合策略,无法有效挖掘分类器的内部信息,不能明确地体现出各个分类器之间存在的关系,在多种分类器集成时无法将融合效果最大化.这种现象就像一个只能认知世界的婴儿,在拥有很多玩具时,无法通过自己的判断获得最好的搭配方案,需要大人的帮助进行决策.
人工智能是在研究模拟人类智能的基础上,衍生出的一门新的技术学科,集成学习作为该学科中重要的一个分支,也是在模拟人类思维方式的基础上建立起来的,它的集成过程便相当于人类的决策过程,因此也可以从决策的角度对集成学习的集成过程进行优化.Dempster-Shafer(D-S)证据理论作为智能决策领域的重要组成部分,利用Dempster规则进行证据融合,实现不确定性推理,具有很强的灵活性.然而该算法无法解决冲突证据,且存在指数爆炸等问题[8-10].
2013年,Yang等人建立了考虑证据权重和证据可靠度的ER规则,它明确区分了证据的可靠性和重要性,构成了一个通用的联合概率推理过程,可以有效地解决D-S证据推理中存在的问题[11,12].ER规则作为D-S理论的进一步发展,已经成为非经典推理领域的重要组成元素,并被成功应用于现代社会的各个行业中.文献[13]给出了基于ER规则的故障诊断方法,并使用该方法来解决不确定性故障特征信息的融合决策问题,该方法继承了D-S证据理论的优点,并克服了其无法区分证据可靠性和重要性的不足,可以使获得的诊断证据更为客观.文献[14]通过研究ER规则中证据权重归一化对合成结果的影响及ER规则与证据折扣方法之间的联系,在证据的重要性与可靠性表示上提出了一种改进方法.文献[15]提出了一种应用ER推理规则的多指标医学质量评价框架,将数据指标转换为定性等级,提高了不确定性条件下模型的鲁棒性.文献[16]提出一种基于数据可靠性和区间证据推理的故障检测方法,将专家知识与考虑可靠性的监测数据进行融合,提高了故障检测的准确性.文献[17]提出了一种扰动系数来表征ER规则的性能指标,分析了ER规则的鲁棒性和稳定性,为ER规则的研究运用提供理论依据和技术支持.
本文从智能决策的角度,采用ER规则作为集成学习中集成多种分类器时的结合策略,在集成过程中考虑了各个分类器之间实际存在的关联,克服了只考虑分类器数据间数值关系的集成学习算法的不足,并进一步提高了模型的准确率.在模型建模过程中,将分类器的预测结果视做ER规则中的证据,利用统计分析的方法设置证据的可靠度,运用熵权法代替专家知识来确定证据的权重,进一步增强模型参数设置的科学性.
文章结构如下:第1章对文章所解决问题的背景进行了概况描述;第2章从人的思维角度对集成学习的过程进行了分析与描述;第3章构建基于ER规则的集成学习模型,给出模型中证据的权重和可靠度的计算方法,并定义了模型的集成学习过程;第4章通过案例分析,验证了模型的有效性:第5章对全文进行了总结并提出今后工作的展望.
2 问题描述
人工智能是对人的意识、思维的一种延伸,它通过模拟人类基于智能创造出的理论、方法、技术,使得机器可以对客观世界产生类似于人类智能的反应,并对这种反应进行进一步的扩展[18].人工智能模拟人类行为的过程主要包括以下3个阶段:感知,认知,决策[19].具体实现如下:
1)智能感知阶段:机器设备智能感知外界事物,形成可以被算法处理的数据,将数据进行整理,形成数据集.假设v表示外界事物信息转换形成的数据集,例如图像、文本等类型数据.
2)智能认知阶段:数据集通过K种深度学习算法,形成K种分类器,称为智能认知模型.假设u(k)表示第k(k=1,…,K)种智能认知模型的认知结果.这个过程能够被描述为:
u(k)=fk(v,α)
(1)
其中,fk(·)表示第k种深度学习算法的认知过程,α表示认知过程中的参数集合.
3)智能决策阶段:将智能认知模型的认知结果通过相关策略进行集成,得到智能决策结果.假设u表示智能决策结果.这个过程能够被描述为:
u=g(u(k),β)
(2)
其中,g(·)表示智能决策的过程,β表示在决策过程中的参数集合.
集成学习可以认为是对问题的决策,通过对不同分类器的输出进行分析,获取最优输出结果.基于以上思想,通过人工智能模拟人类行为的过程来构建集成学习模型需要解决以下问题:
问题1.在构建集成学习方法时,从人类智能的角度描述集成学习过程.
问题2.在构建集成学习方法时,有效挖掘分类器内部和分类器之间的有效信息,进一步提高集成学习模型效果.
基于以上挑战,本文提出一种基于ER规则的集成学习方法.如图1所示.

图1 基于证据推理的集成学习模型
3 基于ER规则的集成学习模型
ER规则作为一种优秀的智能决策算法,在ER算法的基础上,新增了证据的可靠度属性,并融合到证据的置信分布中,通过ER规则可以更好地解决实际工程问题.
本文通过深度学习算法对机器感知世界形成的数据集进行处理,建立智能认知模型.将智能认知模型对于数据认知的结果作为证据,运用ER规则进行证据融合,构建智能决策模型,得到智能决策结果.在构建过程中,利用熵权法确定不同证据的权重,利用数理统计确定不同证据的可靠度.建模过程如图2所示.
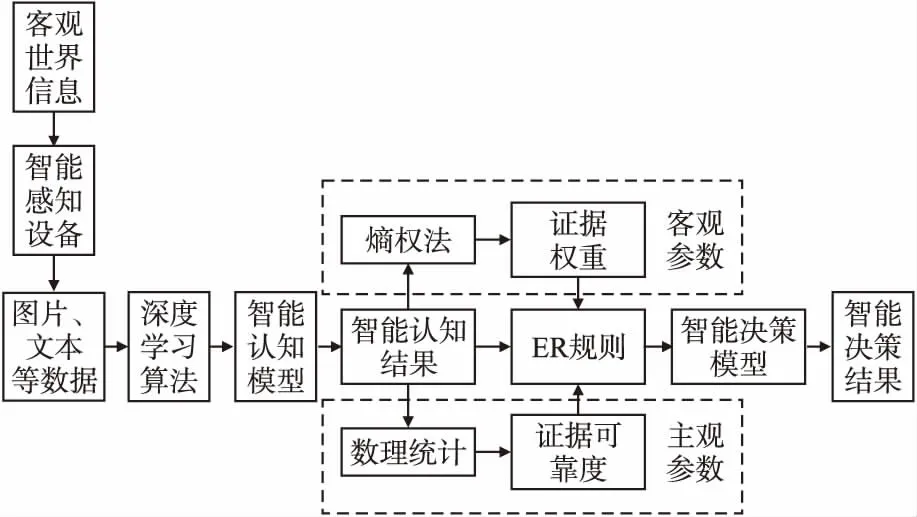
图2 集成学习模型的建模过程
3.1 集成模型的前期准备
通过传感器、摄像头等智能认知设备,将客观世界的信息转换成图片、文本等计算机可以处理的数据,将数据整理作为输入数据集,通过不同的深度学习算法提取数据的特征,经过训练得到智能认知模型.在训练过程中不断调整所使用的深度学习算法参数,提高智能认知模型的能力.
3.2 集成模型的构建
以智能认知结果为输入证据,通过ER规则进行融合,建立智能决策模型,在融合过程中通过熵权法等客观方法确定证据权重和证据可靠度,提高模型的决策能力.
3.2.1 证据权重
在传统的ER规则中,证据权重的设定通常由专家知识直接给出,然而专家知识具有主观性,且系统结构复杂时,无法给出精确的结果,这些问题同时也限制了ER规则在一些场景中的使用.
为提高决策模型的科学性,扩大其使用范围,本文采用熵权法代替专家知识来确定权重,熵权法作为一种基于数据的客观赋值方法,在系统情况复杂时,仍然可以通过数理分析的方法确定出精准的权重结果[20],已经被广泛运用于各个领域.在熵权法中,某个指标的信息熵EJ越大,它的离散程度越小,在综合评价中所起到的作用也越小,权重也越小[21].确定证据权重的过程如图3所示,步骤如下:

图3 证据权重计算过程
1)数据标准化
将机器感知信息形成的数据集v划分为训练集、测试集、预测集3部分.
以训练集与测试集为输入数据,通过深度学习算法建立智能认知模型u(k),以预测集为输入数据,通过智能认知模型得到智能认知结果x,作为原始指标矩阵中各个指标的数据,并进行标准化处理.假设有p个样本,K个智能认知模型,T种情况,则存在KT个指标X1,X2,…,XKT,其中Xj={x1j,x2j,……,xPj},xij为第i个样本的第j个指标数值(i=1,…,p;j=1,…,KT);本文中所使用的指标均为正向指标,通过Min-Max标准化得到:
(3)
2)计算上述正向指标的信息熵
第j个指标的信息熵为:
(4)
其中,
(5)
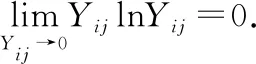
3)归一化确定上述正向指标的权重
由式(4)计算得出各组数据的信息熵为:
E1,E2,…,EKT
通过信息熵计算得:
(6)
(7)
其中,wkt为第kt个指标的权重,wk为第k个智能认知模型认知结果的权重,即ER规则中第k个证据的权重.
3.2.2 证据可靠度
证据可靠度由智能认知结果对应给出,如图4所示,流程如下:

图4 证据可靠度计算过程
以数据集v中的训练集与测试集为输入数据,通过深度学习算法建立智能认知模型u(k),以预测集为输入数据,通过智能认知模型得到智能认知结果,最终通过数理统计将智能认知结果转化为概率形式,作为该认知结果的证据可靠度,即ER规则中第k个证据的可靠度.
3.2.3 证据推理过程
1)假设集成过程中每个智能认知模型的认知结果为一个独立的证据,则共有K条独立证据ek(k=1,…,K).证据推理过程如图5所示.
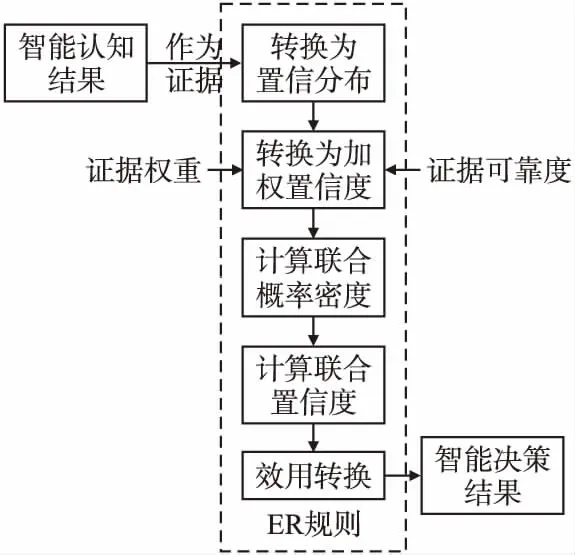
图5 证据推理过程
先将证据表示为置信分布,即第k个智能认知模型的认知结果ek可以被表示为:
ek={(θn,pn,k),n=1,…,N;(Θ,pΘ,k)}
(8)
其中θn(n=1,…,N)是评估等级.pn,k表示该评估方案在证据ek下被评估为θn的置信度,N为评估等级的个数.Θ={θ1,…,θN}为辨识框架,pΘ,k表示全局无知.
2)独立证据ek的权重为wk由3.2.1得出,可靠度为rk由3.2.2得出.带有可靠性的第k条证据的加权置信分布为:
(9)
其中,
(10)
(11)
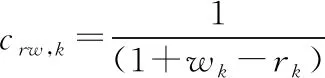
3)K条独立证据ek(k=1,…,K),对命题θ的Pθ,e(b)可以通过迭代下式得到:
∑A∩B=θmA,e(b-1)mB,b,∀θ⊆Θ
(12)
(13)
(14)
(15)
其中,k=1,…,L,mθ,e(1)=mθ,1,mP(Θ),e(1)=mP(Θ),1,mθ,e(b)为b条证据的联合概率密度,pθ,e(b)为b条证据的联合置信度.
4)设评估等级θn的效用为u(θn),决策模型的期望效用为:
(16)
4 案例分析
4.1 基于气象识别数据集的实验
本次实验所使用的数据集为GitHub平台上提供的天气图像公共数据包,内容为智能交通领域中某道路在不同天气情况下拍摄到的图片,按天气分为clear(484张)、cloudy(816张)、rain(648张)、snow(90张)4种情况,总计2038张图片.对于数据集中的每张图片采用Densenet、InceptionV3、Vgg16、Alexnet 4种深度学习算法进行预测分类,建立智能认知模型与智能决策模型,通过不同模型之间准确率的比较,验证该集成学习方法的有效性.具体实验步骤如下:
1)将数据集按6∶2∶2的比例划分为训练集、测试集、预测集,以训练集、测试集为输入数据导入到4种深度学习算法中,迭代优化产生4种智能认知模型.
2)将预测集导入到4种建立好的智能认知模型中,得出预测集中每张图片分别属于4种天气情况的概率,作为各智能认知模型的智能认知结果.
3)标准化智能认知结果,形成原始指标矩阵,通过熵权法计算得出证据权重.
4)对智能认知结果进行统计分析,得到各个智能认知模型的认知准确率,将准确率作为证据可靠度.
5)以智能认知结果为证据,以ER规则为结合策略,将4种智能认知模型的智能认知结果进行融合,形成决策模型,通过效用转换,计算准确率,即为智能决策结果.
本次实验所使用的4种深度学习算法在卷积层均采用RELU激活函数,并以全连接层接softmax函数作为输出层,在训练过程的超参数设置如表1所示.

表1 各模型的超参数
将预测集按clear、cloudy、rain、snow4种天气情况分类后,作为输入数据导入到智能认知模型与智能决策模型中,分别计算模型对不同天气情况下数据的预测准确率.
如表2及图6所示.基于ER规则的集成学习模型相比于单一的深度学习算法,在准确率方面有了明显的提升.
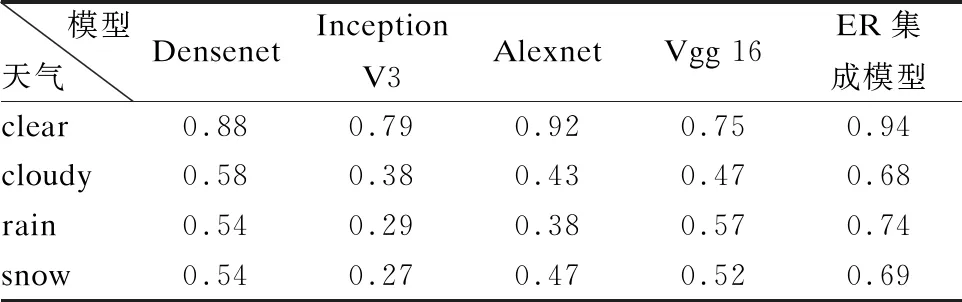
表2 不同天气情况下各模型准确率结果

图6 不同天气情况下各模型准确率对比
将数据集直接导入到不同模型中,得到总情况下各模型的准确率,如表3所示.在总体情况下,由ER规则进行集成后的集成模型比效果最好的深度学习算法在准确率方面依旧有2%-3%的有效提升.

表3 总情况下各模型准确率结果
仍以Densenet、InceptionV3、Alexnet、Vgg16这4种深度学习算法作为基分类器,采用不同的结合策略,对其形成的智能认知模型进行集成,准确率对比结果如表5所示.由ER规则作为结合策略的集成学习模型相比于其它集成学习模型有更高的准确率,基于熵权法的ER集成模型与基于专家知识的ER集成模型在准确率方面相近,但基于样本确定权重的熵权ER规则在融合多种分类器时,所设置的权重(如表4所示)更具科学性.

表4 不同ER规则的权重对比

表5 总情况下不同结合策略的集成模型准确率结果
4.2 基于花卉识别数据集的实验
本次实验所使用的数据集为百度AI Studio平台提供的公开数据集Flower中的部分数据集,包括daisy(633张)、dandelion(898张)、roses(641)、sunflowers(699张)4种,共计2871张图片,按训练集、测试集、预测集按6:2:2的比例进行划分.
将划分好的预测集作为输入数据,导入到InceptionV2、InceptionV3、Alexnet、Vgg16这4种深度学习算法建立的智能认知模型与ER集成模型中,预测准确率如表6所示.经过集成后的ER决策模型,相比单个模型,在准确率方面,有了一定的提高.

表6 各模型准确率结果
采用不同的结合策略对上述4种模型进行集成,集成后模型的准确率如表7所示,以ER规则为结合策略的集成模型相较其他方法效果更为优秀.
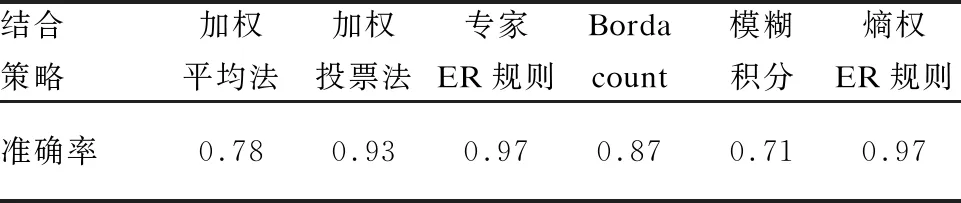
表7 不同结合策略的集成模型准确率结果
本文所用的方法,首先通过不同的深度学习算法分析训练数据,建立对应的智能认知模型,然后通过基于熵权法的ER规则将不同的智能认知模型进行集成形成智能决策模型,该方法符合人对事物的认知过程,最后将该方法分别运用于智能交通领域的气象识别及经典花卉识别任务中,通过准确率的提升证明了实验方法的有效性,并证明了该方法的泛化性能.
5 总结及展望
本文提出了一种基于ER规则的集成学习方法,丰富了集成学习领域的结合策略,并得到以下结论:
1)以ER规则作为结合策略的集成学习方法相比于使用其它结合策略的集成学习方法,其集成过程清晰透明,结果可追溯,并在准确率方面有了一定的提升.但该方法在基分类器为抽象级或排序级输出时,实用性还有待论证.
2)由熵权法设定权重的ER规则与由专家知识设定权重的ER规则相比,提供了精确的权重,不仅可以从统计分析的角度解释权重设立的合理性,提高模型的科学性,还可以应用于一些复杂情况中.此外,对于证据权重的设置还存在许多可以优化的地方,使其更为合理.
3)该方法适用于多种领域的分类任务,但在回归任务、目标追踪等方面的效果还有待验证.
