基于贪婪稀疏优化的欠定语音盲分离方法
2021-08-23杨璟安龙艳花
魏 爽,杨璟安,徐 朋,龙艳花
(上海师范大学 信息与机电工程学院,上海 200234)
0 引 言
欠定盲源分离(underdetermined blind source separation,UBSS)是一项用于盲信号处理的关键技术[1-6]。对于欠定盲源分离问题,混叠矩阵不可逆,无法通过混叠矩阵求逆来求解源信号,需要利用信号在变换域中的稀疏特征作为优化附加条件[7]。当前主要存在的欠定盲源分离方法是基于稀疏分量分析 (sparse component analysis,SCA)[8,9]的两步法,主要分为估计混叠矩阵阶段与恢复源信号阶段[10,11]。
在SCA的第一阶段,现有的方法采用势函数法[10]、聚类算法[12-14]、高阶统计估计量[15]等方法实现混叠矩阵的估计。其中,聚类算法更广泛地应用于变换域中具有稀疏性的源信号分离。但是,传统聚类算法容易存在陷入局部最优的问题。
在SCA的第二阶段,最短路径法[10]是最初用于恢复源信号的方法。但是,最短路径法仅适用于两路观测信号。当前对于多路观测信号,恢复源信号的方法主要分两类,一类是通过对近似L0范数的函数优化实现源信号的恢复,如:平滑L0范数(SL0)法[16-18],采用平滑连续函数近似L0范数。CTNRAL0方法[19]利用复合三角函数近似L0范数。这类算法对于源信号的来波方向较接近的情况恢复精度欠佳。另一类是采用压缩感知方法将L1范数优化代替L0范数优化实现源信号的恢复,避免了L0范数优化NP-hard问题。
通常情况下,语音信号在时域中的稀疏特征不明显。本文主要针对在频域中具有稀疏特征的语音信号,设计了一种基于贪婪稀疏优化的SCA两步法解决语音信号欠定盲分离问题。在估计混叠矩阵阶段,设计一种改进蚁群算法的K均值聚类算法,此方法在不具备先验知识的情况下实现自主聚类,解决传统聚类算法容易陷入局部最优的问题。在恢复源信号阶段,设计一种贪婪最优化思想逼近稀疏最优解,实现对语音源信号的恢复。该方法可以实现两路以上混叠信号的欠定盲分离,提高盲源信号来波方向比较接近情况下的信号恢复精度,保证了信号分离效率。
1 欠定盲源分离建模
1.1 欠定盲源分离数学模型
欠定盲源分离的数学模型如式(1)
X=A*S+E
(1)
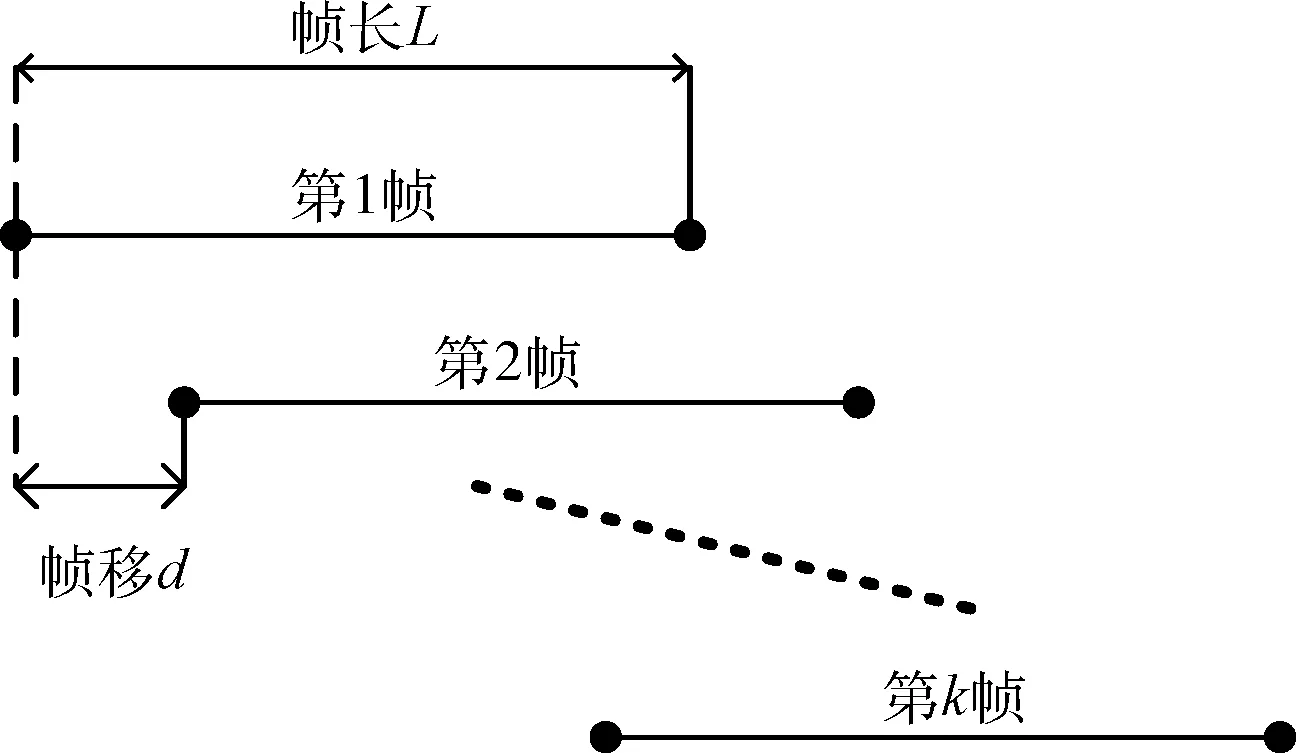
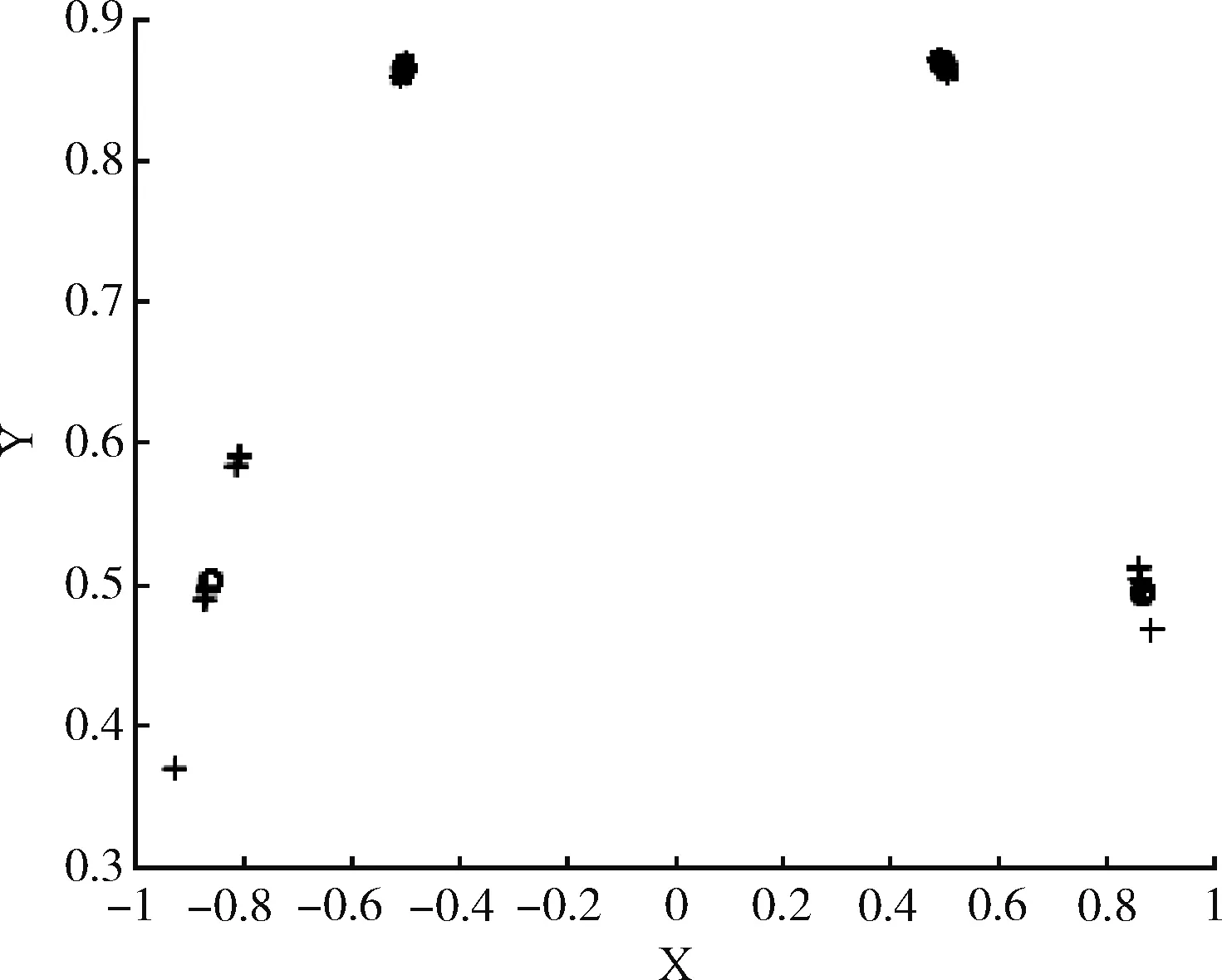
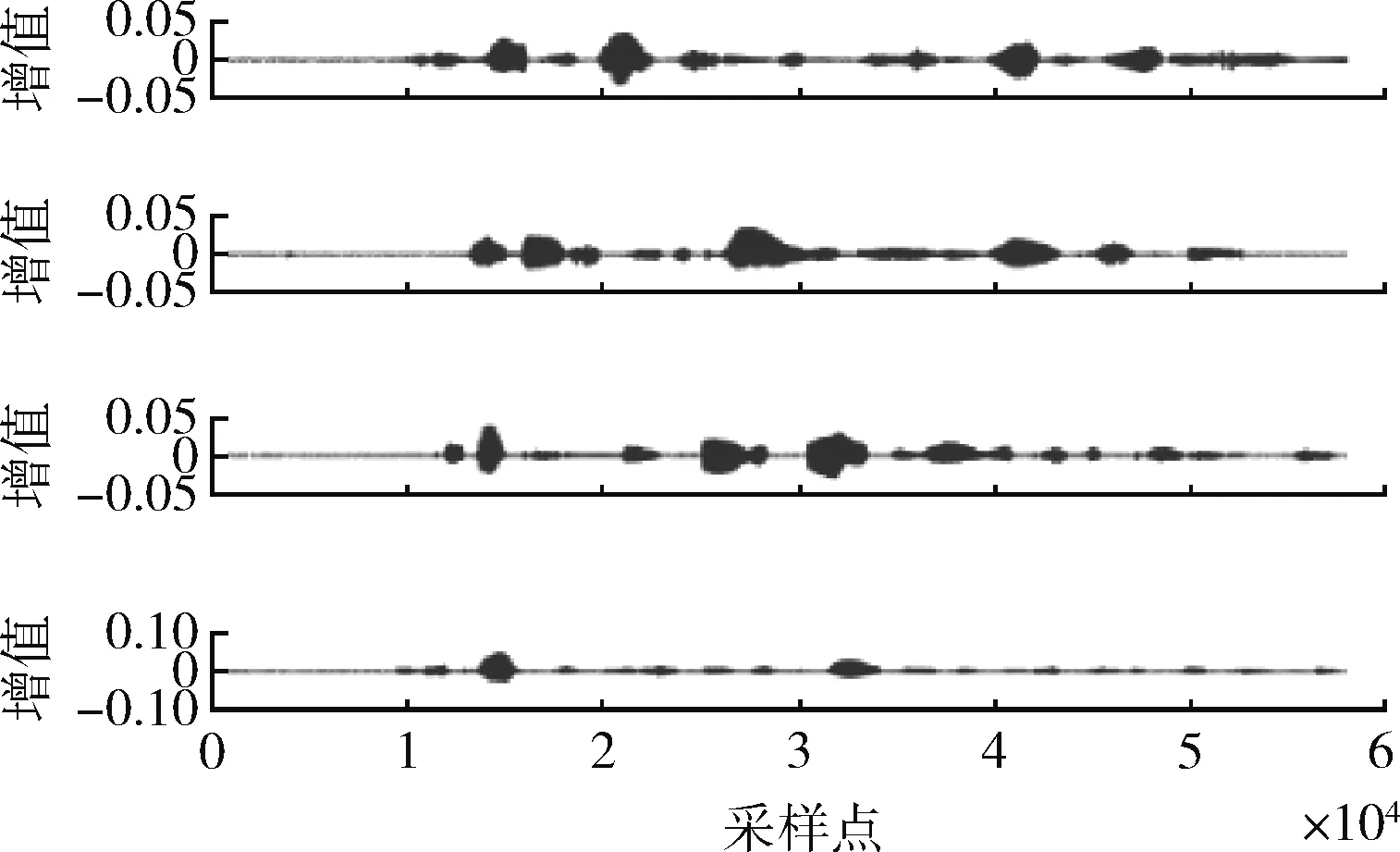
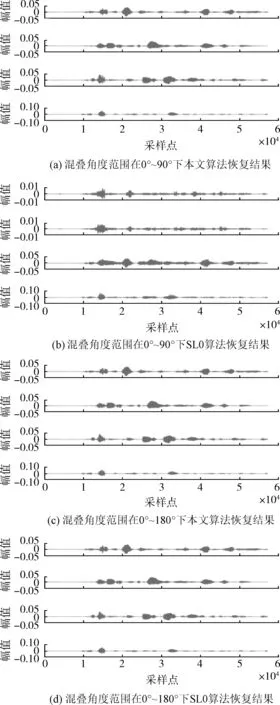
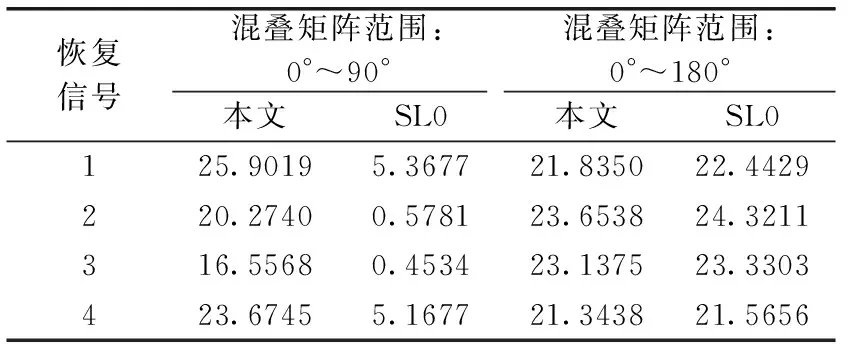
式中:S=[s1,s2,…,sn]T为n个源信号向量,每个源信号表示长度为l的向量si=[si(1),si(2),…,si(l)];X=[x1,x2,…,xm]T为接收的m个观测信号向量,其中,xi(t)=[xi(1),xi(2),…,xi(l)],A为m×n的混叠矩阵;E=[e1,e2,…,en]T为噪声信号。在欠定盲源分离模型下,观测信号的数量小于源信号的数量(m 一般来说,1.1中欠定模型问题下的解是不唯一的。不过,当该问题中加入解的稀疏特性作为约束条件时,则可以得到唯一的稀疏解。信号的稀疏性通常定义为单个信号中一部分点的取值不为零,而其余点的取值均为零或接近于零[20]。因此,获取语音源信号的稀疏特征,是求解欠定盲源分离问题的关键。 但是,一般情况下的语音信号在时域中的散点图是杂乱无章的,如图1所示。此时无法获取语音信号的稀疏特征,导致无法求解欠定问题。而语音信号在频域中的表征更具有稀疏特性。所以,首先需要对时域观测信号进行时频变换,将时域信号转换为频域信号,获取语音信号的稀疏特征。 图1 时域语音信号散点 图2 信号分帧处理 (2) 继续分别取出每个频域帧信号正半频谱的实部和虚部作为一种帧系数矩阵 (3) (4) (5) 图3 稀疏模型下语音信号散点 忽略噪声影响,将式(1)的时域模型转化为频域模型,如式(6)所示 (6) (7) (8) 图4 系统框架 蚁群算法是意大利学者Dorigo模拟蚂蚁觅食的原理设计出的一种集群智能算法[22]。蚂蚁觅食过程中会释放一种叫作信息素的分泌物,蚂蚁总是朝着更高信息素浓度方向移动。混叠矩阵的估计可以看成是蚂蚁沿着信息素寻找食物的过程。最终所有蚂蚁汇聚于相对于自己最优的食物点,形成若干个聚类中心,从而组成混叠矩阵A。 令预处理后的数据为Y,首先计算数据点之间的欧式距离,定义K均值优化准则。每个数据点i到其它数据点j的欧式距离如式(9)所示 (9) 式中:yk(i)表示i采样点第k个观测信号的数据,k的最大值为m,即观测信号的个数。 令蚂蚁从数据点i到数据点j的路径上产生的信息素为τij,则初始信息素矩阵定义为 (10) r为设定的阈值。dij≤r的数据被分为同一路径,对同一路径数据的坐标求解算数平均值,即得到了初始聚类中心C0。再利用式(9)计算每个数据点到初始聚类中心的距离即K均值优化准则函数 (11) 从而进一步利用式(11)计算结果更新数据到初始聚类中心的信息素,最终数据点根据转移概率进行聚类合并,转移概率如式(12) (12) (13) 式中:Yp(i)表示一个数据集合V(p)的第i个数据,g为V(p)中元素个数。 对于每只蚂蚁,将可行路径中所有数据点与不同聚类中心的欧式距离之和作为目标函数 (14) 式中:l为观测信号所有数据点的个数,p为各个聚类中心索引。 目标函数值越小,则聚类结果越紧凑。为了避免陷入局部最优解,本文利用变异操作在每次迭代中随机引入新的蚂蚁可行路径。计算变异后的临时聚类中心及相应的目标函数Ftemp。随后采取精英选择策略,比较原始目标函数值F与变异后的临时目标函数Ftemp,选取两者较小值作为新的目标函数值Fnew,将Fnew对应的可行路径作为最优路径,以此来得到全局最优解。随后计算新的聚类中心,重复迭代直至输出最优聚类中心Copt。 (15) 考虑到模型的欠定性与不同源信号之间的稀疏性, 本文使用贪婪最优化思想迭代寻找每个采样点的关键非零位置作为最优的源信号。 两个向量间的内积值表明了向量在方向上的接近程度,内积值越大则向量间的投影越大,相关性越大。本文算法以此为依据定义选择最优列原子的贪婪稀疏优化决策。最优列原子与观测信号相关性最高表明了在该采样点的所有源信号中,最优列原子位置对应的源信号的组成贡献值最大,则该位置对应的组成分量在源稀疏信号中具有非零值。组合每次迭代的最优解即得到了贪婪全局最优解。 在每次迭代选择结束之前,为了排除已选列原子对下次迭代选择的干扰,应从前一次的观测数据中减去已选列原子集合贡献的分量部分作为残差,如式(16)所示 (16) (17) 式中:n为混叠矩阵列数,与源信号数目相同。 本文所提方法依靠上述贪婪最优化思想,保证每次迭代中选择的原子都是最优的,从而减少迭代次数。因为迭代数与稀疏信号的非零数目相同,因此该算法具有工作量少,计算速度快,程序易于调试等优点。该方法能提高语音源信号的恢复性能,弥补了最短路径法和平滑L0范数法所存在的问题。 通过上述原理分析,本文所提的欠定盲源分离算法流程如下: 欠定盲源分离算法 (7)将所选列向量添加到增量矩阵 A_new=A_new∪Aj (8)使用最小二乘法计算源信号的近似值 在源信号稳定的情况下,可直接在频域内恢复源信号,再通过逆傅里叶变换将频域信号转换成时域源信号。 (3)每一帧乘以逆汉宁窗,两端各截去重叠部分的50%长度:(L-d)/2,保留每帧的中间部分; 在Matlab 2017b环境下使用两种不同类型的声信号进行仿真实验。其中,稳定声音源信号为来自于www.ac.upc.es/home/pau的六路长笛源信号,信号格式为.wav,采样点选择为35 000;不稳定语音源信号来自于TIMIT数据库的四路人声信号,信号格式为.wav,采样点选择为58 061。上述语音源信号分别经过六路混叠矩阵A1和四路混叠矩阵A2混合,形成两路观测信号,仿真实验中的混叠矩阵由人为设定,分别为 A1= 采用本文算法,进行欠定盲源分离,以分离后恢复信号的信噪比SNR为评价指标。具体实验及结果分析如下。 经过六路混叠矩阵A1获得的两路笛声观测信号如图5所示。对观测信号进行傅里叶变换,采用改进蚁群聚类算法得到的聚类结果如图6所示。图中6个聚类中心坐标分别代表了混叠矩阵的6个列向量。混叠矩阵估计结果如下 图5 两路笛声混叠信号 图6 六路笛声源信号蚁群聚类结果 在两步法第二步恢复源信号实验中,将本文所提恢复算法与SL0恢复算法进行仿真对比。SL0算法求解过程中采用的步长μ=2,平滑L0函数的σ下降因子σdecrease_factor=0.5,迭代阈值σmin=0.001。分别讨论了混叠矩阵列向量角度分布于0°~90°和0°~180°两种不同范围内的恢复效果。在相同数目源信号前提下,混叠矩阵列向量的角度分布范围越小表示不同源信号的来波方向接近。图7为六路长笛源信号。图8(a)、图8(b)分别为本文算法与SL0算法在混叠矩阵列向量角度分布于0°~90°范围内的源信号恢复结果。图8(c)、图8(d)分别为本文算法与SL0算法在混叠矩阵列向量角度分布于0°~180°范围内的源信号恢复结果。表1给出了这两种方法在不同混叠角度范围的六路恢复信号SNR结果。 表1 六路笛声恢复信号的SNR指标对比 图7 六路笛声源信号 图8 六路笛声不同混叠角度范围下的恢复结果对比 经过四路混叠矩阵A2获得的两路人声语音观测信号如图9所示。对观测信号进行短时傅里叶变换,分帧帧长为2048个采样点,帧移为614个采样点。采用改进蚁群聚类算法得到的聚类结果如图10所示。图中4个聚类中心分别代表了混叠矩阵的4个列向量。混叠矩阵估计结果如下 图9 两路语音混叠信号 图10 四路语音信号蚁群聚类结果 四路语音源信号如图11所示。图12(a)、图12(b)分别为本文算法与SL0算法在混叠矩阵列向量角度分布于0°~90°范围内的恢复结果。图12(c)、图12(d)分别为本文算法与SL0算法在混叠矩阵列向量角度分布于0°~180°范围内的恢复结果。表2给出了这两种方法在不同混叠角度范围的四路恢复源信号SNR结果。 图11 四路人声源信号 图12 四路人声不同混叠角度范围下的恢复结果对比 表2 四路语音恢复信号的SNR指标对比 为了验证本文所提方法可以突破最短路径法只能恢复两路观测信号的局限性。本实验使用三路观测信号情况下的六路笛声源信号进行欠定盲源分离,混叠矩阵设定为 A= 恢复结果如图13所示,恢复信号的SNR指标见表3。通过恢复结果图与SNR指标可以看到:该方法可以成功恢复六路笛声,实现了三路观测信号的欠定盲源分离。 表3 三路观测信号六路笛声恢复信号的SNR指标 图13 六路笛声三路观测信号恢复结果 通过3.1节与3.2节的仿真实验结果可见:本文所提算法可以精确估计欠定混叠矩阵。当混叠矩阵列向量角度分布范围在0°~90°时,无论是稳定的笛声源信号还是不稳定的人声语音源信号,SL0范数恢复源信号的效果都欠佳,而本文方法仍然适用。当混叠矩阵列向量角度分布范围在0°~180°时,本文方法与SL0算法恢复结果相近,恢复信号都具有较高的SNR指标。由此可知本文方法的应用范围更广,更符合实际情况。表1的SNR指标普遍低于表2,这主要由于不稳定语音源信号的高复杂性以及在获取稀疏特征采取了短时处理和信号恢复重构后处理等原因造成的。3.3节的仿真实验验证了本文算法不仅适用于两路观测信号的情况,而且适用于多通道数的观测信号情况下的源信号恢复。 本文主要研究一种基于贪婪稀疏优化的语音信号欠定盲分离方法。在稀疏分量分析方法的第一步采用改进蚁群算法的K均值聚类算法对欠定混叠矩阵进行估计。第二步将贪婪最优化思想与稀疏分量分析方法相结合恢复语音源信号。实验结果表明,本文方法使用范围更广,可以较准确地从多通道观测信号中恢复信号,可以有效提高来波方向较近的语音盲信号分离性能。考虑到在恢复不稳定源信号时,由于获取信号稀疏特征时的短时分析和信号恢复时重构后处理等原因造成的误差。下一步的研究中将通过算法的改进进一步提高不稳定源信号的恢复性能。1.2 语音信号在变换域中的稀疏特征获取



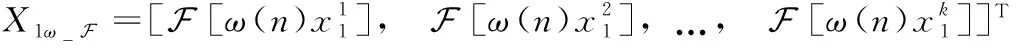




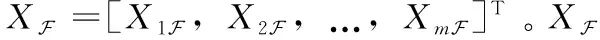


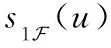

2 欠定盲源分离两步法
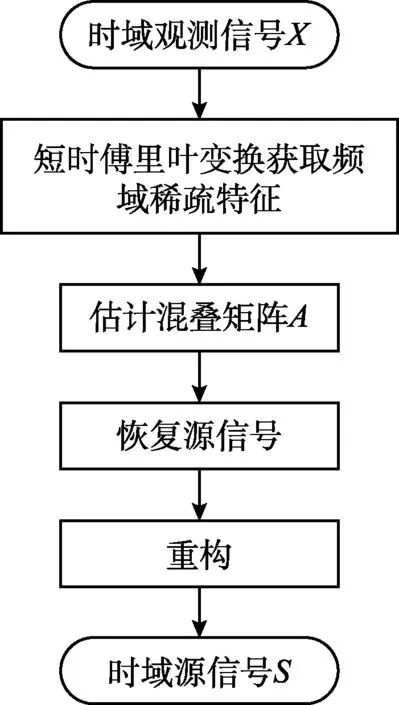
2.1 混叠矩阵估计原理
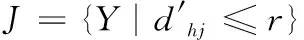

2.2 源信号恢复原理


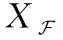


2.3 欠定盲源分离算法步骤
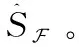
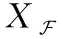
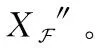
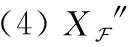

2.4 重构时域语音源信号


3 仿真实验及结果分析

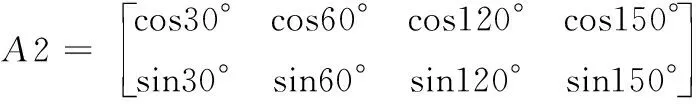
3.1 六路长笛信号欠定盲源分离

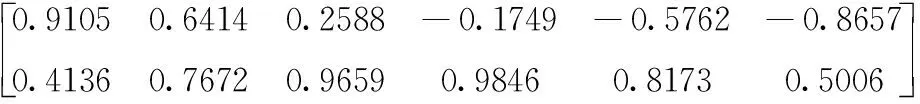



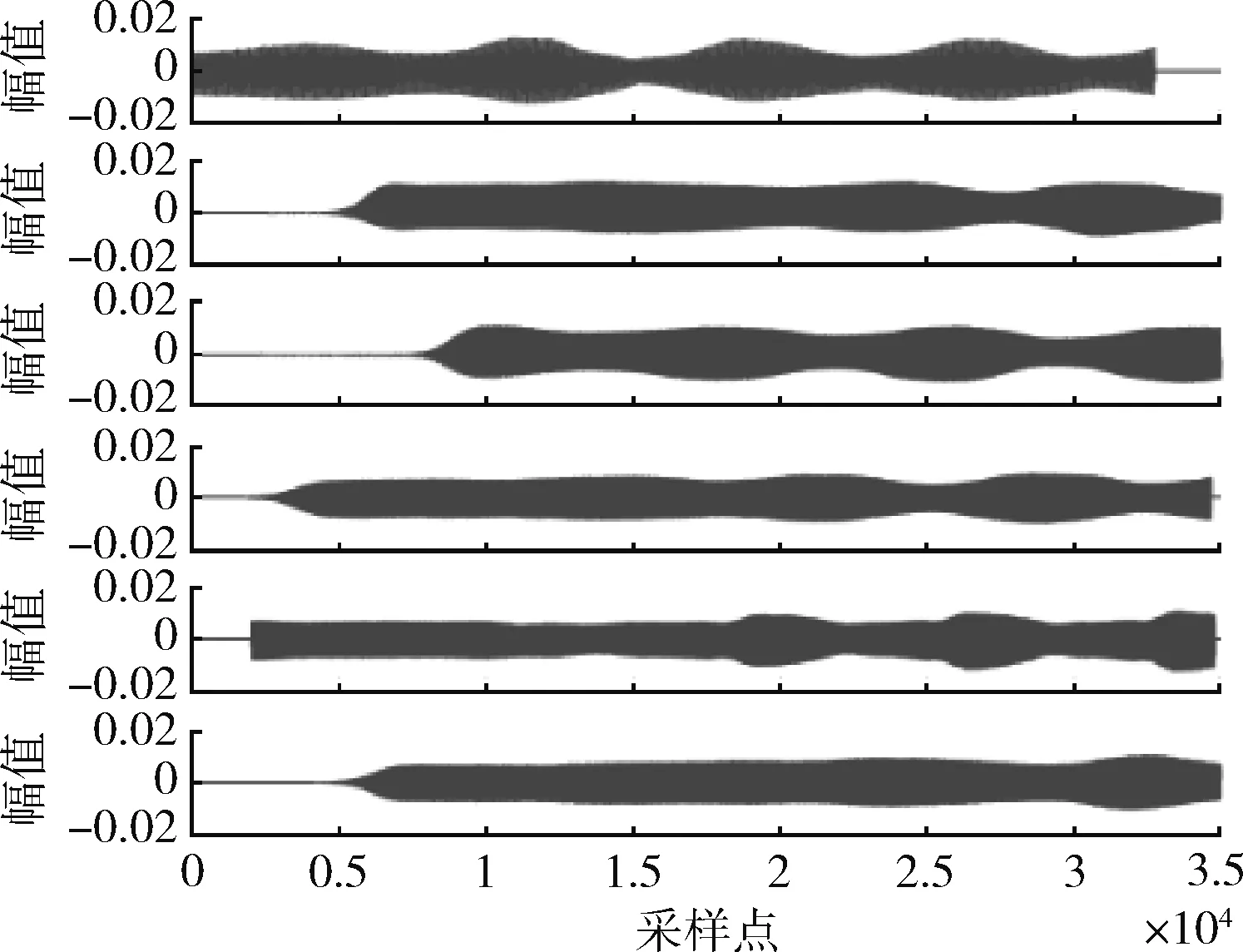

3.2 四路人声信号欠定盲源分离
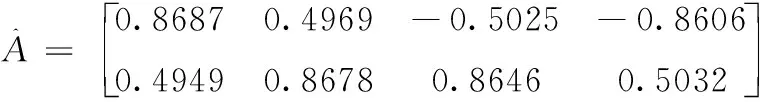

3.3 三路观测信号欠定盲源分离



4 结束语
