基于双哈希模糊布隆滤波器云存储数据融合
2021-08-23洪文圳李冬睿
洪文圳,李冬睿,沈 阳
(1.广东农工商职业技术学院 计算机学院,广东 广州 510507; 2.华南理工大学 软件学院,广东 广州 510641)
0 引 言
工业物联网(IIoT)在各领域的应用越来越多,IIoT连接传感器和执行器快速大量生成异构数据[1,2]。当前面临挑战是高效和安全地存储和处理/分析大量数据,特别是敏感IIoT数据[3,4]。此外,流式数据可能是短暂的,因此需要能够在一次传输中对此类数据进行及时的分析和处理[5]。
当前已有许多针对IIoT数据的处理方法,例如,熊等。文献[6]设计了一种近似的基于Bloom滤波器的密钥值(k-v)存储方法。文献[7]提出一种动态Bloom滤波器数组,用于云存储系统中成员身份的有效表示。文献[8]提出可调节Bloom过滤器,称为Scalable Bloom滤波器(SBF),通过添加新的过滤器来执行批量数据的插入,并且在两个不同级别上执行查询处理以提高其准确性和查询复杂度。文献[9]提出基于SDN的大数据管理方法来优化多云DT中的网络资源消耗,Bloom滤波器被用来分析他们提出的解决方案的性能。Bloom滤波器在各个领域广泛应用,可有效地处理可扩展性问题,缺点是查询复杂度随着输入数据量增加而增加。
本文提出一种在确保失效数据鲁棒性条件下,将两个Bloom滤波器压缩成一个滤波器的新方法,可更为有效利用存储容量:①使用模糊交叉操作压缩合并两个Bloom滤波器,大量元素被容纳在m大小Bloom滤波器中;②数据缓慢衰减,允许流数据在内存中驻留相当长的时间;③在不损失精度的情况下高效优化利用存储空间。
1 数据存储系统模型描述
1.1 IIoT网络结构模型
图1描绘了包括不同层的典型IIoT网络结构设置,这些层结构的主要作用是信息获取、计算、存储和检索。在初始阶段,从地理分布的传感器和执行器获取异构数据。然后,通过IIoT和Internet基础设施将收集的数据传送到地理上分布的云DCs中,在那里存储和深入分析数据。数据分析的结果随后提供给授权用户(例如,通过移动设备)。
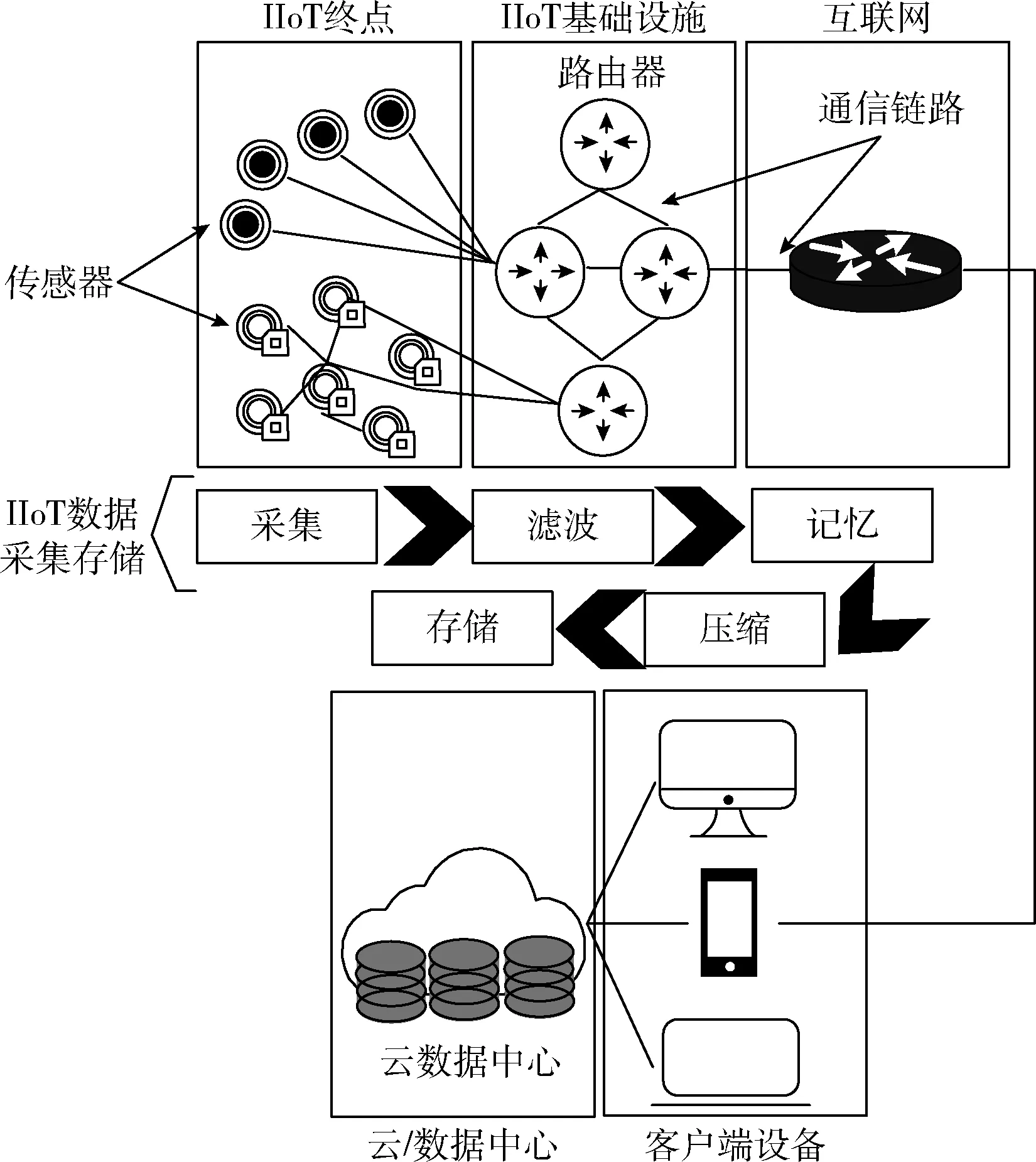
图1 IIoT环境下的数据存储
典型的IIoT环境中的数据存储包含以下两个阶段:①数据从连接设备、传感器以及执行器进行发送;②一旦收到数据,对其进行滤波以去除异常和冗余值,并将过滤后的数据保存在内存中,直到在主内存中找到足够存储空间。与数据存储相关的重要任务是明确数据压缩(例如,在不影响其准确性的情况下,将减少的数据保存在较小的内存空间中)。目的是研究数据压缩,以确保有效地利用可用的存储空间进行大规模数据存储。
1.2 Bloom滤波器
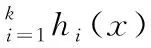
fp≈(1-e-kn/m)k
(1)
假阳性率可能随着Bloom滤波器中潜在的插入过程而增加。然而,Bloom滤波器固有的节省空间的能力,往往克服了这一缺点。
1.3 问题描述
给定具有n个元素的数据流(Ds),即Ds={x1,x2,…,xn},主要要求是在存储器和搜索复杂度方面改进现有的Bloom滤波器的性能。所设计结构可表示为如下问题[13]:
(1)流数据在很短时间内是可用的,因此必须一次性处理,并在内存中保留足够长时间以便查询。
(2)与散列相关的计算成本(Cc)应最小化。
(3)处理动态数据集时的查询复杂性(Qc)应得到优化。
(4)用于存储数据的存储器应以最大数量的元素可容纳的方式进行优化(Ea)。
(5)假阳性(fp),Bloom滤波器的重要性能参数不应超过预定限值。
上述问题可表示为如下数学模型
(2)
2 模糊交叉Bloom滤波器(FFBF)
2.1 模糊交叉操作
模糊交叉操作[14],首先合并ax∈BFi[]和by∈BFj[]的元素,其中x=y。这两个元素在两部分中具有相同的索引,彼此重叠并在上半部分存储为单个模糊值。在此过程中,指纹位用于数据压缩。融合的两个Bloom滤波器,BFi[]和BFj[],被称为第一交叉或第一压缩形式。它由符号CRi,j表示,并且需要两个位(块位和指纹位)来表示使用模糊符号存储在其中的元素。模糊交叉操作表示为⊙,并表示为如下模型
(3)

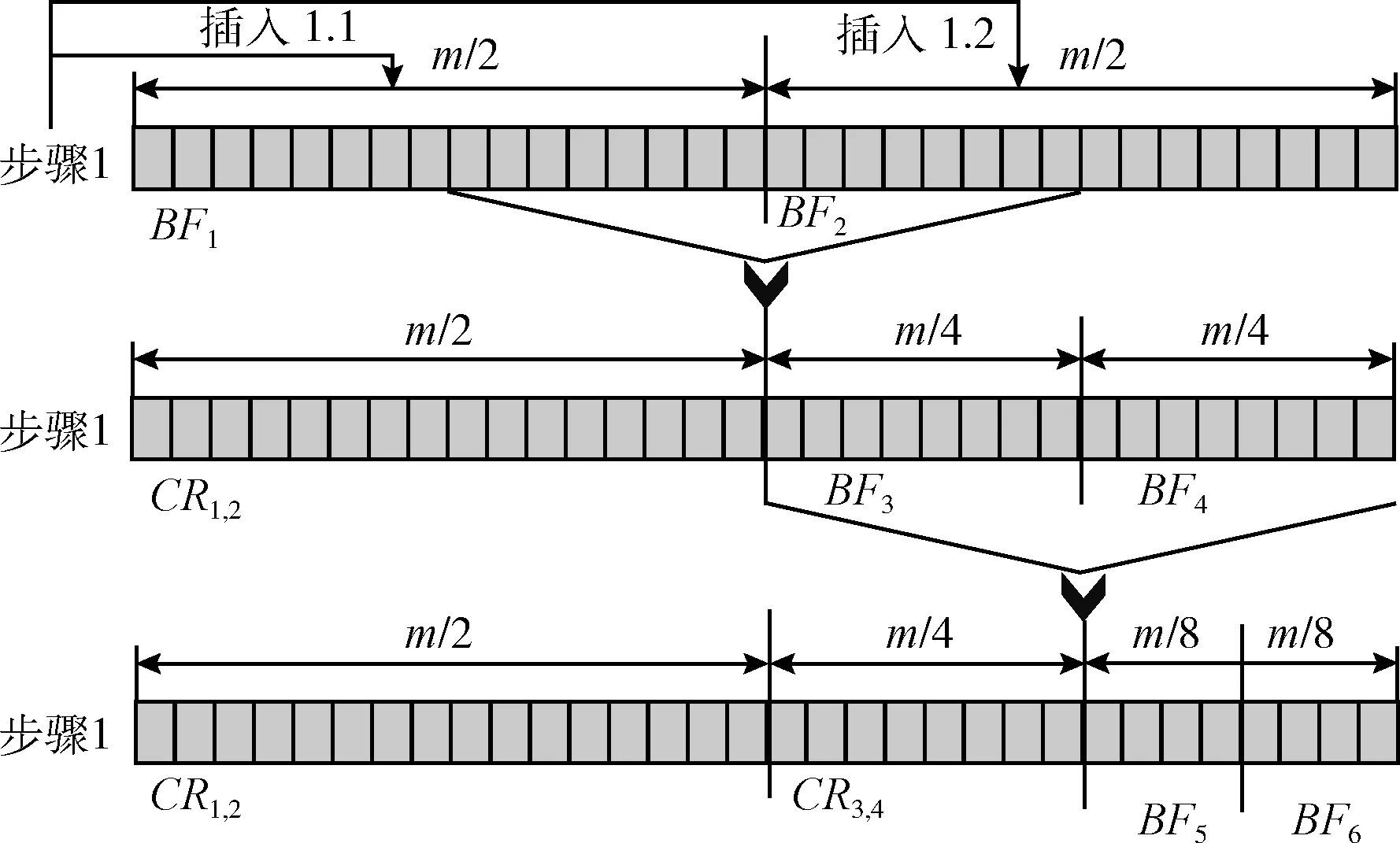
图2 模糊交叉过程
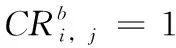
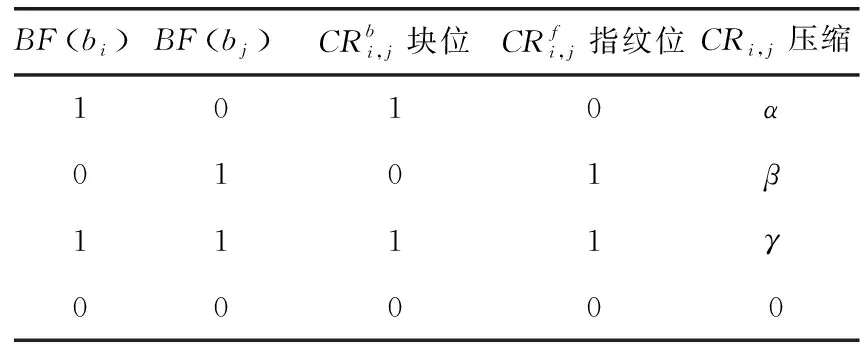
表1 模糊操作
初始阶段数据m/2,m/4,m/8,…可以压缩形式查询。简单Bloom滤波器的主要特点是具有几乎立即衰减率,FFBF与之相比具有相对较慢的衰减过程。FFBF中采用的交叉操作的计算成本几乎可忽略,因为它仅对二进制集应用简单的模糊操作。此外,当m取值较小时,所提模糊交叉操作在计算上变得低效。在这种情况下,通过将所有比特位设置为零可获得相对更高的计算效率。
定理1模糊交叉运算不可交换,即
(BFi[]⊙BFj[])≠(BFj[]⊙BFi[])
(4)
证明:在FFBF算法中,Bloom滤波器的位置在交叉操作中起着重要作用。根据式(3),CR1,2是指BF1和BF2的压缩形式。CR1,2中元素qy的查询过程表示如下
(5)
因此,在模糊操作中Bloom滤波器的位置发生变化,搜索结果将受到重大影响。可以得出结论,模糊交叉运算不可交换
CR1,2≠CR2,1
(BFi[]⊙BFj[])≠(BFj[]⊙BFi[])
(6)
对于上述引理,得出结论如下:在模糊交叉运算中,α和β是互补的,而γ独立于Bloom滤波器的位置。
定理2对于具有m和k哈希函数数组的给定Bloom滤波器,由FFBF容纳的元素数(NFFBF)是简单Bloom滤波器(SBF)容纳的元素数(NSBF)的1.9倍
NFFBF≈1.9×(NSBF)
(7)

(8)
总迭代次数k由b个块表示,如下所示
(9)
对于给定的m大小的Bloom滤波器,与SBE相比FFBF中可用的总内存(MFFBF)可计算如下
(10)
(11)
假设n个元素可由使用m大小Bloom滤波器的SBF容纳。在相同大小数组中,FFBF可容纳的元素总数如下所示
(12)

(13)
定理3CRi,i+1压缩表示的假阳性率(FPCR)等于BFi[]和BFi+1[]的假阳性率(即FPi和FPi+1)
(14)
证明:模糊折叠是一种算术运算,CRi,i+1中的单个元素(即,来自BFi[]和BFi+1[]的个数)用模糊符号α,β,γ表示。每个符号都有唯一的签名,见表1。例如,BFj[]中α表示1,而在BFj[]中α表示0。CRi,i+1的误差主要来自于BFi[]和BFi+1[]中的突变位。但是,使用模糊符号不会导致CRi,i+1出现误差。
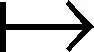
(15)
因此,压缩表示的假阳性率与具有参数m和k的SBF假阳性率相同。
2.2 FFBF中的数据插入
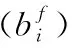
gi(x)={h1(x)+i×h2(x)}modmp
(16)
在上面公式中,mp是相对于BF(m)大小的最大限制范围(1:m)和最接近素数(减少冲突次数)之间的散列函数的值。mp的选择采取可生成最佳散列值方式进行选取。插入首先将m大小的数组划分为两个相同大小的Bloom滤波器
(17)
最初,元素被添加到第i个Bloom滤波器中。然而,当BFi[]的填充容量超过阈值填充比(Fthres)时,插入从BFi+1[]开始。在插入的第一级,根据以下散列值,只有块位被设置为1
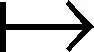
(18)
一旦达到BFi+1[]滤波器的阈值,模糊交叉操作⊙被应用在两个滤波器(BFi[]和BFi+1[])上,以便在现有的Bloom滤波器中为更多的数据存储空间。为使模糊交叉操作有效,m和k应该是2的倍数(即,表示为2x)。具体计算过程见算法1所示。
算法1:FFBF中的数据插入过程
输入:数据流(S)
输出:Bloom滤波器操作—插入&&折叠
(1) 设置S(Bloom滤波器的数据集);
(2) 设置m←Bloom滤波器的大小;
(3) 设置k←哈希函数(2x);
(4) 设置i←1;
(5) 设置BF[i]←Size(1,m/2);
(6) 设置BF[i+1]←Size(m/2+1,m);
(7) forx∈Sdo
(8) ifm≥kdo
(9) if FillRatio(BFi[])>Fthresthen
(10) if FillRatio(BFi+1[])>Fthresthen

(12)BFi[]←Size(1,m/2);BFi+1[]←Size(m/2+1,m);
(13) endif
(14) else


(17) endfor
(18) end
(19) endif
(20) else


(23) endfor
(24) end
(25) endif
(26) else
(27) 达到最大插入极限;
(28) end
(29) end
2.3 FFBF中的数据查询
FFBF中的查询过程与标准Bloom滤波器的相同,这表明查询的数据最初是散列的,Bloom滤波器中的相应位置被扫描以获取HIGH位。在FFBF中,查询过程始终从活动时隙A开始。如果在第A个时隙中找到元素,则查询过程返回TRUE;否则,扫描将继续,直到A=1搜索开始,按如下散列查询方式
(19)

(20)
下面是根据上面定义的hResult()函数得出的结论
(21)
根据以上讨论可得,查询CR中的一个项目(y∈Q)的时间复杂度是O(k),如果CRi,i+1表示时隙BF[i]和BF[i+1]的2n个元素。算法2描述了上述FFBF中使用的整个查询过程。
算法2:FFBF中的数据查询过程
输入:数据流(S)
输出:Bloom滤波器操作—插入&&折叠
(1) 设置a←insertion(i);
(2) whilea≠0 do
(3) ifa→(BF[a]) then

(5)y∈BF[a]th;
(6) endif
(7) endif
(8) else ifa→(CRa-1,a) then
(9) Update(Cα,Cβ,Cγ)←hResult(y);

(11) endif
(12) if memPa==1 then
(13)y∈BFa-1[]th;
(14) endif
(15) else if memPa-1==1&&memPa==1 then
(16)y∈BFa[]th&&BFa-1[]th;
(17) end
(18) endif
(19)a=a-1;
(20) end
(21)y∉S;
3 实验分析
为实现对所提云存储数据融合算法的性能测试,本实验选取PBC 0.5.15测试库进行模拟测试,可实现对文件失效情况下的批量审计模型设计,同时选取文献[13-15]这3种云存储算法进行对比实验,该测试系统选取的开发语言是C语言。测试系统平台软件选取Linux 3.8.0-29,处理器配置为CPU Intel(R) E5605@2.55 GHz,系统内存大小是32 GB,系统硬盘是1 TB希捷机械硬盘。
设置云存储过程中的数据块大小是|id|=50 b,云存储过程的测试文件大小为1 GB,设定模拟测试过程中的文件损坏的最大比例是1%,选取所有数据块中的500组作为模拟对象进行数据审计。实验对比指标首先选取云存储过程中的通信数据开销进行实验对比,为确保测试过程所得结果稳定,每组实验单独运行30次求取实验结果的均值进行对比测试。表2为本文算法与选取的3种对比算法的实验对比结果。
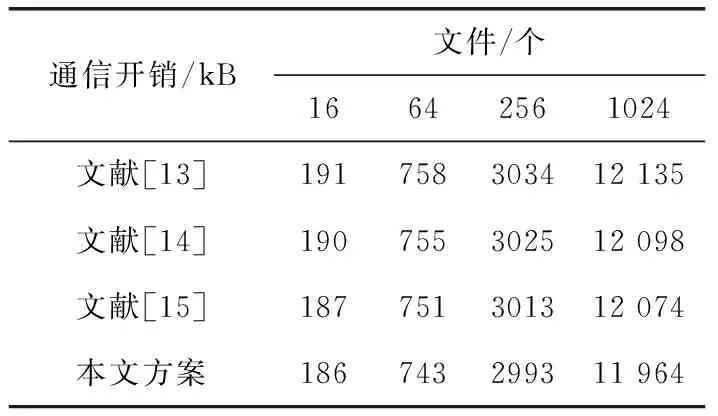
表2 通信开销测试数据对比
根据表2实验数据可知,在算法的通信开销指标上,本文所提的云存储数据融合算法相对于选取的文献[13-15]这3种云存储对比算法具有较为显著的性能优势。随着文件数量的增加,数据云存储过程的通信开销均逐渐增加,并且本文算法相对于选取的对比算法的通信开销优势逐渐增加,上述实验结果验证了所提算法在云存储数据通信开销指标上的性能优势。
首先,利用本文算法与最差设定实验情形进行对比实验,即失效文件多数是成对出现。图3为最差情形下,批量审计次数指标随失效文件个数变化对比情况,模拟测试过程中设置文件总个数是256个。

图3 批量审计次数实验对比(最差)
根据图3结果可知,在最不理想情况下,对于选取的几种对比实验算法中,本文算法的批量审计次数最少,这表明所提算法在给定失效文件情况下,所需要的失效文件审计指标最佳。对比算法中,文献[13]算法因为需要对失效文件交叉内容进行重复性质的查询操作,因此其在失效文件审计指标上要高于文献[14]算法,表明其针对失效数据的处理能力要弱于文献[14]算法。文献[15]算法设计了一种快速识别算法,但是在最差实验环境下,失效文件往往多数是成对出现的,这种实验环境下,无法有效发挥文献[15]算法快速识别过程的有效性,因此在实验结果上的表现就是文献[15]算法的批量审计指标虽然要优于文献[13,14]算法,但是与本文算法相比仍有较大的差距。
其次,为了对上述情况进行对比分析,选取随机情况再次进行实验模拟,对比算法仍然选取文献[13-15]这3种算法,实验对比结果如图4所示,模拟测试过程中设置文件总个数仍是256个。

图4 批量审计次数实验对比(随机)
根据图4结果可知,在随机情况下,对于选取的几种对比实验算法中的本文算法的批量审计次数仍然最少,这与最差情形下的实验结果一致,表明本文算法具有更广的适应性。同样,与最差情形相似,对比算法中文献[13]算法因为需要对失效文件交叉内容进行重复性质的查询操作,因此其在失效文件审计指标上要高于文献[14]算法。由于设定为随机实验情形,因此文献[15]算法设计的快速识别过程具有一定的效果,与本文算法实验结果具有相对的接近性。
对于选取的256个模拟测试过程的总文件个数,设定其中失效的文件总数是17个,这些失效文件仍然采取随机方式进行分布设置。对比算法仍然选取文献[13-15]这3种算法,实验指标选取查询时间,单位是ms,实验结果如图5所示。
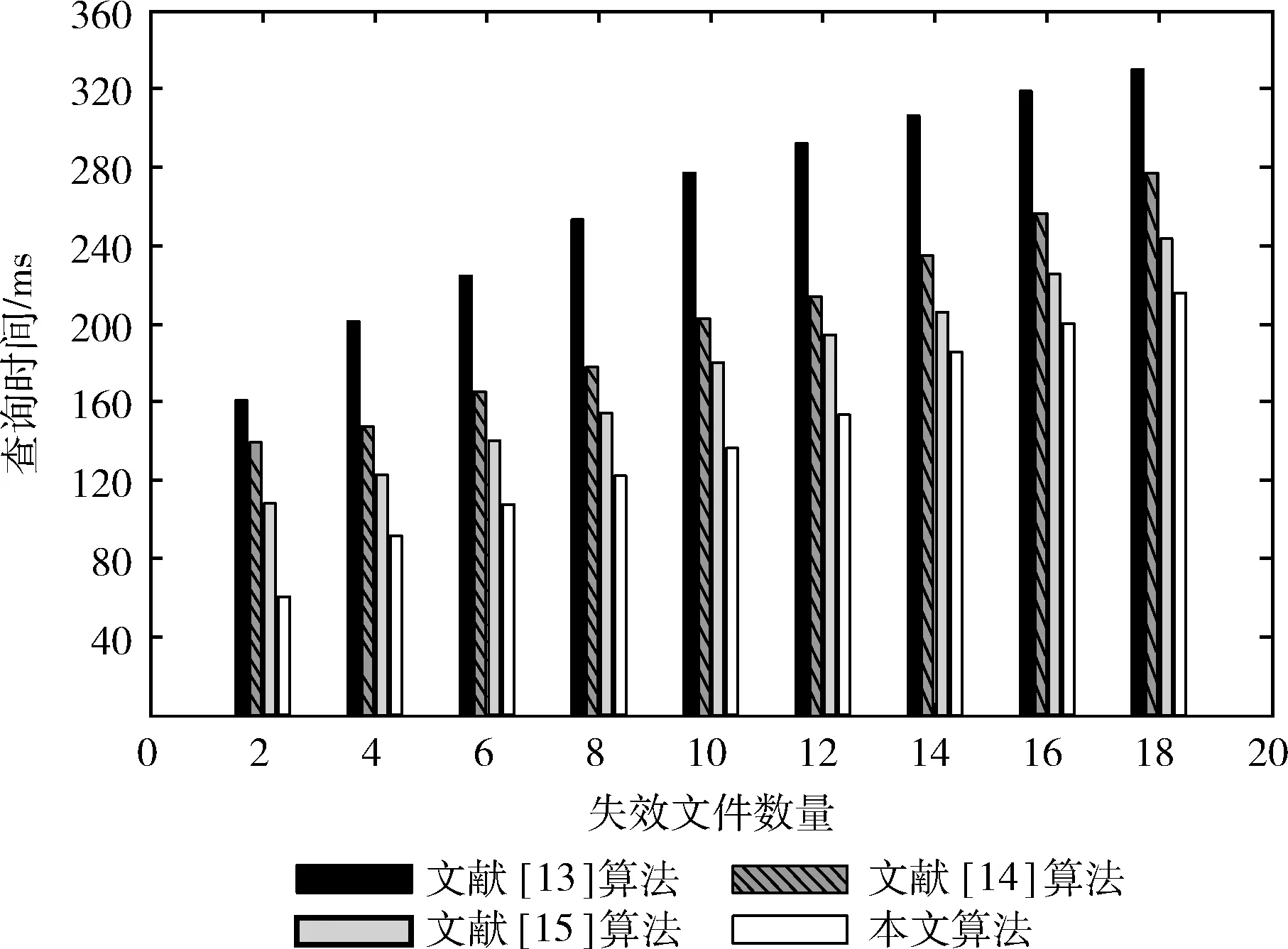
图5 查询时间对比
根据图5所示实验结果,文献[13]算法因为需要在查询过程中首先对测试数据的行列数据进行审计定位,因此其在查询时间上相对于选取的对比算法具有更高的查询时间。对于少量文件损坏情形,因为文献[15]算法选取的是一种幂指查询方式,因此其数据查询时间相对较快,但是在文件损坏数量增加后,算法的查询时间逐渐增加,并且查询时间的增加幅度要显著高于本文算法。文献[14]算法查询时间指标介于文献[13]和文献[15]两种算法之间。根据上述时间结果可知,本文算法在查询时间指标上也要优于选取的对比算法,体现了所提算法的性能优势。
4 结束语
本文提出的滤波器采用一种模糊技术来解决Bloom滤波器的空间需求问题。我们验证了所提出的方法可以在同一空间容纳更多的元素。与SBF相比,由于所提出的滤波器仅包含二元集合上的简单模糊运算,因此交叉和与之相关的运算的代价几乎可以忽略不计。压缩后的误报率与标准Bloom滤波器相同。由于使用了双哈希技术,两个哈希函数生成k个哈希函数,因此哈希运算的计算时间也大大减少。FFBF的查询复杂度取决于Bloom滤波器被划分的块的数量。从m大小的Bloom滤波器和相同大小的压缩表示中搜索元素保持不变。实验结果验证了所提算法有效性。下一步,①对双哈希模糊交叉Bloom滤波器进行进一步改进,提高算法计算效率;②考虑引入稀疏数据表示方式,对算法执行效率进一步改进提升;③考虑实际应用软件开发,验证真实环境算法性能。
