基于Spark的倾斜数据虚拟划分算法

李俊丽

(晋中学院 计算机科学与技术系，山西 晋中 030619)

0 引 言

随着大数据时代的到来，数据量以惊人的速度增长。大数据应用的出现给数据处理带来了巨大的挑战[1,2]，越来越多的高效并行计算平台，如MapReduce[3]和Spark[4-6]，被广泛采用来处理大数据。互信息是对两个随机变量之间共享的信息量的度量。互信息的计算量很大，特别对于处理大规模的类别数据。互信息可以广泛应用于数据挖掘[7,8]算法中。为了提高互信息计算的效率，Spark内存计算模型是最好的选择，但要面对Spark数据倾斜的性能优化问题。针对Spark中的数据倾斜问题，近年来提出了很多算法和模型。例如，文献[9]提出了Spark平台上基于特征分组的并行离群挖掘算法。SCID算法[10]设计了一种Pond-sampling算法来收集数据分布信息，并对总体数据分布进行估计。在数据划分过程中，SCID实现了Bin-packing算法对Map任务的输出进行桶状处理。此外，在分区过程中，还会进一步切割大型分区。SP-Partitioner算法[11]将到达的批次数据作为候选样本，在系统抽样的基础上选择样本，预测中间数据的特征。该方法根据预测结果生成参考表，指导下一批数据的均匀分布。文献[12]优化了笛卡尔(笛卡儿积)算子。由于计算笛卡尔积需要连接操作，因此可能会出现数据倾斜。文献[13]提出了SASM(Spark adaptive skew mitigation)，通过将大分区迁移到其它节点，同时平衡各任务之间的大小，来缓解数据倾斜问题。与这些现有的方法不同，DVP算法针对文献[9]中并行互信息计算中出现的数据倾斜问题进行研究和改进。DVP算法探索了数据虚拟划分，其中虚拟前缀附加在一个大分区中的所有键之前，然后是一个辅助散列。DVP中的虚拟分区确保消除了大分区。DVP算法是在Spark计算平台上设计并实现的一种数据虚拟划分的方案，主要针对数据倾斜情况下大规模类别数据的互信息并行计算，解决了数据分布不均匀导致的数据倾斜问题。

1 互信息计算

互信息是信息论中对两个随机变量关联程度的统计描述，可以表示为这两个随机变量概率的函数。

假设DS是一个包含n个对象的数据集，每个对象都由m个特征表示。我们使用H(yi,yj)和MI(yi;yj)分别表示集合DS上计算的特征yi和yj之间的熵和互信息。熵可以表示如下

(1)

其中，Pij(yi=vik∧yj=vjl)为特征yi和yj分别等于vik和vjl的概率。式(1)中di和dj为特征yi和yj的取值个数；vik和vjl可以在集合D(yi)和D(yj)中找到，其中D(yi)={vi1，…，>vidi}，D(yj)={vj1，…,>vjdj}。熵H(yi,>yj)是概率Pij和logPij的乘积的函数。

MI(yi;yj)作为特征yi和yj之间的互信息。我们将互信息MI(yi;yj)表示为

(2)

其中，概率Pij，特征yi和yj，值vik和vjl，域di和dj，集合D(yi)和D(yj)与式(1)中的相同，Pi和Pj分别为特征yi和yj等于vik和vjl的概率。

互信息可以广泛应用于数据挖掘算法中，DVP算法中的互信息是作为度量指标来量化类别数据特征之间的相似性。

2 数据倾斜

2.1 概 述

在Spark Shuffle阶段，Spark必须将相同的键从每个节点拉到节点上的任务中。这样的过程可能会给单个节点带来沉重的负载。此时，如果某个键对应的数据量特别大，就会出现倾斜。

图1描述了分区2总体上比分区1和分区3大。由于输入数据分布不均匀，使用系统的默认哈希分区可能导致子RDD中每个分区的大小存在较大差异，从而导致数据倾斜。当遇到数据倾斜问题时，整个Spark作业的执行时间由运行时间最长的任务控制，这使得Spark作业运行得相当慢。在最坏的情况下，由于最慢的任务处理了过多的数据，Spark作业可能耗尽内存。

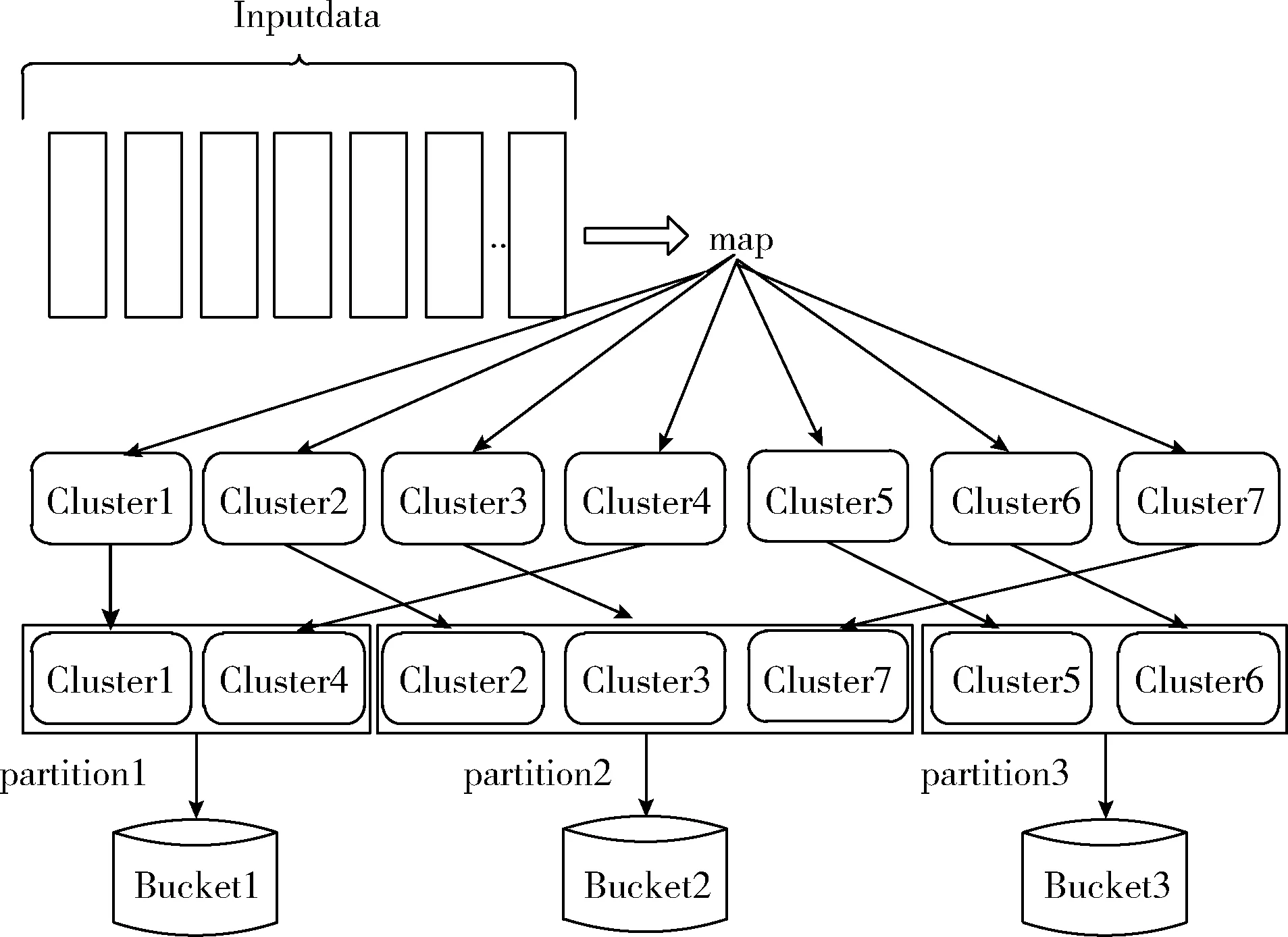
图1 Spark Shuffle数据分布

2.2 数据倾斜模型

接下来建立了一个数据倾斜模型来量化由Spark创建的分区之间的数据倾斜度引起的问题。

图1描述了Spark集群中默认的哈希分布机制，该机制执行以下3个步骤。首先，Map任务检索输入数据。然后，这些数据由Map任务处理，Map任务生成以键值对格式组织的中间结果。最后，使用键将中间结果分组到分区中。最后一步中的一个障碍是，由于数据倾斜，这些分区的大小不均匀。

假设根据键值聚合数据时有p个唯一的键，我们设K表示键，K={k1,>…,>kp}。我们把V表示为集合k中所有键的值

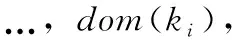
(3)

假设有p个分区，每个分区中的值共享一个键。值得注意的是，所有分区的大小可能不同。例如，第i和第j个分区的大小分别为li和lj。这两个分区的大小可能不同(即li≠lj)。

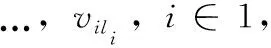
现在使用域dom(ki)的大小来度量键ki的第i个分区的大小，它的形式是|dom(ki)|。平均分区大小由|dom(K)|avg表示，|dom(K) |avg由平均域大小来衡量，具体如下表示

(4)

分区之间的数据倾斜度定义为分区大小的偏差(即，|dom(ki)|)。设(ki)为第i个分区或域dom(ki)的倾斜度。在形式上，域dom(ki)的倾斜度s(ki)如下表示

(5)

3 数据虚拟划分方法

3.1 并行互信息计算中的数据倾斜

聚合操作符是Spark Shuffle阶段的性能瓶颈。并行计算互信息的一个关键挑战在于countByKey或reduceByKey操作符(参见算法1第(4)行和第(12)行)，它引入了包含两个阶段的shuffle。在shuffle过程中，第一阶段执行shuffle write操作分区数据。具有相同键的已处理数据被写入相同的磁盘文件。

一旦countByKey或reduceByKey操作符执行，第二阶段中的每个任务都会执行shuffle read操作。执行此操作的任务提取属于前一阶段任务节点的键，然后对同一键执行全局聚合或连接操作。在这个场景中，键值被累积。如果数据分布不均匀，就会发生数据倾斜。

3.2 数据虚拟划分

数据虚拟划分是一种针对shuffle操作(例如，reduceByKey)可能引起数据倾斜而进行的虚拟分区机制。为了减少shuffle操作中的数据倾斜，DVP算法只在统计单个特征的取值时进行虚拟分区，因为特征对的取值不容易发生数据倾斜。图2描述了虚拟分区的过程。

图2 虚拟分区过程

在这里，首先为RDD中的每个键添加一个随机前缀，然后是reduceByKey聚合操作。通过向同一个键添加随机前缀并将其更改为几个不同的键，一个任务最初处理的数据被分散到多个任务中，以便进行本地聚合。这种虚拟分区的策略减少了单个任务处理的过量数据。删除每个键的前缀后，再次执行全局聚合操作以获得最终结果。

3.3 DVP算法描述

DVP算法主要由以下基本步骤完成：首先，使用关键字val定义一个可变长数组doubleCol用于存放特征对的计算结果。其次，使用map映射操作将RDD数据datapre转换为键值对的形式，即pair((x(m);x(n));1)。值得注意的是，((x(m);x(n))是特征对m和n的取值；1表示特征对的值出现一次，并且记录每一对特征对取值的整体出现情况。然后，使用关键字val定义另一个可变长数组singleCol用于存放单个特征的计算结果，由于在计算单特征值时容易出现数据倾斜，为了缓解数据倾斜问题，最后需要对单个特征的取值进行数据虚拟划分。

具体算法如下：

算法1：DVP算法

输入：数据集DS(nobjects ×mfeatures)，由数据集生成的名为 datapre的RDD

输出：两个变长数组

(1) val doubleCol = new Array [ArrayBuffer [Map [(String, String), Long] ] ](dimension) //关键字val定义了一个可变长度数组，即doubleCol

(2) for (m= 0;m≤dimension;m++)

(3) for (n= 0;n≤dimension;n++)

(4) doubleCol(m)(n)+ = datapre:map(x≥((x(m);x(n)); 1))>.countByKey()>.toMap //将RDD数据的datapre转换为pair ((x(m); >x(n));>1)使用映射转换，并计算特征对取值的整体出现情况

(5) end for

(6) end for

(7)val singleCol = ArrayBuffer[Map[String,Long]]() //关键字val定义了一个可变长度数组，即singleCol

(8) for (k= 0;k≤dimension;k++)

(9) singleCol+= datapre.map

(10) val random:Random = new Random()

(11) val prefix:Int = random.nextInt(10)

(12) prefix+-+x(k)，1)).reduceByKey(-+-).map (line ≥(line.-1.split("-")(1), line.-2)).reduceByKey (-+-).collectAsMap().toMap // 数据虚拟划分

(13) end for

4 实验结果及分析

4.1 实验环境

DVP算法在一个配备了24个节点的Spark集群中实现并验证，每个节点都有一个Intel处理器(即，E5-1620 v2系列3.7 GHz)，4芯16 GB RAM。主节点硬盘配置为500 GB；其它节点的磁盘容量是2 TB。集群中的所有数据节点都通过千兆以太网连接；使用SSH协议保证节点之间的通信。我们在Spark的standalone模式下实现了DVP算法。

在DVP实现中使用的编程语言是Scala，这是一种在Java虚拟机(JVM)上运行的函数式面向对象语言。Scala无缝集成了现有的Java程序。利用集成开发环境IntelliJ IDEA开发了DVP算法。

表1中列出了DVP算法中所用到的Spark集群的配置情况。

表1 Spark集群中的软件配置

4.2 人工数据集

DVP使用人工合成类别数据集来进行性能评估。为了评估DVP算法，构造了两种类型的合成数据集：均匀分布数据集和正态分布数据集。通过以下两个步骤生成数据集。首先，创建一个相对较小的类别属性数据集。接下来，不断复制第一步中创建的数据集，以扩大数据集的大小。合成数据集包含100个特征，这些数据集的大小分别为8 GB、16 GB、24 GB和32 GB。数据集见表2。

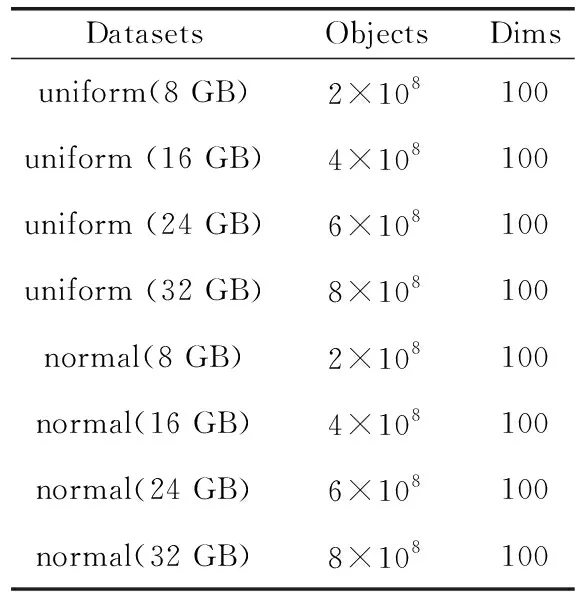
表2 人工合成数据集

4.3 比较算法DEFH

DEFH是使用最广泛的哈希算法，是Spark中的一种默认机制。当键值呈现均匀分布时，可以获得较好的性能。

4.4 实验分析

(1)不同数据大小下的执行时间：图3为DVP和DEFH算法处理不同数据大小的均匀分布数据和正态分布数据所使用的运行时间。分别将数据大小设置为8 GB、16 GB、24 GB和32 GB。计算节点的数量配置为24个。

图3 不同数据大小下均匀分布和正态 分布数据的执行时间

由图3(a)可以看出，在分布均匀的数据集中，由于虚拟分区的副作用，DVP算法的运行时间比DEFH稍长。然而，从图3(b)可以看出，对于正态分布的数据集，DVP算法优于DEFH。这是预期的结果，因为正态分布数据集包含了分布不均匀的数据，导致了数据倾斜，从而耗费了时间。而由虚拟分区支持的DVP算法可以很好地处理倾斜数据。

另外，从图3(a)和图3(b)还可以看出，增加数据量会导致所有算法的运行时间增加。直观地说，这是因为处理大规模数据需要更长的时间。

(2)不同计算节点下的执行时间：图4展示了DVP和DEFH算法在不同数量的计算节点上处理均匀分布数据和正态分布数据所使用的时间。节点的数量分别配置为4、8、16和24。数据大小设置为8 GB。图4(a)显示，由于虚拟分区的开销，我们的DVP算法在均匀分布数据中的运行时间要比DEFH的运行时间长。这一趋势与图3(a)所示一致。图4(b)显示，在不均匀分布的情况下，正态分布数据集中DVP算法的性能要明显优于DEFH。DVP在DEFH上的性能改进归功于数据虚拟划分，它有效地缓解了数据的倾斜。同样，这些结果和图3(b)所描述是一致的。

图4 不同数量节点下均匀分布和正态 分布数据的执行时间

另外，从图4(a)和图4(b)还可以看出，随着计算节点数量的不断增加，两个算法的运行时间都有所减少。这主要是因为集群计算能力的不断增加。

(3)数据倾斜度的影响：由于均匀分布数据集中不会发生数据倾斜，因此选择正态分布数据集进行实验。从处理时间的角度对数据倾斜度的影响进行了评价。

图5显示了不同数据倾斜度下DVP和DEFH算法的处理时间，倾斜度从1到3不等，增量为0.5。我们观察到，DVP算法的处理时间对数据倾斜度的敏感性小于DEFH。例如，当我们将倾斜度从1.5提高到3时，DVP和DEFH算法的处理时间分别增加了7.2%和28.4%。实验结果表明，DVP算法利用数据虚拟划分有效地缓解了数据倾斜带来的性能问题。因此，在不平衡数据集中，DVP算法优于DEFH。在较高的数据倾斜度下，DVP算法对数据倾斜的改善更为显著。

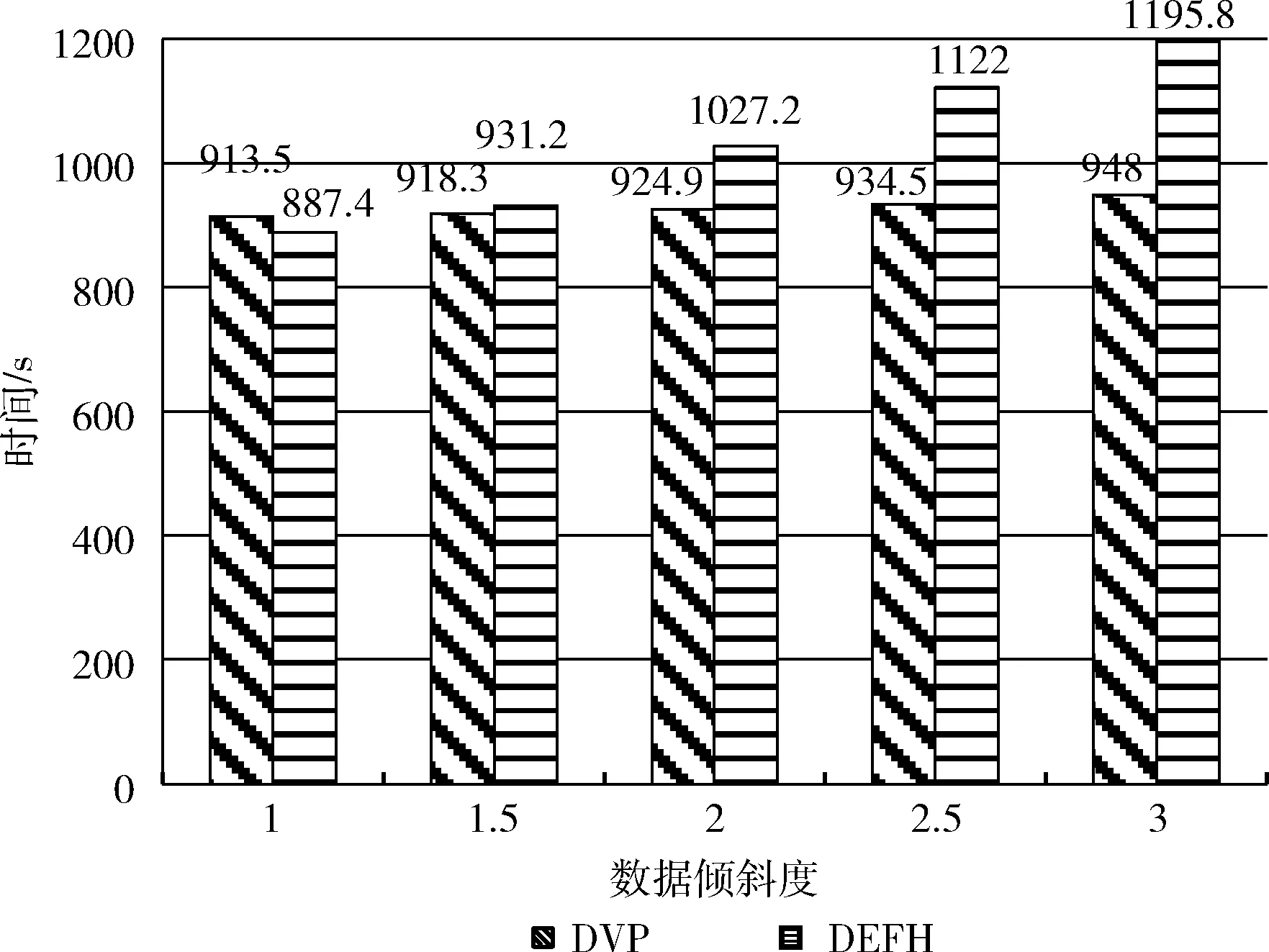
图5 数据倾斜度对DVP和DEFH处理时间的影响

(4)Shuffling-Cost分析：通过改变计算节点的数量来比较DVP和DEFH算法的Shuffling-Cost成本。以节点的shuffle-write-size作为对算法的Shuffling-Cost进行监控。以正态分布数据集(8 G)为例，图6是两个算法Shuffling-Cost对比。

图6 不同数量计算节点上的DVP和DEFH的 Shuffling-Cost

显而易见，所有测试用例中DVP算法的shuffle-write-size都明显小于DEFH。更重要的是，随着计算节点数量的不断增加，两种解决方案之间的shuffle-write-size差距也在扩大。DEFH依赖于Spark的默认哈希分区，导致任务频繁地跨多个节点访问数据。例如，当节点数量从4个更改为24个时，DEFH算法的shuffle-write-size从667.0 MB上升到1590.0 MB。与DEFH算法不同的是，DVP算法利用了数据虚拟划分技术来减少Spark环境中的数据传输量。因此，DVP算法的shuffle-write-size仅仅从260.0 MB跳到628.0 MB。就shuffling-cost而言，这比DEFH的情况要好得多。

(5)可扩展性分析：在这组实验中，通过增加计算节点的数量(分别设置为4、8、16和24)和调节数据集大小(配置分别为8 GB、16 GB、24 GB和32 GB)，对DVP算法进行可扩展性分析，评估DVP算法在集群系统中处理大规模数据的能力。

图7(a)显示了Spark集群中节点数量对并行互信息计算时间的影响。由图7(a)可以看出，随着计算节点数量的增加，DVP算法的执行时间明显减少。大数据集(如32 GB)的下降趋势非常明显。当数据集很小(例如4 GB)时，集群扩展性能提高很微弱。结果表明，DVP是一种对大数据集具有高扩展性的并行计算方法。

图7 DVP的可扩展性分析

图7(b)展示了计算节点数量对系统加速的影响。从图7(b)可以看出，对于大多数数据集来说，DVP的加速率接近线性。例如，在32 GB的情况下，DVP的加速性能几乎与线性性能相当。结果表明，我们的并行计算算法能够保持大规模高维类别数据集的计算性能。

上述DVP的高可扩展性主要归功于以下几个因素。首先，并行互信息计算的时间在很大程度上取决于任意两个特征之间的互信息计算，这种互信息计算时间与分配给节点的数据对象数量成正比。其次，所有计算节点都独立地并行计算。最后，由于数据虚拟划分，DVP在所有节点之间保持了良好的负载平衡性能。

5 结束语

本文基于Spark平台开发了DVP算法，在大规模类别数据的背景下并行计算互信息。DVP的核心是数据虚拟分区方案。更具体地说，虚拟分区技术缓解了shuffle过程中出现的数据倾斜问题。最后在一个24节点驱动的Spark集群上采用人工合成类别数据集验证了DVP算法。

大量的实验结果表明，该算法在效率和负载均衡等方面优于Spark集群默认的DEFH算法。此外, 在Spark处理大型类别数据集时，DVP能够很好地减轻数据倾斜，从而优化网络性能。

在未来的工作中，将重点从内存资源的角度优化shuffle性能。当数据分布变得不均匀时，分配给分区的数据量就不平衡。因此，任务所需的内存空间本质上是不同的。如果给每个任务分配固定比例的内存空间，任务中频繁的内存溢出将是不可避免的。这样的内存资源问题会对Spark的整体性能产生负面影响。打算研究一种分配内存资源的方法，以进一步优化所有任务之间的shuffle进程。该技术有望从内存计算的角度提高Spark应用程序的性能。