不同地质条件下振动信号特征识别研究
2021-08-23黄安贻唐异平
黄安贻,唐异平
(武汉理工大学 机电工程学院,湖北 武汉 430070)
地下油气输送管道、通信电缆等设备不易监管,偷盗损害现象时有发生。现有的报警方法多采用红外、图像、激光和光纤等传感器[1-5],这些方案具有铺设成本高,覆盖范围小等缺点。因此,地下空间的防盗报警多采用振动信号识别的方法。韩卫洁[6]从时域、频域和时频域方面对振动源目标的振动信号进行分析,实现了振动信号的识别。陈亚亚[7]对小波包去噪后的信号进行过零分析并提取去噪后信号的各项时域和频域参数指标;同时提取各IMF(intrinsic mode functions)分量的能量指标,将这些特征参数进行组合构造特征向量,利用支持向量机实现了对振动信号的准确识别。常用的识别振动信号的方法还有如傅里叶变换、短时傅里叶变换、HHT(Hilbert-Huang Transform)等[8-9]。但在实际应用过程中,管线跨越地理范围广,经常需要穿越不同种类的地质,而现有研究多针对单一地质,并没有考虑到多种地质的情况。针对这种情况,笔者展开了关于不同地质环境下的振动信号特征识别方法的研究,如泥地、沙地、公路等。对不同地质不同行为的振动信号采集分析,通过小波阈值去噪后使用EMD(empirical mode decomposition)并利用相关性分析得到特征波形。再利用能量过零算法计算特征波形的能量及过零率,使用Hilbert变换建立波形边际能量谱,通过多次实验统计并最终建立专家数据库,并提出一种二次判断方法去维护和建立统一的专家数据库,实现自适应功能,实现振动信号的有效识别。
1 振动信号识别系统
地面目标运动时会产生相应的地面振动信号,振动信号特性主要取决于地面地质条件、目标的运动行为和目标的距离,频率一般较低[10]。地表目标活动敲击地面形成振源,其产生的振动波以压缩波、剪切波、瑞雷波、乐夫波的形式在地球介质中传播。按照介质运动的特点及振动波的传播规律划分,可将振动波分为体波与面波,其中体波又包含纵波(P波)和横波(S波)。面波是体波在一定的条件下形成相长干涉并叠加产生出的频率较低、能量较强的次生波,主要沿着介质的分界面传播,面波又包含瑞雷波和乐夫波。上述各类波在地球介质中的传播形式如图1所示[11]。
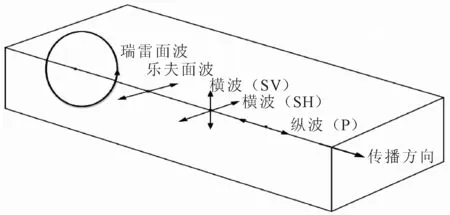
图1 弹性波传播示意图
瑞雷波在振动信号中能量约占振动总能量的70%且传播速度最低,能量的衰减也比体波弱,因而容易检波且具有较高的分辨率[12]。故检测地面运动目标时,瑞雷波是振动传感器检测的主要波形。由振动波波谱知[12],面波一般在低频处有极大值,主要频率在10~30 Hz之间;工业交流电干扰频率十分集中,主频是50 Hz;反射波主频在30~60 Hz内;风吹草动造成的微振频谱很宽,在60 Hz以上;声波频谱范围一般在100 Hz以上;车辆、走路等人为活动造成的振动信号频率主要集中在200 Hz以下,并且信号的主要能量集中在25~150 Hz的低频段,特征峰值频率较低。
根据检测波形的特点,使用的测量系统如图2所示。由安装针(硬质地面不选用),加速度传感器ADXL103/203,差分转换芯片AD8138,SDY2400数据采集仪及笔记本电脑构成。最后利用SDY2400数据采集仪采集被测信号,该采集仪接口为USB接口,A/D分辨率为12/16位,转换频率为100/200/300 kHz,采集通道数为16通道。数据采集仪配套软件为Vib’SYS,集成了振动信号采集、处理和分析程序。

图2 振动信号测量系统
2 振动信号特征识别方法
2.1 小波阈值去噪
根据地面振动所造成的瑞雷波的特点,通过硬件滤波的方式去除大部分噪声。但仍有部分低频噪声存在,这些噪音很难通过传统滤波器去除。考虑到所采集信号为非线性非平稳振动信号,因此采用小波阈值去噪技术能更好地提高信号的信噪比和处理速率。
原始一维信号模型A(i)为:
A(i)=f(i)+σ·e(i),i=0,1,…,n-1
(1)
式中:f(i)为真实信号;e(i)为噪声信号;σ为噪声标准差;A(i)为原始信号。
一般来说小波阈值去噪包括小波分解、去噪阈值量化和信号重构三个部分。
定义在Hilbert空间中,将小波函数族ψa,b作为积分核与有限能量函数f(t)做内积的变换称为小波变换,如式(2)所示。
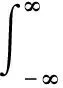
(2)
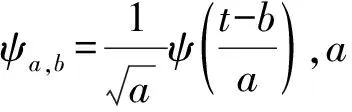
(3)
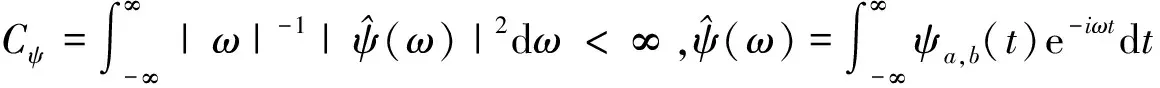
(4)
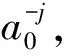
(5)
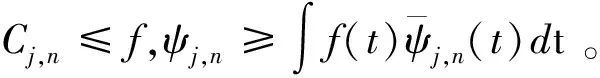
通过多次实验尝试选择SYM4小波基,小波分解后使用软阈值方法及stein无偏似然估计阈值(rigrsure)算法进行软阈值量化。使用软阈值的原因是防止硬阈值造成断点在信号还原时造成激荡从而影响信号的还原。使用软阈值函数将小于阈值的小波系数设定为0,如式(6)所示
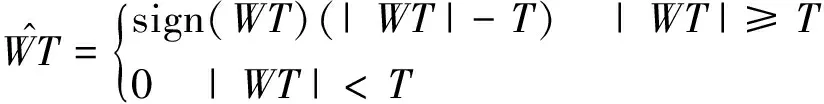
(6)
之后再将小波分量进行还原,得到滤波后的信号。
2.2 能量-过零及HHT特征提取
得到还原信号后便可以将还原信号进行HHT处理,获得信号的瞬时频率。HHT处理方法总共分为两个阶段,首先通过经验模式分解(EMD),将原始信号分解为若干模态函数(IMF)分量。经过分解后得到若干个IMF和一个残余趋势量,如式(7)所示。
(7)
IMF分量反映了原始振动信号在不同频段内组成成分,式中c1(t)、c2(t)、…、cn(t)的频率分布是由大到小排列的,rn(t)是残余的趋势项,EMD十分适合非平稳信号分析。
完成EMD后,将分解后的振动信号所得到的IMF分量分别计算与分解前信号的相关系数R,取相关系数前4高的IMF分量进行信号重构,得到特征信号。对特征信号C(t)采用Hilbert变换,进而得到特征信号的瞬时频率,将瞬时频谱整合即可得到Hilbert谱。
(8)
解析信号Z(t)=C(t)+iH[C(t)]=A(t)·eiφ(t)
式中:A(t)和φ(t)分别代表特征信号的瞬时振幅和瞬时相位。
(9)
(10)
由式(10)求导可获得特征信号的瞬时频率ω(t)如式(11)所示。
(11)
通过式(11)则有:
(12)
得到Hilbert谱如式(12),通过对Hilbert谱在时域内进行积分处理后即可得到Hilbert边际谱,如式(13)所示。

(13)
将得到的Hilbert边际谱进行随频率的平方和积分计算,得到Hilbert边际能量谱,定义能量随频率的分布状况如式(14)所示。
(14)
通过能量过零算法计算特征信号的能量M及过零率ZCR,如式(15)~式(16)所示。
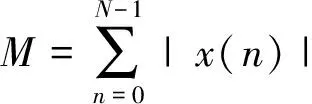
(15)
(16)
将Hilbert边际能量谱、能量M及过零率ZCR统一记录下来作为特征波形的特征数据。
3 基于能量过零联合HHT的特征数据库建立与自适应更新
通过对大量无影响标准信号的特征分析,分别计算出不同地质、不同行为的特征波形的能量M、过零率ZCR及Hilbert边际能量谱,利用这些特征建立两步辨识方法。
首先对能量及过零率进行统计分析,排除3σ原则之外的粗大误差。之后将同地质、同行为的特征信号的能量及过零率显示在二维空间上,计算其覆盖范围,作为初步识别的依据。接着将这些数据对应的Hilbert边际能量谱求解平均值,及与平均值差值数据的最大方差,作为第二步辨识依据。对所有地质及行为均按上述方法建立两部识别依据,建立统一专家数据库。单个类型数据库建立流程如图3所示。

图3 单个类型数据库建立流程
获得一段待识别信号后先进行小波阈值去噪,然后进行HHT变换得到Hilbert边际能量谱,再将得到的特征信号计算能量及过零率。这样就得到了这段信号的特征参数。首先将计算能量及过零率是否唯一匹配,如果唯一匹配则直接识别成功,如果不是唯一匹配,则求解Hilbert边际能量谱与已匹配种类的Hilbert边际能量谱差值的方差,方差最小且小于数据库内的最大方差则为匹配成功,否则为匹配失败。如果能量过零完全不匹配但Hilbert边际能量谱匹配成功,则可能由于各地地质状况安装方式又有细微不同,可能有虽为同类地质但振动特性仍有略微不同,因此进行数据库自适应性扩展,如果能量过零与识别区域的最近距离对应的能量与过零率在阈值内,则将该点加入专家数据库中,如果Hilbert边际能量谱匹配失败,则识别失败。信号识别和数据库更新流程如图4所示。这样便实现了特征数据库的建立和自适应更新。
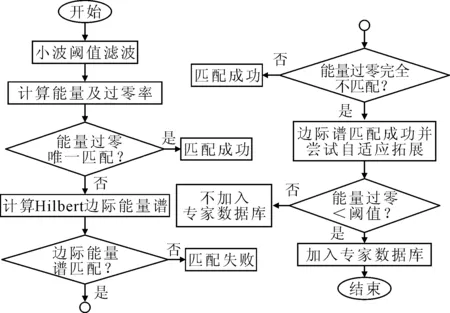
图4 信号识别和数据库自适应流程
4 振动信号识别实验验证
将实验装置安置在草皮泥地地面、沙地地面、砂土地面、砖地地面和柏油公路地面地质条件下,分别进行40次人员行走、敲击和挖掘动作(部分硬质地面无法挖掘),并记录信号,同时再记录不同地质下人员行走、挖掘、敲击等信号共240组用以验证。实验过程中走路信号为55 kg成年男子在检测范围内正常走路产生的信号,敲击信号为5 kg橡胶锤在检测范围内无加力情况下敲击地面产生的信号,挖掘信号为使用铁锹非固定姿势挖掘地面产生的信号,所有信号并没有固定信号产生的具体位置。将信号经过处理建立统一数据库,得到能量过零率分布图如图5所示,Hilbert边际能量谱如图6所示。可以看到通过能量过零区域判断及边际能量谱判断能够有效地区别不同地质不同行为所产生的振动信号。

图5 能量过零分布图
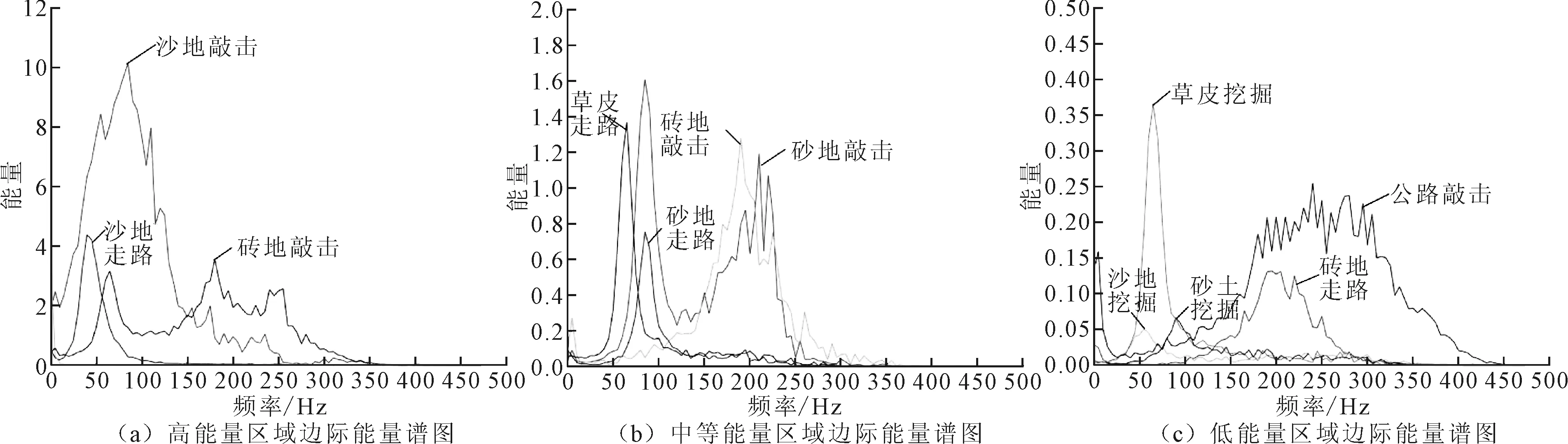
图6 边际能量谱图
使用不同地质条件的振动信号进行测试,每个类型20组实验信号,验证识别方法的有效性,识别率计算公式如式(17)所示。
(17)
式中:Q为识别成功率;P为每组识别成功的信号组数。
验证信号识别率如表1所示。结果显示本方法有较好的识别精度。之后又重新测量了15次另一位置公路地面的敲击信号,能量阈值设定为1.5,过零阈值设定为0.01。验证数据库的自适应能力,得到能量过零区域分布图变化如图7所示。圆点为新测量的敲击信号,虚线为自适应之前的判断范围,实线为自适应之后的判断范围。从实验结果可以看到边际能量谱作为振动信号的识别特征更精确和稳定,但数据量大,计算较为麻烦,使用能量过零算法虽然在判断区域上有一定重叠但作为初步判据是快速有效的。
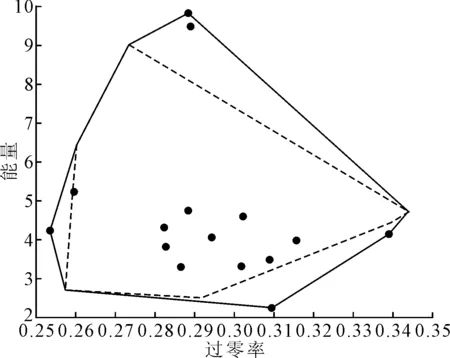
图7 公路敲击数据库自适应过程
5 结论
实验表明了不同地质条件下振动波形的特征有所不同,一种地质的特征不能与其他地质的特征相匹配。针对该问题笔者利用能量过零联合HHT算法有效地识别了不同地质不同动作的特征,并通过建立统一专家数据库成功识别了不同地质不同动作所产生的振动信号。使用阈值判断及边际能量谱匹配实现了数据库的自适应性拓展,并通过实验验证了该方法的有效性。但对于未记录在库的地质及动作无法进行识别,后续会利用机器学习等大数据分析方法更精确地获得特征来实现数据库更强的适应性。
