基于FPGA的特征降维算法实现
2021-08-23黄德湖郑晓亮
周 晓,黄德湖,郑晓亮
(武汉理工大学 机电工程学院,湖北 武汉 430070)
图像特征提取是实现目标识别算法的一个重要步骤,许多优秀的目标识别算法[1-4]依靠提取有效的图像特征获得了极高的识别率。为了获取出色的识别精度,所提取的特征信息必须足够丰富,这使得算法需要消耗大量的资源进行运算。巨大的计算量在带来优秀的性能表现的同时,也带来了计算资源和时间效率的问题。FPGA(field programmable gatearray)因为其高并行和高吞吐率的特点,使得许多图像处理算法以其作为实现平台进行优化加速[5-6]。
在特征提取算法中,图像的高维特征包含的信息并不完全是研究人员所需要的,在每维度的数据间还存在冗余特征。这些冗余信息不仅妨碍对有用的信息进行筛选,还使数据量变得十分庞大,占用了更多的存储空间,浪费了大量的系统资源。PCA(prinicpal component analysis)技术可使高维数据变为维数较低的数据,并包含了原始数据中的大部分信息,在图像特征提取的领域得到了广泛应用。
LARK(local adaptive regression kernel)算子是韩国学者Hae Jong Seo提出的一种图像特征提取方法[4]。相比许多基于直方图统计的特征描述算子,LARK算子提取的特征信息更为丰富[7]。然而,将所有的特征信息一起用于分析,又会造成信息冗余度过高的问题。因此,在提取出原始LARK特征后,需要进行PCA降维计算,以避免后续分析的计算资源过度消耗。PCA算法中的协方差运算、特征向量分解和线性空间投影等计算需要消耗大量的运算资源,并且需要消耗大量的运算时间。笔者利用PCA算法原理,对图像LARK特征进行降维,并提出了相应的硬件架构,极大地提高了算法的运行效率。
1 算法原理
1.1 LARK特征简介
LARK是基于经典核回归的一种特征描述方法,算法的核心思想是通过梯度图像的自相似性来获取稳定的特征[8-9]。在LARK算子的理论中,图像是一个三维曲面,通过像素点的空间曲线距离来衡量像素的相似性。其特征提取公式为:
(1)
式中:l∈[1,2,…,P],P为选定窗口内像素的总数;Cl是基于像素梯度建立的协方差矩阵;Δxl是以x点坐标为中心的像素点坐标矩阵。x为像素点空间坐标,s为像素点的距离。在图像的每一个像素点处,协方差矩阵Cl都是不同的。因此,LARK算子并不是单一的利用高斯回归核进行计算,而是根据每一像素点处的梯度大小进行回归核形状的调整。在这样的特性下,LARK描述的特征信息是十分丰富的。
LARK算子描述了在选定的窗口内,窗口中心像素与其他像素的相似性。因此,窗口尺寸大小对计算量的影响十分巨大。在本文的研究中,选取了尺寸为5×5的窗口,对应的原始LARK特征为25维。
1.2 PCA算法
PCA算法是一种用于降低数据集维度的统计技术。它的主要思想是,在尽可能减少信息损失的情况下,找到一种降低数据维度的方法。直观地说,PCA技术通过查找数据中方差最大的方向,根据数据的重要性对数据进行排序。PCA的使用可以看作是一种线性变换,它为原始数据集选择一个新的坐标系,其中数据集中方差最大的方向被选择为第一主轴。PCA计算公式如下:
K=VΛV-1
(2)
Y=XVT
(3)
式中:K为数据X的协方差矩阵;V为正交矩阵,并且矩阵中的列向量为K的特征向量。数据在矩阵V上的投影结果为数据的主成分。新的数据集Y包含了了原始数据集X的主要信息,其信息维度由矩阵V的维度决定。
通常情况下,用特征向量对应的特征值大小代表数据在此方向上的能量,当矩阵V中的特征向量对应的能量值超过设定值时,就可将矩阵V当做数据的投影矩阵。
PCA算法的主要目的是寻找一种线性变换关系,使得原先具有p维度的数据集X,经过变换后可以表示为具有更低维度l的数据集Y。算法的整体架构如图1所示。
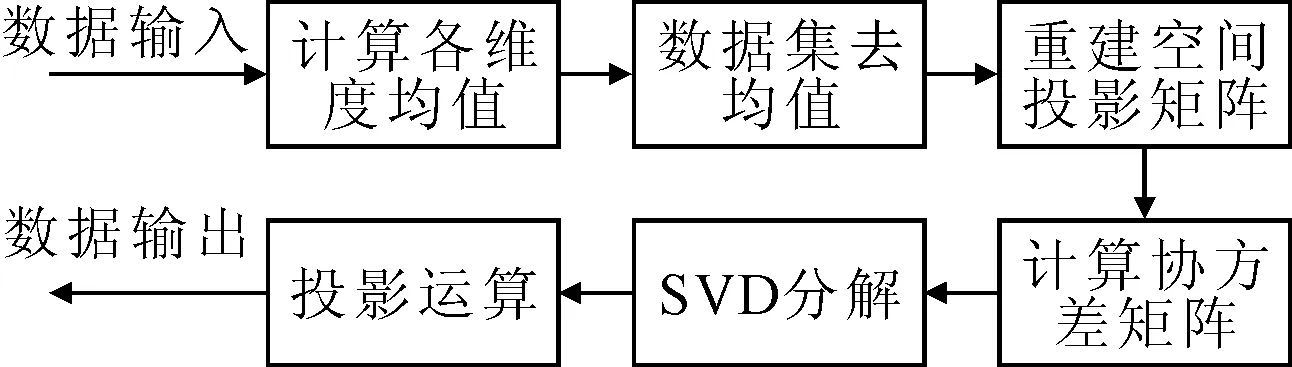
图1 算法整体架构
PCA算法的计算步骤如下:
(1)组织数据集。假设数据集是一系列向量组合x1,x2,…,xn,其中xi是一个具有p个元素的向量,可将向量组表示为一个维度为n×p的矩阵。
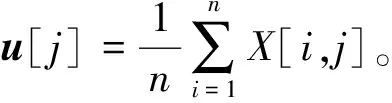
(3)计算数据集的去均值特征。将数据集的每一列都减去当列的平均值,将计算结果储存在矩阵X=X-huT,其中h为n维列向量,并且每个元素值为1。
(4)计算协方差矩阵。计算数据集的均方差矩阵C=XTX,其中XT为矩阵X的转置矩阵。
(5)计算协方差矩阵的特征值与特征向量。将矩阵C对角化:V-1CV=D,其中D为一个对角矩阵,矩阵对角线上的值为矩阵C的特征值。矩阵V由矩阵C的p个特征向量构成,特征值和特征向量一一对应。
(6)重组特征值和特征向量。将特征值降序排列,并将特征值对应的特征向量也进行相同的调整,确保特征值与特征向量的对应关系。
(7)选择特征向量作为新的基向量。选取特征值最大的L个特征向量作为新的数据集Y的基向量,并将这些向量组成投影矩阵W。
(8)利用投影矩阵对数据进行映射。投影矩阵的每个向量为协方差矩阵的特征向量,以这些向量作为新的数据集的基向量,可以得到原始数据中具有最大代表性的数据。新的数据集Y=XWT,数据的维度为n×L。
2 算法的FPGA架构
算法的硬件整体架构如图2所示。系统中的数据输入预先存在DDR3芯片中,通过VDMA将数据传送到FPGA内部进行处理。系统采用Xilinx公司ZYNQ系列的FPGA芯片作为核心处理器件,该芯片内嵌了一个双核的ARM处理器,在整个系统中主要起到配置和调试作用。硬件逻辑处理模块主要负责PCA算法的降维运算,并将最终结果通过数据总线与ARM端进行交互。

图2 硬件整体架构
系统架构主要是基于ARM处理器和FPGA硬件逻辑实现的。值得注意的是,为了提高系统的运算时间效率,内嵌的ARM处理器不参与数据降维过程的运算。系统主要计算均由FPGA实现,在运算过程中使用流水线运算和并行运算等方法,极大地提高了系统的时间效率。
系统中的FPGA数据流图如图3所示。上位机将原始数据通过调试接口置入DDR3内存,进行定点化处理后再将数据流导入降维计算硬件模块进行处理。最后,计算结果通过VDMA搬运到DDR内存,再由上位机读取计算结果进行分析。整个系统中,原始数据格式为32位浮点数据,为了发挥FPGA的运算优势,文中将数据转换为32位定点数。

图3 系统数据流图
硬件处理模块如图4所示,主要包括定点数转换模块、协方差矩阵求解模块、SVD分解模块、RAM模块和重映射模块,对于定点数运算,FPGA在计算周期和运算资源的消耗上能显现出其突出的优势。定点数转换模块负责将VDMA传输过来的数据进行定点化处理,以节省内存资源及其后续运算资源的占用。定点数据再依次经过协方差运算、SVD分解和重映射运算得到计算结果。在协方差运算、SVD分解和重映射运算时,需要对数据进行缓存。因此用RAM资源作为共享内存,作为各个模块的输出缓存。

图4 硬件处理模块
协方差矩阵的计算过程如图5所示。首先,输入数据在存入RAM的同时进行累加运算,在所有数据输入完成后,进行除法运算得到数据的平均值。接着从RAM中读出缓存的输入数据,计算去均值结果,并将结果存入RAM覆盖原先的输入数据。最后,将RAM中缓存的矩阵进行乘法计算得到协方差矩阵并将其输出。至此,系统的RAM模块中保留了数据的去均值特征。

图5 协方差矩阵计算模块
图6展示了SVD模块对协方差矩阵进行SVD分解的过程。在SVD模块中,运用Jacobi算法对矩阵进行迭代运算[10]。模块主要包括:输入选择器、输入端口RAM、向量点乘模块、CORDIC模块、旋转计算模块和范数计算模块。协方差矩阵数据通过输入选择器缓存到双端口RAM中,作为迭代运算的起始数据。在数据输入完成后,从RAM中读取向量列进行点乘运算,再通过CORDIC模块计算得出向量旋转角度,根据角度进行旋转运算。旋转运算后,两个向量更新为互相垂直的向量,再将其通过输入选择器写入到RAM中代替原来的向量列。在进行若干轮迭代运算后,可以在模块中的双端口RAM中得到协方差矩阵的特征值和特征向量。
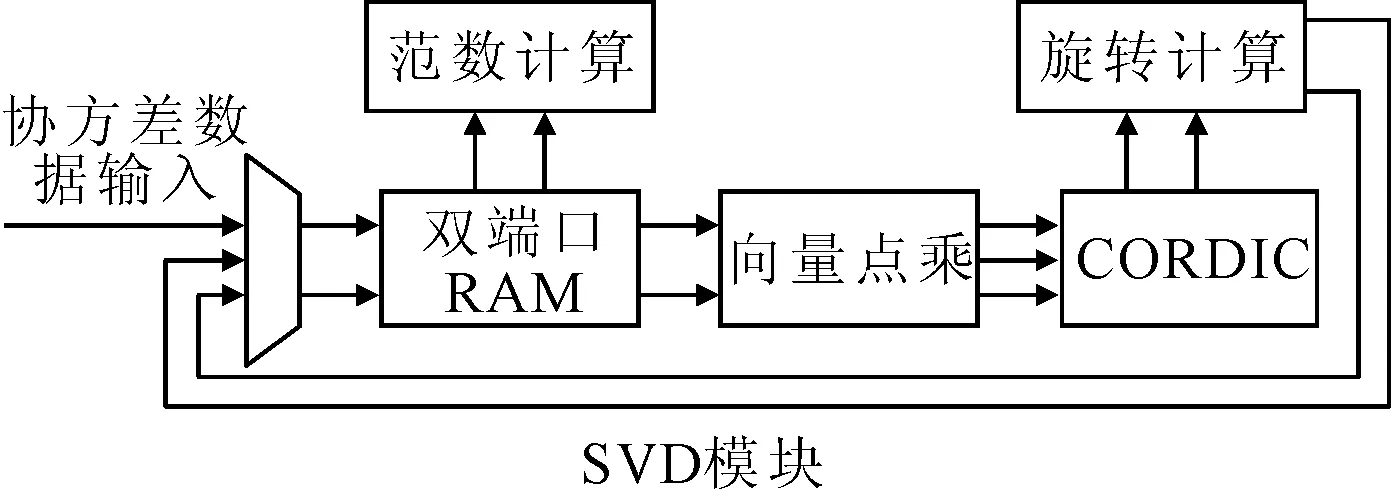
图6 SVD模块
在完成协方差矩阵的特征值分解后,得到了一组特征向量可以作为降维数据的向量空间。将数据的去均值特征在新的向量上进行投影运算即可得到数据的主成分。重映射的计算架构如图7所示。重映射模块中主要是数据的乘加法运算,因此其硬件结构主要由乘法器和加法器构成。对于输入的两个向量A=[a0,a1,…,an]和B=[b0,b1,…,bn],输入数据经过乘法器计算后得到第一层的结果为[a0×b0,a1×b1,…,an×bn]。结构的第二层由相邻的两个结果加法运算得到,在第三层进行第二层结果的加法运算,直到所有数据全部累加完成。为了利用FPGA的优势,需要对这个过程进行流水线优化,在每一层的计算结果完成后用寄存器进行缓存,可以是后续的计算结果流水输出。

图7 重映射模块
3 实验结果
设计选用了Xilinx公司ZYNQ系列的FPGA芯片作为算法的实现平台。整个算法的设计过程均由Verilog语言实现,芯片的内置ARM处理器在整个算法过程中负责调试配置等功能。算法运算过程中对FPGA的片上RAM资源有较大需求,因此设计平台选取了Xilinx公司的TySOM-2-7Z045/7Z100开发板,利用的硬件资源主要包括XC7Z100FPGA芯片和DDR内存。
系统输入为一个320×320分辨率图像的25维LARK特征,如图8所示。图像的LARK特征虽然包含了丰富的信息,但是有些特征图的差别很小。如果把所有的维度特征都作为图像的特征描述,在LARK特征的后续应用中将造成信息冗余,计算量极度增大等问题。利用前述架构对其进行降维运算,可以极大地提高算法的时间效率。

图8 输入图像的LARK特征
图9为图像特征进行降维后的数据信息保留度。在本文的设计中,降维计算后保留了前6维特征数据。进行PCA算法后,前6个维度的数据包含了原始数据90%的信息,同时减少了76%的数据量。算法开始前,需要将图像特征预存在DDR中,通过VDMA将DDR数据搬运到FPGA硬件实现模块处理。最后,硬件输出结果通过VDMA搬运到DDR中,由芯片内置ARM处理器和调试接口与上位机进行交互,硬件的输出结果如图10所示。

图9 维度序数与信息保留度关系
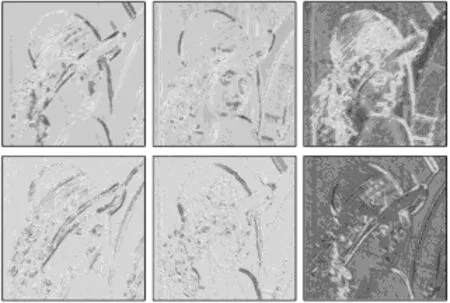
图10 硬件输出
表1为架构主要模块的硬件资源利用情况。由表1可知在协方差矩阵模块和重映射模块中,为了提高计算的时间效率,进行了大量的并行运算和流水运算,因此消耗的硬件资源很大。其中协方差模块中的RAM资源存储了输入的特征数据,被整个算法实现过程共享。

表1 硬件资源利用情况
表2为在不同平台下算法的运行时间。测试平台为搭载了I5-6300HQ处理器的PC,其主频为2.2 GHz,拥有16 GB的内存。在PC上,测得算法的运行时间为108.28 ms。在同样的输入数据下,文中提出的硬件架构只需要8.67 ms的运行时间,相对于PC处理速度大幅提升。

表2 算法运行时间
4 结论
笔者针对图像LARK特征存在的信息冗余特点,利用PCA算法原理,提出了基于FPGA的LARK特征降维算法实现。提出的架构主要包括:协方差矩阵计算模块、SVD分解模块以及重映射模块。对图像的LARK特征进行降维计算,提取出显著特征。通过实验表明,所设计的硬件架构比PC的时间效率大幅提高,可应用在实时性要求较高的场合。
