基于自适应模型预测算法的光伏并网逆变器无功电压控制策略研究
2021-08-23李德鑫王佳蕊张家郡庄冠群孙振奥
李德鑫,王佳蕊,张家郡,庄冠群,孙振奥
(1.国网吉林省电力有限公司 电力科学研究院,吉林 长春 130000;2.东北大学 信息科学与工程学院,辽宁沈阳 110819)
0 引言
分布式光伏接入电网后,改变了原电网的潮流分布,导致并网点(PCC)电压升高,随着渗透率提高而更加严重[1]。德国电网规定,分布式电源并网点电压不得超过额定电压的3%。我国相关标准也对并网点电压偏差作了规定[2]。
随着分布式电源的发展,并网点的无功电压控制逐渐引起学者关注。文献[3],[4]描述了多种电压控制方法,指出无功电压控制是目前最经济有效的电压控制方法。文献[5]~[7]介绍了无功电压控制的原理和可行性。文献[8]对德国电网规范推荐的3种无功电压控制方法进行了比较研究,指出各自的优缺点和适用场合。文献[9],[10]提出了无功注入控制策略,实现电网故障期间电压恢复,但未涉及线路阻抗特性和功率注入对公共耦合点电压恢复效果的分析。文献[11]通过无功功率来调节风电场并网点电压或提高电压可靠性的算法,该算法对光伏电站中的无功电压控制有很大的参考意义。目前的控制方法仍然不够智能,在一些特殊情况下会产生电压越限或收敛过慢的情况。文献[12]~[14]介绍了模型预测算法在风电场中的应用,通过无功输出控制风电场并网点电压,或提高电压稳定性。文献[15]将模型预测算法应用到分布式电源的有功无功调度中。文献[16]对模型预测算法的采样时间进行研究,指出采样时间过短会导致CPU的运算量太大;采样时间过长,不利于跟踪模型的变化,所以采样时间的选择要根据实际模型可能存在的变数速率选取。文献[17],[18]研究了模型预测算法在电压源型逆变器中的应用,结果表明,模型预测算法比传统PI控制有更好的动态响应。文献[19],[20]研究指出,在不影响控制效果的前提下,模型预测算法可以降低逆变器的开关频率,进而减小开关损耗,提高逆变效率。
1 现有无功电压控制策略
目前,常用的无功电压控制方法主要包括固定功率因数控制法(cosφ)、功率因数-有功控制法[cosφ(P)]、无功功率-电压控制方法[Q(V)]3种。
1.1 开环无功电压控制策略
cosφ法和cosφ(P)法均为开环的控制方法,其中:cosφ法以固定功率因数吸收一定的感性无功;cosφ(P)法根据逆变器输出的有功功率来调整功率因数或无功吸收量,如图1所示。
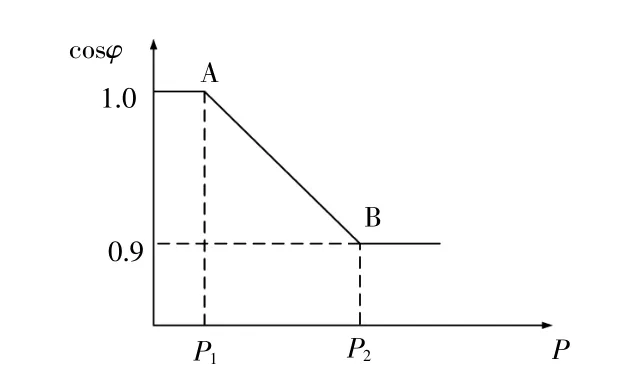
图1 cosφ(P)函数曲线示意图Fig.1 Diagram of cosφ(P)method
开环控制方法可以根据有功输出量P快速计算出无功吸收量Q,由于没有建立无功Q和并网点电压VPCC的直接关系,所以不能精准控制电压,在本地负载发生变化时,并网点电压控制效果会有明显偏差。
1.2 闭环无功电压控制策略
Q(V)法为典型的闭环控制算法,原理如图2所示。根据实测并网点电压VPCC实时调整无功输出Q,最终保证电压在允许范围内。
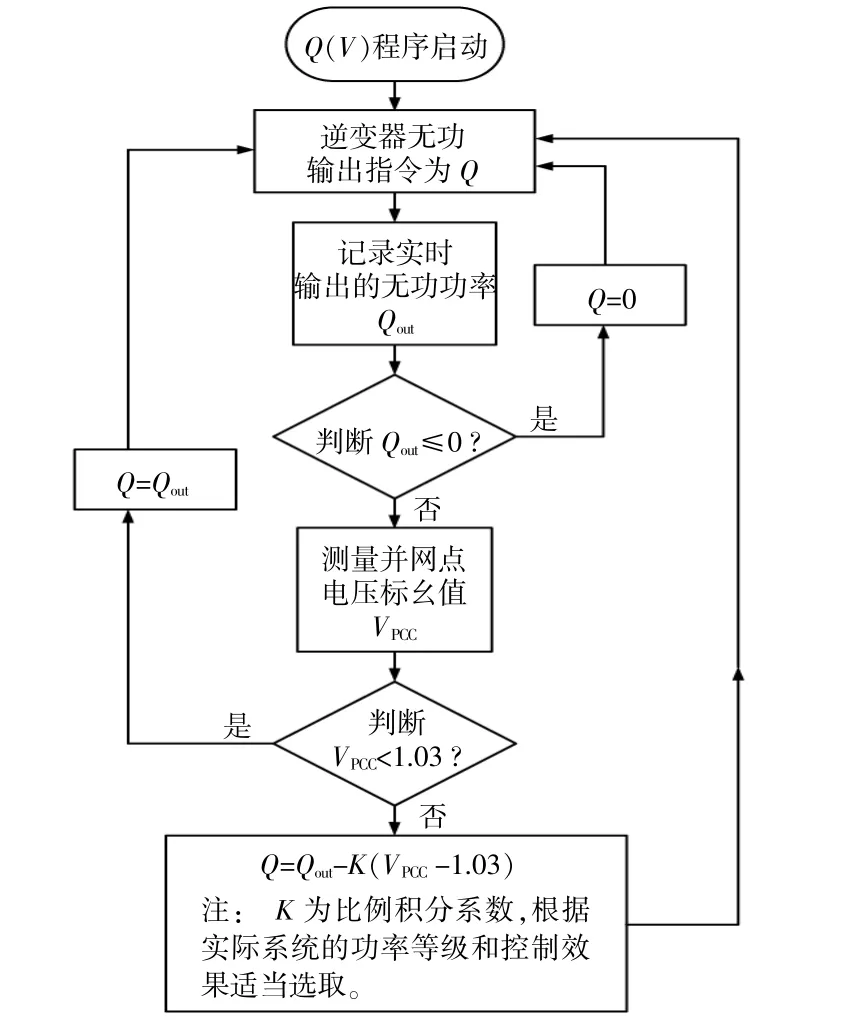
图2 Q(V)法流程图Fig.2 Flow chart of Q(V)method
由于建立了无功吸收量Q和并网点电压VPCC的直接关系,所以闭环控制方法在光照和负载变化的情况下,都可以很好地控制并网点电压。然而,由于电力系统结构负载复杂,且参数时变,传统闭环控制中的控制器(如PI控制器)会产生收敛时间长的问题。
2 自适应模型预测的无功电压控制算法
2.1 常规模型预测算法
模型预测算法是一种智能控制算法,它的总体思路是滚动优化[12]。根据优化指标,考虑当前时刻被控对象的预测模型,给出当前时刻的控制量u(k),控制量同时进入实际被控对象和被控对象的预测模型,分别得到下一时刻实际输出y(k+1)和预测输出y*(k+1),两者作差得到误差量c(k+1),该误差量作为修正下一时刻被控对象预测模型的依据,如图3所示[13]。
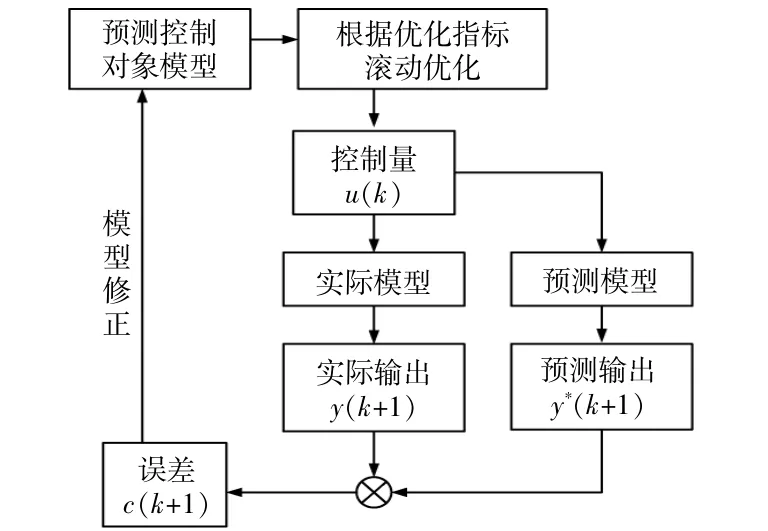
图3 模型预测算法Fig.3 Model prediction algorithm
电网模型的相关参数会随着分布式电源和负载的变化而改变,而模型预测算法恰恰能通过滚动优化实时修正模型,并保持最佳控制状态。近年来模型预测算法在智能微网控制中有了越来越多的应用。
2.2 光伏并网逆变器无功电压控制模型
分布式并网光伏逆变器通常工作在“本地消纳,余量上网”模式下,模型如图4所示。
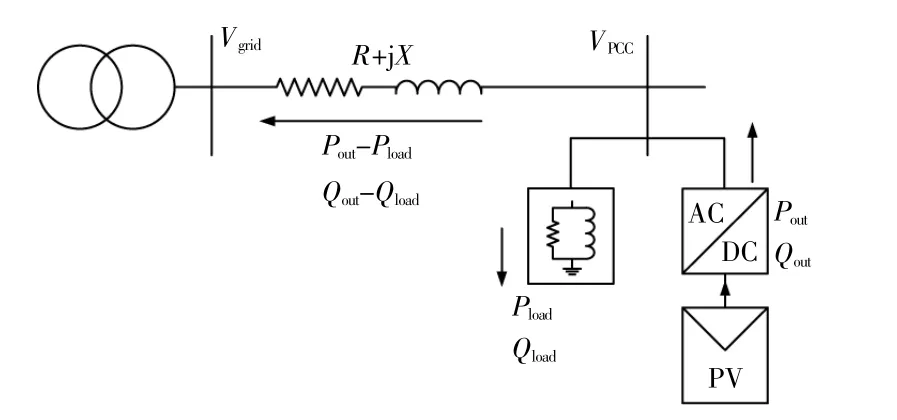
图4 无功电压控制模型Fig.4 Model of reactive power and voltage control
图中:Vgrid为理想电压源;R,X为等效线路阻抗;Pload,Qload为本地有功、无功负载;Pout,Qout为逆变器输出的有功、无功功率,当Qout为负时,逆变器吸收感性无功功率。
图4模型中,并网点电压升高ΔV为
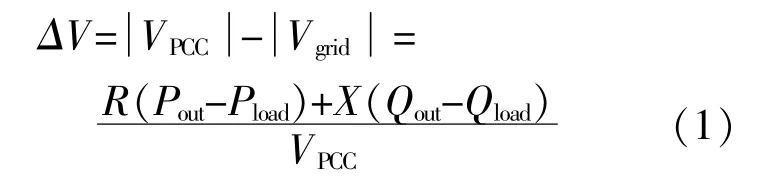
式中:ΔV为电压升高上限,为定值;通常分布式逆变器工作在MPPT模式,Pout直接受到光照影响,在不考虑弃光的情况下是不可控的;Pload,Qload为本地负载的有功、无功,逆变器同样不能控制,但可以通过传感器或其他通信手段将此信息传送到逆变器内参与运算;由线路实际阻抗、线路拓扑结构组成,并受到其他节点的负载情况影响,R,X在本地逆变器也无法控制;VPCC为并网点电压,可以由逆变器测量得到,变化范围比较小。通常,逆变器都可以四象限运行,即在满足视在功率上限的基础上,逆变器可以输出任意的Qout,所以Qout为逆变器唯一可以完全控制的量,无功电压算法也正是通过控制Qout来满足电压升高上限。
各参数特点如表1所示。

表1 各个参数的特点Table 1 Characteristics of each parameter
根据表1,将式(1)变形后可得:
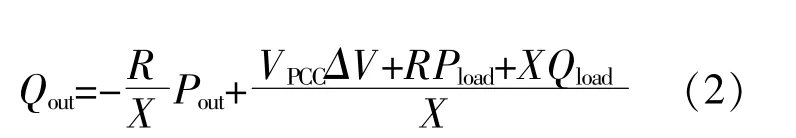
令:
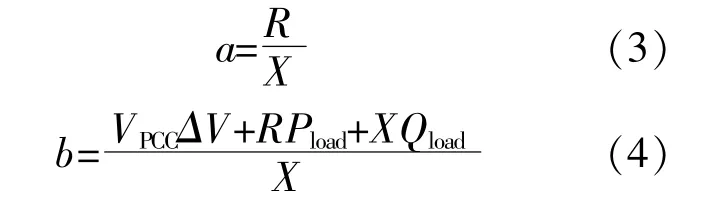
则式(2)可等效为

式中:a,b为系统的结构参数。
a,b的所有参数均为不变的量或短时间内为恒量,因此只要准确得到a,b值,就可以计算出无功吸收量Q,并将ΔV控制在限定范围内。
2.3 自适应模型预测算法
用滚动优化算法计算当前时刻的an和bn,将式(5)等效为直线解析式,采用当前时刻满足ΔV约束条件的(Pn,Qn)和上一时刻满足ΔV约束条件的(Pn-1,Qn-1)求解待定系数[22]~[26],具体表达式为
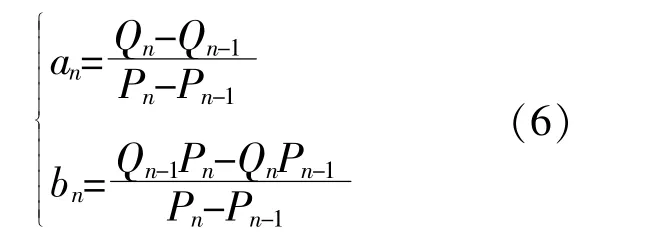
算法要考虑逆变器通过吸收感性无功来控制ΔV不越限,如果并网点电压没有达到ΔV上限,逆变器不须要输出感性无功来达到ΔV上限,具体方法如图5所示。
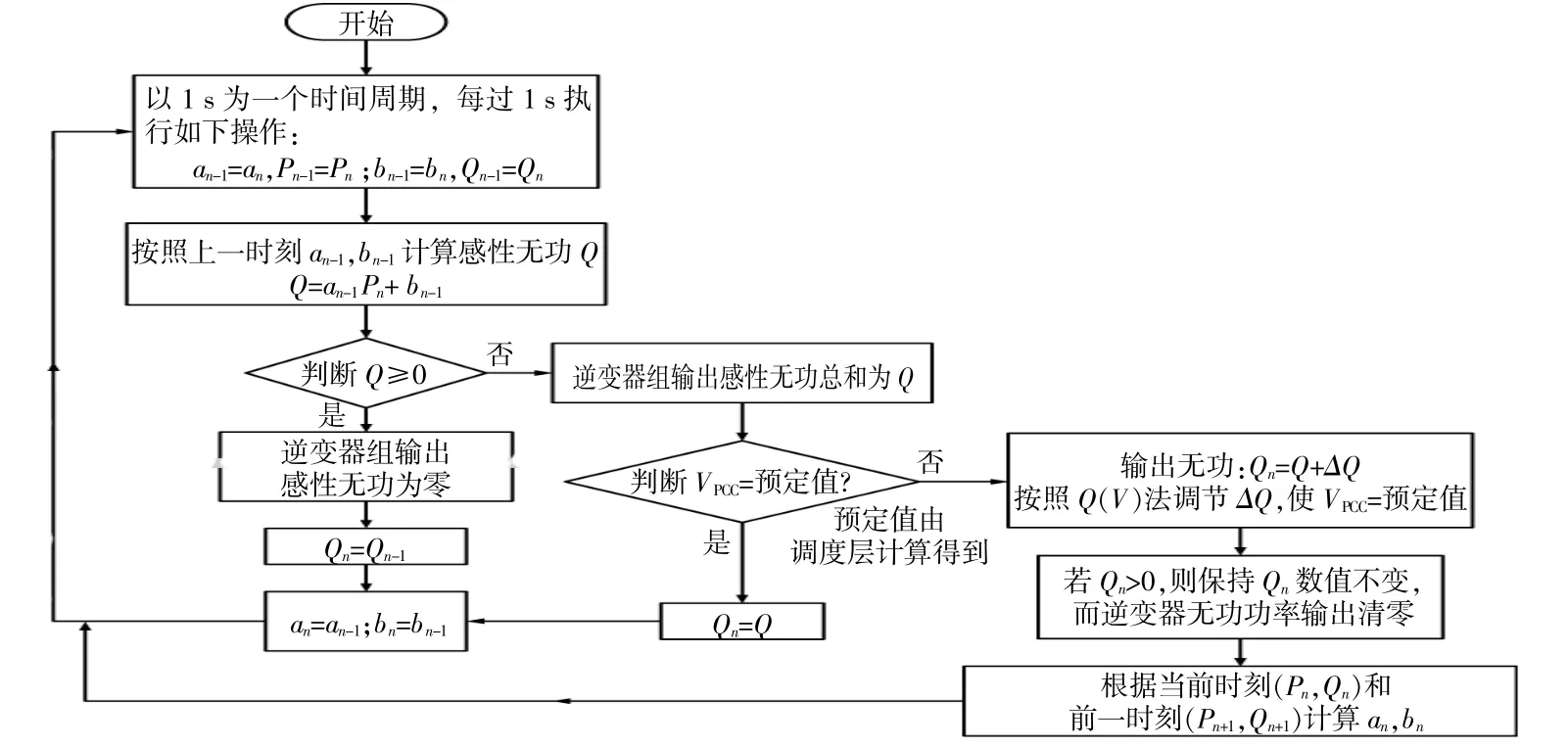
图5 基于自适应模型预测的无功电压控制策略Fig.5 Reactive power and voltage control strategy based on self-adapted model prediction control method
以1 s为一个时间周期,每个时间周期开始时,假设模型没有发生变化,根据上一个时间周期的模型参数an-1,bn-1和本时刻的有功功率输出Pn,可以计算出逆变器在模型不变的情况下,输出Qout。逆变器输出无功的目的是降低VPCC,所以应该吸收感性无功,即无功输出为负;计算得到输出Qout为正值时,说明此刻有功输出较小,尚不足以引起VPCC电压升高越限,所以不需要吸收无功,将上一时刻的参数直接刷新成为本时刻的参数,重回到算法的起点。如果计算得到应该吸收Q为负值,则说明逆变器输出的有功功率引起了电压升高越限,须要吸收感性无功,将ΔV控制在规定范围之内,逆变器按照计算值输出Qout。如果在误差允许范围内,VPCC等于调度层给出的预定值,即ΔV刚好没有越限,那么说明电网模型确实没有改变,此刻将逆变器的无功实际输出作为Qn,并刷新结构参数,返回算法起点。
如果输出无功Q,但是VPCC不等于预定值,无论其变大还是变小,都说明模型发生了变化,需要重新计算a,b。首先找到一个VPCC满足预定值的Qn;按照Q(V)法,通过电压反馈调节无功输出,如果电压超过上限,增加无功吸收量,如果电压低于上限,减少无功吸收量,直至不吸收无功。得到Qn后,可以与当前时刻的有功输出Pn构成一个点(Pn,Qn),与上一时刻对应的点(Pn-1,Qn-1)相加,按照式(6),二者共同参与计算,可以解出新的模型参数an,bn,然后回归算法起点,完成一次循环。
3 仿真与实验结果
3.1 仿真与实验参数
按照图4结构构件实验平台,并按照实际参数在Matlab/Simulink环境中搭建仿真平台,验证本文提出算法与传统算法的控制效果。实验和仿真主要参数如表2所示。其中在仿真过程中逆变器输出功率某一时刻由10 kW阶跃至12 kW;实物实验中迫于逆变器功率上限,输出功率有9 kW突变至8 kW。由于仿真和实验网络较小,引起ΔV升高不明显,故指定VPCC上限为额定电压的1.01 p.u.。
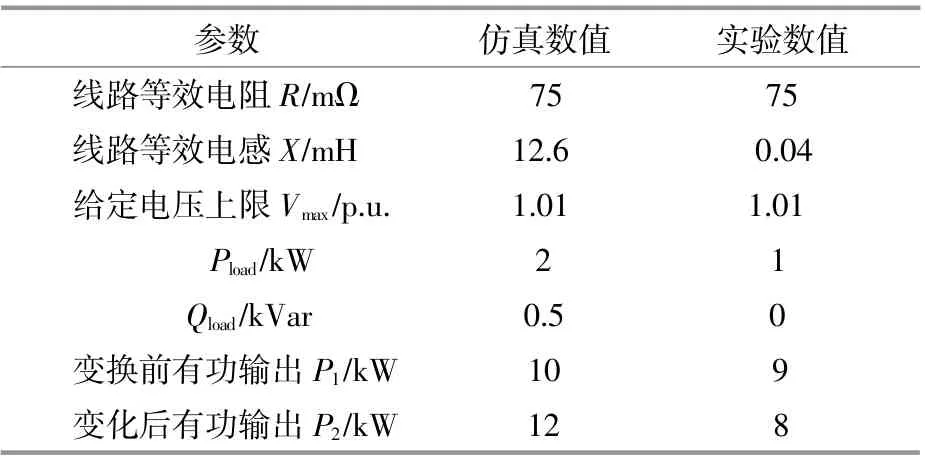
表2 仿真与实验参数Table 2 Simulation and experimental conditions
3.2 仿真结果
Q(V)控制法、自适应模型预测算法的逆变器输出有功、无功和电压标幺值曲线如图6,7所示。自适应算法主要参数通过系统自我修正,不必人为设定,而其他仿真条件参数与Q(V)法相同。
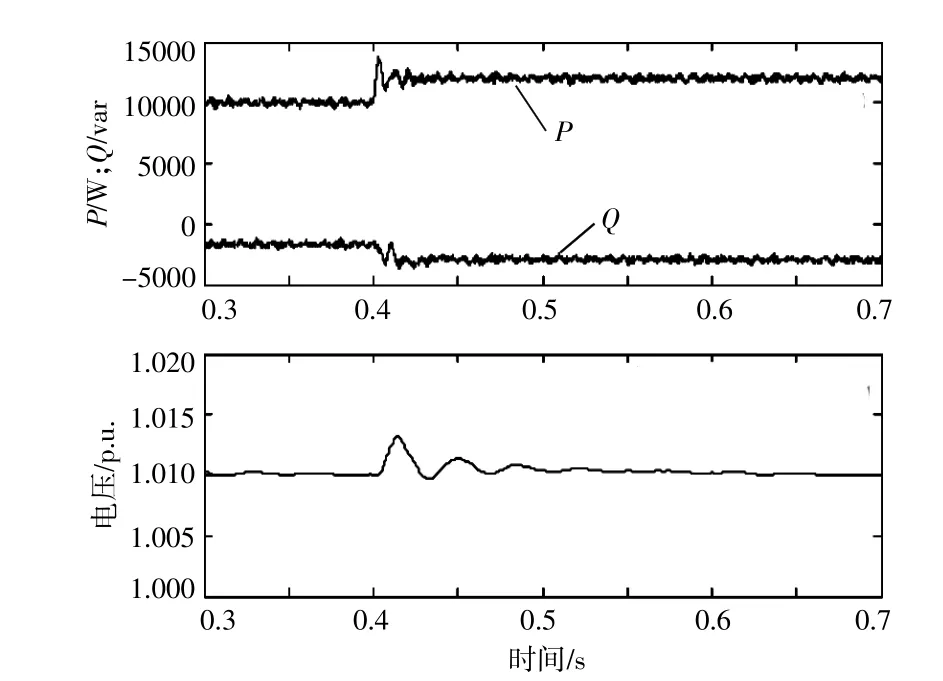
图6 Q(V)法的仿真结果Fig.6 Simulation results of Q(V)method
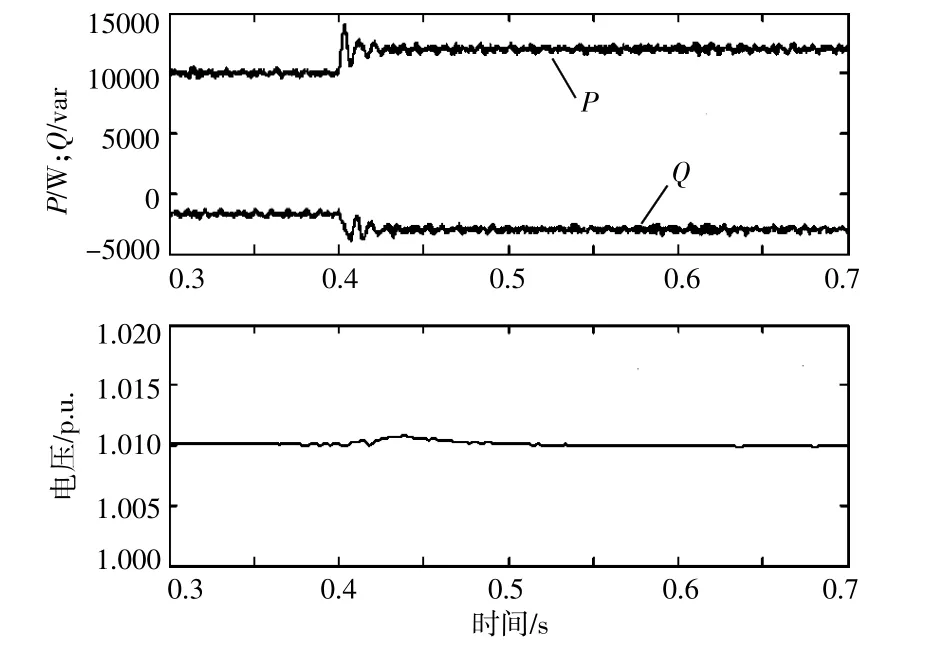
图7 自适应模型预测算法仿真结果Fig.7 Simulation results of Self-adapted MPCmethod
由图6,7可知:0.4 s,有功输出从10 kW阶跃至12 kW,应用Q(V)算法的电压经过几个波动后逐渐进入稳态。自适应模型预测算法校正准确后,可以看成一个开环控制,动态性能得到了大大提高,在有功发生突变时,自适应模型预测的无功电压控制电压超调明显变小,收敛速度更快。
3.3 实验结果
按照图4和表2中的参数进行实验,实验平台如图8所示。

图8 实验平台实物照片Fig.8 Physical picture of experiment platform
逆变器输出有功功率为9 kW,并自动匹配适当的无功功率吸收量来控制电压,以满足在ΔV上限。某一时刻令并网有功阶跃至8 kW,采用Q(V)法和模型预测算法的实验结果分别如图9,10所示。

图9 Q(V)法无功电压结果Fig.9 Experimental results of Q(V)method
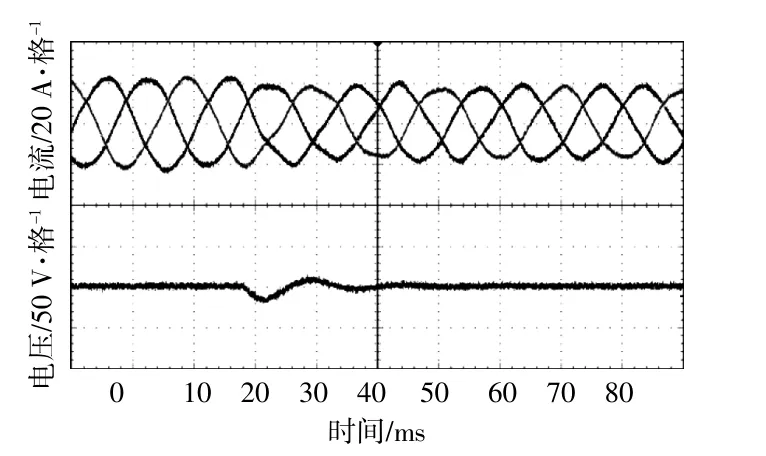
图10 自适应模型预测算法结果Fig.10 Experimental results of self-adapted MPCmethod
由图9,10可知:自适应模型预测算法的电压超调量远远小于Q(V)法,前者大约是后者的1/4;自适应模型预测的响应时间比Q(V)法极大缩短,前者约一个工频周期后电压就不在振荡,而后者持续振荡超过3个工频周期;在有功阶跃的一段时间内,二者都须要调节有功和无功电流,所以在过渡周期存在一定的电流畸变。自适应模型预测算法在略多于一个工频周期后,输出电流就恢复了原来的电能质量,而Q(V)法经过3个工频周期,输出电流仍在变化。由实验结果可以看出,在无功电压控制方面,自适应模型预测控制算法的动态性明显优于Q(V)法。
4 结束语
传统无功电压控制方法存在一定缺陷,本文建立光伏逆变器并网电压物理和数学模型,引入自适应模型预测算法,在无功电压控制模型加入自适应环节,形成自适应模型预测算法,通过滚动优化得到合适的结构参数。实验结果表明,本文所提出的基于自适应模型预测算法的无功电压控制策略,其响应速度和控制精度均优于Q(V)法。
