大型风力机变桨距加载系统流量补偿方法研究

2021-08-23程明杰方占萍李玉宏

可再生能源 2021年8期

甄亮，党坤，程明杰，方占萍，李玉宏

（酒泉职业技术学院甘肃省太阳能发电系统重点实验室，甘肃酒泉 735000）

0 引言

风力机变桨距控制是提高发电效率和电能质量的有效途径之一，也是大型风力发电机组控制的关键技术。目前，国内外学者对大型风力机变桨距控制系统做了大量的研究。郑大周[1]针对直驱式风力发电机组设计了一种不依赖于准确数学模型、抗干扰能力强且易于实现的风力发电机组变桨距自抗扰控制器。任海军[2]设计了基于人工蜂群-RBF-PID的风力机液压变桨距控制系统。闫学勤[3]针对风力机独立变桨设计了基于科尔曼坐标变换的改进型准比例积分谐振（IQPI-R）控制策略和将叶片方位角权系数分配与叶片根部气动载荷反馈相结合的独立变桨距控制方法（AAWCLF）。

以上研究均采用各种控制策略提高风力机变桨距系统的控制效果，而针对大型风力机变桨距加载系统的研究甚少。魏列江[4]在实验室内搭建了大型风力机变桨距半实物仿真系统，分析了间隙大小对动态加载系统性能的影响，但没有分析加载过程中多余力的抑制方法。林勇刚[5]搭建了风力机变桨距半物理仿真试验台，分析了变桨距的静态加载，但没有考虑动态载荷的影响。针对加载系统多余力抑制方法的研究主要集中在控制策略的优化和改进。Shuo Kang[6]针对含有机械间隙的电液负载模拟器的力控制系统，提出了一种ADD干扰解耦控制策略。Chenghu Jing[7]对执行器运动干扰、参数不确定性和未建模动态对加载系统的影响进行了分析。文献[8]，[9]分析了负载刚度、惯性等对加载系统的影响。

以上学者对动态加载系统控制策略做了深入研究，而针对大型风力机变桨距动态加载系统多余力的研究甚少。本文通过理论分析和数值仿真相结合的方法，对大型风力机变桨距动态加载系统产生多余力的过程、机理以及抑制方法作了深入的研究，提出了采用压力伺服阀-流量伺服阀双阀并联结构来抑制加载系统产生多余力的方法。

1 物理建模

本文研究的大型风力机变桨距系统是典型的液压变桨，根据变桨距驱动形式等效为一个位置系统。叶片变桨距负载加载系统是一个典型的力系统，其简化的结构原理如图1所示。由图1可知：左边为风力机叶片变桨距位置系统，系统中的位移传感器的实时反馈构成了一个实时位置闭环系统，根据自然风信号给定指令信号驱动风力机叶片变桨距负载运动；右边为加载系统，加载系统中由一个压力伺服阀和一个流量伺服阀并联控制液压缸输出力，从而对叶片变桨距负载进行加载。由于叶片变桨距负载的主动运动，对加载系统在位置上产生了干扰，加载液压缸两腔产生了一个强迫流量，导致加载液压缸两腔产生压力差，即产生了多余力。多余力的存在影响加载系统的力跟踪性能，尤其在叶片变桨距负载开始运动、停止、换向、加速以及减速时产生的多余力很大。

图1 大型风力机变桨距负载加载系统等效结构原理图Fig.1 Schematic diagram of the equivalent structure of the variable-pitch loading system of a large wind turbine

2 叶片变桨距负载加载系统数学建模

为了减小由于叶片变桨距负载的主动运动产生的强迫流量，本文提出压力伺服阀-流量伺服阀双阀并联控制方案，即在控制加载液压缸的两腔压力的压力伺服阀基础上，并联一个流量伺服阀。流量伺服阀将产生的强迫流量转移到加载缸的另一腔，从而减小流量波动，进而抑制多余力的干扰，使得压力伺服阀在流量伺服阀的补偿作用下，近似工作在主动加载的状态下。

并联流量伺服阀后，系统的结构发生了变化。由于叶片变桨距位置扰动产生的流量波动由流量伺服阀补偿，加载系统需要的流量来自于压力伺服阀，因此，压力伺服阀和流量伺服阀是典型的并联结构。

2.1 压力伺服阀控制系统建模

单独从叶片变桨距负载加载系统考虑，系统模型由压力伺服阀流量方程、加载液压缸流量连续性方程、作用力平衡方程和加载系统输出力方程组成。

单阀加载系统的压力伺服阀的线性化流量方程为

式中：QLD为压力伺服阀的负载流量，m3/s；KqD为压力伺服阀的流量增益，m2/s；XvD为压力伺服阀的阀芯开口量，m；KcD为压力伺服阀的流量-压力系数，m5/（N·s）；PLD为液压缸的负载压力，N/m2。

单阀加载系统的液压缸的流量连续性方程为

式中：QLF为压力伺服阀的负载流量，m3/s；PLF为压力伺服阀的负载压力，N/m2；AF为液压缸活塞有效面积，m2；yF为液压缸活塞位移，m；CtcF为液压缸的总泄漏系数，m5/（N·s）；VtcF为单阀加载液压缸两腔的总容积，m3；βe为液压油的等效体积弹性模数，Pa。

式中：CicF，CecF分别为单阀加载液压缸的内、外泄露系数。

单阀加载系统作用力平衡方程为

式中：mF为液压缸有效活塞质量，kg；BcF为液压缸活塞和负载等效的粘性阻尼系数，N·s/m；Fg为单阀加载系统的输出力，N。

单阀加载系统的输出力方程为

式中：Ke为系统力传感器的弹性刚度，N/m；yF为液压缸的活塞位移，m。

近似认为负载位移与加载液压缸位移相等，即yF≈yL，忽略BCF可得仅有压力伺服阀控制系统的方块图（图2）。

图2 压力伺服阀控制的系统方块图Fig.2 System block diagram of pressure servo valve control

图2中，KaF为叶片变桨距位置系统伺服放大器系数。

加载系统的压力伺服阀受到流量波动的干扰，尤其在叶片变桨距负载开始运动、换向和停止时，干扰尤为突出，从压力伺服阀控制系统方块图得到强迫流量QD为

式中：KL为叶片变桨距负载等效刚度，N/m；mL为叶片变桨距负载和加载缸等效质量，kg；YD为叶片变桨距负载位置系统液压缸的位移，m；s为拉氏变换因子。

根据加载系统多余力产生机理分析，强迫流量是加载系统的多余力产生的主要原因，用单一的压力伺服阀控制加载缸时，很难既满足压力，又能补偿产生的强迫流量。因此，为了减小产生的强迫流量，尽量选择理想的压力伺服阀，实际上，压力伺服阀的输出压力与负载流量存在必然的关系。压力伺服阀的压力与流量的关系为

式中：K01为压力伺服阀负载腔锁闭时的压力增益，N/m3；i为压力伺服阀的输入电流，A；K02为压力伺服阀输出压力为零处的流量-压力系数，m5/（N·s）；T为与负载有效流量及油液可压缩性流量等有关的时间常数，s；QLP为压力伺服阀输出的负载流量，m3/s；ωPSV为压力伺服阀的动态响应频率，Hz；ζPSV为压力伺服阀的阻尼比，无因次。

2.2 压力伺服阀-流量伺服阀双阀并联控制系统建模

风力机变桨距系统的性能直接影响叶片偏转的快速性、准确性，本文利用加载系统模拟风力机叶片上承受的任意风载荷。保证加载系统实时跟踪给定的风信号，消除由强迫流量产生的多余力，才能可靠地控制风力机叶片变桨距。而根据前文分析的只有压力伺服阀控制系统，在力加载过程中，产生了QD，因此只要将产生的QD补偿，叶片变桨距负载加载系统的压力伺服阀就能工作在理想状态。

双阀并联加载系统流量伺服阀的线性化流量方程为

式中：QLF为双阀并联加载系统流量伺服阀的负载流量，m3/s；Kqj为双阀并联加载系统流量伺服阀的流量增益，m3/s；XVj为双阀并联加载系统流量伺服阀阀芯的开口量，m；KCj为双阀并联加载系统流量伺服阀流量-压力系数，m5/（N·s）；PLF为双阀并联加载系统压力伺服阀的负载压力，N/m2。

双阀并联加载系统的流量连续性方程为

式中：YF为双阀并联加载液压缸的位移，m；VtF为双阀并联加载液压缸的总容积，m3；βe为液压油的等效体积弹性模数，Pa。

双阀并联加载系统作用力平衡方程为

式中：BCF为双阀并联加载液压缸的粘性阻尼系数，N/（m/s）；mF为双阀并联加载液压缸的质量，kg；mL为叶片变桨距负载和加载缸等效质量，kg。双阀并联加载液压缸输出力平衡方程为

双阀并联加载系统输出压力方程为

采用双阀并联控制，用流量伺服阀控制叶片变桨距负载YF，压力伺服阀控制叶片变桨距负载Fg，可得到：

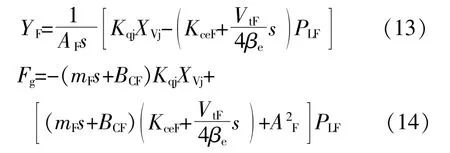
2.3 叶片变桨距负载加载系统强迫流量补偿

为保证叶片变桨距负载加载系统的压力伺服阀输出的压力不受产生的强迫流量扰动，须要保证流量伺服阀的输出流量为QD，如此，压力伺服阀便工作在理想状态。

由式（11）可得：

在叶片变桨距负载加载系统中，由于叶片变桨距负载可以等效为质量-弹簧系统，在实际风力机中，叶片变桨距负载的位置变化很小。从式（15）可以看出，YF是一个二阶振荡环节，二阶振荡环节作为流量伺服阀输入信号比较复杂，一般简化计算，简化计算得到的流量伺服阀的输入信号为

从而得到双阀并联控制的系统方块图（图3）。

图3 双阀并联控制系统方块图Fig.3 Double valve parallel control system block diagram

3 仿真及结果分析

3.1 压力伺服阀控制仿真分析

在MATLAB的Simulink中搭建如图2所示的压力伺服阀控制的系统仿真模型。对叶片变桨距负载位置系统分别施加不同频率和幅值的正弦信号，得到由强迫流量造成的多余力；对加载系统分别输入不同频率和幅值的正弦信号。比较产生的多余力，分析正弦信号的频率对输出的力信号的影响。

图4为叶片变桨距负载位置系统施加频率为5 Hz，幅值为±5 mm正弦信号，加载系统输入频率为5 Hz，幅值为±180 N正弦信号时的跟踪曲线。

图4 压力伺服阀控制负载为5 Hz，加载信号为5 Hz的跟踪响应Fig.4 Pressure servo valve controls load 5 Hz，load signal 5 Hz tracking response

由图4可知，输出力幅值产生一定的衰减，相位有很大的滞后，不能实现点点跟踪，这就是叶片变桨距负载主动运动产生的多余力造成的结果，需要补偿措施。

图5为叶片变桨距负载位置系统施加频率为10 Hz，幅值为±5 mm正弦信号，加载系统输入频率为5 Hz，幅值为±180 N正弦信号的输出曲线。图6为叶片变桨距负载位置系统施加频率为10 Hz，幅值为±5 mm正弦信号，加载系统输入频率为10 Hz，幅值为±180 N正弦信号的输出曲线。

图5 压力伺服阀控制负载为10 Hz，加载信号为5 Hz的跟踪响应Fig.5 Pressure servo valve controls load 10 Hz，load signal 5 Hz tracking response

图6 压力伺服阀控制负载为10 Hz，加载信号为10 Hz的跟踪响应Fig.6 Pressure servo valve controls load 10 Hz，load signal 10 Hz tracking response

由图5与图6比较可知：随着叶片变桨距负载运动频率增大，输出力曲线严重失真；随着加载系统输入信号频率的增大，输出力曲线严重失真。

随着叶片变桨距负载运动频率的增大，加载系统输入信号频率和幅值的增大，输出力信号明显跟踪不上输入信号，严重失真。随着加载系统输入频率的增大，由叶片变桨距负载主动运动产生的多余力增大，严重影响加载系统的跟踪性能和其他动态性能指标，因此，须要采用相应的补偿措施和控制策略来消除产生的多余力。

3.2 压力伺服阀-流量伺服阀双阀并联控制仿真分析

根据图3所示双阀并联控制系统方块图，对叶片变桨距负载和加载系统输入信号分别施加不同频率和幅值，与单阀控制系统的仿真结果相比较，分析加载系统输出力的跟踪情况。

图7为叶片变桨距负载位置系统施加频率为5Hz，幅值为5mm正弦信号，加载系统输入频率为5 Hz，幅值为180 N正弦信号的输入和输出对比曲线，以及产生的多余力曲线图。比较图7与图4可知，双阀并联控制输出曲线很好地跟踪了输入信号，在幅值上和相位上都得到很大的改善。

图7 叶片变桨距负载为5 Hz，加载系统输入为5 Hz的跟踪响应Fig.7 Blade variable pitch load 5 Hz，loading system 5 Hz tracking response

图8为叶片变桨距负载位置系统施加频率为10 Hz，幅值为±5 mm正弦信号，加载系统输入频率为5 Hz，幅值为180 N正弦信号的输入和输出对比曲线，以及产生的多余力曲线。

图9为叶片变桨距负载位置系统施加频率为10 Hz，幅值为±5 mm正弦信号，加载系统输入频率为10 Hz，幅值为±180 N正弦信号的输入和输出对比曲线，以及产生的多余力曲线。

图9 叶片变桨距负载为10 Hz，加载系统输入为10 Hz的跟踪响应Fig.9 Blade variable pitch load 10 Hz，loading system 10 Hz tracking response

由图8，9可知：随着施加在叶片变桨距负载位置系统的频率和加载系统输入信号频率的增大，加载系统输出力对输入信号的跟踪性能明显下降，在加载频率增大到10 Hz时，产生的多余力小于给定输入的10%；叶片变桨距负载的主动运动对加载系统产生的多余力，随着施加在叶片变桨距负载位置系统的频率和加载系统输入信号的频率增大而增大。