风力机翼型表面凸台的粗糙度效应研究
2021-08-23耿海超余海洋罗大海
耿海超,余海洋,罗大海
(上海理工大学 能源与动力工程学院,上海 200093)
0 前言
在风力机实际运行中,受周围环境的影响,风力机叶片表面将附着污垢、灰尘、昆虫尸体等污染物。随着时间的增长,叶片表面污染物增多,导致叶片表面粗糙度增加,降低了叶片的气动性能,影响风力机功率输出[1],[2]。叶片表面粗糙度是影响风力机功率特性的重要因素之一,国内外研究者对叶片表面粗糙的风力机翼型的气动性能进行了数值模拟与实验研究。有研究表明,随着翼型表面粗糙度增加,翼型升力下降、阻力增大,风力机输出功率降低[3]。Soltani M R通过研究发现,翼型的气动性能对表面污染敏感,相比光滑翼型,粗糙翼型的失速攻角提前,最大升力系数降低了35%[4]。张骏通过数值模拟研究了风力机叶片表面积灰和昆虫尸体引起的粗糙度效应,发现前缘粗糙度严重影响了翼型的气动性能,而在尾缘布置一定的粗糙度却有积极的作用[5]。刘洪鹏采用XFOIL软件研究了最大相对厚度、最大相对弯度及尾缘厚度对翼型前缘粗糙度敏感性的影响,研究发现,翼型的最大相对厚度对所有的敏感性指标均产生显著性影响,而最大相对弯度和尾缘厚度仅对其中一些指标产生明显的影响[6]。
以上研究主要是通过风洞实验分析粗糙度对翼型气动性能的影响,较少采用数值模拟方法系统分析翼型表面的粗糙度效应。在数值模拟方面,关于粗糙度的RANS模拟,大多基于等效颗粒粗糙度高度的概念,同时选用全湍流模型,较少考虑翼型表面的流动转捩,数值模型的合理性也未得到充分验证。本文采用CFD方法,在翼型表面布置矩形凸台模拟粗糙度效应,通过数值仿真和流场显示分析粗糙度对风力机翼型气动特性的影响。
1 数值方法
本文基于ANSYSFluent软件对风力机翼型绕流流场进行二维定常不可压RANS模拟。速度压力耦合采用SIMPLE算法,压力项和动量项空间离散采用二阶迎风格式,同时考虑翼型表面的流动转捩。
1.1 γ-Reθt转捩模型
γ-Reθt模型与SST k-ω湍流模型结合形成的四方程模型Transition SST已经集成在ANSYS Fluent软件之中。该转捩模型由Menter F R[7]提出,由间歇因子γ和动量厚度雷诺数Reθt两个输运方程构成,考虑了自然转捩、旁路转捩及分离诱导转捩等多种转捩机制,在低速翼型流动转捩的预测方面可以给出准确的结果[8]。
γ的输运方程为
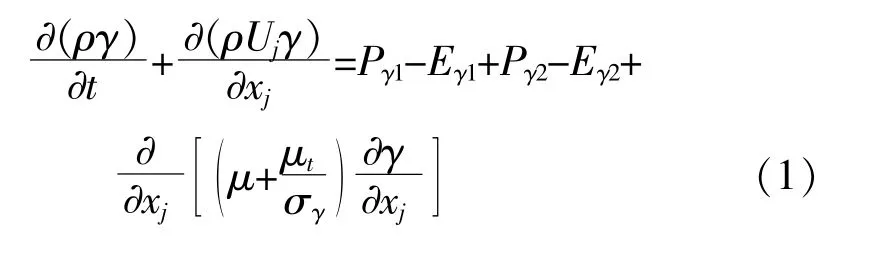
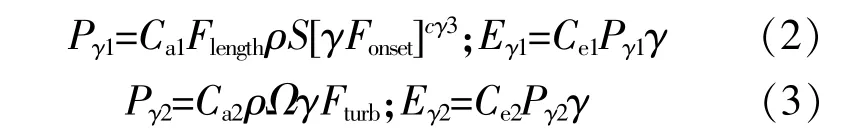
式中:μ为动力粘度;μt为湍流粘性系数;S为应变率;Ω为涡量;Flength为转捩区长度;Fonset,Fturb均为转捩控制函数;Uj为流体沿xj方向的速度分量;ρ为来流密度;Ca1,Ca2,Ce1,Ce2和σγ均为转捩模型常数;Pγ1,Eγ1,Pγ2和Eγ2均为转捩源项。
Reθt的输运方程为

1.2 几何模型、计算网格及边界条件
本文考虑的风力机翼型为DU91-W2-250和NACA63-425(图1),其常用于大型风力机叶片中部,翼型最大厚度均为弦长的25%。
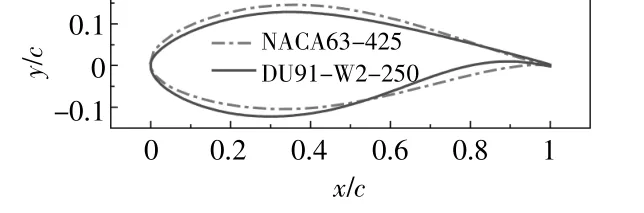
图1 翼型几何外形对比Fig.1 Airfoil geometry comparison
翼型弦长c为0.6 m,基于弦长的来流雷诺数Re为3×106。全局采用结构网格,计算域外边界距翼型表面约为40c。进口为速度入口,出口为压力出口边界条件,来流湍流强度设为0.07%,湍流粘度比为10,γ为1。翼型表面为绝热无滑移固壁,壁面附近第一层网格高度设为5×10-6m,保证y+≈1,近壁面法向网格增长比控制在1.1以内,翼型附近网格如图2所示。

图2 光滑DU91-W2-250翼型附近网格Fig.2 Grid near the DU91-W2-250 airfoil
对于粗糙翼型,为了与实验数据进行对比[9],在上翼面5%弦长处设置矩形凸台来模拟翼型表面粗糙度效应(图3)。

图3 粗糙DU91-W2-250翼型凸台附近网格Fig.3 Grid near the rough DU91-W2-250 airfoil boss
选用DU 91-W2-250翼型进行网格无关性验证,采用3种不同数目的网格来验证网格无关性,网格数分别为3万、6万和12万。网格无关性验证结果如图4所示。
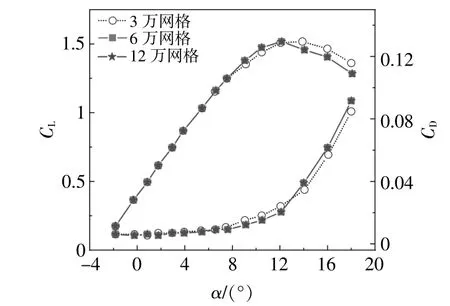
图4 网格无关性验证Fig.4 Grid independence verification
由图4可知,当计算所用网格量为6万时,计算所得到的翼型升力系数CL和阻力系数CD不再随网格的增大而发生变化,说明此时计算结果与网格无关。因此后续计算所用网格翼型周向和法向的网格数为371×121,网格量为6万。
1.3 计算方法验证
图5,6分别为NACA 63-425和DU 91-W2-250翼型的计算结果和实验数据对比。由图5(a)可知,当攻角α小于8°时,计算的CL和CD均与实验数据吻合较好;在最大CL对应的α附近以及失速以后,计算结果存在一定误差。对于粗糙翼型,实验中采用锯齿形粗糙带,布置在翼型上表面5%弦长处,粗糙带长度为12 mm,高度为0.35 mm,为了使模拟结果尽可能和实验值保持一致,在CFD模拟中选取的矩形凸台的长度为12 mm,高度为1~3 mm。由图5(b)可知:相较于过大或过小的矩形凸台高度,当凸台高度为2 mm时,计算的CL和CD值总体上与粗糙翼型实验数据更为接近;对比矩形凸台高度和锯齿形粗糙带的高度,尽管两者有较大差别,但大范围攻角下的计算结果与实验数据较为吻合,这也从侧面说明了在翼型表面粗糙度效应分析中用矩形凸台代替锯齿形粗糙带的方案是可行的。
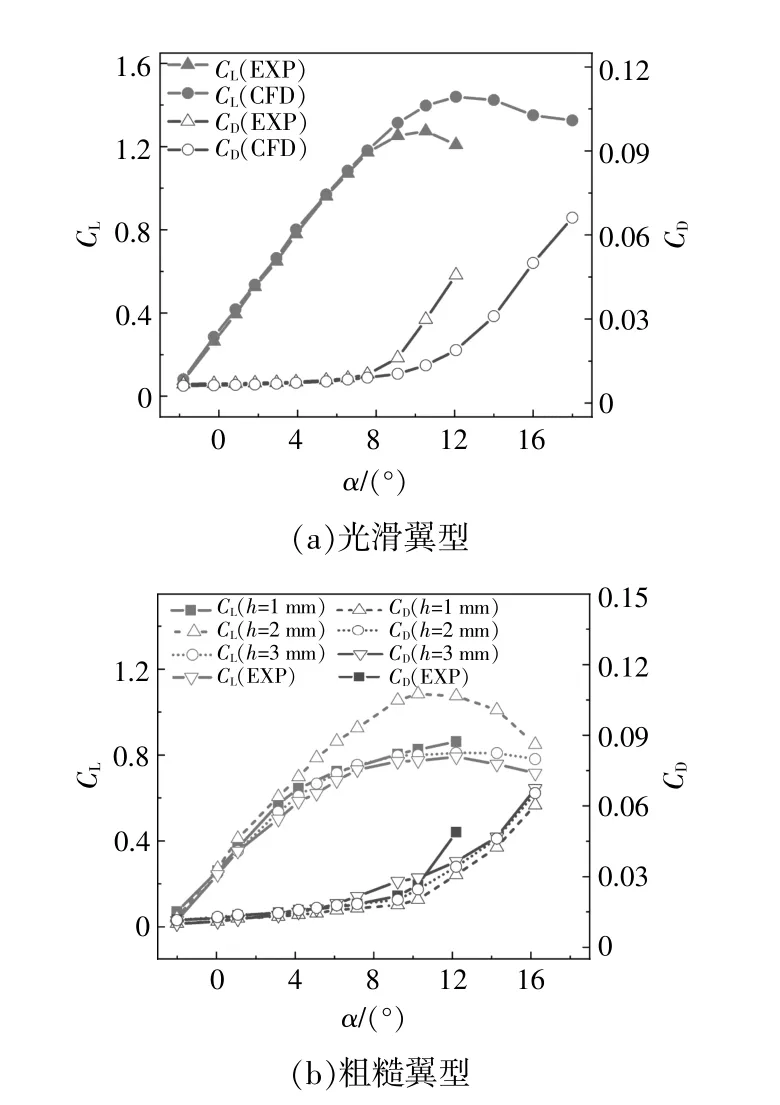
图5 NACA63-425翼型升、阻力系数与实验数据对比Fig.5 Comparison of NACA63-425 airfoil lift and drag coefficient with experimental data
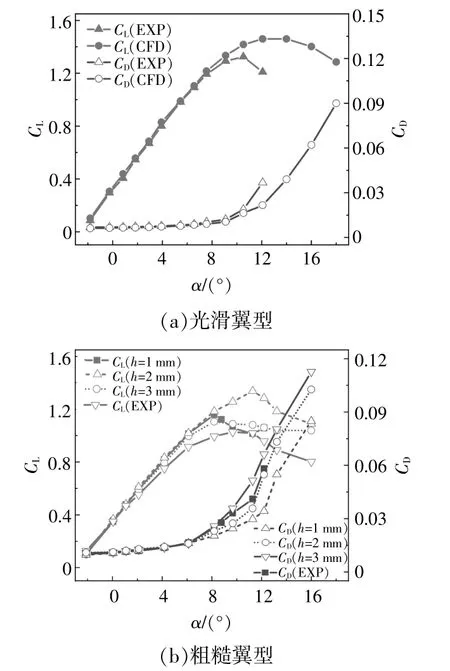
图6 DU91-W2-250翼型升、阻力系数与实验数据对比Fig.6 Comparison of DU91-W2-250 airfoil lift and drag coefficient with experimental data
图7为不同α下DU91-W2-250光滑翼型表面压力系数Cp分布曲线。由图7可知,当α为6.7°和9.2°时,Cp计算值和实验值非常接近。
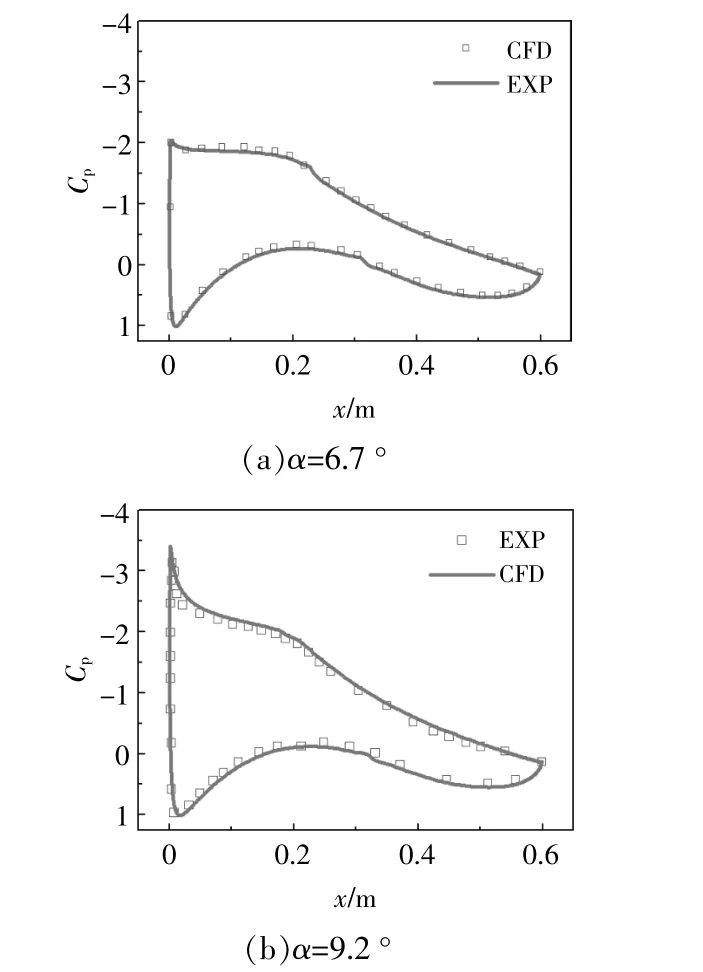
图7 光滑翼型表面压力系数分布Fig.7 Smooth airfoil surface pressure coefficient distribution
通过CL和CD的对比,以及翼型表面Cp分布的对比,总体上看来,本文的计算结果与实验数据吻合较好,说明本文所采用的计算方法是合理的。此外,从粗糙翼型的计算结果可知:在较大的凸台高度下,翼型的气动性能相比于原始翼型有明显的降低,NACA63-425翼型表现尤为显著;在翼型表面布置合适高度的矩形凸台,大体上可以等效于在翼型表面布置锯齿形粗糙带。
2 矩形凸台的粗糙度效应分析
2.1 不同凸台高度对翼型气动性能的影响
通过设置不同凸台高度来反映粗糙度对翼型气动性能的影响,凸台长固定为12 mm,布置在翼型吸力面5%弦长位置。随着凸台高度的增加,可以认为翼型表面粗糙度是逐渐增大的。对于NACA63-425光滑翼型,CL和CD的计算值在α>8°后与实验存在一定偏差;对于DU91-W2-250光滑翼型,CL和CD的计算值在α>10°后与实验存在一定偏差。为了尽可能减小计算误差的影响,在分析凸台高度对翼型气动性能影响时,对于NACA63-425和DU91-W2-250这两种翼型,考虑的α分别为7°和9°。
图8为不同凸台高度对NACA63-425翼型和DU91-W2-250翼型CL和CD的影响曲线。
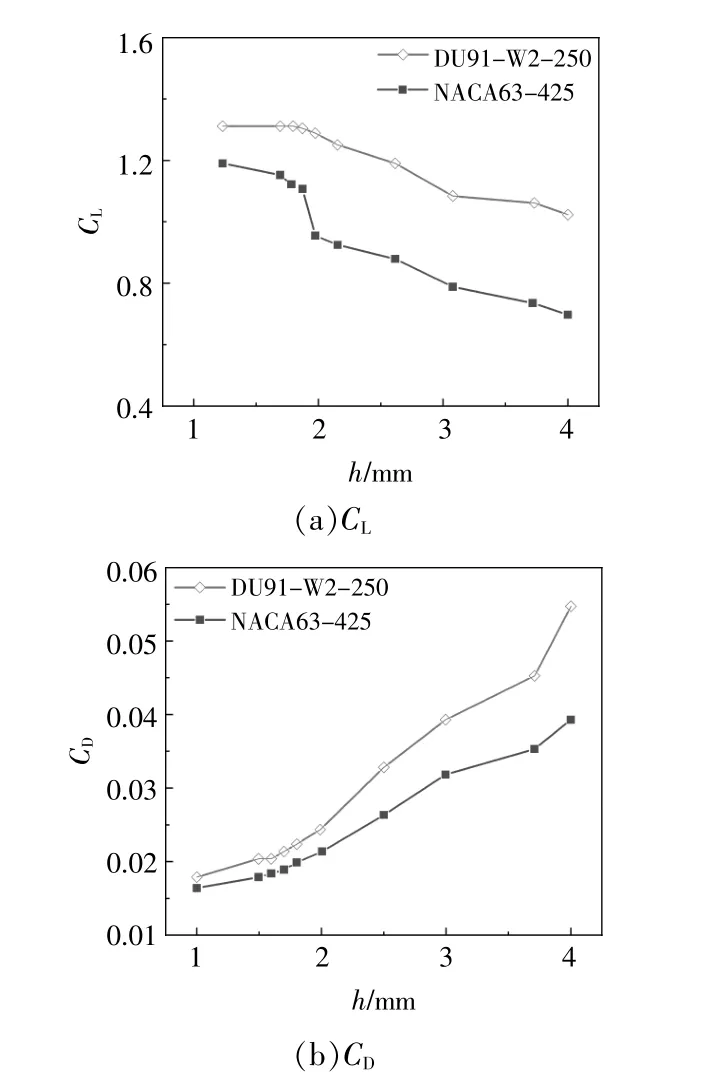
图8 不同凸台高度对翼型气动性能的影响Fig.8 Influence of different boss heights on aerodynamic characteristics of airfoil
由图8可知:随着凸台高度的增加,这两种翼型的CL均逐渐降低,CD均逐渐增大;NACA63-425翼型和DU91-W2-250翼型对表面粗糙度的感受特性不同,当凸台高度较小(h<0.8 mm)时,与光滑状况(h=0)相比,DU翼型的CL和CD变化较小,而NACA翼型的CL随凸台高度的增加急剧降低;当凸台高度较大(h>0.8 mm)时,粗糙翼型的气动性能相比光滑状况时明显降低。
图9,10分别为NACA63-425翼型和DU91-W2-250翼型在不同凸台高度下的绕流流线。
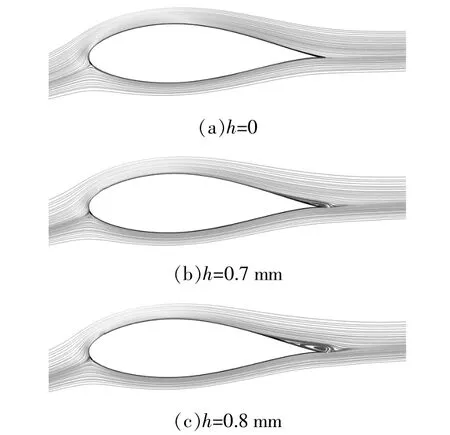
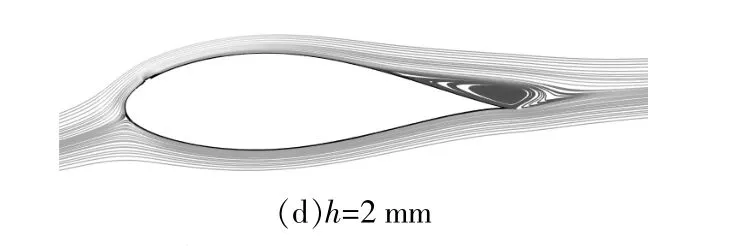
图9 不同凸台高度下NACA 63-425翼型绕流流线图(α=7°)Fig.9 Surface flow lines of NACA 63-425 airfoil around different heights(α=7°)
由图9可知,当凸台高度较小时(h=0.7 mm),NACA63-425翼型吸力面尾缘出现小的分离区,随着凸台高度的增加(h=0.8 mm),吸力面尾缘的分离区迅速扩大,引起CL的陡降,这也说明了NACA翼型的气动性能对粗糙度变化的感受特性是较为敏感的。由图10可知,对于DU91-W2-250翼型,当h从0.7 mm增大到0.8 mm时,吸力面尾缘的分离区范围略微增加,变化并不明显。
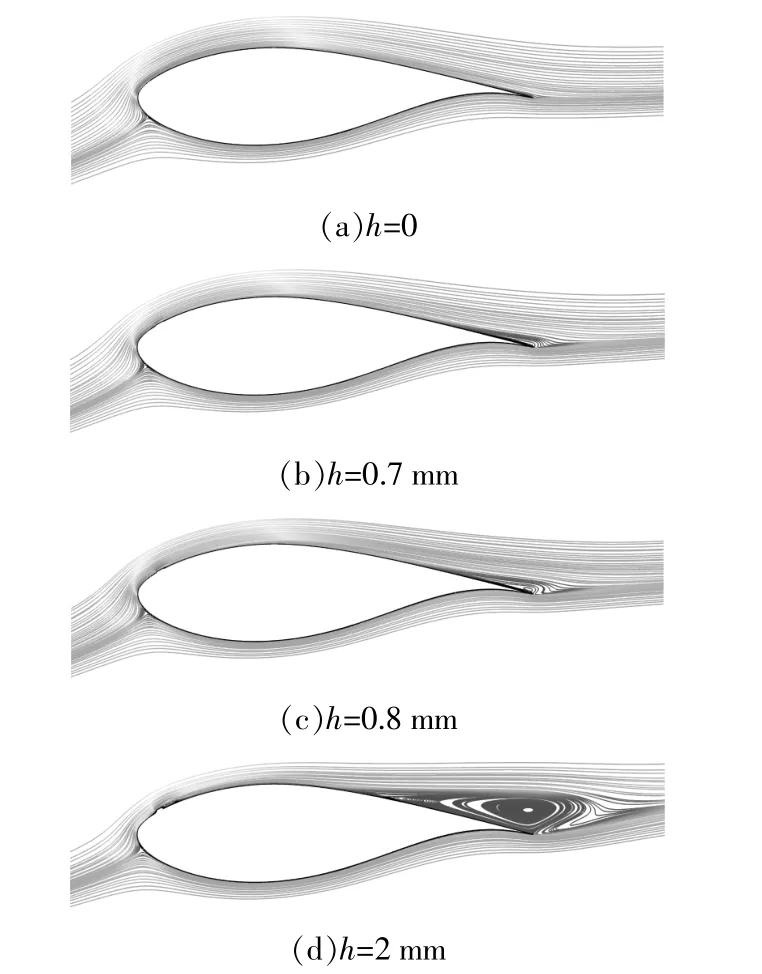
图10 不同凸台高度下DU91-W2-250翼型绕流流线图(α=9°)Fig.10 Surface flow lines of DU91-W2-250 airfoil around different heights(α=9°)
图11为DU91-W2-250翼型在不同凸台高度下的翼型表面转捩位置图。
由图11可知,凸台高度增加后,翼型压力面和吸力面的转捩位置没有明显变化,这也验证了当粗糙度较小时,DU翼型的CL和CD对粗糙度变化不敏感。
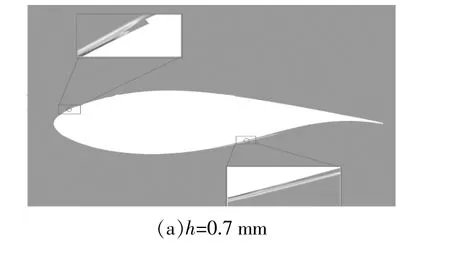
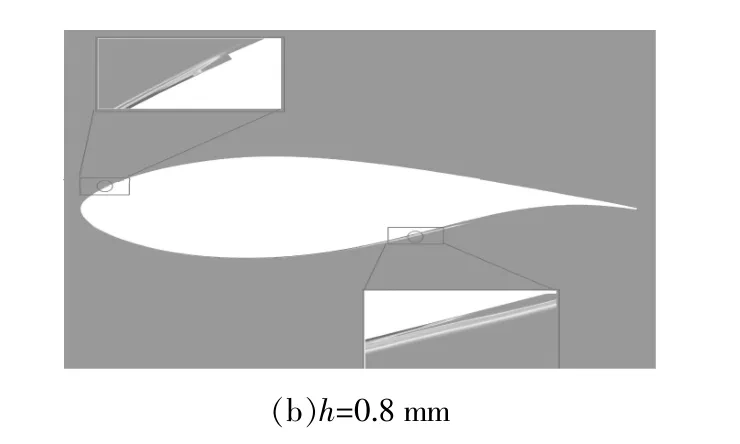
图11 不同凸台高度的DU91-W2-250翼型表面的流动转捩位置(α=9°)Fig.11 Flow transition location on smooth airfoil and rough airfoil surface(α=9°)
对于这两种翼型,在较大的h(2 mm)下,由于上表面凸台对来流气流的阻滞作用,粗糙翼型吸力面附近的气流总体动能减小,抵抗逆压梯度的能力减弱,从而在翼型吸力面尾缘出现大范围的流动分离。随着h的增加,分离区范围将逐渐变大,同时翼型的气动性能将进一步恶化。
通过显示全流场的间歇因子分布,得到了光滑翼型和粗糙翼型表面流动转捩位置的对比(图12)。由图12可知:在翼型上表面5%弦长位置处布置矩形凸台后,压力面转捩位置几乎不变,吸力面转捩位置大大提前;在较小的α下,光滑翼型吸力面转捩位置较靠后,粗糙翼型吸力面转捩位置位于矩形凸台上游,在翼型表面布置矩形凸台可以有效促进边界层内的流动由层流向湍流发生转变,从而减少最大CL。
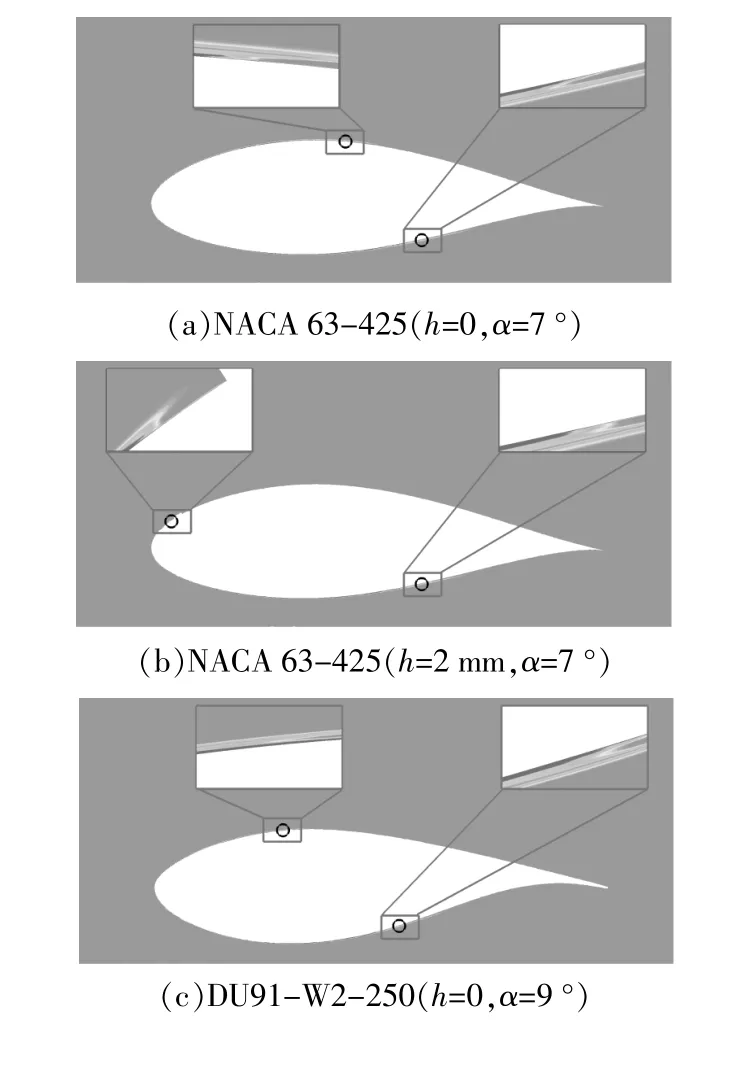
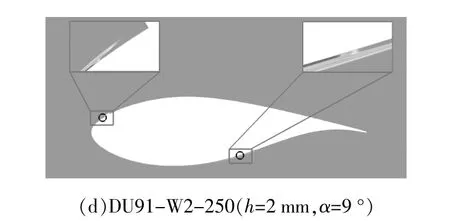
图12 光滑翼型和粗糙翼型表面的流动转捩位置Fig.12 Flow transition location on smooth airfoil and rough airfoil surface
2.2 不同凸台位置对翼型气动性能的影响
图13为不同凸台位置时,粗糙翼型的CL和CD变化曲线。其中,h固定为2 mm,凸台前端布置在翼型吸力面1%~30%弦长位置。
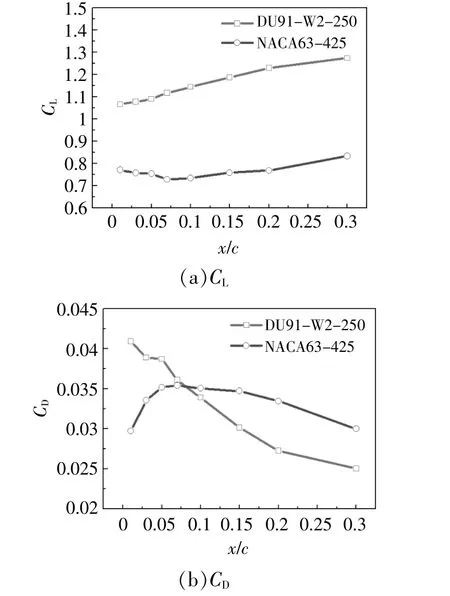
图13 粗糙翼型升、阻力系数随凸台位置的变化Fig.13 Rough airfoil lift and drag coefficient change with the position of the boss
由图13可知:对于DU91-W2-250粗糙翼型,随着凸台向尾缘移动,翼型的CL逐渐提升,CD逐渐降低,气动性能逐步接近原始翼型;当凸台放置在30%弦长位置处时,翼型的CL和CD与原始翼型几乎相等,表明此时表面粗糙度对翼型气动性能几乎没有影响;对于NACA63-425翼型,当凸台布置在7%弦长处时,翼型的升力最小,阻力最大,这表明该处为翼型吸力面粗糙度最为敏感的位置;即使凸台位置非常靠后,粗糙翼型的CL和CD仍然不能恢复到光滑工况。
3 结论
①在风力机翼型表面布置矩形凸台可以有效地模拟翼型表面的粗糙度效应,但凸台的高度与实际锯齿形粗糙带的高度存在一定差别。
②在较小的凸台高度下,NACA63-425翼型的气动性能对粗糙度变化较敏感,增加表面粗糙度会迅速恶化翼型的气动性能,而DU91-W2-250翼型具有相对较好的粗糙度不敏感特性。在较大的凸台高度下,两种翼型的气动性能均随前缘粗糙度的增加而降低。
③不同翼型的粗糙度敏感位置和范围并不一致。DU91-W2-250翼型粗糙度最为敏感位置发生在翼型的最前缘,而NACA63-425翼型粗糙度最为敏感位置发生在距翼型前缘7%弦长处。在一定的粗糙度高度下,当吸力面粗糙度位置较为靠后时,表面粗糙度对DU91-W2-250翼型气动性能的影响可以忽略,而对NACA63-425翼型仍然有较大的影响。
