卫星地面测角系统环境温度误差补偿方法

陈雅璐 李志慧 李强 杨凯

(上海卫星装备研究所,上海 200240)

随着一系列高分辨率遥感卫星发射成功,民用遥感卫星已进入“高分”时代,这意味着深空精确测量和地面微小物体定位能力的上升。精密星上载荷能到达的技术指标,主要依赖于硬件先进程度和安装角度标校[1-2],而单机安装角度和定位精度是可以在地面上利用高精度卫星地面测角技术进行全方面监测与控制的[3]。如果能在地面实现单机角度的精确测量[4-5],就能为单机装配调试提供最接近真实值的基准,保证地面安装精度,从而确保单机在轨道运行的实际工作能力。

当前国内卫星研制过程中,卫星装配部门主要是通过经纬仪或自准直仪联机建站测量的方法,保证地面安装精度[6]。通过在不同位置上使用多台仪器同时测量待测目标,记录在各仪器坐标系下待测目标的空间角度数据,辅以软件运算,获得待测目标在某一特定坐标系下的空间角度数据。随着卫星地面测角系统精度的大幅提高,其对环境因素的敏感程度也急剧上升,工作期间的设备发热现象和总装厂房空调的控温偏差会造成周围环境温度场变化,引起机械结构耦合热变形,导致测角误差随工作时长不断累积。环境温度变化造成的“测不准”现象已无法忽略,目前已对此开展了多项研究。文献[7]中分析了惯性测量系统在陆地使用、航空使用2种工况下的定位精度影响因素。文献[8]中采用高阶高斯-马尔可夫模型描述工程热力场对系统支撑结构变形的影响。文献[9]中采用倾角传感器评估支撑平台变形情况,通过插值法计算平台变形量对光电设备测角的影响,实现对支撑平台变形带来的最大142″测角误差的有效补偿。另外,光学仪器设计手册中指出:减小温度变化造成的支撑结构热变形、空气介质折射效应及光管本体变形,有利于减小反射像点在CCD 分化板上的坐标变化,有利于提高示值稳定性[10-11]。上述研究主要针对高精度测量系统结构变形的影响因素和作用机理,而如何补偿结构变形引起的测角误差缺乏深入探讨,国内在环境温度引起测角误差的补偿方法研究方面起步较晚,技术基础较为薄弱。

本文提出一种卫星AIT 过程中的环境温度引起测角误差补偿方法,通过构建电子水平仪转动物理模型,实时解算准直装置和基准镜装置在任意转角位置的角度误差,应用于卫星地面测角的角度传递模型修正,以提高卫星AIT 测角过程的系统测角精度和示值稳定性。

1 系统测量原理

卫星地面测角是指采用以被测目标安装面的法线方向来确定被测目标位置偏向的方法实现对壳体结构精度和星上仪器设备安装精度的测量,以检测卫星及其设备的安装角度,以期尽早发现卫星的总装问题或技术设计问题。卫星高精度自动测角系统采用光电自准直仪,在高精度2轴转台、双轴电子水平仪及数控定位机构的支撑下,形成一套全位置卫星自动测角系统。该系统通过联站测量、大地基准构建、环境误差补偿等技术完成被测目标的角度辨识与数据显示。

1.1 自准直仪测角法

自准直仪测角法可实现高精度、小角度测量,目前测量不确定度可达±0.01″,与测量范围相当的经纬仪相比,精度提升了一个数量级,其测角原理如图1所示。

图1 自准直测角原理示意Fig.1 Schematic diagram of auto-collimation angle measurement principle

光电自准直仪由光源、分划板、分光棱镜、物镜和CCD 阵列构成。分划板位于物镜的焦面上,光源发出的光照到分划板,通过分划板上狭缝的光线经物镜形成平行光出射;出射的平行光线经被测目标反射后返回并在CCD 阵列靶面上成像;通过电路处理可以给出发射光线在靶面上的准确位置。当准直光线与被测目标法线方向重合时,光线按原路返回,此时返回光线在光电探测器上所成的像的中心O标定为系统零位。设平面反射镜法线方向与准直光线的夹角为α,反射光线经准直物镜后与主光轴所夹角为2α,此时返回光线所成的像的中心O 与系统零位相差距离为ΔL,物镜焦距为f,根据几何光学的基本原理可得

当α 很小时,2α ≈tan(2α),代入式(2),可得

由此可见,通过对光电探测器靶面上的图像信号进行处理,精确计算出像点中心距离零位的偏移量,即可获得平面镜法线方向与准直光学系统主光轴的夹角。

1.2 联机建站工作模式

如图2所示,目前使用的卫星地面测角系统包括准直测量分系统、机械结构分系统和伺服控制分系统。准直测量分系统包括1台准直装置(2维精密转台上安装光电自准直仪、电子水平仪)和2台基准镜装置(2维精密转台上安装基准反射镜、电子水平仪)。其中:2 维精密转台实现自准直仪绕方位轴、俯仰轴的转动,便于自准直仪与基准镜、自准直仪与被测镜之间互瞄成像。机械结构分系统包括环形转台、竖直立架、基准镜装置、卫星停放台等。准直装置安装在竖直立架的水平平台上,环形转台与竖直立架是一体结构,环形转台可搭载准直装置绕卫星停放台中心进行转动运动,竖直立架进行竖直方向的直线运动,实现准直装置的全位置覆盖。伺服控制分系统包括伺服电机、位置和速度传感器、控制电路、算法软件等。

图2 测角系统组成Fig.2 Composition of angle measurement system

联机建站工作过程如图3所示。测量前,需要对测量场进行标定,获得准直装置和基准镜装置空间位置、角度等信息。测量过程中,系统获取到被测目标的指令信息,驱动机械框架子系统进行水平转动和竖直运动,等待准直装置中2维精密转台的俯仰、方位方向运动到位,静置后取值,获得被测目标相对于自准直仪的角度信息。下一步,系统获取到准直基准的信息,准直装置继续运动,到位瞄准基准镜后取值,获得基准镜相对于自准直仪的角度信息。所有待测目标测量完成后,通过坐标变换获得任意待测目标相对于指定的星上基准的矢量夹角信息。

图3 联机建站工作过程Fig.3 Working process of online site construction

2 环境温度误差

2.1 系统误差产生机理

根据联机建站工作模式,下面进行详细的误差要素分析。工作过程中读取的参数有:被测目标镜在自准直仪中的读数、基准镜在自准直仪中的读数、准直装置中2维精密转台转过的角度、基准镜装置中2维精密转台转过的角度、环形转台转角、竖直立架直线位移等。从参数来源来看,测角系统误差主要由准直测量分系统瞄准误差和机械结构分系统定位误差组成,如图4所示。准直测量分系统瞄准误差主要包括:仪器成像误差、准直目标时的光轴一致性误差和气流导致的光斑抖动偏差。机械结构分系统定位误差主要包括:2维精密转台制造时产生的几何误差、装配时产生的轴系误差、作为仪器搭载平台的机械结构热变形误差、受迫振动误差及变形误差导致的坐标变换误差。当环境温度变化时,作为搭载平台的机械结构产生热变形,固连其上的准直装置和基准镜装置的中心轴随之倾斜,瞄准采样过程中设备绕中心轴的转动轨迹也一同倾斜。当前采用的角度测量传递算法中往往忽略热变形的影响,认为各处设备转动轨迹与理想水平面重合,但设备实际转动轨迹平面与理想水平面之间存在一定的夹角,从而引入了环境温度误差。

图4 系统误差要素分析Fig.4 Analysis of systematic error elements

2.2 误差实测辨识

为获得环境温度误差的真实量级,以投入使用的卫星高精度自动测角系统为研究对象,将总装厂房温度从20℃调整到25℃,人为制造5℃的温升,监测4 h内该系统测量同一静止棱镜的水平方位角(Xatc方向)、竖直俯仰角(Yatc方向)的角度输出结果,观察输出结果与环境温度曲线。当温度从20℃上升至25℃时,Xatc方向与Yatc方向的输出数据见图5。

图5 输出结果-温度变化曲线Fig.5 Measured results of temperature variations

图5中数据的漂移部分,由环境温度变化引起的系统结构热变形误差与准直仪器自身温漂组成。随着长时间工作元件发热,透镜表面的半径、厚度、透镜间的空气间隔、光学材料及周围空气的折射率、组件的实际尺寸都会发生相应的变化,即产生内部光路变形,由于自准直仪方位和俯仰测角光路结构相同,内部光路变形造成的方位角与俯仰角温漂应该相同,但试验观察到的现象是Yatc方向漂移现象远超Xatc方向。可以认为,环境温度变化引起的系统结构热变形误差引起的误差远大于光电仪器自身温漂,分离出的环境温度误差约为9″。

3 环境温度误差补偿方法

根据环境温度误差产生原理,它是由瞄准采样过程中设备绕中心轴的转动轨迹与理想水平面不重合造成的,因此应设法获得转动轨迹平面与理想水平面之间的实时偏角,从而对环境温度误差进行补偿。本文设计的补偿方法是:在卫星地面测角系统准直装置和基准镜装置的精密2维转台内嵌入安装双轴电子水平仪,根据水平仪转动特性周期性规律,选取0°,90°,180°,270°作为特征位置,读取4点水平度并建立方程组,求解实际轨迹平面与理想水平面的最大夹角,实时解算任意位置的实时偏角并建立补偿矩阵,最后代入系统角度传递模型进行修正,消除此偏角引入的测角误差,实现环境温度误差的补偿,具体流程如图6所示。

图6 环境温度误差补偿方法流程Fig.6 Flow of environment temperature error compensating method

3.1 水平仪转动特性

如图7所示,电子水平仪可同时测量平面内正交的2个方向的水平倾角,安装在准直设备和基准镜设备上后,随着设备的转动作同步运动,转动周期内的电子水平仪读数不断变化。在水平仪转动1周过程中,设备绕中心轴的转动轨迹与理想水平面之间的实时偏角呈现周期性规律。根据几何关系,以转动轨迹平面与水平面交线为Y 轴,分别建立转动轨迹平面与水平面坐标系,其中,XEOY 面为理想水平面,XROY 面为转动轨迹平面,如图8所示。

图7 双轴电子水平仪Fig.7 Dual-axis electronic level instrument

图8 两平面的几何关系Fig.8 Geometric relations between two planes

设转动轨迹平面与理想水平面的夹角达到最大值θmax时对应的转台单位矢量为OA′,OA′在水平面内的投影是OA,将OA′转动角度φ至OB′,OB′在水平面内的投影是OB,OB 与OB′的夹角为θ。过点B作XE轴的垂线BC,过点B′作XR轴的垂线B′C′。瞬时夹角θ与最大值θmax、转角ψ 的关系可表示为

因此,只要确定转动轨迹平面和水平面的夹角最大值θmax,以及相对最大偏角位置的转角ψ,就可以获得任意位置的偏角θ。但是,最大偏角θmax对应的位置是未知的,可通过水平仪在2个已知位置的转角和读数,求解逆函数得出。

设水平仪方位角分别转动0°,90°,180°,270°时,XR轴方向读数分别为α1,α2,α3,α4,XR轴方向夹角最大值为αmax,Y 轴方向读数分别为β1,β2,β3,β4,Y 轴方向夹角最大值为βmax,水平仪安装面与水平面的XR轴方向、Y 轴方向夹角分别为,δY,可列出方程组为

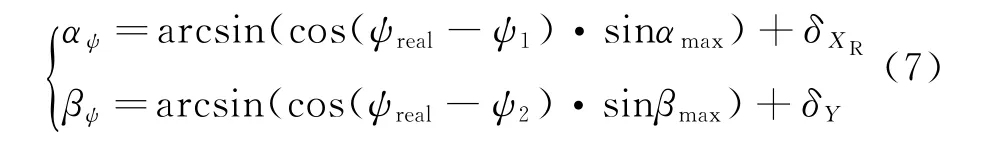
3.2 角度传递模型修正

任意位置偏角表征的是当前位置转动轨迹平面与理想水平面之间的夹角,应在准直装置和基准镜装置每次转动后加入偏角补偿,获得真实角度。因此,在卫星地面测角系统的角度传递模型中找到所有设备转动动作,在其后代入补偿矩阵,即可补偿环境温度变化引起的测角误差,修正后的角度传递模型如图9所示。图9中:光电自准直仪固有坐标系为像面坐标系P,准直装置中的2维精密转台处于零位时的坐标系为准直坐标系A0,当准直装置瞄准1号基准镜装置时,准直装置、1号基准镜装置中的2维精密转台方位、俯仰均发生转动,记当前位置准直装置的坐标系为准直坐标系A1,1号基准镜装置的坐标系为基准镜1坐标系M1,当1号基准镜装置中的2维精密转台回零时记为基准镜1坐标系M0。同理,当准直装置瞄准2号基准镜装置时,记当前位置2号基准镜装置的坐标系为基准镜2坐标系N1,回零时记为基准镜2 坐标系N0,记大地坐标系为G。假设待测目标棱镜法线矢量在像面坐标系P中的坐标为νP,待测目标棱镜法线矢量在大地坐标系G中的坐标为νG,从像面坐标系P转换到准直坐标系A0的变换矩阵为,从准直坐标系A0转换到准直坐标系A1 的变换矩阵为,从准直坐标系A1转换到基准镜1坐标系M1的变换矩阵为,从基准镜1坐标系M1转换到基准镜1坐标系M0的变换矩阵为,从基准镜1坐标系M0转换到大地坐标系G 的变换矩阵为。

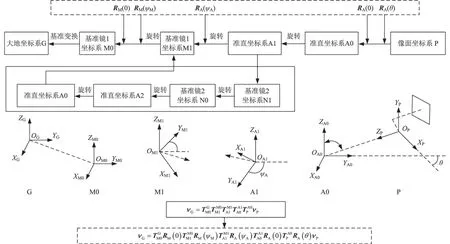
图9 修正后的角度传递模型Fig.9 Angle transformation model after correction

假设准直装置或基准镜装置中的2维精密转台转动角度ψ 到达预设位置,对应的温度误差补偿矩阵记为Ri(ψ),其中,当前坐标系为准直坐标系A0或A1时,下标i写为A,当前坐标系为准直坐标系M0或M1时,下标i写为M。RA(0)表示准直装置在未发生转动时的补偿矩阵;RA(θ)表示准直装置在转动角度θ 后瞄准被测目标的补偿矩阵;RA(ψA)表示准直装置在转动角度ψA 后瞄准1号 基准镜的补偿矩阵;RM(ψM)表示1号基准镜装置转动角度ψM后被准直装置瞄准的补偿矩阵;RM(0)表示1号基准镜装置回零的补偿矩阵。

4 标定试验验证

为了验证基于双轴电子水平仪转动特性进行的角度传递模型修正的有效性,在卫星装配厂房内进行标定试验验证。采用的验证方法是:以23面体棱镜工作面夹角为被测目标,保持周围安静,采用空调系统控温方式改变环境温度,分别采用常规算法角度传递模型和引入补偿方法处理的新模型进行测量,通过处理前后测量误差的对比进行验证。

4.1 试验系统

如图10所示,试验系统包含热电偶传感器、零度控温器、数据采集器、测温软件、23 面金属棱体(静止被测目标)、基准镜、自准直仪等设备。图11为试验系统实物图。

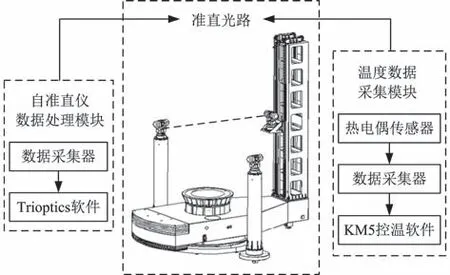
图10 试验系统结构示意Fig.10 Experimental system structure diagram

图11 试验系统实物Fig.11 Experimental system

4.2 试验流程

试验按照以下步骤进行。

(1)将热电偶传感器粘贴于竖直立架高位、中位、低位3处,光路靠近自准直仪处、中间部分、基准镜处。

(2)检测环境温度(测量值约为20℃),通过空调将厂房温度从20℃升高到25℃,净化风关闭,打开设备预热。

(3)在空调开启的2 h内,采用常规算法角度传递模型,操作卫星高精度自动测角系统,使自准直仪瞄准23面棱体任一个工作面及其相邻工作面,测量2个工作面夹角,计算并记录温度和测量结果。

(4)重复(3)中操作17次。

(5)通过空调将厂房温度从25℃降回到20℃,净化风关闭,温度均匀后重新升温至25℃。引入环境温度误差补偿矩阵修正角度传递模型,操作卫星高精度自动测角系统,使自准直仪瞄准23面体棱镜任一工作面及其相邻工作面,测量两个工作面夹角,计算并记录温度和测量结果。

(6)重复(5)操作17次。

(7)将测量结果与棱镜相邻工作面夹角的标定值比较,并计算测量误差,记录在表格中。

4.3 试验结果及分析

环境温度误差补偿方法处理前后的2组试验结果见表1。为了直观反映试验结果,绘制如图12所示的散点图。

表1 测角误差Table 1 Angle measurement errors

图12 测角误差对比Fig.12 Comparison of angle measurement errors

由试验数据可知:温度变化造成的机械结构耦合热变形现象会引起角度测量值不断向误差增大的方向偏移,对测角精度和重复精度均产生不利影响。对比环境温度误差补偿方法处理前后的系统测角误差可知:在环境温度产生5℃温升时,常规方法下的测角误差从2.5″增加到9.6″,增幅约7″;应用温度补偿方法后,测角误差从2.5″增加到3.0″,增幅仅0.5″。这表明:基于双轴电子水平仪转动特性的温度补偿方法是有效的,该方法将卫星高精度测角系统的综合测角精度从接近10″提高至3″,重复测量精度提高至1.1″,未来可应用于卫星装配测试领域,实现环境温度误差的有效补偿和测试结果的稳定输出,为超高精度的卫星AIT 测角过程提供有力支撑。

5 结束语

针对环境温度扰动导致的测角示值波动过大、测角精度无法进一步提高、微小角度甚至无法测量的问题,本文提出一种卫星AIT 过程中的环境温度误差补偿方法,通过对电子水平仪转动特性的分析,获得任意转角位置误差解算方法,可应用于新型高精度卫星地面测角系统,并依据相关标准完成有效性验证。验证结果表明:该方法能将卫星地面测角精度提高至3″,重复精度提高至1.1″,未来可应用于卫星装配测试,实现高精度、高稳定、自动化的卫星地面测试,为超高分辨率遥感卫星的研制打下基础。