星敏感器支架多学科多目标优化设计方法

裴彦伟 谭陆洋 谷松,2 张雷,2 侯广冰

(1 长光卫星技术有限公司,长春 130033)(2 中国科学院长春光学精密机械与物理研究所,长春 130031)(3 中国科学院东北地理与农业生态研究所,长春 130033)

星敏感器作为航天器姿态测量的高精度器件,其测量精度直接决定了卫星的姿态确定精度[1-2]。由于星敏感器指向角度要求,需通过支架作为转接安装在有效载荷框架上。卫星在发射过程中,受到火箭产生的振动、冲击等恶劣环境,这些环境激励通过卫星结构经支架作用在星敏感器上,影响星敏感器工作性能和可靠性。与此同时,随着光学卫星的分辨率的不断提高及航天技术的快速发展,对卫星的指向精度、姿态稳定度和结构轻量化的要求越来越高[3]。卫星实际在轨工作处于反复交变的恶劣环境,而高精度星敏感器又对工作环境极为敏感,微小的环境变化都会产生较大的指向精度误差,提供星敏感器安装平台的支架,其热稳定性直接影响星敏感器定姿精度。因此,星敏感器支架结构质量、刚度、动响应特性和热稳定性等因素直接关系到星敏感器工作的可靠性和指向精度。这涉及到多个领域和多个目标,需进行多学科、多目标、多系统的协同优化设计。

星敏感器因其具有空间适应性强、精度高等优点,被众多航天器所采用[4-5]。因此,国内外对星敏感器自身精度、系统姿态确定算法优化研究较为深入,但对其安装支架结构设计研究较少且不够全面,并且传统的方法大多数都是基于单学科单目标,拓扑优化获取的结构形式无法保证在轻量化后,同时满足高比刚度、高可靠和高热稳定性的多领域指标要求,而随着光学卫星分辨率的不断提高,热稳定性对星敏感器指向精度影响作用越发凸显。文献[6]将拓扑优化方法和增材制造技术结合设计了一种高比刚度星敏感器支架,文献[7]设计了高刚度的星敏感器支架,文献[8]设计了复杂空间角双星敏感器组合支架,具有质量轻、易于制造等优点,文献[9]采用C-C石墨材料进行星敏感器热控制设计,满足星敏感器组合体在轨的严格温度控制要求,降低了星敏感器支架热变形,文献[10]采用碳纤维、碳化硅复合材料设计了一种高热稳定性的多星敏感器组合支架,并进行了热试验验证。以上学者从质量、刚度、热变形等方面对星敏感器支架进行设计,但没有在设计之初考虑多学科耦合问题,都是在单学科或单学科多目标范围开展研究。目前,星敏感器支架轻量化设计过程中,没有形成一套基于多学科多目标的优化求解设计方法。

本文从高分辨率光学卫星对角秒级星敏感器支架研制需求出发,提出一种面向高比刚度、高指向精度星敏感器支架的多学科多目标优化设计方法。建立静态柔度和动态刚度为多目标的拓扑优化数学模型,考虑卫星发射阶段和在轨工作的静力学、动力学和热学等领域,进行多学科协同优化,设计出新型圆筒式星敏感器支架,大幅降低结构质量,同时提高了星敏感器发射阶段抗力学扰动的能力和在轨工作的指向精度。经过力学和热学多学科仿真分析,结合地面振动和热真空试验,验证了此方法在高精度部件结构设计方面的可行性,同时表明圆筒式支架具有较高的比刚度和热稳定性,满足高分辨率光学卫星对其星敏感器高指向精度的要求。

1 多学科多目标优化

1.1 多目标拓扑优化数学模型

拓扑优化在不同的应用领域取得巨大成功,但大多数研究都集中在单一学科,而航天器结构经历复杂的力/热环境,多学科多目标拓扑优化设计显得尤为重要[11-13]。本文考虑星敏感器组件在热、力载荷下的多目标拓扑优化问题,保证多个目标为最优解,基于折衷规划法对多个优化目标进行加权,将多目标优化问题等价为单目标优化问题,获取合理数值优化结果。依据SIMP密度-刚度函数插值模型,建立多种静态拓扑优化工况,静态工况主要包括卫星发射阶段和在轨工的力/热载荷。寻求刚度最大化问题需要转换为柔度最小问题,而柔度则利用应变能来定义,获取以柔度C(ρ)最小为目标函数,将体积作为约束条件,目标函数如下

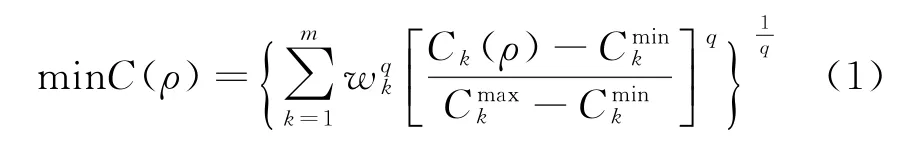
式中:m 为载荷工况总数;wk为第k个工况的权值;q 为惩罚因子,q≥2;Ck(ρ)为第k 个工况的柔度目标函数;分别为第k 个工况柔度目标函数的最大值和最小值。

采用平均频率方法来避免优化过程目标函数出现振荡问题,平均频率公式来定义固有频率拓扑优化的目标函数

式中:Λ(ρ)为平均频率;εn为第n 阶特征频率;ε0、s为目标函数调整参数;wn为第n 阶频率的权重系数;N 为需要优化的低阶频率的阶次。

综合以上分析,考虑发射阶段和在轨工作动静力学、热学等多工况的多目标拓扑优化函数为

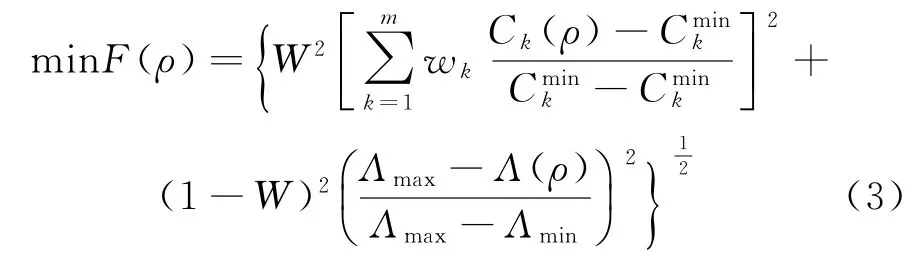
式中:F(ρ)为综合目标函数;W 为柔度目标函数的权重;Λmin、Λmax分别为频率目标函数的最小值和最大值。

1.2 多目标拓扑优化参数获取

本文采用层次分析法并结合实际工程经验确定子目标权重,相对结构刚度而言,高分辨光学卫星对热稳定性要求更高。因此,静态柔度拓扑优化中过载和热变形两种静态工况,对结构热变形更为关注,分别取0.3和0.7;动态频率拓扑优化中前三阶固有频率,分别取0.5、0.3和0.2。进行支架优化前后的静力分析和模态分析,获取支架的柔度最大值和最小值、平均频率最大值和最小值。在多目标综合目标函数中,取柔度权值0.55,频率权值0.45,分析完成后,获取的各个工况下参数如表1所示。

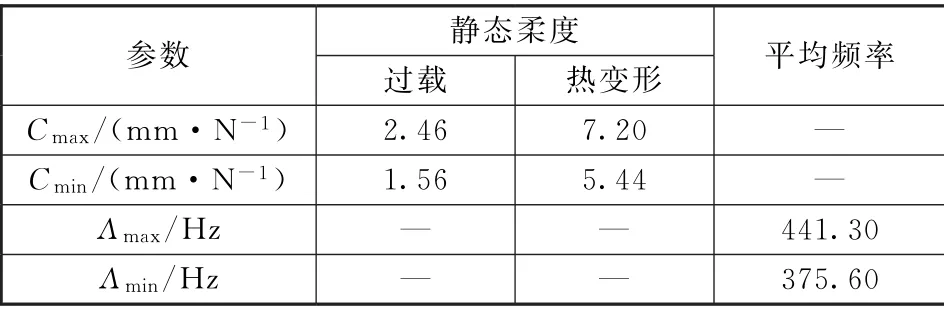
表1 各工况下参数结果Table 1 Parameter results under various working conditions

选取通用型号的星敏感器作为本方法优化对象,质量为1.15 kg,优化前支架质量为0.512 kg,星敏感器简化为质量点,采用刚性杆单元(rbe2)连接,优化前有限元模型如图1所示。

1.3 星敏感器支架多学科多目标拓扑优化

卫星从发射到在轨受到复杂的力学与空间环境影响[16],涉及力学、热学多个学科领域。星敏感器支架的热载荷主要为在轨工作的高低温环境,只存在温度载荷时,其有限元离散准静态热变形方程为

式中:R 为结构温度节点载荷列阵;u 为结构节点的位移列阵;K 为结构整体刚度矩阵。

考虑热变形引起星敏感器安装型面精度的影响,设星敏安装面上各节点原始坐标为xJ,yJ,zJ,热变形后的坐标为x′J,y′J,z′J,型面变形精度均方根值(erms)值为

引入星敏感器安装型面精度,同时结合体积分数、安装点应力和制造工艺约束,多学科多目标拓扑优化数学模型可描述为

式中:x 为设计变量,xe为单元设计变量,xmin、xmax分别为单元设计变量最小和最大极限值;Δr 为型面精度约束值;σ、[σ]分别为设备安装点应力和约束值;α、[α]分别为优化体积比和约束值。

为了保证支架具有低质量、高刚度、低动态响应和高热稳定性等多学科设计要求,采用以上方法进行优化设计。经过80步迭代运算,目标函数迭代曲线如图2所示,获取最终优化模型如图3所示。

图2 多学科目标函数迭代曲线Fig.2 Iterative curve of multidisciplinary objective function

图3 拓扑优化结果Fig.3 Result of topology optimization

优化后,星敏感器支架质量降低了47.5%,4个安装点由热变形引起的位移降低15.3%,基频为412.7 Hz。结合加工工艺和星敏感器安装要求,对拓扑优化结果进行适当调整,支架最终质量0.269 kg,加工后的结构形式如图4所示。

图4 加工后的星敏感器支架Fig.4 Star sensor bracelet after processing

2 热变形及振动响应特性分析

2.1 星敏感器支架热变形分析

整星在轨工作时,支架的温度变化引起的热变形是影响星敏感器定姿误差的主要因素,对星敏感器支架热变形分析至关重要。卫星的温度边界条件设置是根据卫星所处的轨道环境和内热源分布热仿真获取,然后将温度数据映射到力学有限元分析软件中,进行整星热稳定性分析,获取节点热应变和热应力数据。根据热分析结果可知,整星处于高温工况时,星敏感器支架的温度变化最大,因此选择高温工况作为热变形分析极端工况,整星在轨极端工况的主要结构件温度分布如表2所示。

表2 主要结构件温度分布Table 2 Temperature distribution of main structural parts ℃

获取星敏感器相对于光学载荷指向角度,提取星敏感器安装面的节点位移拟合出一个曲面求得其法线。同样地,将光学相机主镜镜面的节点位移拟合出一个曲面,并求得其法线。这两条法线的夹角即指向角度,它们热变形前后的夹角变化大小即为指向精度。

设星敏安装面上各节点原始坐标和热变形后的坐标矩阵表示为

基于最小二乘法平面拟合和空间平面方程为

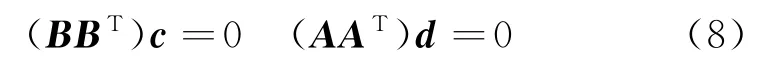
式中:c 为热变形后星敏安装面拟合曲面的法向向量;d 为原始面的法向向量。

同样可得到光学载荷相机主镜面热变形后拟合曲面的法向向量为e 和原始面的法向向量为f。

向量夹角为

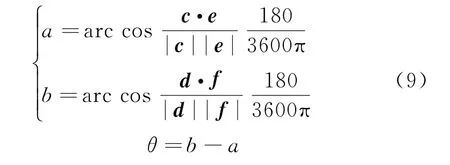
式中:a 为初始状态星敏感器安装面和光学载荷相机主镜面法向指向夹角;b 为热变形时两个法向指向夹角;θ 为星敏感器相对光学载荷相机的指向精度,单位为角秒(″)。

基于有限元方法对优化前后的圆筒式支架进行热变形分析。提取星敏感器安装面节点位移数据,对其进行拟合并获取安装面法线,获取星敏感器自身以及与光学相机法线相对基准轴的变化,进而计算获取其法线之间的夹角变化,如表3所示(表中Δα、Δβ、Δγ 分别为星敏感器安装面法线(即星敏感器光轴)的方向角的变化量)。

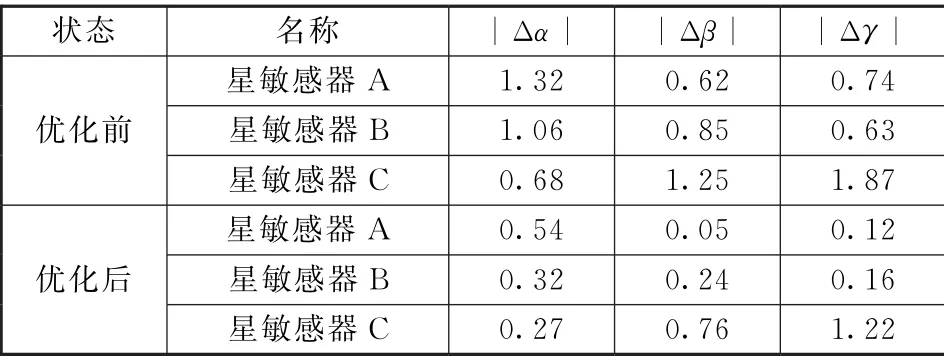
表3 极端工况下各星敏感器安装面法线方向角变化值Table 3 Change value of normal direction angle of star sensor mounting surface under extreme conditions (″)

从表3中可以看出,优化后的圆筒式支架相对优化前热变形明显降低,优化后的支架热变形最大1.22″,圆筒式支架在热载荷作用下变形分布均匀,具有较高的抗热扰动能力,为敏感器件提供稳定的安装平台。

光学相机基板温差为(2±0.1)℃,星敏感器组件温差为(3±0.2)℃,进行整星的热变形分析并计算获取星敏感器指向精度如表4所示。

表4 星敏感器指向精度Table 4 Pointing accuracy of star sensor (″)

从表中可以看出,优化后的圆筒式支架相对优化前指向精度大幅提高,优化后的支架结构的指向精度优于3″,满足微小卫星对比刚度和指向精度等高性能指标的要求。

2.2 星敏感器支架振动响应特性分析

从结合实际工程应用,对有限元模型进行必要的假设和简化。将相机基板支腿连接面作为加速度载荷的加载面,计算工况:频率范围为0～100 Hz,分别单独施加X、Y 向量级为2gn,Z 向量级为1.5gn,选取的位置及加速度响应结果如表5所示。

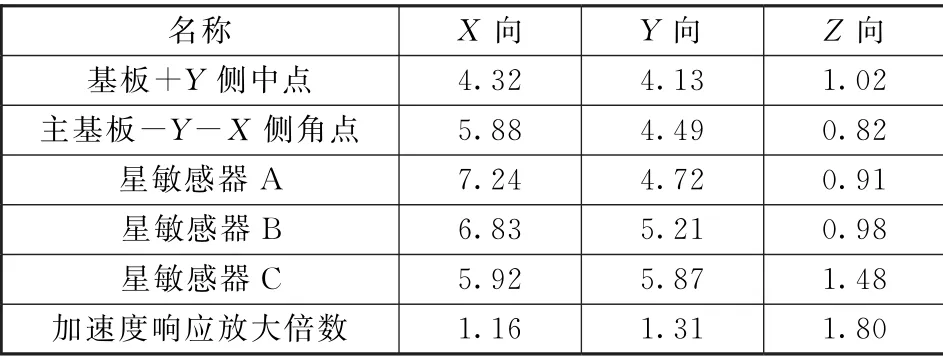
表5 加速度响应结果Table 5 Acceleration response results g n

通过分析可知,支架加速度响应放大倍数不超过2倍,具有高刚度、低动态响应系数。综合以上热变形和结构力学仿真分析,采用多学科多目标优化方法,获取的拓扑结构具有优异的结构/热稳定性,是传统单学科、单目标方法很难达到的。同时,圆筒式结构具有优异的抗力/热扰动的特性,远优于传统框架式结构。

3 试验验证

3.1 热变形试验

为了验证多学科多目标优化设计方法可行性和热变形分析的准确性,整星进行热真空试验。由于受地面真空热试验设备的限制,无法在真空状态下使用经纬仪标定获取试验数据,而是通过采用应变片获取真空环境下星敏感器支架的热变形数据,与有限元分析获取应变数据进行对比,间接验证其热变形分析的准确性,应变片分布位置如图5所示。

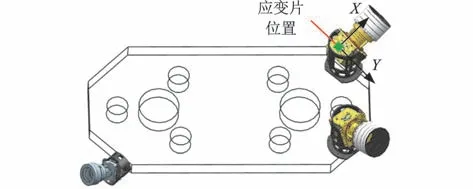
图5 应变片位置Fig.5 Position of strain gauge

整星在真空热试验设备时间约为2天,获取支架从低温到高温模拟环境的应变数据。对试验数据进行多项式拟合,得到横坐标为时间,纵坐标为应变的曲线,获取星敏感器支架X、Y 向应变曲线如图6所示。从曲线可以看出,经高低温环境,支架X 向最大应变为9.84με,Y 向最大应变为11.23με,通过有限元分析热分析,获取支架应变数据如表6所示。

表6 支架应变结果Table 6 Strain results of bracket

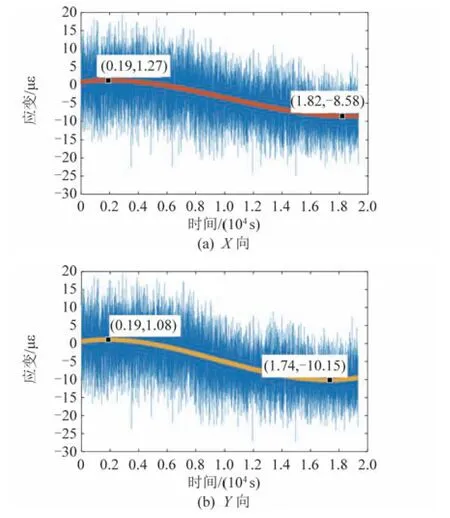
图6 热应变曲线Fig.6 Curve of thermal strain

考虑温度控制、传感器读取数据等试验误差,仿真数据与试验数据的偏差在合理范围内,从对比结果可以间接验证了支架的热稳定性分析的准确性,印证基于结构/热的多学科多目标拓扑优化方法的可行性,同时,表明圆筒式支架具有较优的热稳定性。

3.2 振动响应特性试验

正弦扫描和正弦振动响应特性试验主要是获取星敏感器支架加速度响应等参数,以及星敏感器组件一阶固有频率,验证支架力学性能是否满足技术指标要求,振动试验如图7所示。

图7 振动响应特性试验Fig.7 Vibration response characteristic test

星敏感器A 和B位置相近,只在星敏感器A 安装点附近放置传感器,对应通道如表7所示。

表7 相应位置传感器通道号Table 7 Corresponding position sensor channel number

对星敏感器组件进行正弦扫描试验获取支架固有频率,相机组合体进行正弦振动试验获取动态响应数值,试验结果如图8所示。

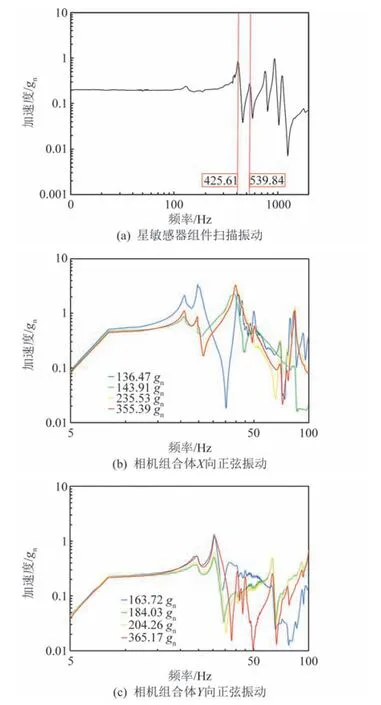
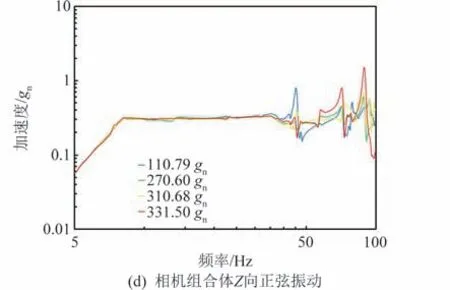
图8 振动响应特性试验数据Fig.8 Data of vibration response characteristic test

从振动试验结果中数据可以看出,星敏感器组件一阶固有频率为425.6 Hz,光学相机主承力框架和3个星敏感器的振动响应接近一致,仿真数据相与试验数据趋势一致,二者基本吻合,有限元法进行动力学计算结果准确可信,表明支架经过多学科多目标优化后,获取的高比刚度的结构形式具有较低动态响应系数和较高的结构稳定性,能够满足卫星发射阶段力学环境。

4 结束语

本文从高分辨率光学卫星对角秒级星敏感器支架的研制需求出发,基于结构/热一体化思想,提出一种多学科多目标的拓扑优化设计方法。建立了多学科多目标优化数学模型,并采用此方法设计了一种新型圆筒式星敏感器支架,结构质量0.269 kg,轻量化率47.5%,指向精度2.71″。对优化支架进行了振动响应试验和热稳定性试验,验证了多学科多目标拓扑优化方法在高精度敏感器件结构设计上的可行性。此优化方法能够解决传统优化方法无法考虑实际应用中多个目标和多领域的协同优化问题,拓宽了考虑设计因素的领域范围,能够在满足约束条件下,获取多个性能指标的最优解,适应航天技术的飞速发展,对于提升高分辨率光学卫星性能指标的具有重要意义。此外,本文的设计方法和结构目前已在某卫星得到实际应用,优化方法对于其他指向精度和姿态稳定性要求高的卫星结构设计具有一定借鉴意义,同时结构形式可为相关设计提供新的设计灵感。