应用星载AIS双天线的舰船快速定位方法

李洋 张杨 朱浩平 丁振宇 王韶波 王丽丽 刘航 梅名宣

(1 航天东方红卫星有限公司,北京 100094)(2 山东航天电子技术研究所,山东烟台 264003)

自动识别系统(AIS)是一种基于甚高频的舰船自主报告系统,舰船自主发送身份信息、位置、速度、航向和其他信息,用于避免舰船碰撞和全球舰船监管。国际海事组织于2002年强制要求300 t以上的国际航线舰船和500 t以上的国内航线舰船安装AIS,目前该系统已在全球范围内得到广泛应用。星载AIS接收可视海域内的AIS信号,为全天候、大范围的舰船监管提供数据服务[1-4]。当舰船全球导航卫星系统(GNSS)失灵、受扰或舰船需要救援时,通过星载AIS可实现定位解算。

目前,国内外已对应用星载AIS的舰船定位方法进行了研究。文献[5]中提出利用星载AIS接收信号的频偏确定发送信号位置。文献[6-7]中提出了测频时差联合定位模型。上述文献中的定位方法均基于单星单天线AIS接收,定位解算需要至少接收同一舰船的2次信号,且基于发送信号间隔相等的假设。然而,实际中舰船发送信号间隔并非保持不变。对于伪装的军事舰船或从事非法活动的舰船,存在仅发送1次信号的现象。对于仅发送1次信号的接收定位,文献[8-11]中研究了三星定位和双星频差时差定位方法。相对于单星系统,编队卫星系统增加了构型维持和星间链路等技术的复杂性。在舰船定位解算方面,国内外文献中通常先求出接收信号天线到舰船的距离,在此基础上再解出舰船的位置。文献[5]中采用在不同位置接收同一舰船AIS信号的2次多普勒频率方法求解天线到舰船的距离,该方法中求解天线到舰船距离的4次方程,需要复杂验根才能得出。文献[6-7]中采用卡尔曼滤波算法直接求解舰船位置,但该算法的初值采用网格搜索的方法给出,网格搜索方法和卡尔曼滤波算法的计算量较大,解算速度较慢。

针对上述问题,本文提出单星AIS双天线接收的舰船快速定位方法。首先,通过舰船位置与星载AIS接收信号多普勒频率,以及双天线接收信号时差关系,得出双天线到舰船距离的线性方程组。然后,在此基础上,建立舰船定位解算模型。最后,通过理论推导和仿真计算给出卫星位置速度精度、星载AIS接收频率精度和时差精度、天线相位中心精度、双天线距离及安装位置对定位精度的影响。本文方法能满足仅接收1次信号实现舰船定位的需求,且方法简便、解算快速,适用于星上实时快速解算和自主判断舰船位置。

1 舰船快速定位方法

本文提出的应用星载AIS双天线接收的定位方法,首先将双天线的坐标由卫星本体坐标系转换到地固坐标系,然后通过测量得到AIS信号的多普勒频率及双天线接收信号的时差,在地固坐标系下得出双天线分别到舰船位置的线性方程组。本文方法实现过程如图1所示,具体步骤如下。

图1 舰船快速定位方法实现过程Fig.1 Method process for fast ship positioning

(1)求解舰船的定位问题,需要已知卫星双天线在地固坐标系的坐标。卫星发射前,可以测量天线在本体坐标系的坐标;发射入轨后,结合卫星轨道姿态参数经坐标转换,求出天线在地固坐标系中的坐标。

(2)利用接收信号多普勒频率与天线和舰船相对速度的关系,以及天线到舰船距离与两者相对速度的关系,得出星载AIS接收多普勒频率与天线到舰船距离的关系,联合双天线接收时差与双天线到舰船距离的关系,进一步得出双天线到舰船距离的线性方程组,求解出双天线分别到舰船的距离。

(3)联合步骤(1)和步骤(2)的结论,建立舰船定位方程,解出舰船位置。

1.1 天线位置的坐标转换

1.1.1 坐标系定义及转换关系

卫星发射前,已知天线在卫星本体坐标系的坐标;卫星发射入轨后,通过地固坐标系与卫星本体坐标系之间的转换关系,将天线在本体坐标系中的坐标转换到地固坐标系中。在坐标转换过程中涉及到的坐标系有地固坐标系、地心轨道坐标系、质心轨道坐标系和卫星本体坐标系,各个坐标系的示意见图2。坐标系的具体说明如下。

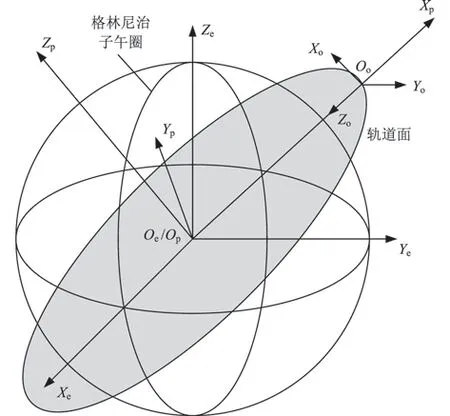
图2 坐标系示意Fig.2 Schematic diagram of coordinate system

(1)地固坐标系Oe－XeYeZe,原点Oe在地球中心,Xe轴在地球赤道平面内指向格林尼治子午线,Ze轴与地球自转轴重合,指向北极,Ye轴和Xe轴、Ze轴成右手正交坐标系。

(2)地心轨道坐标系Op－XpYpZp,原点Op在地球中心,Xp轴指向卫星,Zp轴与卫星轨道面的法线重合,Yp轴和Xp轴、Zp轴成右手正交坐标系。

(3)质心轨道坐标系Oo－XoYoZo,原点Oo在卫星质心,Xo轴指向卫星飞行方向,Zo轴指向地球中心,Yo轴和Xo轴、Zo轴成右手正交坐标系。

(4)卫星本体坐标系Ob－XbYbZb。卫星在没有自旋和姿态偏差时,卫星本体坐标系Ob－XbYbZb的各轴与质心轨道坐标系Oo－XoYoZo的各轴重合。

设AIS天线在上述4个坐标系中的坐标分别为ae＝ [xeyeze]T,ap＝ [xpypzp]T,ao＝[xoyozo]T,ab＝[xbybzb]T。

地固坐标系Oe－XeYeZe到地心轨道坐标系Op－XpYpZp的转换关系为[12-13]

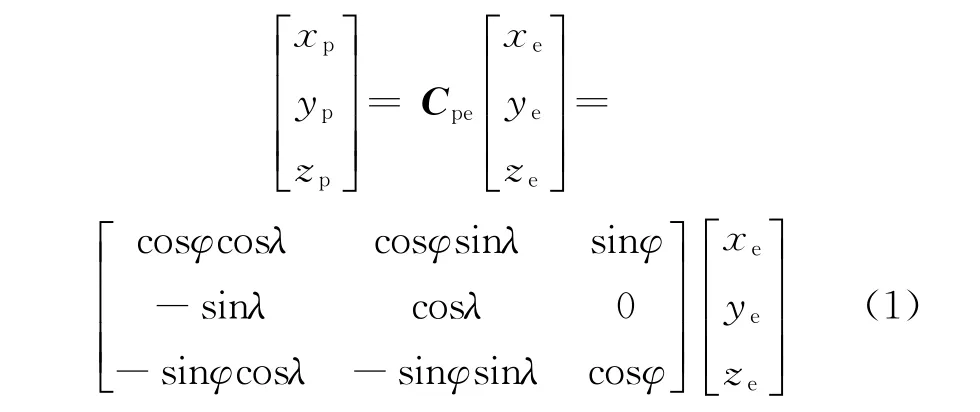
式中:Cpe为地固坐标系到地心轨道坐标系的转换矩阵;λ 为卫星经度;φ 为卫星纬度。

地心轨道坐标系Op－XpYpZp到质心轨道坐标系Oo－XoYoZo的转换关系为

式中:Cop为地心轨道坐标系到质心轨道坐标系的转换矩阵;sp＝[xsat_pysat_pzsat_p]T为卫星质心在地心轨道坐标系中的坐标。

在本文后续计算中,认为卫星没有自旋或姿态偏差,因此,质心轨道坐标系Oo－XoYoZo到卫星本体坐标系Ob－XbYbZb的转换关系为

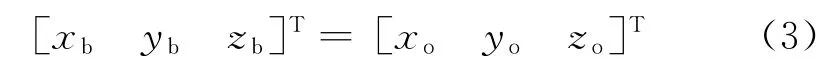
1.1.2 AIS天线在地固坐标系中的坐标

AIS天线在地固坐标系中的坐标转换到地心轨道坐标系的坐标时,ap＝Cpeae;转换到质心轨道坐标系时,ao＝Cop(ap－sp);转换到卫星本体坐标系时,ab＝ao。经上述坐标转换,有

由此得出,AIS天线在地固坐标系中的坐标为

式中:se为卫星质心在地固坐标系下的坐标。

式(5)为已知AIS天线在卫星本体坐标系下的坐标ab,计算天线在地固坐标系下坐标ae的公式。

1.2 双天线分别到舰船距离的解算

星载AIS双天线随着卫星运动,接收到的AIS信号会产生频率偏移,即多普勒频率。多普勒频率的计算公式为

式中:fc为AIS信号的载波频率,一般为162 MHz;光速c＝3×108m/s;vd为星载AIS天线与信号发射舰船在信号传播方向上的相对运动速率,可表示为式(7)。

式中:天线在地固坐标系的速度矢量可表示为v＝[vXvYvZ]T;θ 为天线速度矢量与信号传播方向之间的夹角。

信号发射端和接收端的距离减小,多普勒频率为正;距离增大,多普勒频率为负。信号传播方向为海面舰船指向星载AIS天线,此方向上相对运动速度为正时引起发射端和接收端距离增大,多普勒频率为负。

在地固坐标系中,信号传播方向矢量表示为r＝ae－u,舰船位置矢量可表示为u＝[x y z]T。由此,信号传播方向与天线速度矢量的夹角θ 可表示为

将式(8)代入式(7),结果为

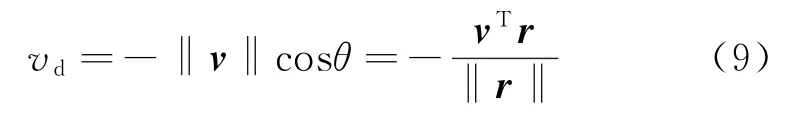
因此,得出星载AIS天线接收到的信号多普勒频率为

设星载AIS双天线在地固坐标系中的坐标分别为a1e＝[x1ey1ez1e]T和a2e＝[x2ey2ez2e]T,接收到同一AIS 信号的多普勒频率分别为f1和f2,速度矢量分别表示为v1和v2。双天线在同一卫星上,速度矢量等于卫星速度矢量,可表示为v1＝v2＝v＝[vXyYzZ]T。根据式(10)可得

双天线到舰船位置的距离分别为r1＝a1e－u和r2＝a2e－u,双天线接收到同一AIS信号的时间差t通过测量得到,可表示为

联合式(11)和式(12),得出解算舰船位置的方程组为

式(13)可表示为

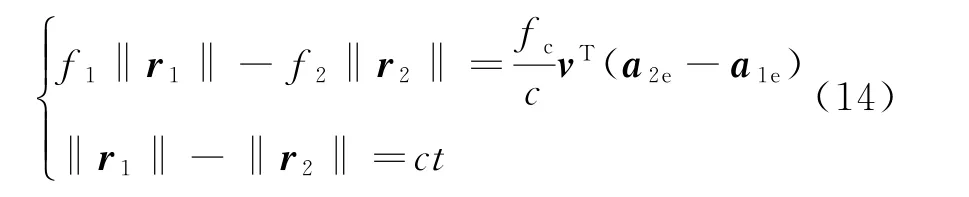
式(14)为双天线到舰船距离‖r1‖ 和‖r2‖的线性方程组。可以看出:当f1≠f2时,线性方程组可以求解出‖r1‖和‖r2‖的唯一解,不存在无根或多根的情况,能快速解算出双天线到舰船的距离;当f1＝f2时,式(14)无解,分为以下几种情况进行讨论。

(1)当双天线均位于卫星本体坐标系的Xb轴上时,双天线的坐标连线与卫星速度方向平行。由接收信号多普勒频率公式(6)～(8)可知,双天线分别到舰船位置的矢量与卫星速度方向的夹角相同,此时舰船位置应满足:在分别以2副天线的坐标为顶点、卫星速度方向为轴的2个圆锥曲面上。然而,这2个圆锥曲面没有交点。因此,双天线均位于卫星本体坐标系的Xb轴上时不存在定位无解区域。

(2)当双天线均位于卫星本体坐标系的Yb轴上时,因为卫星本体坐标系的Xb轴与质心轨道坐标系的Xo轴重合,双天线的坐标连线与卫星速度方向垂直,vT(a2e－a1e)＝0。此时,‖r1‖＝‖r2‖,定位无解区域为:通过双天线中线且垂直于双天线位置连线的平面与地球椭球面的交线。

(3)当双天线均位于卫星本体坐标系的Zb轴上时,双天线的坐标连线与卫星速度方向垂直,vT·(a2e－a1e)＝0。此时,‖r1‖＝‖r2‖。然而,分别以双天线坐标点为球心的2个球面的交线与地球的球面无交点,双天线的坐标点均在Zb轴上时不存在‖r1‖＝‖r2‖ 的情况。因此,双天线均位于卫星本体坐标系的Zb轴上时不存在定位无解区域。

上述理论分析表明:双天线均布局在Xb轴或均布局在Zb轴上时不存在定位无解区域。双天线均布局在Yb轴上时,星下点轨迹为定位无解区域。

1.3 舰船定位解算

舰船在地球上时,其坐标满足地球球面方程,见式(15)。

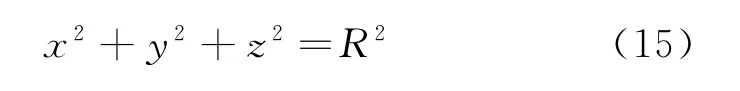
式中:R 为地球半径。

由此得出舰船位置的解算方程组为

求解式(16),可得到舰船位置在地固坐标系中的坐标u＝[x y z]T。

2 定位精度分析

在应用AIS双天线的舰船定位系统中,随机观测误差项主要有:在地固坐标系中,卫星位置误差d s,速度误差d v＝[d vXd vYd vZ]T;频率测量误差d f1和d f2,时差测量误差d t;双天线在卫星本体坐标系中的位置误差d a1b＝[d x1bd y1bd z1b]T和d a2b＝[d x2bd y2bd z2b]T。通过对舰船定位算法进行全微分运算,得出上述误差对舰船定位精度的影响,以下直接给出定位精度计算方法。

舰船位置误差d u＝[d x d y d z]T可表示为

双天线到舰船的距离误差d r＝[d‖r1‖ d‖r2‖ 0]T,表示为式(18);双天线在地固坐标系位置误差d a1e＝[d x1ed y1ed z1e]T和d a2e＝[d x2ed y2ed z2e]T,表示为式(19)。

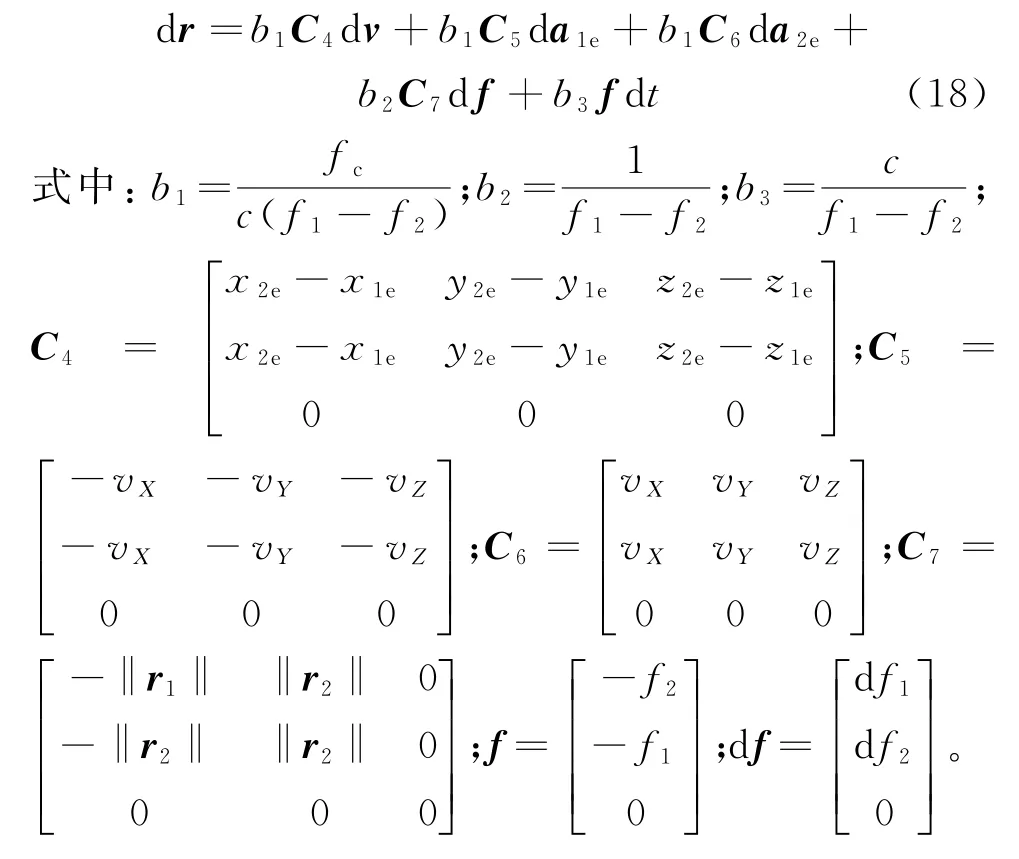
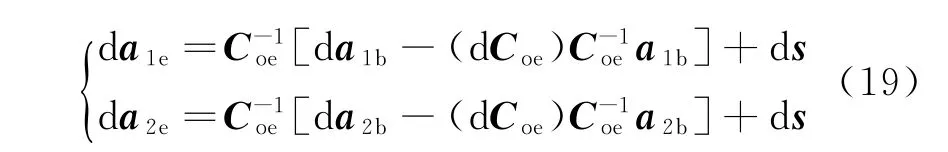
式中:地固坐标系到卫星本体坐标系的转换矩阵Coe＝CopCpe,其误差d Coe可表示为式(20)。

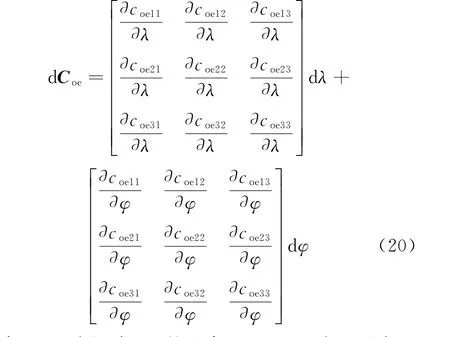
式中:coeij为矩阵Coe的元素;dλ 和dφ 为星下点经度λ 和纬度φ 的误差,由式(21)计算得出。

卫星经度、纬度和高度(h)的误差为

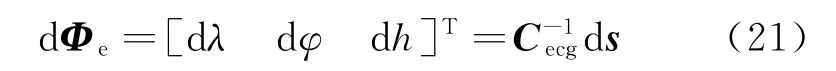
式中:Cecg为直角坐标系到经纬度坐标系的转换矩阵,可表示为式(22)。

式中:Rs为卫星到地心的距离。

3 算例验证

以500km高度的太阳同步轨道为例,利用STK软件生成卫星的位置和速度数据。地固坐标系下,卫星位置为[－486.679325 3055.706 775 6 142.846 891]T,单位km;星下点的经度为99.049°,纬度为63.252°;卫星速度矢量可表示为[3.401 513－6.054 058 3.281 013]T,单位km/s。假设定位解算中涉及到各参数的测量误差服从高斯分布的零均值随机误差,仿真算例采用的参数精度为:卫星位置精度为15 m;卫星速度精度为5 m/s;频率测量精度为1×10－3Hz;接收信号的时差精度为1×10－11s;双天线在卫星本体坐标系中的坐标为[1 0 0]T和[－1 0 0]T,单位m;双天线距离2 m;天线相位中心精度为0.01 m。运用蒙特卡罗重复试验方法,每点重复试验次数为100次,得出卫星覆盖范围内的定位误差分布,如图3(a)所示。采用第2节定位精度分析得出的理论定位误差,如图3(b)所示。

图3 仿真试验方法和理论计算方法对比Fig.3 Comparison of simulation and theoretical methods

对比图3(a)和图3(b)可见:蒙特卡罗统计所得定位误差分布与理论定位误差分布基本一致,验证了本文理论计算定位误差的正确性。

采用第2节的定位精度分析分别单独分析卫星位置精度、卫星速度精度、星载AIS接收机频率精度和时差精度、天线相位中心精度,以及双天线距离及安装位置对定位精度的影响。采用定位因子评估上述误差因素对定位精度的影响,定位因子定义为定位有效区域面积占总面积的比值,定位有效区域为满足目标定位精度小于目标斜距0.5%的区域[9-10]。具体分析结果如下。

(1)卫星位置精度从10 m 降低到20 m,定位因子保持在0.51,没有显著变化。

(2)卫星速度精度对定位因子的影响如图4所示。可以看出:速度精度从1 m/s下降到10 m/s,定位因子从0.50 下降到0.40。其中:速度精度从1 m/s下降到5 m/s,定位因子在0.50附近波动,没有显著变化,当速度精度进一步下降到10 m/s时,定位因子下降到0.40。因此,为保证定位因子达到0.50,卫星速度精度要小于5 m/s。

图4 卫星速度精度对定位因子的影响Fig.4 Influence of satellite velocity on positioning factor

(3)星载AIS 接收机频率精度从1×10－3Hz提高到1×10－5Hz[14],定位因子保持在0.51,没有显著变化。

(4)时差精度对定位因子的影响如图5 所示。时差精度从1×10－12s下降到1×10－10s[15-17],定位因子变化显著,从大于0.60下降到0.10以下。其中:时差精度大于1×10－11s时,定位因子下降剧烈。从图5可以看出:为保证定位因子达到0.50,时差精度应小于1×10－11s。

图5 时差精度对定位精度的影响Fig.5 Influence of time difference accuracy on positioning factor

(5)天线相位中心精度从0.010 0 m 到0.0001 m,定位因子保持在0.51,没有显著变化。

(6)双天线的距离对定位因子的影响如图6所示。双天线距离从1 m 增加到5 m,定位因子有一定的变化,从小于0.20 提高到大于0.60。从图6可以看出:为保证定位因子大于0.50,双天线距离应大于2 m。

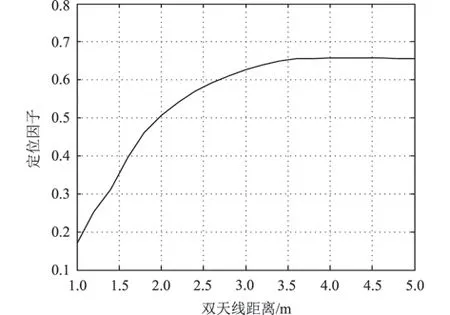
图6 双天线距离对定位因子的影响Fig.6 Influence of twin antenna distance on positioning factor

(7)双天线安装在不同坐标轴上对定位因子的影响见表1。因天线安装在卫星本体坐标系的－Zb轴上会受到卫星本体的部分遮挡而影响信号接收,表1中未考虑天线安装在－Zb轴上的情况。不同天线安装位置对应的定位因子介于0.26 和0.63之间。其中,定位因子大于0.50的天线安装位置为:①＋Xb轴和－Xb轴,即滚动轴正向和负向;②＋Xb轴和－Yb轴,即滚动轴正向和俯仰轴负向;③－Xb轴和＋Yb轴,即滚动轴负向和俯仰轴正向。星载AIS双天线的布局可优先选择上述3种位置。

表1 双天线安装在卫星本体坐标系不同坐标轴上对定位因子的影响Table 1 Influence of twin antenna position in different axes of satellite body coordinate system on positioning factor

综上所述,时差精度对定位因子的影响最为显著,双天线的距离和安装布局次之。卫星速度精度大于5 m/s时,影响较为显著;当精度小于5 m/s时,没有显著变化。卫星位置精度、星载AIS 接收机频率精度、天线相位中心精度对定位因子的影响没有显著变化。为保证定位因子达到0.50,各参数的测量要满足:①卫星速度精度小于5 m/s;②时差精度小于1×10－11s;③双天线距离大于2 m;④双天线优先选择安装在3种位置上(＋Xb轴和－Xb轴,＋Xb轴和－Yb轴,－Xb轴和＋Yb轴)。

4 结束语

针对仅接收1次AIS信号实现舰船快速定位的问题,本文提出了应用星载AIS双天线的舰船快速定位方法,通过同一信号多普勒频率、双天线接收时差与信号发送舰船的位置关系,实现天线到舰船距离的线性方程解算,提高了定位解算的速度。在此基础上,分析了卫星位置精度和速度精度、星载AIS接收机频率精度和时差精度、天线相位中心精度、双天线距离及安装位置对定位精度的影响。本文提出的方法适用于星上自主舰船目标识别,定位精度的影响因素分析结果可为星载AIS载荷指标的确定和双天线的布局提供参考。