桥梁结构多测组振型融合的两阶段快速贝叶斯方法研究
2021-08-21刘玲玲颜王吉任伟新
刘玲玲,颜王吉,李 丹,任伟新,秦 超
(1.合肥工业大学土木与水利工程学院,合肥230009;2.澳门大学智慧城市物联网国家重点实验室,澳门999078;3.澳门大学土木与环境工程系,澳门999078 4.深圳大学土木与交通工程学院,广东深圳518060)
模态参数识别是结构状态评估、有限元模型修正和损伤识别的基础[1]。环境激励下的模态参数识别方法具有无需贵重的激励设备、不影响结构的正常使用等特点,被广泛应用于工程实践中,主要分为时域法、频域法和时频域法等。其中,时域法主要有随机子空间法(SSI)、随机减量技术与特征系统实现算法的联合方法[2]和极点对称模态分解方法[3]等,频域法有频域分解法和振动响应传递比方法[4]等。
自然环境条件下桥梁结构的动力响应测试数据具有幅值小和随机性强的特点。与测试噪声及计算模型等因素有关的不确定性影响广泛存在于参数识别问题中[5-7]。因此,有必要在模态参数识别过程中考虑不确定性的影响。近年来,基于概率统计分析原理的贝叶斯理论在模态参数识别领域发挥了重要作用[8]。例如,Yuen和Katafygiotis[9]提出了基于贝叶斯模态参数识别的FFT 驱动方法,将模态域的结构模型嵌入到贝叶斯系统识别框架中,可识别出频率、阻尼比、振型等参数的最优值并量化其不确定性。贝叶斯FFT方法具有严格的理论推导,然而,其需要识别的参数过多,计算量巨大,不能直接应用于工程实际。为解决这一问题,Au[10]提出了快速贝叶斯FFT 方法,利用矩阵论和函数优化理论相关方法极大地降低了贝叶斯FFT方法对于优化和计算协方差矩阵的难度;Li 等[11]在贝叶斯FFT 方法中引入期望最大化算法,提高了其计算效率和鲁棒性。
振型可以提供桥梁结构变化的空间信息,在桥梁结构损伤识别和模型修正中具有重要价值。然而,在桥梁结构全尺寸环境振动实验中,因传感器数量不足以覆盖整个桥梁结构等原因,常需划分多个测组进行多次测试,如图1 所示。无法直接获得并处理全桥实测数据从而识别桥梁的整体振型。如何从各测组数据中准确地识别频率、阻尼比、局部振型,并利用局部振型准确地获得桥梁整体振型至关重要。“局部最小二乘法”与“整体最小二乘法”[12]等方法可快速获得整体振型,但都无法量化整体振型的不确定性。随后,Au等[13]提出了一种快速贝叶斯模态参数识别方法,通过融合各测组的FFT 信息求解整体振型。在Au 等[13]的基础上,Zhu 等14]引入期望最大化算法提高了振型最优值的计算效率,可适用于多模态甚至密集模态的情况。文献[15]在Au等[13]的基础上推导了Hessian矩阵的解析表达式,可进一步量化整体振型的后验不确定性。
针对桥梁多测组环境振动实验,本文提出了多次测试条件下桥梁振型融合的两阶段快速贝叶斯方法。首先,采用快速贝叶斯FFT 方法[10]求解各测组频率、阻尼比和局部振型的最优值及协方差。然后,基于贝叶斯原理[16-17]融合局部振型统计信息,通过解析迭代优化算法快速求解整体振型的最佳估计,并可计算负对数似然函数对整体振型的Hessian矩阵。该方法可利用局部振型的不确定性考虑各测组的数据质量的影响,并量化整体振型的不确定性。为验证该方法在实际桥梁结构模态分析中的有效性,对一座斜拉桥的实测数据进行了分析处理。同时,论文引入模态置信准则(MAC)概率指标[18],评估了整体振型的后验不确定性,并研究了各测组数据质量及频带宽度等因素对整体振型不确定性的影响规律。研究表明,采用该方法处理实桥数据效率高,且能合理地量化识别结果的不确定性。
1 多测组工况下的桥梁模态参数识别及振型融合问题
假设在桥梁结构环境振动实验中,共有nt个测组,测组i包含ni个测点,实验共nl个测点,每个测组至少有一个参考点与其他任意测组共享,则三者关系满足如图1所示,采集桥梁环境振动实验数据。桥梁模态参数识别及振型融合不确定性量化可分两个阶段实现:

图1 多测组环境振动实验测点布置及两阶段快速贝叶斯方法模态分析步骤示意图
(1)第1 阶段:运用快速贝叶斯FFT 方法识别各测组模态参数最优值及其协方差。识别参数包括:模态频率f、阻尼比ζ、局部振型ψ、模态激励的功率谱S及预测误差的功率谱σ2。此外,令∈Rni和Cψr,i分别表示测组i的第r阶模态局部振型最优值及其协方差,上标⌒表示参数最优值,并令m表示识别模态的阶数。
(2)第2阶段:运用振型融合的快速贝叶斯方法求解整体振型最优值及其协方差。令φr∈Rnl表示包含所有测点的第r阶模态整体振型,并令局部振型φr,i∈Rni表示φr的组成部分,对应测组i。
2 第1阶段:快速贝叶斯FFT方法
2.1 理论基础
假定一离散为nd个自由度的线性系统在环境振动试验中共有nl( ≤nd)个测点,分为nt个测组进行测量,每组共有ni个测点。对第i个测组加速度响应∈Rni建模可得:

其中:xj是第i组模型加速度响应,ej∈Rnl(j=1,2,…Ns)为预测误差,Ns为每个通道的采样数。待识别的模态参数为λθ={f,ζ,ψ,S,σ2}。xj的傅里叶变换为[10]

其中:i2=-1;Δt为采样间隔;Fk=Re ℱk,Gk=Im ℱk分别为的傅里叶变换ℱk的实部和虚部;k=2,3,…,Nq,对应的频率为fk=(k-1)/NsΔt,其中Nq=int[Ns/2]+1。
对于分离模态,假定在所选的频带内仅包含一阶模态。根据贝叶斯定理:

其中:c0是归一化常数为先验概率密度函数(PDF),在先验信息未知时,通常假定其为均匀分布[10,23]。由于该先验分布在后面推导的负对数似然函数式(8)中体现为一个常数,因而该假定并不影响整体振型最优值和协方差的求解。此时,参数后验PDF为[10]
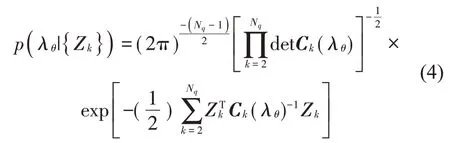
其中:Ck是Zk的协方差矩阵,其表达式为
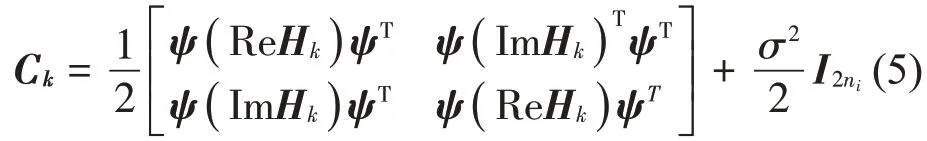
式中:ψ∈Rni×m为模态振型矩阵;I2ni∈R2ni×2ni为单位矩阵;Hk为模态响应的谱密度矩阵,其元素表达式为

式中:βik=f(i)/fk为频率比,f(i)、ζi分别为第i阶模态的频率和阻尼比,Sij为第i个和第j个模态激励间的互功率谱密度。
由式(4)可进一步推得后验PDF 与负对数似然函数成正比,即:
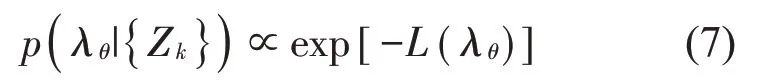
其中:L(λθ)为目标函数[10]:

式中:Nf为k的总个数其中:βk=f/fk;
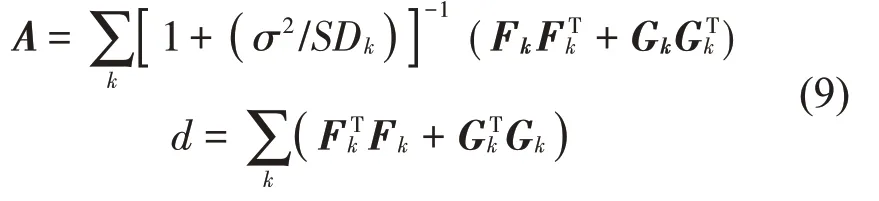
2.2 参数的最优值及其后验不确定性
对式(9)中矩阵A进行特征值分解,其最大特征值所对应的特征向量即为振型ψ的最优值,进而求出归一化的振型最优值/‖ψ‖。
将式(8)关于ψ最小化[10]:
后验协方差矩阵等价于负对数似然函数L(λθ)的Hessian矩阵的逆矩阵[10]。局部振型的协方差矩阵Cψr,i为中对应于振型ψ的ni×ni阶方阵[19]。
通过上述快速贝叶斯FFT方法可求出各测组频率、阻尼比、局部振型的最优值及其协方差矩阵。假定任意测组局部振型的PDF 近似服从高斯分布[16,20],则对于局部振型φr,i∈Rni,其概率分布公式为
其中:N为正态分布符号。
3 第2 阶段:快速贝叶斯振型融合方法
3.1 局部振型与整体振型的关联

其中:Li∈Rni×nl,若第i个测组的第p个测点对φr的第q个自由度有贡献,则元素Li(p,q)=1,否则为0。
识别的局部振型已对其欧几里得范数归一化,同样地,将φr,i对其欧几里得范数归一化:

在2.2 节中已说明,测组i的局部振型可通过高斯分布很好地近似,则以φr表示并反映(,Cψr,i)贡献的似然函数为[16,20]
在式(14)中已省略与φr独立的归一化常数。
3.2 整体振型后验概率密度函数
根据贝叶斯定理,整体振型φr的后验PDF如下:
其中:℘={,Cψr,i:i=1,…,nt},c1是归一化常数;p(φr)为先验PDF。假定从不同测组中识别的局部振型在统计上是独立的,因而反映℘贡献的似然函数如下[16]:

假定p(φr)为均匀分布,φr的后验PDF 满足p(φr| ℘)∝exp(-Las(φr)),Las为目标函数[16]:
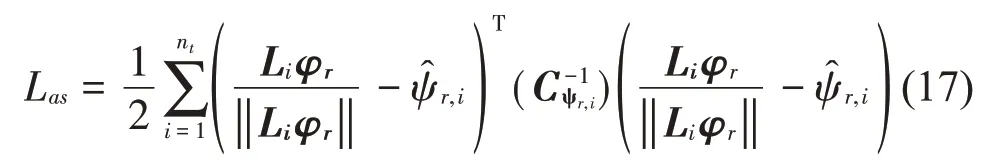
式(17)中的整体振型φr受到约束条件φrTφr=1 的限制。
当局部振型协方差矩阵为单位矩阵I∈Rni×ni时,每个测组分配的权重相同,此时,目标函数简化为

“整体最小二乘法”[12]是通过已识别的局部振型和待识别整体振型之间的平方差构造目标函数,为所有测组分配相同的权重,其目标函数与式(18)一致。当假定局部振型协方差矩阵为I∈Rni×ni时,即不考虑局部振型的协方差时,该表达式退化为“整体最小二乘法”。因此,快速贝叶斯振型融合方法是对整体最小二乘法的延伸,它可利用局部振型协方差考虑不同测组数据的不确定性信息。
3.3 最优值与协方差矩阵的求解
最小化式(17)即可求解φr的最优值。引入辅助变量其中i=1,2,…,nt,在的约束条件下,利用拉格朗日乘数法,式(17)可变换为[16]

其中:γr、βr,i(i=1,2,…,nt)均为拉格朗日乘子,分别使得约束条件‖φr‖2=1和成立。
3.3.1 整体振型最优值
式(19)中待识别的参数为λas={φr,γr,βr,i,χr,i:i=1,2,…,nt}。直接求解参数最优值的计算过程具有高维及非线性特征,因而采用迭代求解策略计算。分别求出χr,i、βr,i、φr和γr最优值的解析表达式,然后通过线性迭代优化算法确定其最优值[16]。
(1)χr,i和βr,i最优值:
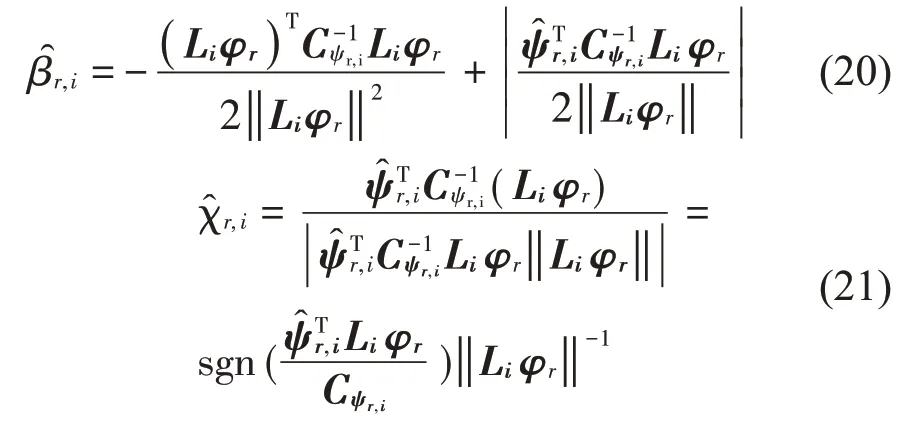
其中:sgn( ∙ )表示符号函数。
(2)φr和γr的最优值:

其中:
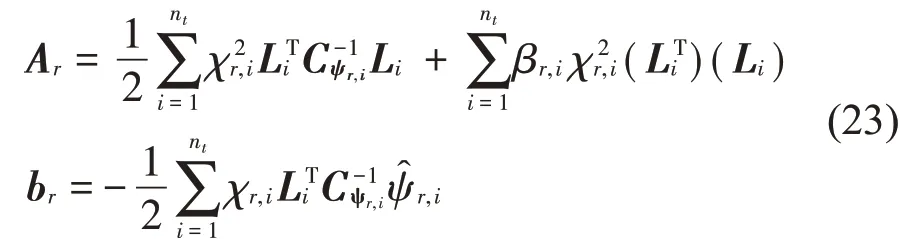
3.3.2 整体振型后验不确定性
整体振型φr的不确定性近似服从以参数最优值为中心的高斯分布。将目标函数式(17)中的整体振型归一化,即可得:

令表示式(24)在最优值处求得的Hessian 矩阵,其表达式为[17]:


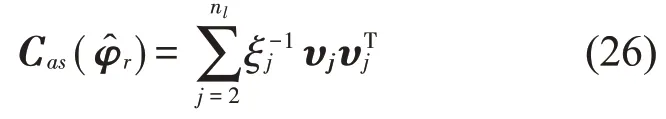
为整体评估最优整体振型的后验不确定性,本文引入MAC概率指标[18],用来衡量振型变量φr与振型最优值之间的相似性。当φr的不确定性越小时,φr越接近于,计算的MAC 值越接近于1,为计算方便,选择计算φr的期望及之间的MAC 值。该指标的近似解析表达式为[17–18]
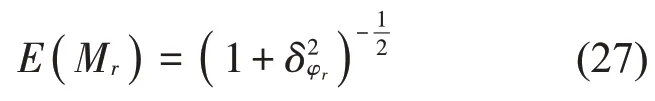
4 计算流程
针对桥梁结构分组多次测试的环境振动试验,两阶段快速贝叶斯方法的计算过程如图2所示。

图2 2阶段快速贝叶斯方法的计算流程
5 实桥分析
常德白马湖公园虹桥是一座4跨曲线钢箱梁斜拉人行桥,全长120 m,跨径布置为27 m+33 m+33 m+27 m,如图3 所示。该桥的环境振动实验分为8个测组,每组共有12个测点。其中竖向测点有6个,布置在桥梁两侧;横向水平测点有3 个;全桥共设置3 个参考点,布置在中跨跨中附近偏向中墩侧的断面处。全桥加速度传感器布置情况如图4 所示。分组情况见表1。实验采样频率为500 Hz,采样时长为15 min。实测的详细方案参见文献[21–22]。

表1 测点分组布置

图3 虹桥实景图
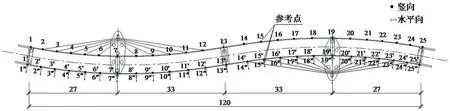
图4 桥面测点布置图[22]
采用快速贝叶斯FFT方法识别模态参数时需要先选取频带。假定在所选频带中仅包含1 阶分离模态,并以频率初始值为中心选取频带,范围为f0(1±κζ0)[10,23],此处f0和ζ0分别为频率和阻尼比的初始值,κ为频带宽度[23]。如图5所示。

图5 第2测组功率谱图
本文选取各阶模态频率初始值f0分别为3.784 Hz、4.761 Hz、5.981 Hz、6.470 Hz,设各阶模态频带宽度κ为2,并取各阶模态初始阻尼比ζ0为0.01。首先求解振型ψ的最优值,并通过解决一个数值优化问题来确定f、ζ、S和σ2的最优值,然后计算参数的后验协方差矩阵,并从中提取局部振型协方差矩阵Cψr,i。利用SSI 和快速贝叶斯FFT 方法识别的前4阶竖向模态频率及阻尼比值如表2所示。2种方法识别的频率值基本一致,阻尼比值也很接近,由此可见,采用快速贝叶斯FFT 方法识别频率和阻尼比的精度较高。第5、7列为采用快速贝叶斯FFT方法识别的频率及阻尼比的变异系数,前4 阶竖向模态频率变异系数最大为0.12%,不确定性很小,而阻尼比变异系数最大达到15%,不确定性较大。在识别得到局部振型最优值及其协方差矩阵后,在参数最优值解析表达式的基础上,通过线性优化迭代算法快速计算整体振型的最佳估计,并计算负对数似然函数对整体振型的Hessian 矩阵,以量化整体振型的不确定性。整个计算过程包含2 个阶段,每个阶段的计算时间均不超过2 min,其中,从单个测组数据中识别每阶模态的运算可在几十秒内完成。

表2 模态识别结果对比
图6 为采用贝叶斯振型融合方法识别的前4 阶竖向模态整体振型图。以1-E(Mr)评估局部振型及整体振型的不确定性,不同测组局部振型不确定性及整体振型不确定性的评估结果如表3所示。将不同测组的局部振型不确定性变化绘于图7,其中实线代表不同测组局部振型不确定性,虚线代表整体振型不确定性。局部振型不确定性可表征各测组数据的质量,在振型融合过程中,各测组间相互影响,数据质量差的测组将会干扰数据质量好的测组,因此应被分配较小的权重。由图7 可见,个别测组的局部振型不确定性较大,而对应的整体振型不确定性有所下降,表明数据质量差的测组被赋予的权重较小,从而有效地抑制了它们带来的影响。由图7(c)和图7(d)可知,相比第4阶模态的测组2,快速贝叶斯振型融合方法对第3 阶模态的测组3 和6 的识别结果的“抑制作用”更为明显。其主要原因是,对第3阶模态,由测组3和6所识别的局部振型不确定性相对其余测组很大,其被分配权重更小,因而对整体振型识别的影响更小。

表3 各测组局部振型及整体振型不确定性评估(×10-4)

图6 前4阶竖向模态整体振型图
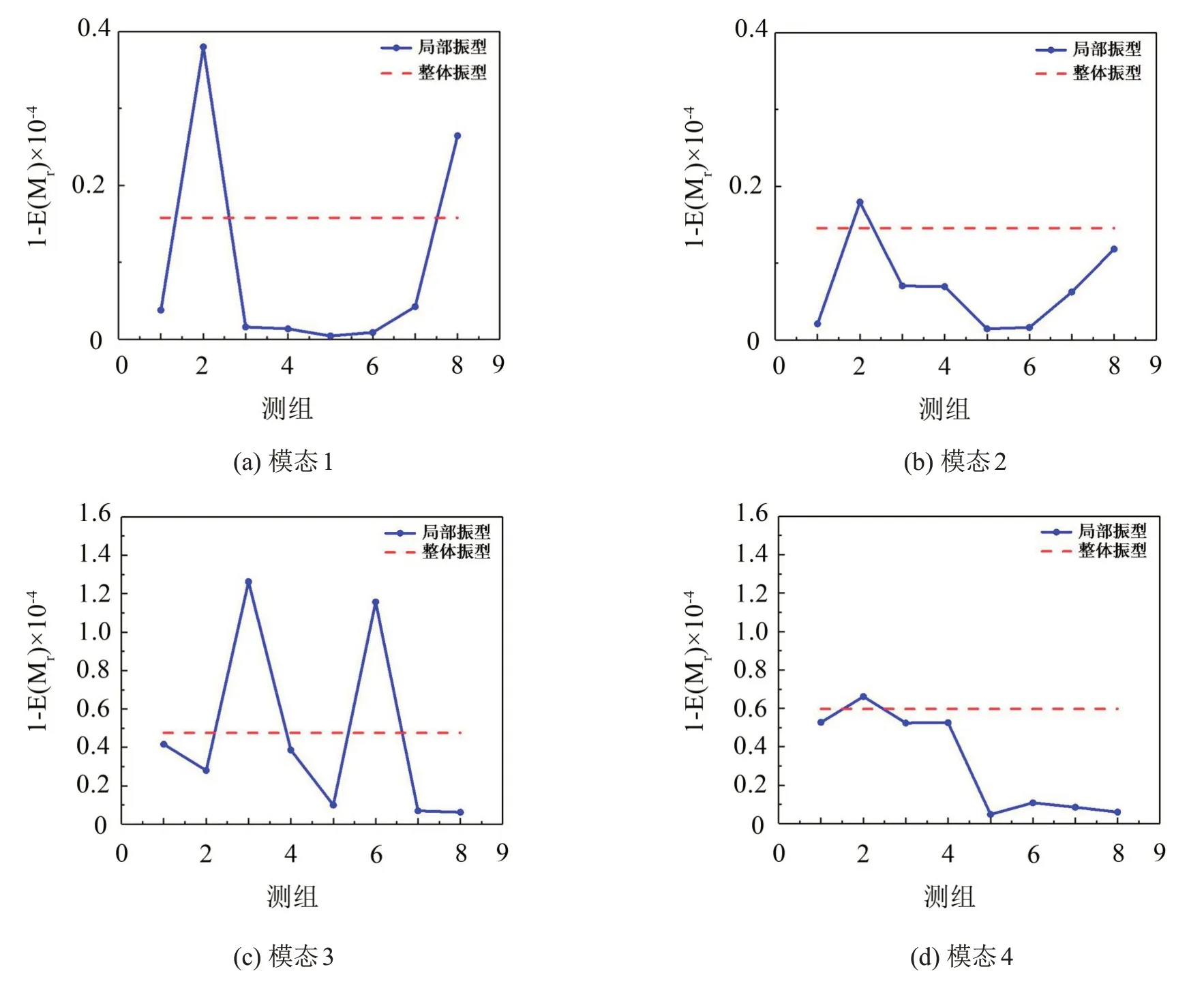
图7 前4阶竖向模态各测组局部振型不确定性变化图
为研究频带宽度对振型识别结果的影响,设定频带宽度参数的变化范围为κ=1,2,…,6。整体振型不确定性随频带宽度增加的变化趋势如图8 所示,虹桥前2 阶竖向模态的整体振型不确定性随宽度的增加而减少。而第3、4阶竖向模态的整体振型不确定性为先减少而后有所增加,在频带宽度为3时,其不确定性最小。整体振型不确定性在初期随频带宽度增大而减小,主要原因是频带宽度越大,数据信息越完备,识别结果的不确定性就越小。而第3阶和第4阶模态整体振型不确定性在后期随频带宽度增大呈增大的趋势,主要原因为频带越宽,模态激励和预测误差的平谱假定及频带内单个模态假定等越不满足,建模误差越大。因而在桥梁工程实际应用中,需要在两者之间进行权衡,以选择最优的频带宽度。
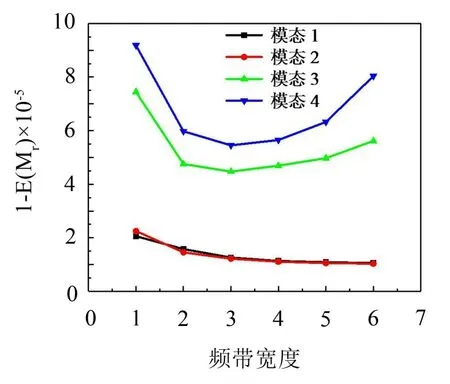
图8 频带宽度分析
6 结语
本文提出了桥梁结构多测组振型融合的两阶段快速贝叶斯方法。第1阶段采用快速贝叶斯FFT方法求解各测组局部振型的最优值及协方差;第2 阶段利用局部振型的协方差,基于快速贝叶斯振型融合方法有效量化整体振型的不确定性。最后通过一座斜拉桥的环境振动实测数据验证了该方法的有效性。研究所得结论主要包括:
(1)采用快速贝叶斯FFT 方法可以快速识别频率、阻尼比等模态参数的不确定性。实桥分析表明,频率变异系数最大为0.12%,表明其不确定性很小;而阻尼比变异系数可达到15%,表明其不确定性非常明显。
(2)快速贝叶斯振型融合方法通过解析迭代优化算法快速求解整体振型的最优值,通过负对数似然函数关于整体振型的Hessian矩阵的解析表达式,可实现快速计算并量化整体振型不确定性。该方法利用局部振型协方差矩阵自动分配不同测组的权重,有效地考虑了不同测组数据中包含的不确定性信息。
(3)实桥结果表明,快速贝叶斯振型融合方法在振型融合过程中能有效抑制数据质量较差测组的影响,且对数据质量相对越差的测组,其“抑制作用”越明显。所识别的整体振型及其不确定性可进一步应用于考虑不确定性影响的桥梁结构损伤识别及模型修正等方面。
(4)实桥分析表明,存在若干阶模态的整体振型不确定性随频带宽度增大的变化趋势为先减小而后增大。整体振型不确定性在初期逐步减小,主要原因为频带宽度越大数据信息越完备;整体振型不确定性后期逐渐增大,主要原因为频带越宽使得模态激励和预测误差的平谱假定及频带内仅包含单个模态的假定等越不满足,导致建模误差增大。致谢:
感谢任伟新教授课题组参与白马湖虹桥动力测试工作的所有研究生,感谢李志刚和魏锦辉博士在数据分析中提供的帮助和支持。
