MAGNET 电磁场仿真在复杂干式变压器阻抗计算中的应用

张春喜 何啸雷

摘要：利用专用的电磁仿真软件MAGNET 对轴向双分裂和大容量等复杂干式变压器进行了不同运行工况下的磁场分析和验证。基于场路耦合法根据需要模拟的工况建立合适的2D 或3D 等效模型，并利用正确的等效电路和边界条件对变压器的运行工况进行有限元分析模拟，最终通过能量法或电压法得到相应工况下变压器的阻抗。实际测试结果表明该方法的计算精度可满足产品实际要求，可使用MAGNET 对干式变压器的阻抗进行仿真计算和设计改进。

关键词：MAGNET;电磁场;仿真;干式变压器;阻抗;计算

中图分类号：TM412文献标志码：A文章编号：1009-9492（2021）12-0235-04

The Application of MAGNET Electromagnetic Simulation in Impedance

Zhang Chunxi，He Xiaolei

（ Siemens Transformer （ Guangzhou ） Co. ，Ltd. ，Guangzhou 510530，China ）

Abstract：The magnetic field of axial split and big rating dry-type transformers under different operating conditions was analyzed and verified by electromagnetic simulation software MAGNET. The equivalent 2D or 3D model was created on basis offield-circuit coupled method according to the operating conditions to be simulated，finite element analysis was used to simulate the operating conditions according to correct equivalent electricity circuit and boundary conditions，the corresponding impedance was obtained by means of energy method and voltage method. The effectiveness of simulationresultisverifiedinpracticebycomparingtheactualmeasuredvalues，theimpedancecalculationanddesign optimization can be implemented with MAGNET simulation results.

Key words：MAGNET;electromagnetic field;simulation;dry-type transformer;impedance;calculation

0 引言

干式变压器的阻抗是一个重要的产品参数，既关系着变压器二次侧的实际输出电压值，又是变压器所在电力系统中保护装置选型的重要依据，因此变压器设计时对阻抗的计算精度要求较高。传统的阻抗工程计算公式[1]对于普通变压器比较适用，其计算精度基本能满足产品的实际使用，但其计算模型用于漏磁场复杂的产品时计算值与实测值相差较远。近年来对于轴向双分裂、移相整流及大容量等变压器的阻抗计算有一些公司根据理论分析或实测数值尝试使用额外的系数对计算结果进行修正，也有不少公司开始使用计算机仿真的手段对这些具有复杂漏磁场的产品阻抗进行有限元计算[2-8]，但要么是针对高电压等级的油浸式电力变压器，要么是籠统介绍如何使用有限元方法或自编软件进行阻抗计算，亦或是单纯介绍软件的使用方法，没有具体介绍如何使用特定软件结合干式变压器的结构进行阻抗仿真计算。王耀强[9]介绍了基MAGNET 对一台大容量干式变压器关于三维建模及网格处理的方法，但未对二维模型法及双分裂产品不同工况的漏磁场模拟仿真进行说明。

为提高具有复杂漏磁场干式变压器的阻抗计算精度，本文介绍了如何使用MAGNET 电磁仿真软件对于干式变压器建立模型、场路耦合分析、阻抗计算等，并通过实际产品对结果进行了验证，为MAGNET 在干式变压器阻抗准确计算提供了有力的帮助。

1MAGNET 在阻抗仿真领域的应用

1. 1用MAGNET 创建干式变压器仿真模型

MAGNET 仿真模型可基于2D 或3D 进行创建，针对干式变压器阻抗的仿真，其主要区别如下。

（1）2D 仿真基于平面建模，无法对三相工况进行仿真模拟，其模拟只能基于单相进行，且2D 仿真由于软件本身的限制，需要手动限定仿真边界条件，以此得到更加准确仿真结果。但优点是建模简单，只需要在二维平面对单相系统的二分之一切面进行建模即可进行仿真运算。同时网格划分数量少，运算量小，仿真速度快，可快速得出结果。

（2）3D 仿真基于三维建模，配合适的电路连接，理论上可对变压器任何工况进行仿真模拟，其边界条件常规情况下无需手动给定边界，软件可根据实际使用材料自行判断。但3D 仿真同时存在一些不足：建模复杂困难，耗时长。由于模型本身特性，其仿真结果精确度较二维低，原因是仿真过程中，三维模型存在的磁场畸变较二维模型大，导致计算结果会因此出现偏差，虽可通过增加网格节点数量，增加节点公式的级数来进行改善，但此方式会极大地增加运算量，耗时更久。

常规情况下，仿真建模应优先使用2D 仿真单相建模，主要考虑其建模简单、精准度高、运算速度快的特点。网格的划分亦会极大的影响最终的结果，如果网格节点过高会造成无法有效收敛，从而导致计算耗时大幅加长的情况。根据经验，大部分情况下可使用MAGNET 的自适应网格功能，无需指定大小。当精度要求较高时，网格大小建议不超过最长边界的10%。

1. 2 2D 模型创建及仿真

以下以一台特殊的变频变压隔离变压器（以下简称例A）为例，其容量为2500 kVA，一次侧电压为10 kV，低压侧分别主600 V 和400 V，阻抗电压要求为8%，联结组别为DDODYN11，其工作频率分别为50 Hz 和60 Hz。对其在不同频率（50 Hz 和60 Hz ）、不同工况下绕组磁场分布和短路阻抗等电磁特性参数进行数值仿真计算、分析和验证。

变压器绕组的布置为：辐向由内至外，铁心-低压侧-高压侧，低压线圈两个，轴向上下排列，线圈结构相同，串联连接。低压线圈为星接，高压线圈为角接。MAGNET 仿真计算基于以下关键信息和前提创建其2D 模型。

（1）低压线圈有2个轴向散热气道，为保证仿真准确性，建模时需要将低压线圈进行多段切割，以模拟气道的存在。由于气道会增加变压器的漏磁，理论上带气道模型阻抗会比不带气道模型更大。

（2）假定电流在绕组内（导体内）均匀分布，系统不存在涡流效应的影响。模型材料按照材料本身特性决定线性或非线性类型。

（3）铁心的磁导率远大于包裹导体的绝缘材料和空气，故模型的仿真边界取FIELD NORMAL。即原理上认为，磁力线遇到上下铁轭后，其切线分量转变为零，从能量上理解，即无能量回馈至线圈系统。

（4）此变压器三相电流对称，三相绕组结构一致。故模型建模可使用单相建模，无需使用三相建模。

（5）此台变压器为隔离变，其运行工况包含两组不同电压和频率，低压侧为输入端，高压侧为输出侧。

创建的2D 模型如图1所示，对图中的二维模型模拟实际工况由外部电路进行驱动，电路为由电源、线圈、电感、电阻等电气电子元件组成的耦合电路。MAGNET 根据驱动电路和二维建模，通过计算空间内的矢量场进行线圈磁场的仿真，以此得到系统在空间内的磁场分布和系统内闭合回路电压、电路的数值。

1. 3 3D 模型创建及仿真

以下以一台特殊的轴向双分裂变压器（以下简称例B）为例，其对其在不同工况下绕组磁场分布和短路阻抗等电磁特性参数进行数值计算，分析和验证。该变压器其辐向由内到外分别为：铁心、低压线圈、高压线圈。其中低压线圈为轴向双分裂，上线圈为星接，下线圈为角接，电气上为独立系统。高压线圈上下线圈均为角接，整体电气连接为并联。例B上下系统容量相异，上系统容量仅为下系统容量的40%。基于下述信息和预设前提在MAGNET 中创建3D 模型。

（1）此变压器三相的结构相同。此变压器为不带外壳的干式变压器（带外壳屏蔽情况不在本文考虑），故其工况运行时，周围边界条件为无限源空气包。变压器按照实际尺寸简化后1比1建模，低压线圈建模包含气道，增加仿真结果的精确性（原理见例A 描述说明）。

（2）模型不考虑涡流的影响，电流在绕组内均匀分布。计算特性按照材料本身特性决定。

（3）边界条件为无限源边界条件，变压器运行在巨大的空气包裹的三维空间内。

（4）工况运行时，三相电源对称。但考虑特殊运行工况时，安匝分布和漏磁场分布不对称的影响，故使用三维方式对三相建模仿真。

（5）仿真包含3种工况：一是全穿越运行，即上下系统均处于运行状态，此时高压侧给电，低压侧D接和Y 接同时处于短接;二是半穿越运行，即上下系统其中一个处于运行状态，此时高压侧给电，低压侧任一系统短接，另一系统开路;三是分裂运行，即低压侧任一系统给电，低压侧另一系统短接，高压侧开路。

创建3D 模型如图2所示，图中变压器计算模型的外侧轮廓线可视为其空气边界。根据其产品结构及上文描述的不同运行工况，用MAGNET 建立不同的驱动电路进行仿真计算。

2 計算结果和分析

在MAGNET 中创建好产品模型后利用软件进行场路耦合和有限元分析模拟。MAGNET 仿真并不能直接显示系统的阻抗值，需要根据电磁场能量法和模拟试验操作的电压法，根据数据进行一定后处理才能得到结果。以下简单介绍电磁场能量法的算法原理和模拟试验操作的电压法计算原理。

2. 1阻抗计算方式

通用的阻抗计算方式主要有两种，但本身均存在一定局限性，故实际应用中，应采取两种并施的方式。大多数情况下，当两种计算方式数值差距不大时，仿真值的准确度最高。

2. 1. 1 能量法计算方式说明

能量法用MAGNET 根据模型在运行状态下的磁场能量值计算阻抗，其计算基于以下3个公式[3]：

通过以上3个基准公式，可以得到基于线圈能量计算阻抗的通用公式，如下：

式中：U 为变压器阻抗，Ω;U%为变压器阻抗标幺值，pu;I 为变压器相电流，A;L 为线圈电感值，H; S 为运行工况下的单相容量，kVA;F 为运行工况下的频率，Hz;W 为线圈蕴含的磁场能量，J。

2. 1. 2 电压法计算方式说明

电压法基于MAGNET 计算得出的各节点电压值来推导变压器的阻抗值。电压法的优点在于其驱动电路接线与产品试验实际测试时一致，故理论上会更加接近实测值。且由于MAGNET 可直观地观测到感应线圈两端的电压值，故在计算时拥有便利性。但其缺点也很明显，即在3D 仿真情况下，由于软件参照的是理想状态，三维空间内的网格会存在扭曲的现象（此现象理论上存在于所有的仿真软件，可配合特定点的网格精度调整进行修正，本文不详述），在特殊情况下会造成仿真结果并不准确的情况。电压法的阻抗计算公式如下：

U%=（V感应电压/V额定电压）×100 （5）

2. 2例A 计算和分析

例A 变压器在MAGNET 中的网格划分如下，网格大小按照1. 1节所述，对铁心和线圈进行10%网格划分，空气边界部分使用MAGNET 自适应网格。该模型的网格划分及运算后的磁场矢量图和云图如图3所示。

根据MAGNET 仿真计算的结果，提取阻抗计算相关的数据为：线圈磁场能量分别为118. 44 J （频率为60 Hz 时）、143. 01 J （频率为50 Hz 时）;线圈低压线圈的感应电压分别为254. 5 V （频率为60 Hz 时）和234. 11 V （频率为50 Hz 时）。

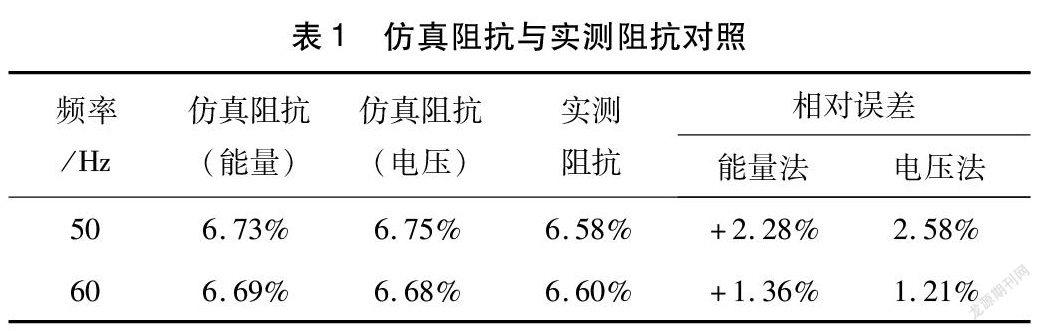
根据式（4）和式（5）进行计算。能量法计算阻抗：6. 69% （频率为60 Hz 时），6. 73% （频率为60 Hz 时）;电压法计算阻抗：6. 68% （频率为60 Hz 时），6. 75% （频率为60 Hz 时）。

与实测值的对比如表1所示。

对于例A 变压器，可发现其实测值在两种不同工况下，仿真模拟的阻抗值均比实测值略大一些，这是由于在实际生产和装配过程及试验测量过程中均会存在一定的误差，且仿真过程中也会存在网格划分精度等影响仿真结果的因素造成的。同时结合大量的产品实测值和仿真值对比，可发现对于此类型双绕组变压器仿真的结果误差可控制在±3. 5%范围内，可充分满足实际产品的运行要求。

2. 3 例B 计算与分析

例B 的轴向双分裂变压器的网格划分如图4所示，仿真运行后对应的磁场云图如图5所示（仅截取单相X、Y 轴方向图）。

根据式（4）和式（5）计算阻抗，其在各种工况下模拟的阻抗值和实测值对比如表2所示。由表可知，不管是能量法还是电压法，其仿真阻抗结果的误差均可控制在±2. 5%内。

此外MAGNET 的电磁场仿真同时可以用于仿真系统在不同工况下的电流分布情况，如例B的半穿越电流仿真值与实测值的对比值如表3所示。

对比常规所用的通用算法[1]配合修正系数[4]，其适用范围更加广泛，且准确度较高。仿真结果不仅可用于估计阻抗的具体值，亦可用于分析此工况的线圈电流分布和漏磁情况，为后续漏磁造成的线圈局部热点提供参考。

3 结束语

在针对特殊变压器时，结合变压器运行工况和其特殊的结构特点，利用MAGNET 进行建模可通过有限元方法对变压器在实际运行工况条件下的状态进行模拟仿真，从而得出较为准确的参考值以协助设计。从结果上看，本文通过对例A （双工况运行多绕组变压器）和例B （非等容量轴向双分裂变压器）进行二维和三维磁场模型的耦合计算，得到仿真的变压器阻抗和电流分布的参考值，不管是2D 法和3D 法其结果与实测值的对比均可将误差控制在3%以内，当两者结果一致时其准确度更高，因此可表明MAGNET 在具有复杂漏磁场的干式变压器阻抗模拟仿真领域可为变压器的设计提供可靠的参考。MAGNET 电磁仿真除了对变压器进行阻抗模拟计算外，还可以进一步用来研究分析漏磁场引起的杂散损耗，从而避免结构件局部过热并降低产品成本。

参考文献：

[1]路长柏. 电力变压器理论与计算[M]. 沈阳：辽宁科学技术出版社，2007.

[2]周少静，王建民，王浩名，等. 大容量移相整流变压器电流分布和短路阻抗的数值计算[J]. 电力科学与工程，2013，29（4）：30-34.

[3]李岩，李龙女，井永腾，等. 轴向双分裂发电机变压器漏磁场及穿越短路阻抗计算与分析[J]. 高电压技术，2014，40（6）：1623-1629.

[4]贾贺强，谭黎军. 轴向双分裂结构变压器阻抗计算的修正系数和分裂系数分析[J]. 变压器，2005，42（11）：1-4.

[5]景崇友，王建民，王永表，等. 大型变压器漏磁场及特性参数的工程仿真软件研发[J]. 变压器，2008，45（4）：1-5.

[6]徐曙光，周广宇，苏宝国，等. 轴向双分裂变压器的电场计算和漏磁计算[J]. 变压器，2010，47（6）：5-9.

[7]谢若冰，陈乔夫，李晓松，等. 用三维有限元法计算分裂式变压器短路阻抗[J]. 高电压技术，2007，33（6）：97-101.

[8]郭健，林鹤云，徐子宏，等. 基于能量摄动法的变压器短路有限元计算[J]. 电气应用，2007，26（9）：34-36.

[9]王耀强. 变压器阻抗有限元的仿真计算[J]. 中国特技信息，2016，31（9）：95.

第一作者简介：张春喜（1982-），男，大学本科，工程师，研究领域为配电变压器技术、工艺及材料。（編辑：王智圣）