基于深度学习的物体点云六维位姿估计方法

李少飞，史泽林，庄春刚

（上海交通大学机械与动力工程学院，上海 200240）

0 概述

散乱场景中的三维物体拾取是机器人操作中的一类经典问题，利用机械臂将箱子中无序摆放、堆叠的物体取出对机器人实现自动化具有重要意义。该问题的难点在于散乱堆叠的物体之间存在大量的遮挡，这不仅影响了对物体的识别，而且使得拾取过程中的碰撞检测更加复杂。物体六维位姿识别是散乱场景中三维物体拾取的重点和难点。近年来，深度学习技术在六维位姿估计任务中得到广泛应用。文献［1-3］根据RGB 数据对纹理丰富的物体实例进行六维位姿估计。文献［4］扩展二维目标检测器，提出一种基于分类离散视点的旋转位姿估计方法，但该方法仅预测真实姿态的粗略离散近似值，为达到更好的效果，还需对输出结果进行位姿细化。文献［5］先将RGB 图像在2 个网络中进行由粗到细的分割，再将分割结果反馈给第3 个网络得到待检测目标边界框点的投影，最终利用PnP 算法估计六维位姿，但该方法由于将网络分为多个阶段，因此导致运行时间非常长。文献［6］针对通过CNN 检测二维关键点并利用PnP 回归六维位姿的方法在遮挡和截断样本中存在的问题进行改进，对于每一个像素计算一个指向二维关键点的方向向量，并通过投票策略得到鲁棒的二维关键点，减少了物体局部缺失对位姿估计的影响。文献［7］通过训练获取输入RGB 图像的六维隐变量表示，然后在数据库中查找和其最相近的位姿作为估计结果。然而，在低纹理的情况下，仅通过RGB 信息估计的六维位姿准确率较低。文献［8-10］将RGB 信息和深度信息相结合估计目标的六维位姿。文献［11-12］均是利用CNN 学习特定的描述子进行目标检测和六维位姿估计。从RGB-D图像进行六维目标位姿估计的关键是充分利用两个互补的数据源，文献［13］提出一种新的稠密融合网络，该网络将分别处理后的两种数据源进行像素级别的特征嵌入，从而估计出物体的六维位姿。

近几年，基于深度学习的六维位姿估计方法多数将RGB 图和深度图作为输入。然而，一个物体处于不同的位姿却有着相似的二维图像这一现象是很常见的，这限制了基于二维图像的位姿估计的准确率。在一些工业应用中，为了获取完整场景、高精度的三维信息，通常会采用三维扫描仪获取场景点云，而有些扫描仪由于成像原理不同，不能获取RGB 图和深度图。随着传感器技术的发展，获取三维点云的速度得到了大幅提升，这使得基于点云研究的实时性得到了保障。因此，基于点云的物体六维位姿估计引起了研究人员的关注。DROST 等［14-15］提出基于物体点对特征（Point Pair Feature，PPF）的位姿估计算法及其变体算法，并将其成功应用于工业机器人分拣任务，然而此类算法的局限性在于：一方面，如果模板点云和场景点云的采样疏密程度不一致，将难以发现相似点对特征，从而导致匹配错误；另一方面，出现了一些先分割后配准的算法，将点云进行聚类分割后，利用点云配准的流程得到物体的位姿［16］，但是此类算法计算量大，且在堆叠严重的场景中表现较差。在深度学习领域，QI 等［17］基于对称函数思想，将原始点云输入网络进行训练实现分类和分割任务，并在网络中加入分层多尺度特征学习［18］，该方法相比已有方法在精度上有了显著提升。之后研究人员将该方法应用于自动驾驶的目标检测提出F-PointNet［19］，F-PointNet 虽然在一定程度上解决了三维目标检测问题，但是激光雷达获得的点云是稀疏和不规律的，在自动驾驶场景中的物体也鲜有遮挡的情况，并且包围框的位姿也仅考虑垂直于地面的旋转，这与散乱场景中堆叠的工件有很大的差别，因此此类方法的实用性不强。

针对现有点云位姿估计方法计算量较大且在复杂场景中结果鲁棒性较差的问题，本文提出基于深度学习的物体点云六维位姿估计方法，将三维点云映射到二维平面，生成深度特征图和法线特征图，提取位姿特征。

1 数据集生成

1.1 工业零件建模

现有基于深度学习的六维位姿估计方法多数是在已有的LINEMOD、OCCLUSION 等数据集上进行测试。但是，由于工业零件的特殊性，在这些数据集上测试效果很好的神经网络并不能适用于一些低纹理的机械零件，因此本文提出了一种用于工业零件位姿估计的数据集生成方法。

在对数据集进行标签标注时，点云的标签标注相比二维图像标注更加困难。每训练一个新的工件，如果用真实点云生成数据集，则工作量会非常巨大，因此在仿真环境下生成数据集用于训练是很有必要的。文献［20］考虑了环境光反射的影响，利用Unity3D 游戏引擎生成散乱堆叠场景的深度图数据集。文献［21］利用Blender API 将提前建好的日常用品的三维模型放入仿真环境，设置模型初始位姿，并通过重力掉落以及刚体碰撞模拟真实环境。上述仿真方法均能达到较好的效果，但是所仿真模型的几何结构都是类似于圆柱体、立方体等简单的模型，而对于一些复杂的工件，首先建模精确度较低，其次仿真会出现穿模现象。

本文对文献［21］所采用的物理仿真方法进行改进，在Blender API 中根据模型纹理、矩形包络、球包络等方式选择物理的碰撞类型。基于模型纹理的物理仿真方法会在模型面数较多时出现计算复杂度高的问题，从而引起穿模，而基于矩形包络、球包络等的物理仿真方法虽然可以避免模型之间产生穿模现象，但是模型形状的简化会使工件之间的堆叠不能反映真实场景中的碰撞堆叠效果。因此，本文首先利用高精度的三维扫描仪，拍摄工件多个角度的三维点云并进行配准，得到工件的完整点云；接着采用贪婪投影三角法进行曲面重建，得到复杂工业零件的精确模型，如图1（a）所示。为了尽可能减少模型面数从而减少仿真计算量，并保证物理碰撞尽可能与真实场景相似，本文对每一个特定的工业零件，实心化对物理碰撞不会产生影响的局部区域，而对于产生碰撞的区域，使用相对简单的形状进行包络拟合，如图1（b）所示。在图1 中，本文采用的4 种工件从上到下依次为轴承座1、轴承座2、连杆和榔头。

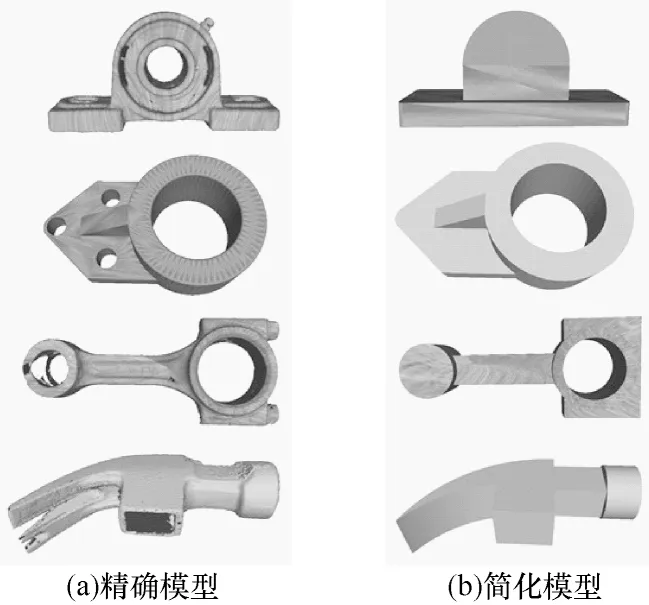
图1 精确模型与简化模型Fig.1 Exact model and simplified model

1.2 基于物理仿真的数据集生成

本文数据集生成的步骤如下：1）将多个简化的工件模型预设置随机位姿并置于环境上方；2）工件依靠重力下落，基于模型纹理产生碰撞散乱堆叠在相机视野下，然后渲染得到每个工件的掩码与之后生成的深度图对应得到点云的类别标签；3）在获取堆叠工件位姿后，在Bullet 中用重建的精确点云模型代替简化模型，渲染得到深度图，进而获得散乱场景的点云，如图2 所示。这样就可以使得仿真生成的散乱堆叠工件的点云以及工件之间的碰撞效果和真实场景尽可能相似，防止由于模型面数过多造成穿模问题。由于Blender 中的工件在世界坐标系下的坐标变换为因此需要将其转换到相机坐标系下，已知相机在世界坐标系下的坐标变换为则工件在相机坐标系下的六维位姿为：

图2 散乱场景的点云仿真Fig.2 Simulation of point clouds in scattered scene

2 基于深度学习的点云位姿估计方法

直接将学习得到的原始点云特征输入全连接层进行训练可以达到很好的分类效果［17-18］，但对于六维位姿估计效果并不理想，因为训练得到的全局特征和每个点的局部特征更多的是表现该工件的类别特征，而用于估计六维位姿的局部表面特征和几何特征并未进行有效提取，仅依靠神经网络本身参数的调整和训练效果较差。另外，神经网络的数据输入维度需要保持一致，而从场景分割得到的单个点云的点数是不确定的，为了使其能够输入网络，需要采样成固定点数，这会使得工件点云变得稀疏，从而损失一定的特征。近年来研究人员提出了许多成熟的处理二维图像的深度学习方法，因此本文将三维点云映射到二维平面，生成深度特征图和法线特征图并提取位姿特征，不仅保证了网络输入维度一致，而且大幅提高了基于点云的位姿估计准确率。

2.1 点云二维深度特征生成

在位姿估计前，本文利用ASIS 方法［22］对散乱场景的点云进行分割预处理。对于每一个分割后的单个工件点云，计算其xyz坐标的平均值xm、ym、zm，记为点云的中心，并将点云中心移动到相机坐标系原点，如图3中A 所示，记为tO=(-xm，-ym，-zm)T并得到：

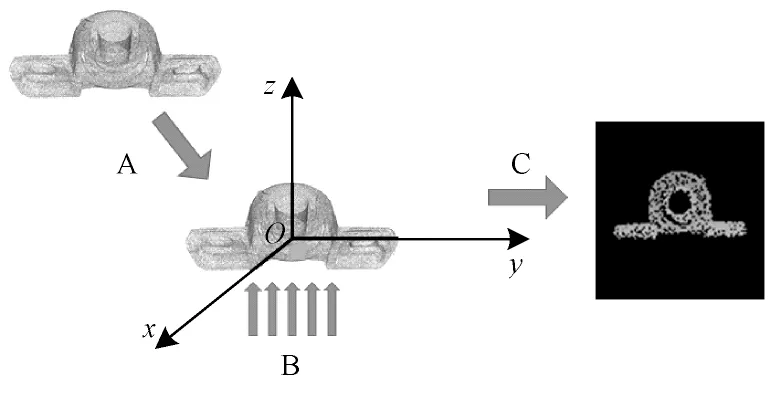
图3 点云二维特征生成Fig.3 2D feature generation of point clouds

将点云平移到坐标原点附近可以有效减小图像尺寸，使样本点所占二维图像的比例尽可能大，增加图像特征的显著度。点云到二维图像的具体映射方法为：1）设定分辨率及宽度方向的像素个数，按照图像宽高尺寸的比例设定高度方向的像素个数；2）将点投影到图像中时，会出现一个像素中存在多个点的情况，此时仅保留z值最小的点，该点离观测视野最近，识别度最高；3）由于二维图像是单通道的灰度图，因此得到点像素的灰度值为：

由于设定的分辨率不同，因此每个像素包含点的数量也会发生变化，而二维图像的特征也会有所差别。图4 给出了在不同分辨率下工件仅通过二维深度特征进行位姿估计的准确率。可以看出，分辨率从起始到80 像素×80 像素时，位姿估计的准确率提升得很快，再提高分辨率时，位姿估计准确率的提升开始减缓，并且约在100 像素×100 像素时达到最大，此时进一步提高分辨率，准确率开始缓慢下降。由于分辨率过大或者过小都会造成点云二维特征不够明显，因此在实验阶段，本文将特征图的分辨率设置为峰顶处的100 像素×100 像素。同时，本文工件的尺寸设置为10～20 cm，如果物体尺寸大于实验采用的工件尺寸，可以适当提高分辨率，反之亦然。笔者认为应谨慎降低特征图的分辨率，因为从实验结果可以看出，过大的分辨率对实验结果的影响远小于过小的分辨率。

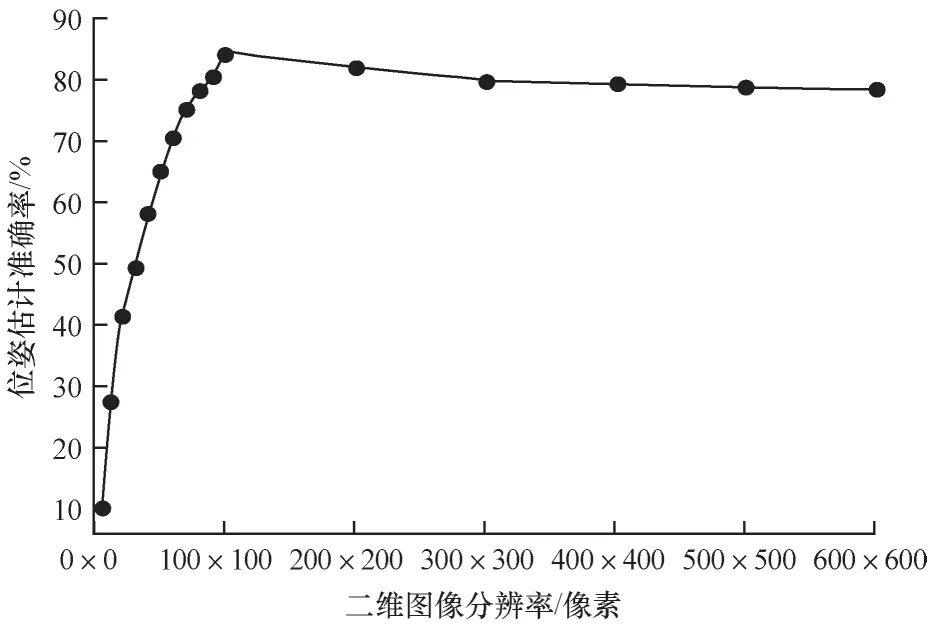
图4 不同分辨率下位姿估计的准确率Fig.4 Accuracy of pose estimation at different resolutions

2.2 点云二维法线特征生成

点云生成的二维深度特征能够有效提取出工件的几何特征，但是一些不同的工件或者一个工件的不同局部投影到二维平面，有可能呈现类似的形状，即使深度不一致，也会影响最终的估计结果。如图5（a）、图5（b）所示，轴承座2 的正反面投影到二维平面会产生上述问题。而点云法线作为点云的一种重要的几何属性，已广泛应用于特征点检测、三维重建、薄板正反面区分等场景。传统位姿估计算法的点对特征［14］就是运用两点的法线特征构建特征算子，而近年来许多基于点云分类分割的深度学习研究［17-18］也将点云的表面法线作为点云的额外信息输入网络进行训练，经过实验证明，分割准确度有了明显提升。因此，本文类比二维深度特征图的生成方式生成点云的二维法线特征图，用于增加二维特征的区分度，即使不同位姿样本的二维深度图相似，最终的位姿估计结果也不会产生误匹配的情况。

在将点云投影到二维平面生成的深度特征图前，利用Open3D 库计算点云的法线，这样二维深度特征图中任意点像素都会包含这个点的深度值及其法线。将各点的三维法线特征和深度值分离，即可得到二维法线特征图。本文思想是将法线特征和深度特征分成两条支路，各自学习对应的特征，最终将网络学到的特征信息进行融合输出六维位姿。在二维法线特征图生成的过程中存在两方面的问题。一方面，通过上述方法计算出的法线并没有经过全局定向，这会极大地影响模型对工件位姿的训练。本文将所有法线的方向统一至与z轴负方向呈小于90°的夹角，解决了全局定向的问题，将二维法线特征图中计算得到的法线以及该像素缓存的三维点还原成空间点云，可以看到法线的取向是统一的，如图5（c）、图5（d）所示。另一方面，在二维法线特征计算的过程中引入了分割后的噪声，特别是在工件的边缘位置处，法线的估计会因为噪声产生很大的误差，因此本文在实验部分将噪声对位姿估计结果的影响进行实验验证。

图5 轴承座2 的正反面及其点云法线Fig.5 Front and back sides and their point cloud normals of bearing pedestal 2

2.3 特征融合网络

本文提出的特征融合网络框架如图6 所示。特征融合网络主要包括：1）二维深度特征提取，将点云映射为二维深度特征图，经过预处理后输入resnet50 预训练模型进行预训练，每个样本得到2 048 维特征，经过多个全连接层后得到256 维特征；2）二维法线特征提取，投影生成二维法线特征图后，经过多个卷积层得到通道数为1 024的特征图，通过多个卷积核为2×2 与5×5的卷积层得到通道数为1 024 的特征图，并经过最大池化处理平铺生成1 024 维的全连接层，之后分为2 个支路经过全连接层分别得到256 维特征，该网络采用Relu激活函数；3）将二维深度特征提取过程中得到的特征分别于二维法线特征提取过程中的两条支路进行特征拼接，经过多个全连接层后，两支路分别得到三维特征和四维特征，代表工件位姿的xyz值以及表示旋转的四元数，将四元数转换为旋转矩阵后即可得到4×4 的六维位姿矩阵。

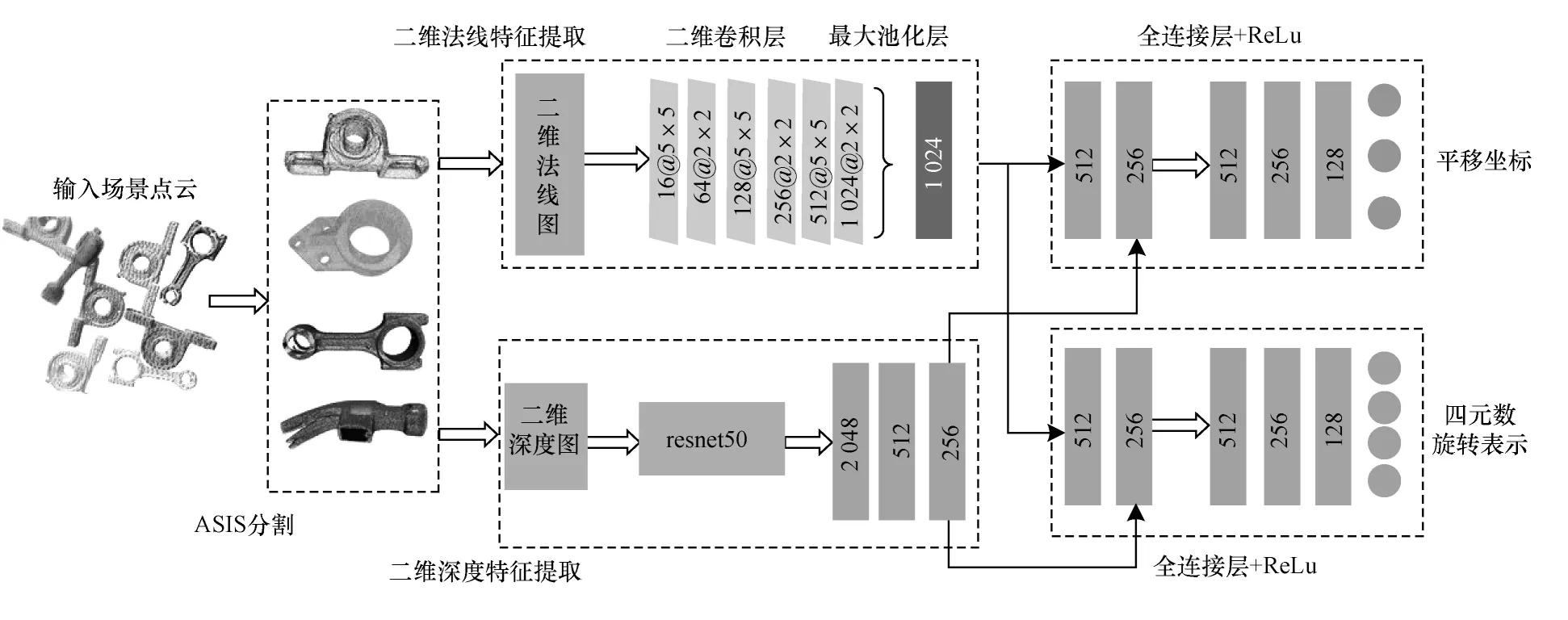
图6 特征融合网络框架Fig.6 Framework of feature fusion network

2.4 损失函数

在基于深度学习的位姿回归中，常见的一种损失函数是计算使用真实位姿回归得到的点云和使用估计位姿回归得到的点云中对应点距离的平均值［5］，记为CPLoss，计算公式如下：

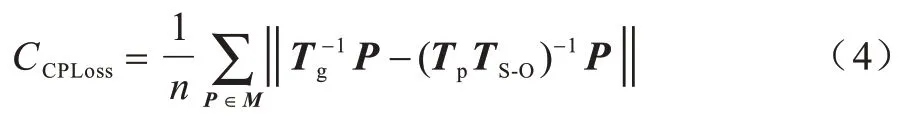
其中：M表示已事先采样的模型点云；n表示采样点个数；Tg、Tp分别表示标签位姿和估计位姿。需要注意的是，网络估计的位姿是分割后的局部点云到相机坐标系原点的模板点云的变换位姿，而计算损失函数使用模型点云到场景点云中的变换位姿，因此需要对变换矩阵求逆。

CPLoss 损失函数可以有效地表示估计位姿回归的准确程度，但是对于一些对称物体而言，多个位姿可能对应同一个正确的姿态，从而使网络回归到另一个可代替的位姿上，造成损失函数给出不一致的训练信号。针对这一问题，本文采用类似于迭代最近点（Iterative Closest Point，ICP）算法的损失函数ICPLoss，计算估计位姿回归得到的点云中的每一个点离真实位姿回归得到点云的最近点的距离并取平均值，计算公式如下：

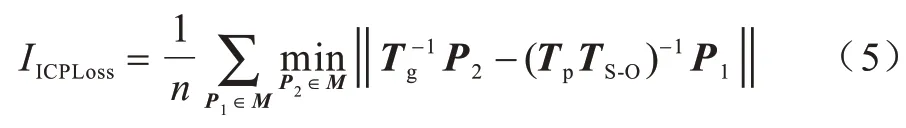
3 实验验证

在进行位姿估计前，需要对获取的场景点云进行实例分割。本文采用ASIS［21］实例分割算法，根据同类实例点的特征向量相近、不同类实例点的特征向量相差较远的原则进行实例分割。因此，工件在无遮挡堆叠的情况下，分割效果是非常理想的，而由于本文在抓取过程中每次仅对场景中的一个实例进行位姿估计，对于遮挡堆叠严重的场景点云，将最上层实例分割分数最为理想的工件作为待抓取工件，可以避免遮挡堆叠带来的分割误差。图7（a）是真实场景的散乱堆叠工件，图7（b）、图7（c）是真实场景点云的两个分割实例。图8 是针对图7（a）的真实场景位姿估计实例，通过网络估计工件位姿并利用ICP 进行位姿细化得到可抓取工件的精确六维位姿，接着通过机器人进行工件的抓取，重复以上过程即是一次完整的散乱工件抓取的流程。图8（a）～图8（h）显示了将模型点云基于估计得到的精确六维位姿变换回场景中，可以看出模型点云和场景中的目标点云基本重合。

图7 真实场景的点云分割实例Fig.7 Examples of point clouds segmentation of real scene

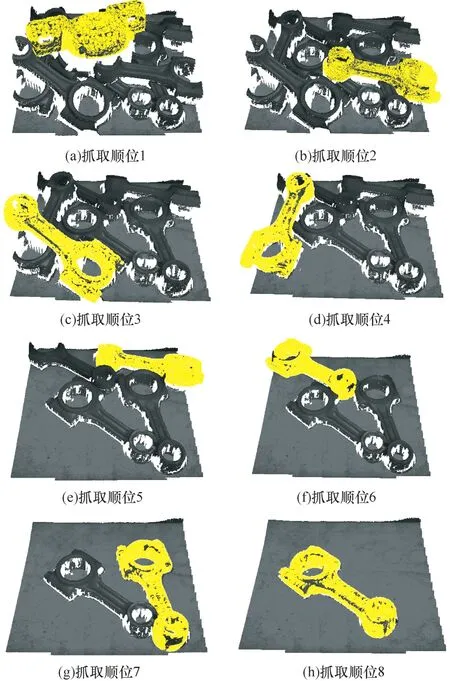
图8 真实场景的位姿估计实例Fig.8 Examples of pose estimation of real scene

3.1 实验参数设置

本文针对4 种不同的工业零件进行六维位姿估计实验。在数据集中，每类工件都有8 000 个分割后的点云样本作为训练集，2 000 个样本作为测试集，每个样本包含2 048 个采样点。对于非对称工件，由于本文采用的工件尺寸为10～20 cm，因此将CPLoss 小于工件尺寸最大直径的1/10视为位姿估计正确。对于对称工件，判别标准是ICPLoss 的大小，经过实验评估，轴承座1和连杆的回归损失ICPLoss 分别小于2 mm 和1.4 mm时，可视为位姿回归正确。如果训练的工件尺寸和本文相差很大，则需重新选定合理的阈值。

3.2 与传统位姿估计方法的性能对比

将本文方法与粗配准+ICP、PPF、深度+ICP 方法进行对比，如表1 所示，其中最优指标值用加粗字体标示。可以看出，使用深度特征和法线特征相融合的位姿估计方法比仅使用深度特征的位姿估计方法具有更高的估计准确率。对于对称工件而言，即轴承座1 和连杆，PPF 和本文方法均能达到很高的估计准确率，而粗配准+ICP 方法效果较差；对于非对称工件而言，即轴承座2 和榔头，本文方法在准确率上远超粗配准+ICP 和PPF 方法。

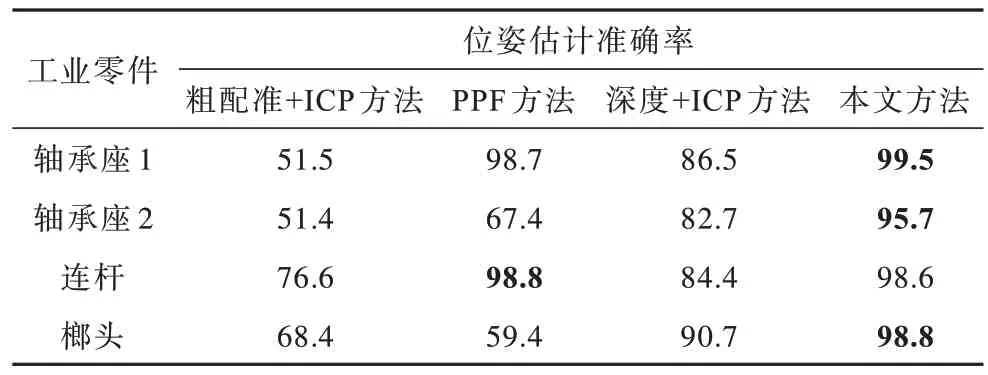
表1 工业零件在不同方法下的位姿估计准确率Table 1 Accuracy of pose estimation of industrial parts with different methods %

图9 给出了PPF 匹配错误的两种情况，可以看出榔头正反面是两个类似的平面，而当分割后的输入点云是类似于图中这样的局部平面时，PPF 或者粗配准+ICP 方法很可能会将其匹配到工件的一个类似平面上，方向和位置完全错误。由此得出，传统方法是通过计算特征点对的方式进行匹配的，它们没有获取输入点云的局部外形特征和几何特征，在有相似特征的情况下很容易匹配错误，而本文方法没有出现这方面的问题。

图9 PPF 错误匹配样本Fig.9 PPF error matching samples

表2 给出了3 种方法的平均位姿估计时间对比结果。本文所有涉及ICP 位姿细化的地方，均将终止条件定为两次迭代的结果之差小于10-6m。可以看出，本文方法非常高效，估计一次的时间远少于粗配准+ICP方法的时间，也略快于PPF 方法。同时，对于增加的法线特征支路，其浮点运算量为2.1×108，而深度特征支路resnet50 的浮点运算量为3.8×109，约为前者的1.8 倍。可见，特征融合网络相比单特征网络运算复杂度和位姿估计时间并未明显增加，这是因为整个网络的运算复杂度主要由深度特征支路以及之后的全连接层决定。

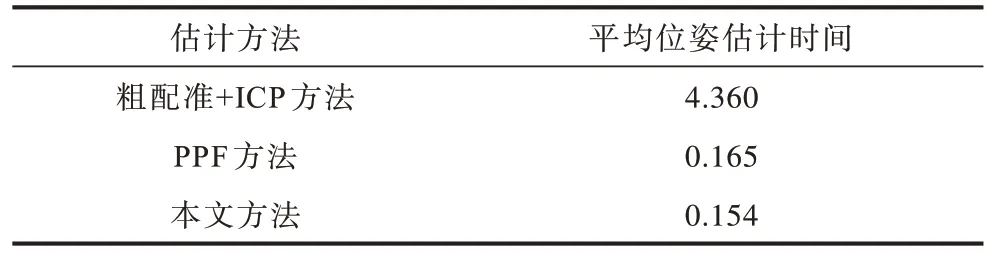
表2 3 种方法的平均位姿估计时间对比Table 2 Comparison of the average pose estimation time of three methods s

3.3 其他因素对估计结果的影响

由于真实场景中分割得到的单个点云的点个数是不确定的，而本文训练采用的数据集中每个样本都是2 048 个点，因此本文将各种采样点数的点云分别输入训练好的模型进行位姿预测并统计各种方法在不同采样点数下的位姿估计准确率。图10 给出了采用3 种方法的榔头工件位姿估计准确率对比结果。可以看出，在不同采样点数下，本文方法在估计准确率上未有明显变化，说明本文训练的模型可以针对不同点数的点云进行位姿估计，而其他两种方法在点数变少时准确率出现递减的情况。

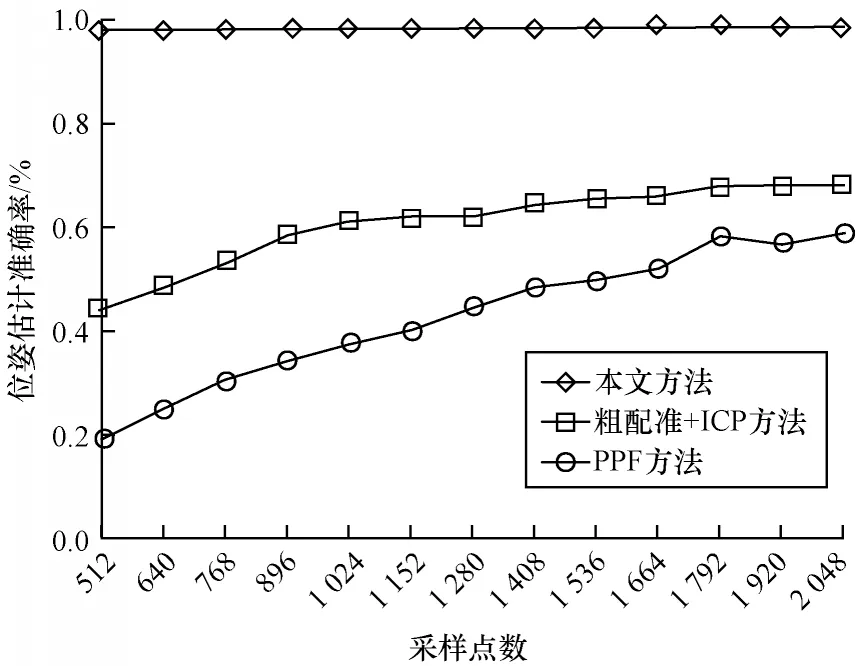
图10 不同采样点数下位姿估计准确率的对比Fig.10 Comparison of accuracy of pose estimation under different sampling points

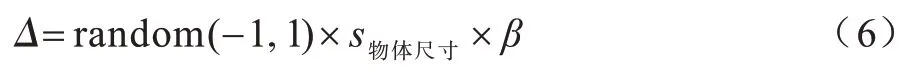
针对噪声对法线特征图的影响，本文对测试数据的每一个点加入随机噪声Δ：其中：β是比例系数，为使噪声的影响更加显著，本文将其设定为0.05。表3 给出了本文方法在无噪声的测试集、添加噪声样本的测试集以及添加噪声样本的训练集上进行训练后得到的测试结果。可以看出，噪声对位姿估计准确率的影响较小，并且将一些带有噪声的样本加入训练集后可以避免该影响。因此，经过实验证实，本文方法对噪声的鲁棒性较强。

表3 噪声对本文方法位姿估计准确率的影响Table 3 The effect of noise on the accuracy of the proposed pose estimation method %

4 结束语

本文提出一种基于深度学习的点云位姿估计方法，将分割后的单个点云投影到二维平面，生成深度特征图和法线特征图，用于提取点云的局部表面特征和几何特征，从而估计出准确的六维位姿。在仿真数据集和真实数据集上的实验结果验证了该方法的有效性，并表明其在一定程度上解决了传统位姿估计方法计算量大且鲁棒性差的问题。但由于本文方法是基于点云的实例分割，位姿估计的准确率依赖于实例分割的准确率，因此下一步将对分割和位姿估计进行有效结合形成端到端模型，在保证点云语义实例分割准确率的前提下进一步提升算法实时性。