面向异构架构的传递闭包并行算法

肖 汉，郭宝云，李彩林，周清雷

（1.郑州师范学院 信息科学与技术学院，郑州 450044；2.山东理工大学 建筑工程学院，山东 淄博 255000；3.郑州大学 信息工程学院，郑州 450001）

0 概述

传递闭包运算在图论、网络、计算机形式语言、语法分析以及开关电路中的故障检测和诊断领域都有着广泛的应用价值［1-2］。根据定义，关系传递闭包的计算是通过多次进行集合复合运算完成，运算量很大。同时，假如二元关系在某种情况下发生了改变，其中的某些序偶增加或减少，需要按照原方法将变化的二元关系重新计算来得到新关系的传递闭包，运算量则进一步增大［3-5］。这样容易造成大量数据无法实时处理，最终使整个应用系统处理的时间增加，因此如何快速有效地处理传递闭包问题成为了一个急需解决的问题［6-7］。

开展传统的利用CPU 集群的高性能计算是解决大规模科学计算问题的常用方法，然而集群的并行计算性能对于CPU 的更新换代的依赖性很大。由于CPU 芯片单位面积内的晶体管集成度越来越高，散热和能耗问题凸显，致使提升CPU 的速度放缓，发展陷入瓶颈［8-10］。为了更快地增强计算能力，计算机硬件设计的异构化的趋势越发明显［11-12］。由若干不同架构的CPU 处理器和协处理器共同工作，通用计算处理器与多个加速器设备互连构成的异构计算系统逐渐成为主流［13-14］。

开放式计算语言（Open Computing Language，OpenCL）是一个面向异构硬件平台的、免费的、开放的行业标准。遵循OpenCL 规范的不同架构的硬件，提供需要的编译和运行平台，就能够在OpenCL 平台上开发普适的应用系统，为多核CPU、CPU+GPU、DSP 和多GPU 等异构计算提供良好的研发平台［15-16］。

本文基于开放式计算语言平台，提出一种基于CPU+GPU 的高效传递闭包并行算法，并采用具有可移植性的OpenCL 架构来实现该算法。对在不同数据集下和不同体系结构下的算法和加速比进行分析。

1 相关研究

近年来，很多学者对传递闭包运算进行了研究。文献［17］用一阶有界传递闭包模糊逻辑来刻画模糊有穷自动机。文献［18］研究了稠密图条件下采用XHop 方法，对传递闭包进行高压缩比存储和有效查询的算法。文献［19］提出改进的传递闭包求解方法，并在传递闭包改进的求解方式基础上，设计了传递闭包的增量式更新方法。文献［20］证明只要函数在Jensen 的J层次结构的某个多项式级别中是统一可行的，则相对于函数参数的传递闭包，其在任意集上是安全递归的。文献［21］提出改进的Floyd-Warshall算法，其中最耗时的部分（描述程序循环中自相关的传递闭包）是通过依赖距离向量计算，减少了传递闭包计算时间。文献［22］基于程序依赖图的传递闭包，提出一种在瓦片内生成具有任意顺序循环的并行代码的方法。文献［23］使用循环嵌套依赖图的传递闭包来执行原始矩形瓦片的校正，生成并行无同步代码。文献［24］通过应用依赖图的传递闭包，提出生成Nussinov RNA 折叠算法的并行代码的加速因子。文献［25］通过MPI 并行化实现了Warshall 方法，进而快速求取了关系R的传递闭包R+。

文献［26］通过向量化方法将循环结构并行化，实现了传递闭包并行算法。文献［27］在二叉树并行计算模型上，实现了一种基于MPI 的传递闭包并行算法。文献［28］通过实现传递闭包并行算法，提高了在图形和高维数据中挖掘中心对象算法的收敛性。文献［29］利用MPI 提出了基于VLSI 的传递闭包并行算法。文献［30］通过合并Dijkstra 单源最短路径方法中的贪婪技术的特征和传递闭包属性来找到所有点对最短路径，并在MapReduce 平台上实现了ex-FTCD 算法。

综上所述，目前大部分研究工作是通过优化算法本身从而实现对传递闭包算法的快速计算，有些则利用传统的向量化和CPU 集群的MPI 并行计算方式设计传递闭包算法。但是，性能加速效果在这些相关研究中表现的均不明显。同时，算法研究和平台设计局限于单一类型，对于多算法和多平台的系统性能评估不多。本文将根据传递闭包算法特性和OpenCL 架构的特征，研究异构协同计算下的传递闭包并行算法，以及在多种计算平台上算法的性能移植。

2 传递闭包算法

2.1 OpenCL 异构编程模型

OpenCL 是一种面向开放的、通用并行编程的、跨平台的行业标准，软件开发人员可以方便地将CPU、GPU和其他各类计算设备接入系统计算［31-32］。OpenCL 标准是编程语言与编程框架的集合体，人们可以基于硬件抽象层API和面向数据的异构编程环境进行OpenCL系统的开发和优化应用。OpenCL 框架主要由OpenCL平台层、OpenCL 运行时环境和OpenCL 编译器3 个部分组成［33-35］。平台层允许用户收集可用的OpenCL 设备信息。开发者可以查询特定设备的详细资料，比如缓存大小、存储器结构、核心数量等。OpenCL Runtime提供了管理设备存储器、运行kernel、在设备与主机之间传输数据等一系列API［36-39］。OpenCL 编译器创建包含OpenCL kernel 的可执行程序，把kernel 编译成设备能够识别的代码。

2.2 算法定义

图的传递闭包可以采用布尔矩阵的平方法计算。首先假定A是一个m点有向图的m×m的布尔邻接矩阵，当且仅当有向图中从顶点i到顶点j之间有一条边时，矩阵元素aij为1。然后利用矩阵乘法对布尔矩阵的传递闭包A+求解［40-41］。设I是单位矩阵，大小为m×m的关系矩阵为B=A∪I。使矩阵B的第i行上的元素与矩阵B的第j列上的元素按顺序分别相乘再相加，得到新的关系矩阵B的第i行第j列的元素（关系矩阵B在不断更新），即B的定义如下：

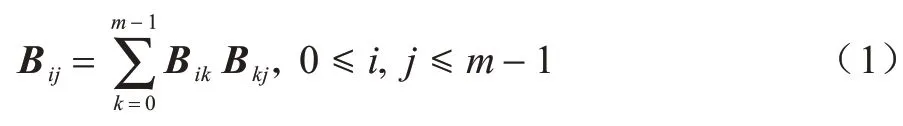
得到新的关系矩阵B重复上一步进行循环，即依次计算，即执行p＜logam次，得到布尔矩阵的传递闭包A+［42-44］。由此可知，算法的时间复杂性在最坏的情况下为O(m3logam)，当m非常大时，该算法运算将非常耗时［45］。

2.3 算法的并行特征分析

算法的可并行性高低与算法自身存在的数据依赖性有关。如果算法运算前后依赖性越强，则算法的可并行性就越低，反之，如果算法运算前后依赖性越弱，则算法的可并行性就越高，算法并行化后进行并行计算的性能就会越好。图1 所示是一个有向图的传递闭包算法的可并行性分析。

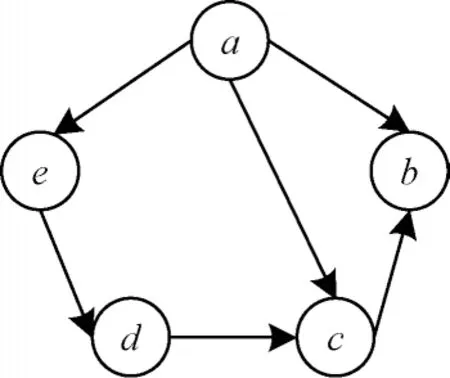
图1 有向图Fig.1 Directed graph

根据图1 的5 个顶点的有向图表示出布尔矩阵Aij，计算布尔矩阵Aij的闭包(Aij)÷过程如下：

在(Aij)÷的计算过程中可以发现，每一计算步骤中的任意一个元素的计算过程与其他元素计算互不影响，相互之间并没有依赖性。因此，可以在计算某一个元素值时，同时对其他元素值进行运算。结合OpenCL 的计算模型，将每个元素的计算过程放入工作项中，每个工作项计算得出相应元素的结果。若矩阵中每个元素计算结束，则本次计算结束，如果需要继续迭代，则再次重复以上过程。

3 传递闭包算法并行映射模型

3.1 并行算法

有向图布尔矩阵A的传递闭包可以利用B=(A+I)的自乘logam次得到。设定工作空间中的工作组和工作项排成m×m的二维阵列，即其坐标为(tx，ty)。每个工作组用数组as和数组bs存储矩阵B中相应子矩阵，Pvalue 保存的是每次子矩阵计算之后得到的值，数组C为每次计算完成之后最终数据。传递闭包并行算法描述如算法1 所示。

3.2 并行算法整体并行化思路

基于OpenCL 的传递闭包并行执行流程如图2所示。

图2 传递闭包并行算法实现流程Fig.2 Implementation procedure of transitive closure parallel algorithm

传递闭包并行算法执行过程如下：

1）在主机端根据对应的顶点数，初始化布尔矩阵A，并保存初始化后的布尔矩阵。

2）初始化OpenCL 平台。

3）创建上下文，并在目标设备上创建命令对象。为了协调内核计算，在上下文和计算设备之间利用clCreateCommandQueue 命令建立一个逻辑链接。

4）读入源程序文件，并创建和编译程序对象。根据上下文中的设备特性，利用运行时编译系统构建程序对象。

5）设置存储器对象和数据传输。在全局内存中创建buffer 存储器对象，然后将存储器访问任务加入到命令队列，最后通过clCreateBuffer 将布尔矩阵A、B从CPU 端隐式地传输到设备端的全局内存中。

6）建立内核对象。在指定的一个内核对象中将内核参数和内核函数通过clCreateKernel 封装进来。

7）设置需要传递的内核对象参数。

8）创建kernel 函数，调度kernel 执行。

9）循环调用kernel 函数对数据进行相应的处理，计算矩阵乘积大小。

10）将显存端完成运算任务后的结果复制到主机端内存，并且释放设备端显存空间，将最终的计算结果保存到对应的文件中。

3.3 算法的并行方案设计

在设计传递闭包并行算法时，矩阵乘法的并行计算采用了工作项分块的方法实现，计算原理如图3 所示。工作组中的每个工作项读取矩阵B中的一行和矩阵B中的一列，将行、列中对应元素相乘之后再相加，得到新矩阵B的对应位置元素值，即每个工作项对应计算新矩阵B中的一个元素。以上操作循环经过p＜logam次后得到有向图的传递闭包A+的形式矩阵。

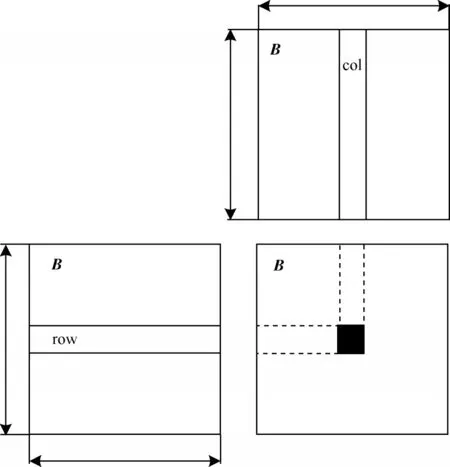
图3 传递闭包算法中的矩阵相乘Fig.3 Matrix multiplication in the transitive closure algorithm

按照相互之间无重叠的划分原则，整个矩阵B将被划分成若干个计算区域。计算区域可作为一个基本处理单位，由工作组处理。文中采用二维工作空间进行设计，从数据层面上看，每个工作组在x，y方向上的维度均为BLOCK_SIZE。工作空间在x、y方向上共有个工作组，每个工作组中执行了BLOCK_SIZE×BLOCK_SIZE 个工作项。

矩阵乘法中每一对元素间的乘-加计算由一个工作项负责。在内核函数中循环完成矩阵B第i行元素与矩阵B第j列元素的乘-加运算，并将乘-加的结果赋给Pvalue。在该kernel 函数中，矩阵B中的每一个元素从全局存储器中读取了m次，造成了时间上的大量延迟。

3.4 优化设计

GPU 全局存储器属于片下存储器，存储空间较大，但具有较高的访存延迟。而本地存储器是GPU片上的高速存储器，它的缓冲区驻留在物理GPU上。因此，本地存储器的访存延迟要远远低于全局存储器，大量工作项的并行执行能够在一定程度上掩盖全局存储器操作的延迟。

将矩阵相乘后得到的新矩阵B分解成小矩阵块，每一个工作组负责计算一个小矩阵块。若矩阵B的大小是m×m，则新矩阵B=B×B。假设m=b×b，将新矩阵B分为b×b个小的子矩阵bij，则每一个子矩阵bij的大小为b×b。2 个相乘的矩阵B同新矩阵B一样，划分为b×b个小的子矩阵bij，且每一个子矩阵bij的大小同为b×b，则传递闭包并行算法中采用分块矩阵乘法的定义为计算原理如图4 所示。

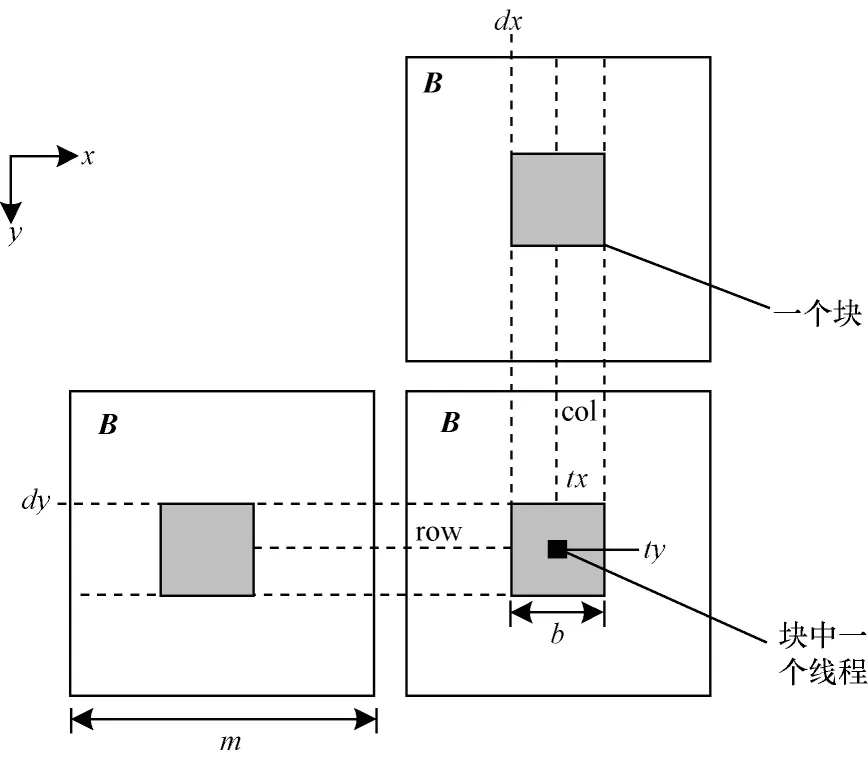
图4 传递闭包算法中的分块矩阵相乘Fig.4 Multiplication of block matrix in transitive closure algorithm

在传递闭包并行算法的分块矩阵乘法中，采用静态方式定义大小为BLOCK_SIZE×BLOCK_SIZE的本地存储器数组，用于存储矩阵B子块数据。

__local float as[BLOCK_SIZE][BLOCK_SIZE]

__local float bs[BLOCK_SIZE][BLOCK_SIZE]

为从全局存储器预取计算子矩阵到本地存储器，根据工作组的ID 和工作项的ID 确定B的计算子矩阵的位置，并将B中用于计算的2 个计算子矩阵分别预取至本地数组as和bs中。每个工作项负责计算一对元素的乘积和PPvalue+=as[ty][k]×bs[k][tx]。原来矩阵的一行或一列数据需要从全局存储器读取m次，现在只需要读取m/BBLOCK_SIZE次，这样在新矩阵B的计算过程中矩阵数据需要从全局存储器读取m×m次，优化后只需要读取m2/BBLOCK_SIZE次。因此，通过对GPU的存储带宽进行充分的利用，减少从全局存储器中重复读取数据。使用本地存储器不仅可以降低访问延迟以此提高访问速率，同时节约了对全局存储器的访问带宽。

4 实验测试与结果分析

本节将给出所描述的传递闭包方法的测试结果。由于单精度浮点运算针对现代计算机，特别是在GPU 上进行了高度优化，因此本文选择单精度数据类型实现算法。

4.1 测试环境和实验结果

实验软硬件平台如下：

1）硬件平台

平台1：CPU 为AMD Ryzen5 1600X 3.6 GHz（六核心），24.0 GB 的系统内存。GPU 型号是NVIDIA GeForce GTX 1070，CUDA 核心1 920 颗，1 506 MHz的核心频率，1 683 MHz 的流处理器频率，8 GB GDDR5 的显存，256 bit 的显存位宽，256 Gb/s 的显存带宽，显存存取速率为8 Gb/s。

平台2：CPU 为AMD Ryzen5 1600X 3.6 GHz（六核心），24.0 GB 的系统内存。GPU 型号是AMD Radeon RX 570，其中，计算单元32 组，每组计算单元具有64 个处理单元，总计2 048 颗流处理单元，1 168 MHz 的核心频率，256 bit 的显存位宽，8 GB GDDR5 显存。

2）软件平台：操作系统采用微软Windows 8.1 64位；集成开发环境为微软Visual Studio 2017；系统编译环境为CUDA Toolkit 8.0，OpenCL 1.2 标准被支持。

有向图的顶点集合大小n分别取为20、40、50、70、200、300、500、1 024，作为rand()随机数函数的随机数种子分别生成一组随机数，构成布尔矩阵A。根据本文的传递闭包算法的描述，基于OpenMP 平台和基于CUDA 平台的传递闭包并行算法均在文中实现。

传递闭包算法运行在基于OpenMP系统、基于CUDA系统、基于AMD GPU 的OpenCL系统和基于NVIDIA GPU 的OpenCL系统的上处理时间，如表1所示。处理时间包括传递闭包算法的所有处理步骤。在OpenCL 中实现GPU 并行算法时，必须执行额外的步骤，如内核创建（读取、创建和构建最终内核对象）、主机内存和GPU 全局存储器之间的数据传输以及数据结构初始化。

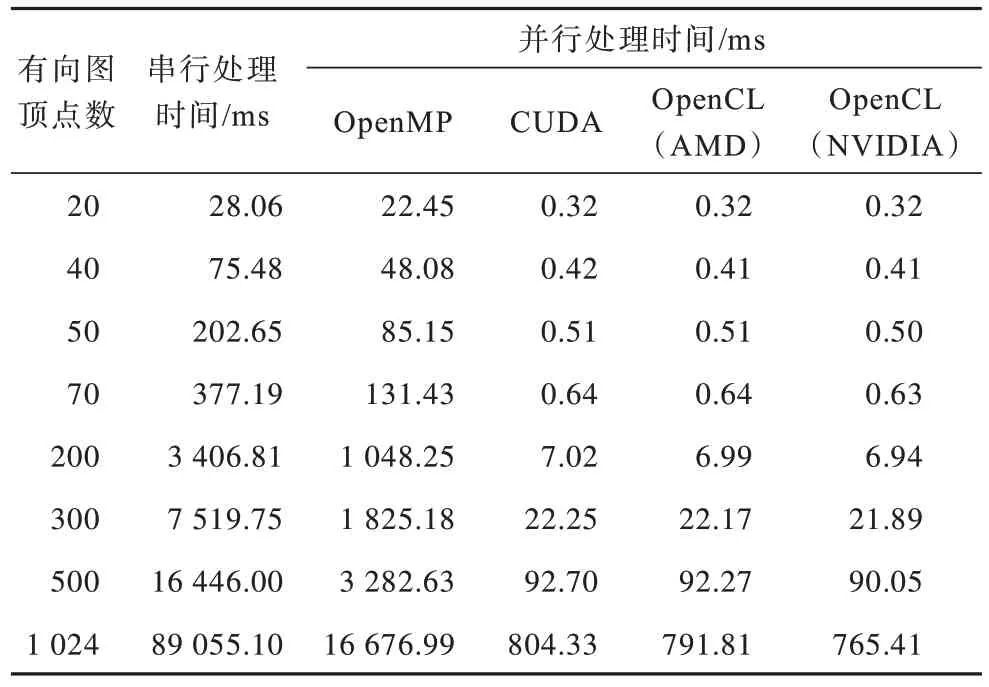
表1 传递闭包算法执行时间Table 1 Execution time of transitive closure algorithm

用加速比作为加速效果的衡量标准，可以直观地验证各种架构下并行算法的效率，其定义如下：

CPU 串行算法执行时间与并行算法执行时间的比值即为加速比：

其中：Tserial是在CPU 上单个线程的顺序运算时间；Tparallel是在多核CPU 或CPU+GPU 上多线程实现的并行运算时间。

相对加速比1基于OpenMP 的并行算法运算时间与基于NVIDIA GPU 的OpenCL 并行算法运算时间的比值：

其中：Tparallel-OpenMP是在多核CPU 上多线程的并行运算时间；Tparallel-NOpenCL是在NVIDIA GPU 上OpenCL 的并行运算时间。

相对加速比2基于NVIDIA GPU 平台的CUDA 并行算法运算时间与基于NVIDIA GPU 平台的OpenCL 并行算法运算时间的比值：

其中：Tparallel-CUDA是在CUDA 上的并行执行时间；Tparallel-NOpenCL是在NVIDIA GPU 上OpenCL 并行实现的并行执行时间。Tparallel-CUDA和Tparallel-NOpenCL定义如下：

其中：Tkernel为OpenCL 内核在CPU 和GPU 上总的执行时间；Tovehead为在CPU 和GPU 上数据传输时间开销的总和；Tother为数据结构初始化等操作总的运行时间。

为了更好地对应用系统速度进行客观评价，采用加速比指标来反映在一定的计算架构下的并行算法相较串行算法的效率提升幅度。使用相对加速比1 指标来反映基于NVIDIA GPU 的OpenCL 并行算法相比基于多核CPU 的OpenMP 并行算法的效率提升情况，相对加速比2 指标则反映出基于NVIDIA GPU 的OpenCL 并行算法相比基于GPU 的CUDA 并行算法的效率提升情况，如表2 所示。

表2 传递闭包并行算法性能对比Table 2 Performance comparison of transitive closure parallel algorithm

4.2 实验数据分析

4.2.1 系统性能瓶颈分析

在存储器读写操作时，需要邻接矩阵数据的m×m×m次存储器读取，有向图的传递闭包矩阵数据的m×m次存储器写入操作。设一个m=200 点的有向图，每个像素值分配存储空间大小是4 Byte，所以，存储器存取数据总量约为0.032 GB，除以kernel 实际执行的时间0.000 257 s，得到的带宽数值是约124.51 GB/s，这已经接近GeForce Tesla C2075 显示存储器的150.34 GB/s 带宽。因此，可以很明显地看出，基于OpenCL 架构的传递闭包并行算法的效率受限于全局存储器带宽。

从表2 可以看出，基于CPU+GPU 的算法加速效果明显，但GPU 并行算法的加速比随着有向图顶点数的增加呈现缓慢下降的趋势。主要原因是在OpenCL 并行算法操作中，CPU 负责读取和输出图的邻接矩阵数据，而这一过程并没有加速。随着被处理邻接矩阵规模的增加，读取和输出邻接矩阵数据所花费的时间也在增加。因此，OpenCL 架构下的传递闭包并行算法的性能瓶颈是显存带宽和主存与显存之间数据传输的带宽。

4.2.2 传递闭包并行算法性能分析

不同并行计算平台下的传递闭包并行算法加速比对比曲线如图5 所示。在多核CPU 平台上，传递闭包算法的运算速度得到加速。然而，限于核心数，系统的加速比相对较小且变化不大，但由于GPU 具有较丰富的计算资源，在CUDA 架构和OpenCL 架构下的传递闭包算法就可以拥有足够的工作项来进行大量数据的并行处理。1 920 个处理单元通过时间分割机制分配到一定数量的工作项，加速比得到较大提高且增幅明显。通过表2 分析，在对计算密集型特征明显的大规模数据集计算时，GPU系统运算时间有小量增幅，体现了GPU 用于计算密集型的任务运算不如CPU 敏感，显现出GPU 强大的运算能力。

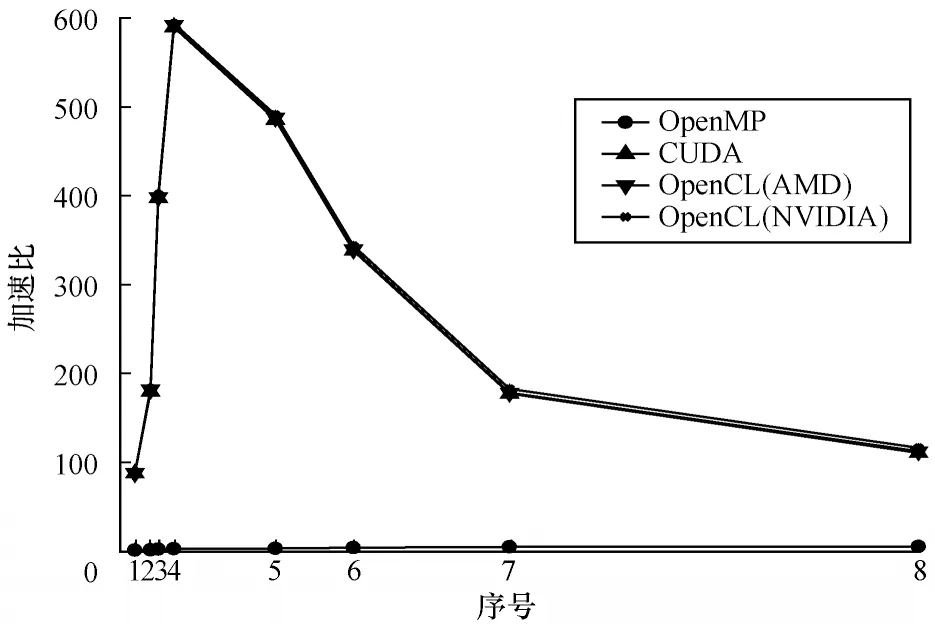
图5 传递闭包并行算法的加速比对比Fig.5 Comparison of acceleration ratios of transitive closure parallel algorithm

由图5 可知，随着布尔矩阵规模的增加，GPU 加速下的加速比曲线斜率急剧变大，曲线变得十分陡峭。加速比呈现出快速增加的趋势，比较明显地体现出并行处理的性能提升效果。然而当布尔矩阵大小超过70×70 继续增大时，曲线呈现出一种下降趋势。虽然随着布尔矩阵规模的增大，工作空间中包含的工作组数也随之增多，系统中可同时执行更多的子矩阵，对于提高访问全局存储器和本地存储器的效率有益，也越容易隐藏存储器延时，但是布尔矩阵规模的增大，主机端和设备端存储器之间交互数据的时间成本变大，较大程度地抵消了GPU 并行计算的优势，导致GPU系统加速性能下降，整体系统性能受到制约。

4.2.3 传递闭包并行算法跨平台性分析

可移植性不但要求源码能够在不同的平台上成功地编译、运行，而且还需要算法应当有相当的性能。运算结果表明，在CUDA 架构下的传递闭包并行算法受到单一硬件平台的限制，而基于OpenCL 的传递闭包并行算法则在多种硬件平台上获得了较好的可移植性和兼容性，其最大加速比为593.14 倍，如图6 所示。

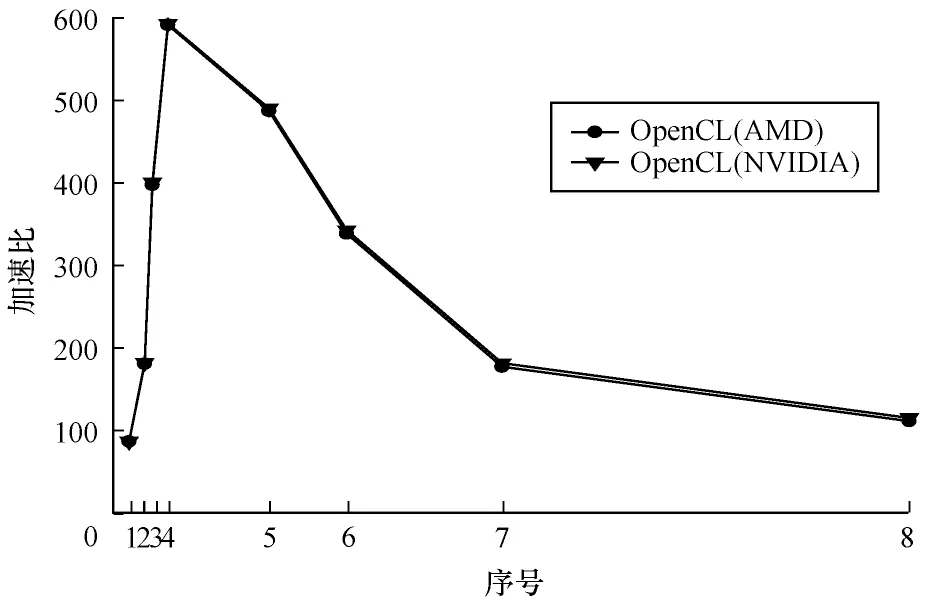
图6 OpenCL 加速比趋势Fig.6 OpenCL acceleration ratio trend

由于采用离线编译内核读写数据文件的OpenCL加速的传递闭包并行算法，相比在线编译内核读写数据文件的CUDA 加速的传递闭包并行算法减少了应用初始化时间。在同等数据集规模下，基于OpenCL 的传递闭包并行算法的运算耗时更少，与CUDA 计算平台上的算法性能相比略有提升，最大获得了1.05 倍加速比。而OpenCL 加速的传递闭包并行算法性能较之OpenMP 计算平台下的算法性能则有很大的提高，加速比最大获得了208.62 倍，如图7 所示。

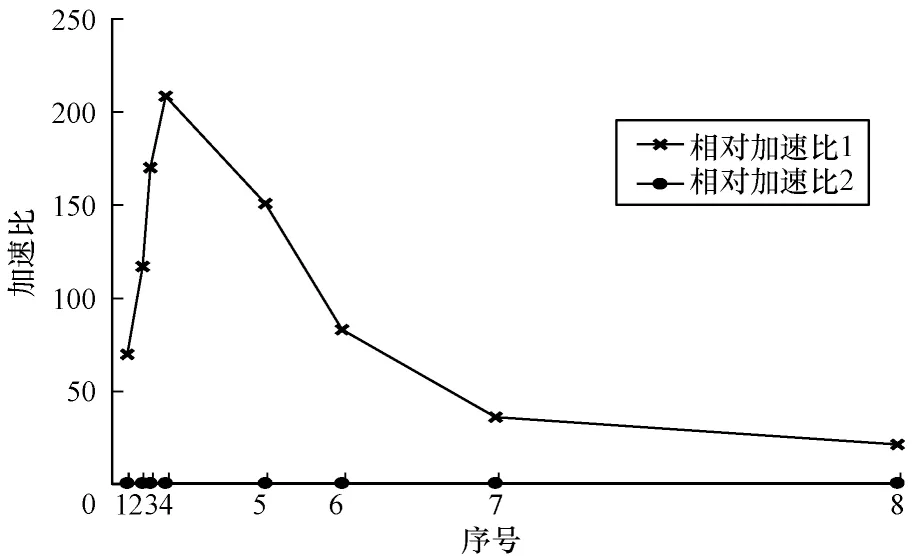
图7 相对加速比趋势Fig.7 Relative acceleration ratio trend

5 结束语

在许多应用系统中传递闭包是必要的基本部件，且为系统中较为耗时的部分，而矩阵乘对整个系统实时性能则有较大影响。本文针对传递闭包算法串行性能低下的不足，提出适合于OpenCL 架构的计算模式，并设计实现了传递闭包GPU 并行算法。实验结果表明，基于OpenCL 架构的传递闭包并行算法的性能相比CPU 串行算法、基于CPU 的OpenMP 并行算法和基于GPU 的CUDA 并行算法，分别取得了593.14 倍、208.62 倍和1.05 倍的加速比。在算法的GPU 实现过程中配置适当的内核参数和合理的分块参数，能有效提高处理效率，且实现同等计算量的GPU 相比CPU，性价比更高。因此，采用本文GPU异构计算模式对大规模数据运算且系统实时性要求较高的应用，将是一条新的思路。