自动涂胶安装类设备稳定性测试方法研究
2021-08-20尹斐张梅梅
尹斐 张梅梅
(一汽-大众汽车有限公司,长春130011)
1 前言
自动涂胶安装类设备针对的零件(如风挡、全景天窗等)对装配后的装配质量有较高的要求。装配质量受环境、零件状态、车身状态、设备状态、机械化输送等多个环节影响,这些环节的波动都将造成最后装配质量产生一定波动。其中匹配质量的控制是该类设备的难点,围绕提高匹配质量存在大量的调试优化工作,但保证设备装配的稳定性是调试优化的前提。当前,业内主要通过工业机器人与视觉系统相结合的技术形式实现装配过程,实现了设备柔性化生产,同时也造成了其无法通过传统的机械检具来验证其精度及稳定性的现状。本研究将阐述确定该类设备匹配质量稳定性能力的方法及相应的测试评价方法,以衡量设备能否满足工艺要求。
2 设备运行基本原理
自动涂胶安装类设备自动化程度高,其从上件、涂胶、安装、检测全过程都实现了无人化的自动运行。该类设备一般由上料站、移栽机构、对中台、涂胶系统、安装机器人、视觉机器人、视觉系统组成。
a.上料站及移栽机构可存储零件并将零件自动搬运至对中台,而对中台消除了零件的定位及物流器具定位偏差。涂胶系统负责涂胶过程时胶的输出和控制,安装机器人负责抓取对中台上定位的零件,并与涂胶系统配合实现零件涂胶,获取到视觉系统的引导值后,将零件按压在车身顶盖钣金上,使零件通过胶固定在车身顶盖钣金上。
视觉机器人搭载视觉系统对车身特征区域进行捕捉(图1)[2],计算出车身与零位状态相比的变化值,并将变化值发送给安装机器人,对安装动作进行引导。零位状态是指在调试时,选用调试车身进行初始模板设定的状态,包含特征点拟合的车身顶盖钣金中心点及安装机器人安装动作在世界坐标系下的坐标值。自动运行时,安装过程实际是将当前的车身状态与初始状态对比,根据特征点位置的变化拟合出车身顶盖钣金中心点的变化值,安装机器人以零件中心点为参照点将该变化值补偿至安装动作中,从而引导安装。

图1 视觉引导示意
3 设备关键路径及能力模型
3.1 设备运行关键路径及分析
虽然设备运行整个过程流较复杂,但实际最终匹配质量只受关键路径的影响,设备关键路径如图2所示。
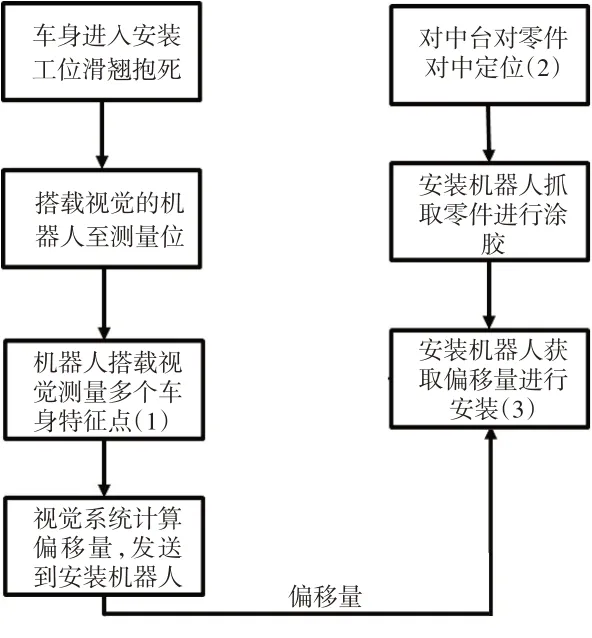
图2 设备关键路径
引起最终零件整体匹配波动的主要来源如下。
a.视觉引导偏差,即视觉机器人到设定拍照位置进行测量时,由于机器人本身的精度和视觉拍照精度导致特征点的位置坐标识别出现偏差,进而导致顶盖钣金中心点出现一定拟合偏差;
b.对中定位偏差,即对中台对零件进行对中操作时,电机驱动皮带对零件进行夹紧对中,由于电机及传动机构的精度,使零件在对中台的定位出现一定偏差,同时机器人本身精度将导致抓取位置相对波动,这些都导致机器人在对中台上抓取零件时,零件在机器人夹具上的定位产生偏差;
c.安装定位偏差,即在最后一个步骤,安装机器人将零件最终安装在车身上时,由于机器人的精度将导致安装动作出现一定波动,导致零件安装在车身上产生一定量偏差。
设备的匹配质量稳定性将由视觉机器人、视觉系统、对中台、安装机器人四个关键部件控制。
3.2 设备能力计算模型
虽然涂胶类玻璃零件不同车型形状存在一定差别,但大体比较接近,一般较平整,可将边框近似看成在一个平面上,且边框的形状与等腰梯形接近。同样,由于车身顶盖钣金边框与之匹配,形状为与玻璃零件匹配的形状。即可视零件边框与顶盖钣金边框视为一个平面上的类等腰梯形形状,且顶盖钣金边框为零件边框的等比例放大。
3.2.1 视觉定位能力计算模型
对于视觉引导能力,设备获取的各特征点拟合成顶盖钣金中心点,由于视觉机器人精度与视觉精度将导致特征点拾取的坐标值出现偏差,而导致拟合的车顶钣金中心点与实际会存在一定差别。
各特征点坐标值为机器人搭载视觉拍照获得,则各视觉特征点的精度为机器人的精度与视觉精度之和:
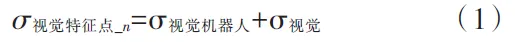
式中,n=1~6。
视觉定位原理为将各特征点拟合成顶盖钣金中心点,安装机器人按照中心点的偏移量进行位置补偿,实现定位。则整体的视觉定位的重复精度,实际即为拟合的顶盖钣金中心点的重复精度。而中心点的重复精度将由各视觉特征点重复精度决定,经推导可得出两者为相等关系。证明如下,假设存在两个定位点A1、A2,两点的重复精度都为r,则两点在精度范围内的空间实际坐标为(xi+Δxi,yi+Δyi,zi+Δzi),其中Δxi,Δyi,Δzi(i=1或2)为距离理想位置的偏差值。如图4所示,点a是A1A2连线内任意一点,令A1a/A1A2为k,可得a点空间坐标为(x1+Δx1+k(x2+Δx2-x1-Δx1),y1+Δy1+k(y2+Δy2-y1-Δy1),z1+Δz1+k(z2+Δz2-z1-Δz1)),可推导a点距离理想位置的偏差值Δxa2+Δya2+Δza2=[(1-k)Δx1+kΔx2]2+[(1-k)Δy1+kΔy2]2+[(1-k)Δz1+kΔz2]2≤r2。而假设线段在极限位置平移时,a点也能形成半径为r的包络球面,所以a点的重复精度也为r。

图3 端点波动线段示意
如图4所示,拟合的车身顶盖中心点Oc必然能经过两侧腰线中取点的连线AB,由于视觉特征点一般会选取腰线棱边靠近两端处,而A、B点必能落在视觉特征点的连线内,图4所示A、B点将分别都在视觉特征点4与5的连线及视觉特征点2与3的连线上,由上文推导可知A点、B点、Oc的重复精度与单个的视觉特征点重复精度一致,由设备定位原理可知中心点的重复精度实际即为设备的视觉引导的重复精度,则可得下式(2)的结论。
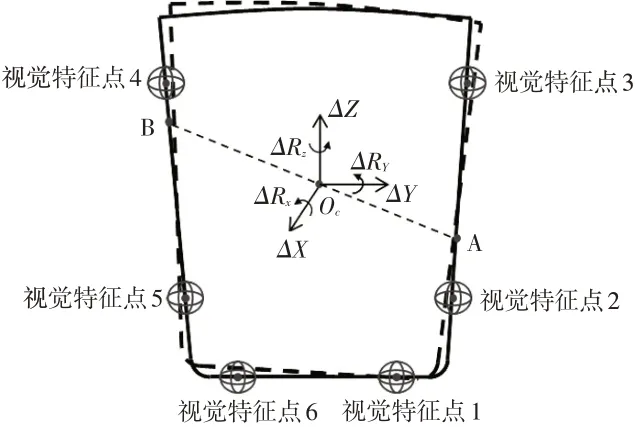
图4 顶盖钣金中心点拟合示意
即得视觉定位重复精度如下:
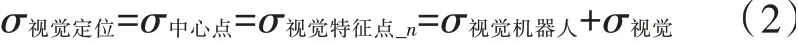
3.2.2 对中定位能力计算模型
对于对中定位精度,由于对中台的形式一般如图5所示,X向一侧为固定柱,X向另一侧为夹紧柱,而Y向通过对中气缸及齿形带传动进行居中夹紧对中。在不考虑X向固定柱磨损的情况下,从设备角度上来看,X向定位不会产生偏差,但Y向受气缸及传动影响,在对中台上的位置产生一定波动,偏差值如下:
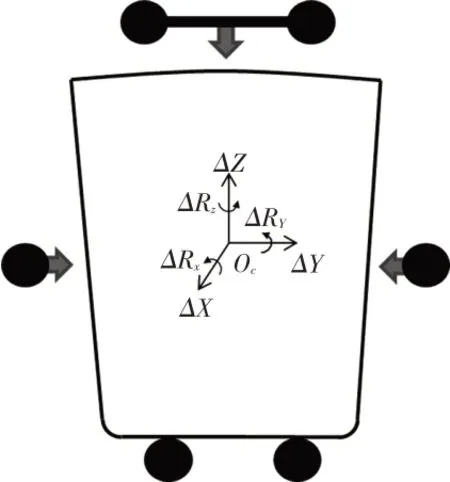
图5 对中台示意

同时,安装机器人抓取对中台中的零件时,受安装机器人精度影响,也会产生一定偏差,且安装机器人在Z向的偏差能被抓取夹具上的吸盘补偿,即此步骤精度为机器人在三维上的重复精度在XY平面上的投影,则抓取动作偏差值为:

3.2.3 安装定位能力计算模型
对于安装定位精度,受安装机器人精度影响,其到达指定位置的值会存在一定偏差,即为:σ安装机器人。
综合上述三个环节,将导致最后实际零件中心点与理想状态下存在偏差,且此三个环节的精度偏差在空间上能直接叠加,则有设备精度为:

对于绕X、Y、Z轴旋转量的姿态精度,由于零件安装面会有垫块限制绕X轴和Y轴的旋转,同时由于角度偏差较小,对于零件类零件尺寸不大,其偏差值远小于上述平移产生的偏差大小。例如,1.4 m的零件,距离中心点最远处约0.75 m,中心点旋转量的偏差约为±0.1°,则坐标变化值约为0.001 mm,此偏差值对最后装配影响可忽略,所以对姿态精度不做具体计算。
由于零件中心点在X、Y、Z三个方向的波动是相互独立的,其在X、Y、Z三个方向投影,可得设备在3个方向相应精度值为:

4 设备匹配质量能力测试
4.1 设备匹配质量测试流程
在对设备整个关键路径测试前,应首先保障单个关键组件自身运行的稳定性,以避免出现零位不稳定的现象。而整个过程流的关键组件是工业机器人与视觉系统,对于工业机器人,如图6所示,应在调试前对工业机器人各轴进行零点标定,使各轴的机械位置和电气位置保持一致,如若需要,可参照ISO 9283:1998[1]标准对其精度进行测试,验证其是否达到设计能力。同样,对于视觉系统应通过标定板对相机进行标定,如图7所示,保证视觉采集的一致性,如若需要,可通过静态测试对其重复精度进行测试,即相机重复对某一固定特征点进行拍照获取其坐标值,通过计算其坐标的变化量亦可验证其是否达到设计能力。由于自动涂胶安装类设备稳定性测试的难点在于对整个设备的测试,且行业内缺少相关的论述,本研究将重点围绕对整个设备的测试进行阐述。

图6 工业机器人零点标定示意

图7 视觉标定示意
由设备原理及设备能力模型可知,零件的安装精度实际是零件中心点相对于车身顶盖钣金的中心点位置的偏差量。但此偏差值无法直接测量,而需要通过其他参数进行测量量化。在实际生产中通过零件与车身钣金的间隙与平度来衡量匹配质量的优劣(图8)。本研究也将通过此参数量化匹配质量相关的间隙、平度范围。
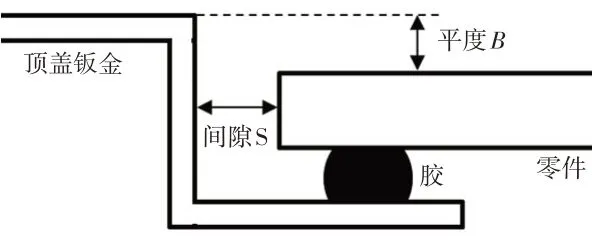
图8 匹配示意
刚体上任意不在一条直线上点能确定刚体的位置。则如果安装后的零件中选取的不在一条直线上的三点即可确定整个零件相对于顶盖钣金的位置。即测试设备安装的稳定性时,可测量监控零件上不在直线上的3点相对于顶盖钣金的位置值,由于只考虑零件整体平动的影响,若此3点的位置值是稳定的,则零件上任意一点相对顶盖钣金位置值也是稳定的,即可得到最终的匹配质量稳定的结论。
则测试流程可对图3关键路径进行还原模拟,步骤如下。
a.通过机械化将车身驶入安装工位,定位机构将滑翘抱死;
b.启动设备,设备按照程序设定,安装机器人从对中台中抓件,不带胶空走涂胶轨迹,同时视觉完成拍照及补偿值计算与发送,安装机器人将零件恰好放至安装位时,将安装机器人停止;
c.以图9为例,测量并记录P1、P2、P3间隙平度值,将零件、车身还原至测试前状态,继续后续轮次测试。
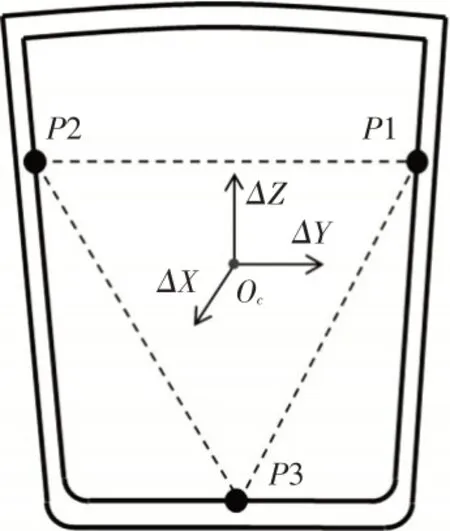
图9 测试过程测量点示意图
d.完成设定轮次的测试后,根据4.2内容计算匹配稳定性Cm,判断测试结果是否合格。
4.2 设备匹配能力计算模型
由以上分析可知,设备精度是在世界坐标下的X/Y/Z轴的波动量,而实际现场测试时无法获取此3点的坐标值,需要将其转换为测量点的平度与间隙值的波动量。
如下图所示,对于轮廓纵向类的测量点,如P1点,假设P1点在理想位置时,其间隙值大小为S,平度为B。当P1在精度范围内波动时,如图10所示,其在X/Y方向的波动将导致该点间隙值的变化,其中Y方向的变化量将直接转化间隙值的变化,X方向的变化导致顶盖钣金的基准点也平行移动,而将产生K×ΔX的间隙变化值,K为顶盖钣金在选定点处的斜率。同样的在Z轴方向的波动,如图11所示,将产生等量的平度值变化。
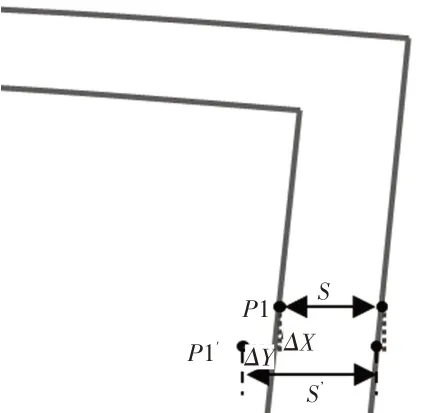
图10 纵向测量点间隙匹配波动示意
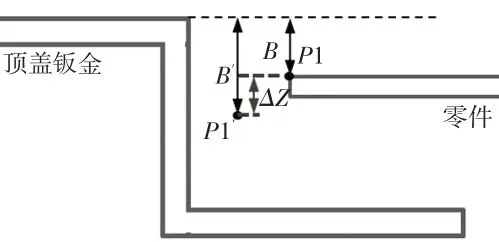
图11 纵向测量点平度匹配波动示意
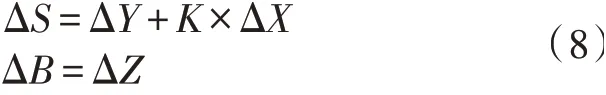
其中,K为顶盖钣金基准点在其轮廓线上的斜率。
根据上文可知设备在X、Y、Z轴上的精度范围,则对应的各测量点的间隙平度的波动范围应为:
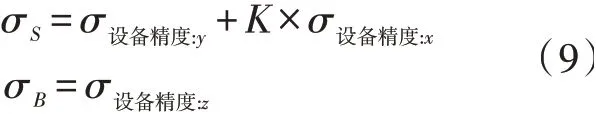
同样的,对于轮廓横向类的测量点,其波动状态如下图所示,由于该处测量基准点的变化不影响间隙值的测量大小,同样的Z轴方向的波动,如图12所示,将产生等量的平度值变化,则有其表达式为:
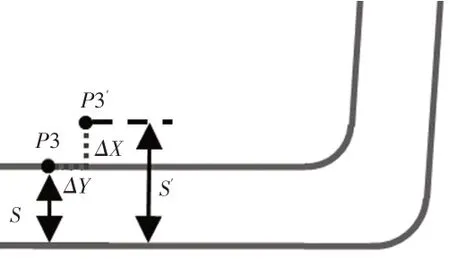
图12 横向测量点匹配波动示意

则对应的波动范围计算如下:

由于在稳定性测试中,实际设备不一定能将安装质量调至最佳位置,而可采用不考虑偏移的过程能力Cm来衡量设备的稳定性。
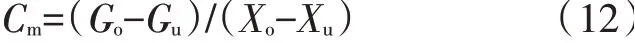
式中,Go,Gu分别为设备能力值的上公差和下公差Xo,Xu分别为设备能力测试中样本数据中的最大值和最小值。
根据各测量点的间隙、平度值,计算可得设备能力如下:
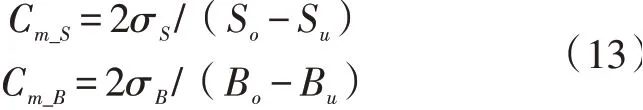
即若测量的3点都在稳定范围内,则设备的稳定性定能达到设计能力。则衡量设备稳定性是否满足达到指标公式为:
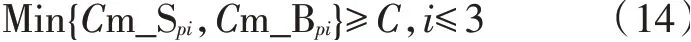
式中,C为稳定性合格值(表1)。
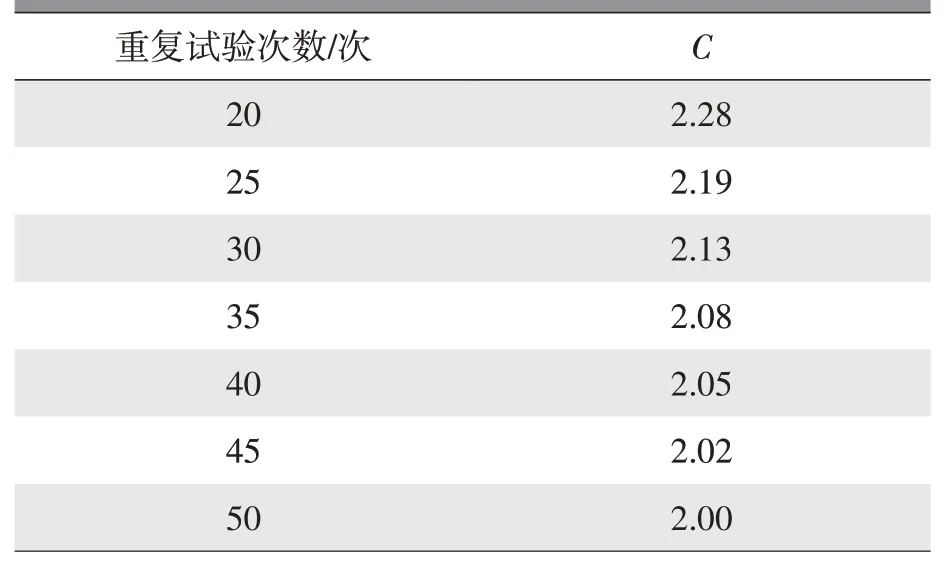
表1 试验次数稳定性合格值[3]
同时,在实际测试中,为提高测试效率及降低测试时间跨度对结果的扰动,应尽量将测试点范围控制在合理范围。若评估整体的匹配质量稳定性,最少只需选定3个点的间隙值测量,和其中一个点的平度值测量,3点所构成的区域应覆盖零件中心点,即i取3的情况。若只关心某些匹配点稳定性,则只需对这些匹配点进行测试即可,相应的i为相应的点个数。
5 实际案例
在实际测试中,应排除设备以外影响最后装配效果的因素,需注意如下事项。
a.应使用同一个车身,同一个测试件,测试件应尽量采用不易变形的材料对零件进行仿形,以减少测试造成的零件形变对匹配结果的影响;
b.采用不带涂胶的形式进行,同时为保证测量的一致性,应在对测量点进行标记,保证每一次测量都是在标记测量点进行测量,同时测量时不得晃动车身;
c.应根据实际需求,确定测试范围以提升测试的效率和准确性。若进行整体测试,则对选定的三个点进行间隙的测量和三点中任意一点的平度值测量即可,并计算出此四个测量值Cm值判定即可。若局部测试,则只需测量和计算局部值即可;
d.应在选定测试轮数上增加2次,以去掉1个最大值和1个最小值后为数据样本。若采用原玻璃零件,建议进行22次,而采用C_20=2.28作为稳定性判定值。
本案例为局部测试,项目阶段P1、P2处间隙值出现了异常匹配波动,而针对此两点进行了测试。本案例测试数据如表2所示。
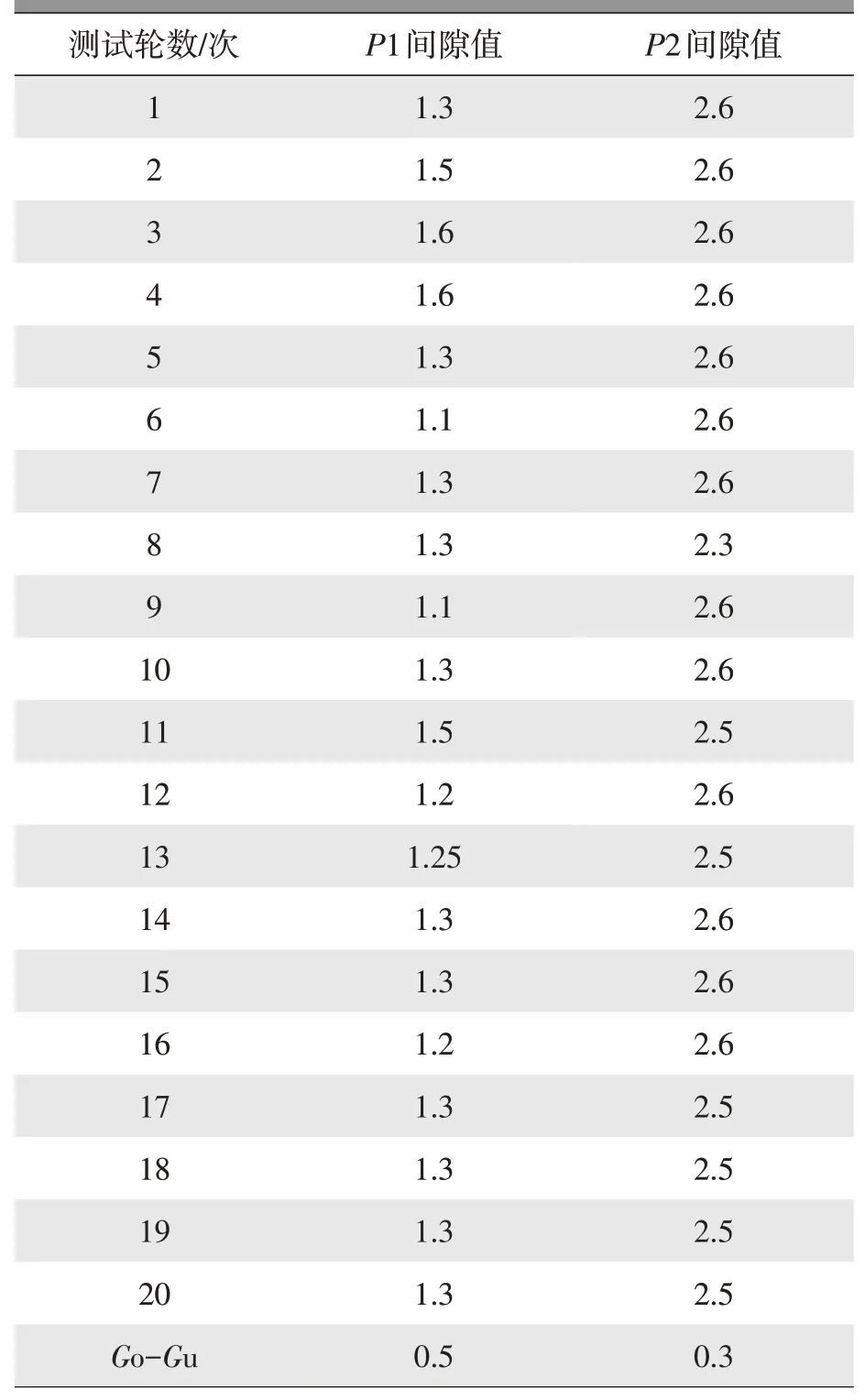
表2 测试过程数据 mm
而根据设备的技术选型,σ安装机器人及σ视觉机器人为±0.1 mm(含机器人抓手吸盘、连接件轻微震动等相关因素),σ视觉为±0.2 mm,σ对中:y为0.05 mm(含气缸及齿形带等),则根据式(7)得出σ设备精度:x为±0.5 mm,σ设备精度:y为±0.55 mm,同时,P1及P2点在车身上对称,斜率正切值K为0.04,即而可得σS_P1及σS_P2为±0.57mm,据式(13)可得到能力值Cm_P1=2.28,Cm_P2=3.8。Cm_P1及Cm_P2都大于C_20,可得出P1及P2两点在间隙值是稳定的。
同时从数据可以看到P1点的间隙波动量较P2点明显更大。进行复盘时,初步判断原因为P1点所在一侧,设备围栏与车身距离较近,给测量预留空间较小,测量难度较大,测量时测量人员易倚靠车身,造成该侧测量值出现扰动因素。
综上所述,对风挡、全景天窗全自动化涂胶安装设备的能力分析及验证工作中,通过文中设备能力计算模型,可得出设备稳定性能力值,而由于该值较难进行实际测量,通过匹配能力计算模型,将该设备能力值转化为实际安装的间隙匹配的波动范围,最后通过匹配质量的稳定性测试方法,实现对设备能力的验证。
