基于MapReduce和改进人工蜂群算法的并行划分聚类算法
2021-08-20毛伊敏
陶 涛,毛伊敏
(江西理工大学信息工程学院,赣州 341000)
聚类分析作为数据挖掘中一种无监督学习过程,可以通过数据对象的相关特征,把类似的数据对象划为一类,而具有较大差异性的数据对象则划到不同类,因此聚类分析可以从样本数据中发现隐藏的分布模式,在图像分割、信息检索系统、异常检测、计算机视觉和施工管理等领域广泛应用[1]。在聚类算法中,基于划分的聚类算法,如K-means[2-3]和K-medoids[4]算法,具有简单易理解、算法收敛速度快等特点,受到人们的广泛关注。
随着互联网技术的快速发展以及大数据时代的到来,使得大数据相较于传统数据,具有了体积大(volume)、种类多(variety)、速度快(velocity)、价值高(value)的“4V”特性[5]。但由于传统的划分聚类算法在处理大数据集时,时间复杂度较高,只适用于小规模的数据集。所以,如何降低划分聚类算法的计算复杂度,使其能处理大数据,是个关键性的难题。
近年来,随着Google公司成功研发了MapReduce框架,以Hadoop、Spark为代表的分布式计算架构受到了越来越多的青睐[6-7]。为进一步降低划分聚类算法的计算复杂度,将传统的划分聚类算法进行改进,同时结合分布式计算架构,成为当前划分聚类算法的研究热点。Cui等[8]最早提出了大数据下基于MapReduce的K-means优化聚类算法,为解决K-means聚类算法处理大规模数据时,迭代次数多和性能较低的问题,该算法利用MapReduce框架实现定义了映射(Map)函数和规约(Reduce)函数,消除了迭代依赖,但是聚类算法中未进行参数寻优,从而会影响聚类稳定性。为了进一步提高聚类稳定性,唐新宇等[9]提出了一种基于群体智能的大数据聚类算法,通过采用混合蛙跳算法来优化C-means 算法,以便调整参数,从而提高全局搜索能力。Qian等[10]使用群智能优化算法,进行全局搜索,在利用Spark进行并行化。虽然这些算法进行了一定程度的参数寻优,但参数寻优能力依然不佳,此外,这些算法的并行化都未考虑到随机选取初始聚类中心,引起的初始中心敏感的问题。
如何解决随机选取初始聚类中心,引起的初始中心敏感的问题,一直是基于划分的并行化聚类算法的重要研究内容。为了处理这个问题,阴爱英等[11]提出一种基于MapReduce框架下K-means的改进算法,该算法通过凝聚层次聚类法对大数据集进行聚类,从而获取初始聚类中心,降低了最终聚类结果对参数的敏感程度。李媛媛等[12]提出云环境下并行的K-medoids算法,算法利用最大最小原则和密度法获取优化的初始聚类中心,然后在Canopy区域里进行中心点替换。虽然这些算法都对传统的随机选取中心点进行了改进,但是没有完全解决初始中心敏感的问题。袁逸铭等[13]使用基于密度峰值的快速搜索算法获取初始中心点,然后通过MapReduce框架进行并行化。除此之外,这些算法都未考虑并行时数据倾斜的问题,导致集群效率低下,极大降低了整体并行化的运行效率。针对这个问题,周华平等[14]提出了基于索引偏移的MapReduce聚类负载均衡策略,通过将更改剩余分区索引的策略应用于解决数据的不均匀划分。虽然目前基于划分的并行化聚类算法的研究已经取得了一些成果,但如何进一步处理划分聚类算法中参数寻优能力不佳,如何进一步降低随机选取初始聚类中心引起的初始中心敏感的影响,如何解决数据倾斜的问题,从而提高并行化聚类算法的整体性能,仍是目前亟须解决的问题。
针对以上问题,现提出基于IABC的并行划分聚类(the partitioning-based clustering algorithm using improve artificial bee colony based on MapReduce,MR-PBIABC)算法,主要工作为:提出基于反向学习和聚类准则函数的初始化策略(backward learning and the clustering criterion function,BLCCF),提升人工蜂群算法搜索的解质量,并将人工蜂群(artificial bee colony,ABC)算法和人工鱼群(artificial fish colony,AFS)算法结合,提出改进的人工蜂群算法(improve artificial bee colony,IABC),通过利用AFS算法最优解能力较强的特性,提高ABC算法的寻优能力;根据改进的人工蜂群算法IABC获取初始聚类中心,并提出相对熵策略(relative entropy strategy,RES)衡量人工鱼间的距离,保证获得的初始聚类中心是最优人工鱼状态;设计数据均衡策略(data balancing strategy,DBS),通过动态收集节点负载并分配节点间的负载,解决节点上数据倾斜的问题;在MapReduce计算模型下,并行挖掘簇中心,生成最终聚类结果。
1 相关技术概念
1.1 MapReduce计算模型
MapReduce是一种简化的分布式编程模型和高效的任务调度模型[15],用于大规模数据集的并行运算。MapReduce编程模型的核心在于Map(映射)阶段和Reduce(化简)阶段的实现,Map阶段是将输入的
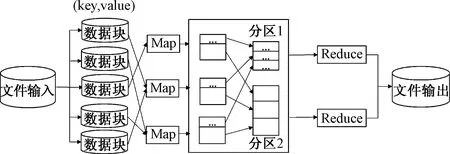
图1 MapReduce模型
1.2 反向学习
反向学习[16]是为了生成反向解,其定义是在d维空间的一个候选集p=(x1,x2,…,xd),其中xi∈[ai,bi],i=1,2,…,d,则其对应的反向解为p=(x′1,x′2,…,x′d),其中x′i=ai+bi-xi。
1.3 人工蜂群算法
人工蜂群算法[17]是模仿蜜蜂行为的一种基于集群智能思想的方法,主要由雇佣蜂阶段、跟随蜂阶段、侦查蜂阶段组成。
(1)雇佣蜂阶段。产生随机候选解为
vij=xij+φij(xij-xkj)
(1)
式(1)中:xij为第i个蜜源的第j维分量;xkj为随机选取的异于xij的蜜源;k∈{1,2,…,NS};φij∈(-1,1)。
(2)跟随蜂阶段。返回雇佣蜂的蜜源信息,根据蜜源的适应度yi按式(2)计算食物源被选中的概率Pi,当yi越大,则Pi越大。
(2)
式(2)中:yi为蜜源的适应度,与蜜源i的目标函数值有关;NS为蜜源的个数。
(3)侦查蜂阶段。达到开采上限时,如果适应度仍未更新则被淘汰。
1.4 人工鱼群优化算法
人工鱼群算法[18]是根据鱼类的活动特点提出的一种基于动物行为的自治体寻优模式,主要由觅食、聚群、追尾行为组成。
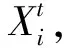
(3)
式(3)中:Visual为人工鱼的视野;Rand()为随机函数。
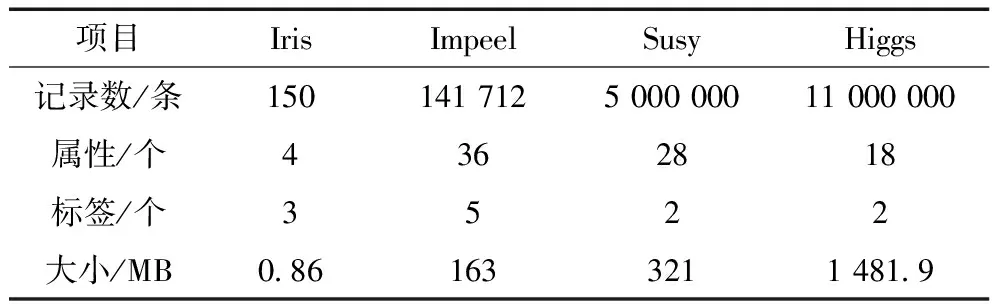
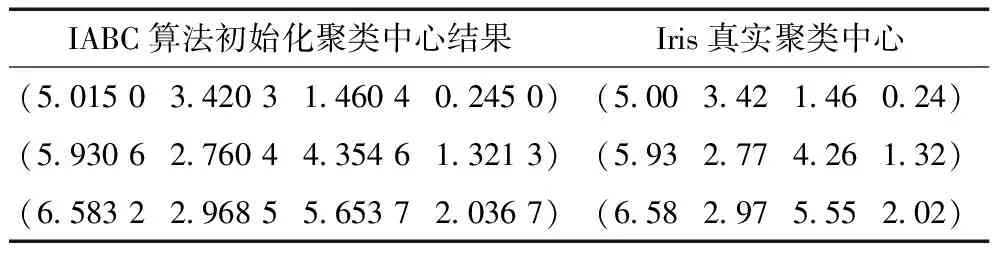
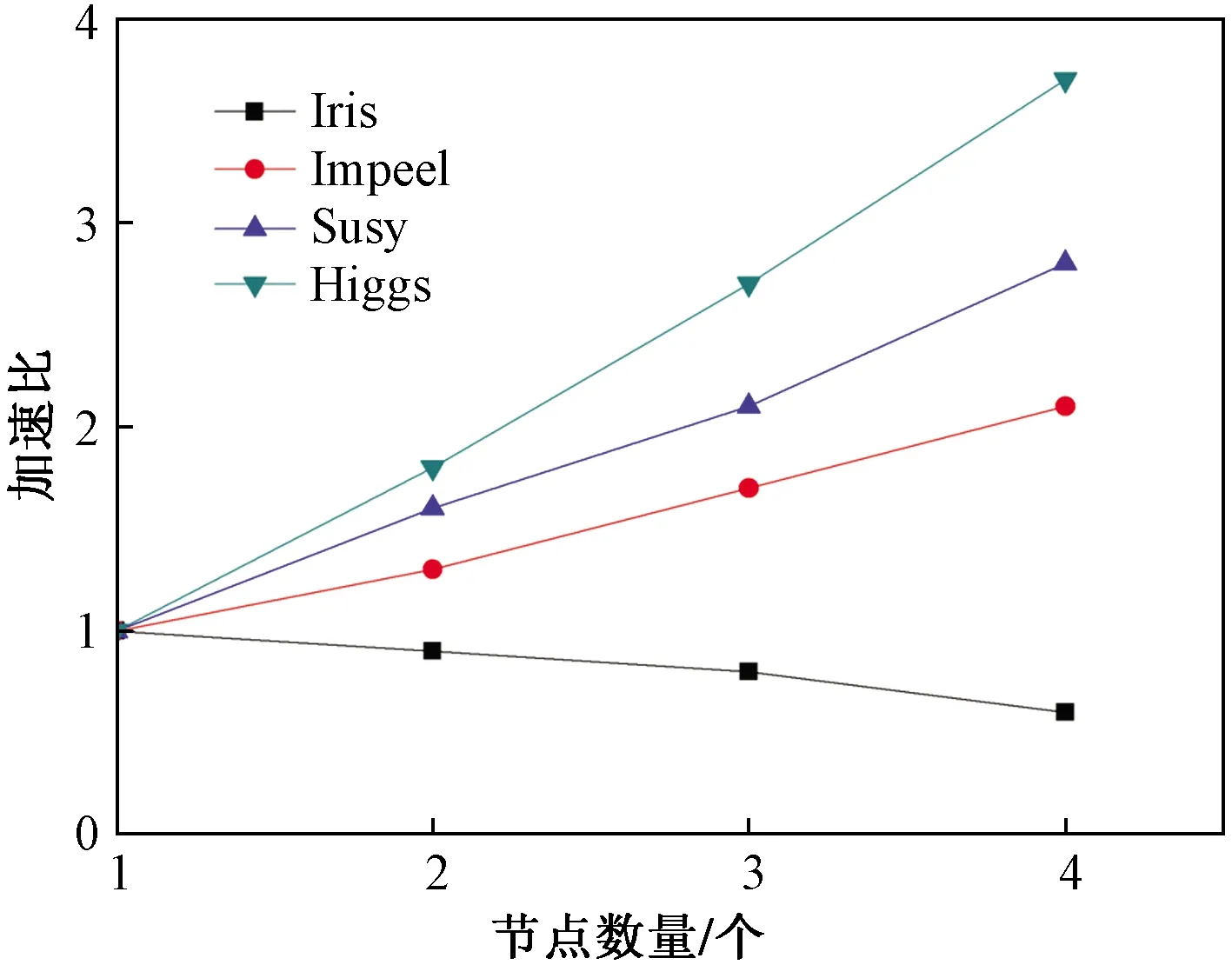
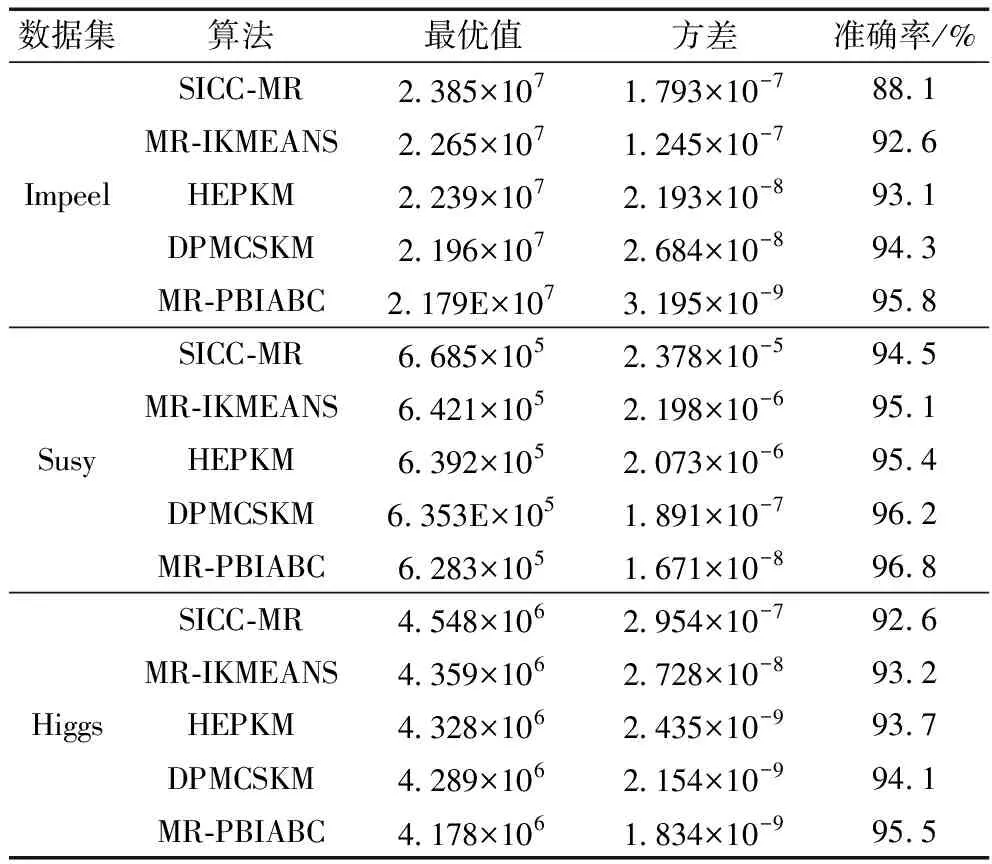
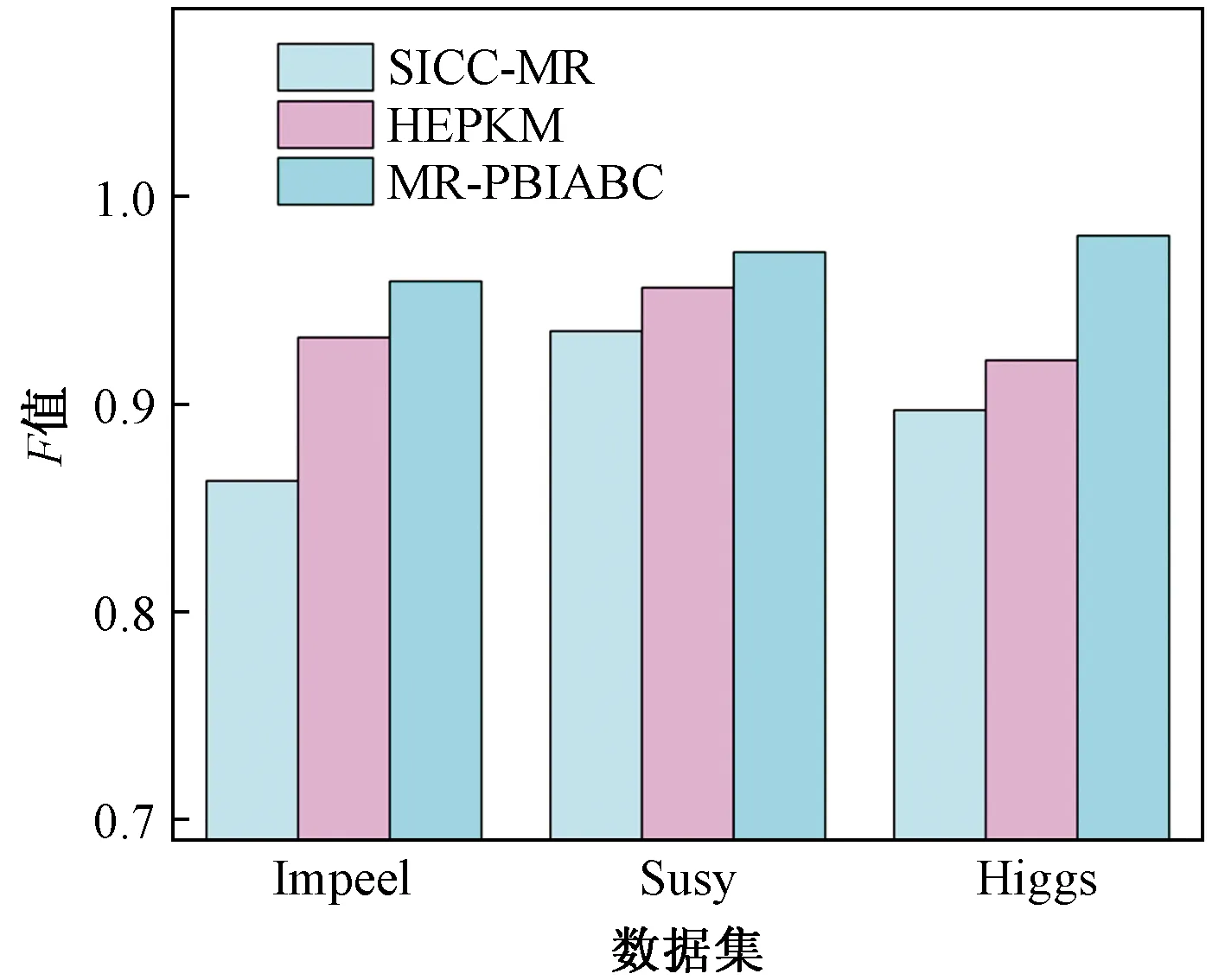
若Yi (4) 反之,再重新随机选取状态Xtry,如果Yi>Ytry,则重复NTry次后,当依然Yi>Ytry,则任意前进一步,即 (5) (6) 否则,执行觅食行为。 (7) 否则,执行觅食行为。 MR-PBIABC算法主要包括3个阶段:数据预处理、数据均衡和并行划分聚类。 (1)在数据预处理阶段。首先提出基于反向学习和聚类准则函数的初始化策略BLCCF,来提升人工蜂群算法搜索的解质量,并将人工蜂群算法(ABC)和人工鱼群优化算法(AFS)结合,提出改进的人工蜂群算法IABC,通过利用AFS算法最优解能力较强的特性,来提高ABC算法的寻优能力;然后根据改进的人工蜂群算法IABC获取初始聚类中心,并提出相对熵策略RES衡量人工鱼间的距离,保证获得的初始聚类中心是最优人工鱼状态,从而有效避免了随机选取初始聚类中心,引起的初始中心敏感的问题。 (2)在数据均衡阶段。设计数据均衡策略 DBS,通过动态收集节点负载并分配节点间的负载,解决了节点上数据倾斜的问题。 (3)并行划分聚类阶段。在MapReduce计算模型下,并行挖掘簇中心,生成最终聚类结果。 目前大数据环境下的并行划分聚类算法中,通常采用群智能优化等策略有效改进参数敏感问题,但也仍然存在参数寻优能力不佳,并对初始数据集,通常采用随机选取初始聚类中心,这种选取方式会对聚类结果有较大影响,从而产生初始中心敏感的问题。针对这些问题,提出基于反向学习和聚类准则函数的初始化策略BLCCF,来提升人工蜂群算法搜索的解质量,并将ABC算法和AFS算法结合,通过利用AFS算法最优解能力较强的特性,来提升ABC算法的寻优能力;然后根据改进的人工蜂群算法IABC获取初始聚类中心,并提出相对熵策略RES衡量人工鱼间的距离,保证获得的初始聚类中心是最优人工鱼状态,有效避免随机选取初始聚类中心引起的初始中心敏感的问题。 2.2.1 IABC算法 为了进一步提高算法对聚类参数的寻优能力,提出基于反向学习和聚类准则函数的初始化策略BLCCF,来提升ABC算法搜索的解质量,并将ABC算法和AFS算法结合,提升ABC算法的寻优能力。 首先,在种群初始化阶段,提出基于反向学习和聚类准则函数的初始化策略BLCCF,以提升ABC算法搜索的解质量,初始化策略BLCCF步骤如下。 步骤一在d维数据空间中,随机获取K个蜜源位置,根据蜜源选择式(2)生成种群规模|K|,其集合为Xi=(x1,x2,…,xk);然后根据反向学习算法,得到反向种群Xi*=(x1*,x2*,…,xk*),合并两组解得X=(Xi∪Xi*),计算适应度δ(X)=(δ(Xi)∪δ(Xi*),按照适应度从小到大排序,选取前K个作为top-K解,从而使种群个体尽可能均匀分布在数据空间。 步骤二根据聚类特性,即簇内项相似性最大、簇间项相似性最小的原理,提出聚类准则函数CCF,使生成的top-K更符合聚类特性,进而提高聚类效果。 定义1(聚类准则函数CCF):若种群的个数为K,种群i中个体的数量为Ki,则其聚类准则函数CCF定义为 (8) 聚类准则函数的前半部分是评价簇内的稳定性,若值越大,说明簇内部越稳定,聚类效果越好;后半部分是评价簇间的稳定性,若值越小,说明簇与簇之间的关联性较小,聚类效果更好。 然后,在生成初始化种群后,ABC算法虽然具有较强的全局搜索能力,但未利用最优解进行搜索,会导致算法寻优能力较差,因此提出改进的人工蜂群算法IABC,利用AFS算法寻求最优解较强的特性,使用式(3)~式(7)更新参数,从而提升ABC算法的寻优能力。 2.2.2 初始簇中心获取 在提出IABC算法之后,对初始数据集,采用IABC算法获取初始聚类中心,其具体步骤如下。 步骤一进行种群初始化,得到种群规模top-K,并采用聚类准则函数CCF评价种群top-K。 步骤二根据AFS算法利用最优解较强的特性,将top-K作为初始人工鱼,根据式(3)~式(7)执行人工鱼的觅食、聚群、追尾行为。 步骤三提出相对熵策略RES衡量人工鱼间的距离,通过增大人工鱼群内相似性,群间差异性,从而能获得最优人工鱼群状态,通过迭代执行上述步骤,得到更新后的k个人工鱼群。 定义2(相对熵策略 RES):假设a,b表示不同的人工鱼,人工鱼的k分类模型为Xk×d,其中k为分类数,d为数据维度,则人工鱼间的相对熵定义为 (Xmd)a=(xm1a,xm2a,…,xmda) (9) (Xmd)b=(xm1b,xm2b,…,xmdb) (10) (11) (12) (13) 式中:(Xmd)a为Xk×n中第m(1≤m≤k)分量结构;X′md(x)a、X′md(x)b分别为人工鱼a、b的概率分布。 证明:当相对熵D(Xa‖Xb)越大,则人工鱼a与b的差异越大;反之,差异越小。通过迭代执行上述步骤,并使用相对熵可以将人工鱼群进行分类,进而增大鱼群间的差异性和鱼群内的相似性,可以产生最优人工鱼{F1,F2,F3…,Fk},从而能生成初始聚类中心。证毕。 最后,记录最优人工鱼群状态,即作为初始中心点。过程伪代码如下。 算法1初始簇中心获取 输入:数据集D(n个数据对象,m个维度),聚类数k 输出:k个初始聚类中心 (1)According to BLCCF strategy; (2)Get top-K;//种群初始化 (3)Then use CCF to estimate top-K; (4)top-Kas initial artificial fish;//top-K作为初始人工鱼 (5)Carry out the formula(3)~formula(7); (6)Then useD(Xa‖Xb)to measure the distance between artificial fish; (7)IfD(Xa‖Xb)smallest (8) Explain little difference betweenaandb; (9) Update artificial fish swarm; (10) Then record optimal artificial fish;//记录最优人工鱼状态 (11) Get{F1,F2,…,Fk}; (12)Then set asO;//设置最优人工鱼为初始簇中心 (13)O={F1,F2,…,Fk}; (14)ReturnO 在用IABC算法获取初始簇中心后,为了进一步提高并行效率,避免节点间数据倾斜,设计数据均衡策略 DBS,通过动态收集节点负载并分配节点间的负载,解决了节点上数据倾斜的问题。DBS策略为:当把过载的Reducer节点上的数据量进行任务调度时,会产生一定的系统开销,如果大于继续保留在原节点的开销,反而会降低集群的效率。因此设计了数据均衡策略DBS,处理节点上的数据倾斜。 定义3(数据均衡策略DBS):若节点i过载时未处理的数据量为L(i)m,Reducer上系统悬挂和恢复的时间开销为Ts和Tr,任务调度时的通信开销为Tc,则其数据均衡策略如下: (14) T(i)m>2Ci (15) Ci=Ts+Tc+Tr (16) 式中:T(i)m为节点i过载时的时间开销;Ci为过载节点进行数据调度的总时间开销。 证明:因为T(i)m和L(i)m为节点上动态获取的时间开销和过载数据量,通过T(i)m>2Ci表明进行调度时产生的时间开销小于在过载节点的时间开销,从而满足调度条件,所以能达到调度后,时间开销减小,解决了节点上的数据倾斜,提高了并行效率。证毕。 “DBS”策略伪代码如下。 算法2“DBS”策略 输入:数据集D,Reducer节点数r 输出:数据均衡结果 (1)While reducerpbecome idle;//DBS策略触发条件 (2)T(i)m=maxTi(1≤i≤r); (3)L=L-L(p);//去除完成节点的负载 (4)IfL≠0 do (5)If Schedule-Lock==false do (6) Wait for the Schedule-Lock; (7)Schedule-Lock==true;//获得调度锁 (8) Else ifT(i)m>2Cido (9)q=get Reducer ID(Lmax);//获得负载最重的节点 (10)Stopqand getLm;//记录划分结果 (11) DivideLmequally and transmit top,q; (12) Restartp,q; (13) Schedule-Lock==false;//释放调度锁 (14) End if (15)End if (16)Return data balancing results; 在数据均衡后,为了并行挖掘簇中心,获取最终聚类结果,要调用Map和Reduce任务。在Map阶段,它的主要任务是读取初始聚类中心和数据均衡结果,随后根据欧式距离公式获得数据对象到初始簇中心的距离,将数据对象分配给各个簇,得到局部聚类结果并将结果暂时存入Combine。在Reduce阶段,其主要任务是接受Combine内的局部聚类结果,合并局部簇,随后根据代价函数E[19]判断是否得到全局最优解,当Emin不成立时,启用新的MapReduce任务进行迭代,直到Emin时,得到全局最优解,从而取得最终聚类结果,且聚类过程结束。执行过程伪代码如下。 算法3并行划分聚类 输入:初始簇中心,数据均衡结果 输出:最终聚类结果 (1)Enable MapReduce (2)Map(key,value) (3)InputOand Data balancing results; (4) Get the local clustering results;/*根据欧式距离得到局部聚类结果*/ (5) Deposit in Combine;//结果暂存入Combine (6)End (7)Reduce(key,value) (8) Read Combine; (9) IfEmin= false do (10) Enable a new MapReduce task;/*启用新的MapReduce任务 (11) Else do (12) Get the final clustering results;//得到最终聚类结果 (13) End (14)End (15)Returnthe final clustering results; 步骤1通过基于反向学习和聚类准则函数的初始化策略,初始化种群,得到种群规模top-K。 步骤2将ABC算法和AFS算法结合,提升ABC算法的寻优能力,提出改进的人工蜂群算法。 步骤3通过改进的人工蜂群算法获取初始聚类中心。 步骤4并根据相对熵策略RES衡量人工鱼间的距离,保证获得的初始聚类中心是最优人工鱼状态。 步骤5在数据均衡阶段,调用算法2的DBS策略,通过动态收集节点负载并分配节点间的负载,进行数据的合理划分,解决节点上数据倾斜的问题,得到数据均衡结果。 步骤6读取初始聚类中心和数据均衡结果,启用MapReduce任务,调用算法3完成并行划分聚类,从而获取最终聚类结果。 2.6.1 时间复杂度 MR-PBIABC算法的时间复杂度主要由数据预处理,数据均衡,并行划分聚类这几个步骤构成,分别记作T1、T2、T3。 首先在BLCCF策略进行种群初始化阶段,假设空间中数据点的数量为n,初始种群数为K,则种群初始化的时间复杂度为 Tc=O(Kn2) (17) 在IABC算法获取初始聚类中心阶段,其时间复杂度主要取决于迭代更新最优人工鱼状态的运算,则其时间复杂度为 (18) 因此数据预处理的时间复杂度为 (19) 在数据均衡阶段。假设Reducer节点的数量为r,通过采用DBS策略均衡节点间的数据量,完成合理的数据划分,其时间复杂度为 T2=O(n/r) (20) 并行划分聚类阶段。需要进行多个MapReduce任务,并行的更新每个簇,其时间复杂度为 T3=O(rlog2n) (21) 因此MR-PBIABC算法的时间复杂度为 (22) 而DPMCSKM[12]算法中,算法的参数寻优能力不佳,初始簇中心选取未解决且未考虑节点间的数据倾斜,故其时间复杂度为 (23) 在大数据环境下,T1>>T2,T3,而且通过初始簇中心获取后,极大减少了迭代次数,即T1-MR-PBIABC≫T1-DPMCSKM,因此MR-PBIABC算法时间复杂度远低于DPMCSKM算法。 2.6.2 空间复杂度 MR-PBIABC算法的空间复杂度是更新簇中心所占内存和负载均衡节点队列占用的内存之和,假设数据量为n,簇的个数为k,Reducer节点数为r,算法的迭代次数为e,则MR-PBIABC算法的空间复杂度为 (24) DPMCSKM[12]算法的空间复杂度主要是更新簇中心所占内存,但该算法未进行初始簇中心获取,因此其空间复杂度为 MDPMCSKM=O(klog2n+n2) (25) 由于大数据环境下,负载均衡节点队列所占内存远小于参数存储内存,因此内存主要是更新簇中心,而MR-PBIABC算法通过初始簇中心获取后,参数数量远小于DPMCSKM算法,故MR-PBIABC算法空间复杂度远小于DPMCSKM算法。 为验证MR-PBIABC算法的聚类效果和并行效率,设计了相关实验。实验环境包含由1个Master节点和3个Slaver节点构成的Hadoop集群,节点间通过300 Mb/s网络相连,且4个节点的配置相同:硬盘1 TB,内存16 GB,CPU为Inter core i7-9750H,操作系统为Ubuntu 16.04, 安装Hadoop版本2.7.4,采用Java JDK1.8.0编译。 MR-PBIABC算法采用的实验数据为4个来自UCI公共数据库的真实数据集,分别是Iris、Impeel、Susy和Higgs。Iris是模式识别文献中最著名的数据集,包含150条数据,具有数据量小等特点;Impeel是从IT公司使用的ServiceNowTM平台实例的审计系统收集的数据,该数据集有141 712条实例,具有多元、记录长度长等特点;Susy是一组有关粒子加速器探测粒子的数据,该数据集有5 000 000条记录,具有数据量大,数据均匀等特点;Higgs包含11 000 000条数据,具有数据量大、数据离散等特点。数据集的详细信息如表1所示。 表1 实验数据集 3.3.1 加速比 为验证MR-PBIABC算法在大数据集下并行处理的能力,采用加速比来衡量并行计算的性能。加速比是指在并行计算下,降低运行时间从而获得的性能提升,其定义为 Sp=T1/Tp (26) 式(26)中:T1为算法在单节点上的运行时间;Tp为并行计算的运行时间。Sp越大,则表示并行计算所耗费的相对时间较少,集群的效率得到提升。 3.3.2F值 为验证MR-PBIABC算法对数据集的聚类效果,使用F值对聚类结果进行评价,F值是正确率(precision,P)和召回率(recall,R)的加权平均值,其定义为 (27) 式(27)中:P为正确率;R为召回率。通常情况下,参数λ=1,F值综合考虑了聚类结果的正确率和召回率的情况,能够较为准确地评价聚类算法的结果,当F值较高时,说明聚类效果较好。 为验证IABC算法的有效性,运用IABC算法对Iris数据集进行初始聚类中心的选取,并与Iris数据集的真实中心进行比较,如表2所示。 表2 初始聚类中心对比 从表2可以看出,在Iris数据集上,IABC算法得到的初始聚类中心和真实聚类中心非常相似,误差在百分数级别,这说明了IABC算法能够优化初始聚类中心的求取结果,为后续获得最终聚类结果打下了较好的基础,验证了IABC算法的有效性。 为验证MR-PBIABC算法在大数据集下并行处理的能力,加速比通常被作为检验并行化算法性能的重要指标,可以使用加速比来衡量并行计算的性能。通过在Iris、Impeel、Susy、Higgs 4个数据集的基础下,进行了多次实验,从而实现对MR-PBIABC算法性能的综合评估,算法的平均加速比曲线如图2所示。 图2 MR-PBIABC算法的加速比曲线 从图2可以看出,MR-PBIABC算法在Impeel、Susy和Higgs 3个大数据集下表现出很好的加速比性能。在处理Iris这样的小数据集时,随着节点数量的增加,加速比呈下降趋势且小于1,这是由于处理小数据集时,将数据分散到各个节点反而增加了各节点间的时间开销,加速比容易陷入瓶颈,因此并行算法不适应于小数据集。而在处理数据量较大的Higgs时,算法在4个节点下的加速比为3.7,比单节点提升2.7,原因是随着数据规模的增大,MR-PBIABC算法可以降低节点间通信开销和并行的进行簇的生成的优点被逐渐放大,在节点数量增加的同时,加速比曲线接近于线性增长,算法的并行性能表现出极大的提高。这也表明MR-PBIABC算法适用于处理大数据集,且随着节点数量的增加,并行化的效果更好。 为验证MR-PBIABC算法的综合性能,在Impeel、Susy和Higgs数据集下进行对比实验,根据聚类结果的最优值、方差、准确率、F值和运行时间,分别与SICC-MR算法[8]、MR-IKMEANS算法[10]、HEPKM算法[11]和DPMCSKM算法[12]进行性能比较。通过运行10次算法,得到的平均值作为实验的最终结果,从而实现对MR-PBIABC算法性能的综合比较。 3.6.1 聚类稳定性比较 为了验证MR-PBIABC算法的聚类稳定性,在上述3个数据集下进行对照实验,根据聚类结果的最优值、方差进行性能比较。其中最优值可以反映寻找最优解的能力,值越小表示寻找最优解的能力越强;方差体现算法的聚类稳定性;算法的聚类稳定性对比分析如表3所示。 表3 算法的聚类稳定性对比分析 从表3可以看出,SICC-MR算法相较于其他算法,聚类稳定性较差,这是由于SICC-MR算法只是对K-means进行了并行化,采用随机获取初始中心点的方式进行聚类,极大降低了算法的稳定性。而DPMCSKM算法利用最大最小原则和密度法获取优化的初始中心点,减小了随机选取初始中心的影响,一定程度上提高了算法的聚类稳定性。但由于密度法对异常值较为敏感,算法的稳定性受限。而MR-PBIABC算法通过基于反向学习和聚类准则函数的初始化策略BLCCF,提升人工蜂群算法搜索的解质量,并结合AFS算法,提高了ABC算法的寻优能力,根据改进的人工蜂群算法IABC获取初始聚类中心,同时提出相对熵策略RES,保证获得的初始聚类中心是最优人工鱼状态,从而有效避免了随机选取初始聚类中心,引起的初始中心敏感的问题,特别是在Susy数据集上,MR-PBIABC算法的方差值远小于其他算法,且在其他数据集下,最优值也最小,表现出良好的寻求最优解的能力,极大地提高了聚类稳定性。 3.6.2F值对比分析 为了分析算法的聚类效果,根据F值进行性能比较,F值可以明确地表现出算法聚类效果的好坏程度,在上述3个数据集下,分别与SICC-MR算法,HEPKM算法进行性能比较,得到的F值结果如图3所示。 图3 F值对比分析 从图3可以得出,HEPKM算法在几个数据集下的F值优于SICC-MR算法,尤其是在Impeel数据集上F值提高了5.1%。因为其采用凝聚层次聚类法获取初始聚类中心,在一定程度上缓解了SICC-MR算法没有考虑随机选取初始聚类中心导致的聚类结果不稳定的缺陷。而MR-PBIABC算法在F值上比HEPKM算法进一步提高了2.9%,这是由于MR-PBIABC算法采用改进的人工蜂群算法IABC获取初始聚类中心,提高了算法的寻优能力,且使初始簇中心相互之间的距离增大,提高聚类间的差异性,从而提升了算法的聚类效果。 3.6.3 运行时间比较 运行时间则表现算法的时间复杂度,通过在3种数据集下对5种算法的对比实验,可以进一步验证MR-PBIABC算法的性能,运行时间的对比分析如图4所示。 图4 3种数据集下各算法运行时间 从图4可以看出,相较于SICC-MR、MR-IKMEANS、HEPKM和DPMCSKM算法,MR-PBIABC算法在3个数据集上的运行时间均有所降低,其中在数据集Higgs降低最多,MR-PBIABC算法比SICC-MR、MR-IKMEANS、HEPKM和DPMCSKM算法的运行时间分别减少了61.1%、50.3%、42.5%和34.5%;在数据集Impeel上降低最少,但也分别减少了47.7%和39.3%,28.4%和16.5%。这是在Reducer节点间数据调度时,通过提出的数据均衡策略DBS,处理节点间数据倾斜的问题,提高了节点的利用率,进一步降低了MR-PBIABC算法的运行时间。 为解决基于划分的聚类算法在大数据背景下的不足,提出了基于IABC的并行划分聚类算法MR-PBIABC。首先,提出基于反向学习和聚类准则函数的初始化策略BLCCF,来提升人工蜂群算法搜索的解质量,并将人工蜂群算法(ABC)和人工鱼群优化算法(AFS)结合,提出改进的人工蜂群算法IABC,通过利用AFS算法最优解能力较强的特性,来提高ABC算法的寻优能力;接着根据改进的人工蜂群算法IABC获取初始聚类中心,并提出相对熵策略RES衡量人工鱼间的距离,保证获得的初始聚类中心是最优人工鱼状态,从而有效避免了随机选取初始聚类中心,引起的初始中心敏感的问题;其次,设计数据均衡策略 DBS,通过动态收集节点负载并分配节点间的负载,解决了节点上数据倾斜的问题,进而有效地提高了集群效率;最后,结合MapReduce计算模型,并行挖掘簇中心,生成最终聚类结果。为了验证MR-PBIABC算法的性能,在Iris、Impeel、Susy和Higgs 4个数据集下对MR-PBIABC、SICC-MR、MR-IKMEANS、HEPKM和DPMCSKM 5种算法进行性能对比分析,实验结果表明MR-PBIABC算法在处理数据量大且数据离散的球状簇时,具有更佳的聚类效果和寻优能力,且并行的效率也得到了很大提升。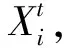
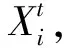
2 MR-PBIABC算法
2.1 算法思想
2.2 数据预处理
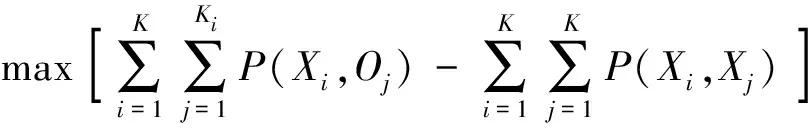
2.3 数据均衡
2.4 并行划分聚类
2.5 MR-PBIABC算法步骤
2.6 算法的复杂度分析
3 实验结果及比较
3.1 实验环境
3.2 实验数据
3.3 评价指标
3.4 IABC算法有效性分析
3.5 MR-PBIABC算法性能分析
3.6 MR-PBIABC算法性能比较

4 结论
