基于粒子群优化算法-支持向量回归算法的氨氮传感器温度补偿

姜吉光，盛宇博，常 川，石 磊，苏成志,2*，李 鑫

(1.长春理工大学机电工程学院，长春 130022；2.长春理工大学人工智能研究院，长春 130022)

水体中氨氮浓度是考核水质优劣的一项重要指标，测定水体中的氨氮有助于评价水体被污染情况和自净能力[1]。目前常用的氨氮在线检测方法主要有纳氏试剂分光光度法、水杨酸分光光度法、荧光法、气相色谱吸收法和氨气敏电极法[2-4]，这些方法均需要对水样进行添加化学试剂、加热等预处理，这种做法不仅提高了野外在线监测系统的运行成本，产生的检测废液也会对环境造成二次污染。而铵离子选择性电极法则无需添加试剂对水样进行预处理，且具有响应速度快、无二次污染等优点，更适用于对水体中氨氮浓度进行在线绿色监测。

然而基于铵离子选择电极的氨氮传感器在野外自然条件下易受温度变化影响，存在监测精度低、稳定性差等缺点，Huang等[5]在4、12、20、28、36 ℃ 时对基于铵离子选择性电极的氨氮传感器进行了氨氮检测对比实验，发现温度对氨氮检测结果有显著影响。因此，要提高传感器在野外自然环境下监测精度和稳定性还需要进行温度补偿。

目前中外关于氨氮温度补偿的研究多是基于氨氮传感器本身物理化学性能推导温度与传感器响应关系方程，Wen等[6]基于能斯特理论与经验公式建立温度与氨氮传感器输出二者关系模型，实现氨氮传感器温度补偿。一些科研工作者，如文献[7-8]等基于能斯特方程，采用多元回归分析的方法，建立氨氮温度补偿模型。上述研究工作均是以传感器本身理化性质展开进行研究的，但受限于成品传感器材料性能均已固定，在野外复杂环境下很难做到与实验室环境相同的工作性能，而且通过多元回归拟合的多项式模型结构简单，很难准确描述氨氮传感器受温度干扰的非线性变化。随着人工智能算法研究的不断深入，数据驱动的机器学习算法开始应用到传感器的优化研究中，其中支持向量机作为机器学习中的经典算法，凭借对小样本、非线性问题良好的适用性和泛化性能好等诸多优势在传感器抗干扰领域展现出巨大的优势[9-10]。因此，现将支持向量(support vector regression，SVR)算法应用在氨氮传感器温度补偿研究中，并结合粒子群优化(particle swarm optimization，PSO)算法对支持向量机模型输入参数进行寻优，摒弃传统根据经验选取参数存在的主观性与任意性[11]提高模型的精度，以更好地描述温度与氨氮传感器之间的非线性关系，解决传统氨氮温度补偿方法的不足，提高氨氮在线监测系统监测的精度和稳定性。

1 实验部分

1.1 铵离子选择性电极结构及检测原理

(1)

铵离子选择性电极是一种电化学传感器，如图1所示，铵离子选择性电极由内参比电极、内充溶液、铵离子选择性膜、电极外壳组成。

图1 铵离子选择性电极的结构示意图

(2)

通过能斯特方程可以计算出溶液中氨离子浓度，进而通过游离氨和氨离子在水中存在的比例关系得到总的氨氮值。由式(2)可以看出温度的变化对基于铵离子选择性电极的氨氮传感器输出的电位产生影响。

1.2 实验准备

实验设备选用ANB-300氨氮变送器(精确度1%，分辨率0.1)、电子温度计(0～50 ℃，精度0.1)和79-1型恒温搅拌器，实验试剂为100 mg/L氨氮标准贮备液和去离子水。将100 mg/L氨氮标准试剂通过去离子水按比例稀释成1、5、10、15、20、25、30、35、40 mg/L的氨氮溶液以备后续实验使用。

实验前分别用去离子水、1、10、100 mg/L氨氮标准溶液对电极进行标定，单次检测结束后，用去离子水清洗电极头部。检测时，对样品进行搅拌可以加快待测离子扩散速度，提高传感器响应速率。实验证明，搅拌速度为320 r/min时实验效果最佳。

1.3 氨氮温度实验与结果分析

分别调节1、5、10、15、20、25、30、35、40 mg/L的氨氮标准溶液的检测温度，记录每组溶液在0、5、10、15、20、25、30 ℃下传感器的输出值，每个温度梯度提取6个数据，将其平均值记为该温度下传感器的输出值，实验结果如表1所示。

对表1中实验数据进行相关性分析，上述9组氨氮检测温度实验中氨氮检测值与温度的相关系数均大于0.95，表明氨氮传感器输出值与环境温度具有强相关性。将表1中的检测结果与实验室常温(20 ℃)下氨氮溶液的标准浓度对比，并进行误差分析，结果如图2所示。分析可得除20 ℃以外，其他温度下传感器输出结果的误差均大于10%，最大误差出现在0 ℃下检测10 mg/L氨氮标准溶液时达到了31%，这个结果已经远远超出《地表水自动监测技术规范》(HJ 915—2017)中电极法允许相对误差为±10%的范围。因此为提高氨氮在线监测系统的稳定性和监测精度，需要对氨氮传感器进行在线温度补偿。

表1 各种浓度氨氮标准溶液在不同温度下的传感器输出值

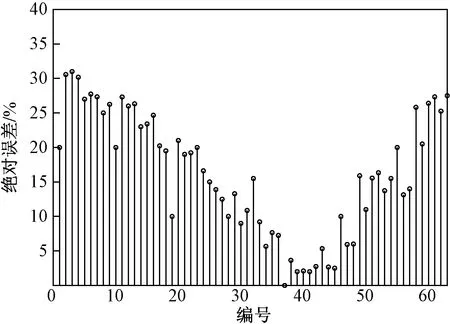
图2 氨氮传感器检测误差分析

2 PSO-SVR温度补偿模型

温度补偿可以将非标准温度的传感器输出换算成标准温度下的传感器输出，是建立在定标的基础上对数据进行修正。现有的温度补偿模型中，传统的多项式温度补偿模型结构简单，对温度干扰的非线性变化数据样本回归效果差。而SVR对非线性函数具有良好的拟合性能，模型补偿精度高，且基于结构风险最小化原则使其具有良好的泛化能力[12]。

参数优化是 SVR 建模中的一个重要问题，参数选择的不同会直接影响 SVM 模型的分类预测精度和泛化能力[13]。针对SVR在建立温度补偿模型时, 难以确定模型惩罚因子和核函数参数的问题, 提出了引入粒子群算法对模型参数进行寻优, 以提高模型的建模效率、预测准确度和泛化能力。

2.1 支持向量回归(SVR)原理

非线性SVR的基本思想是通过事先确定的非线性映射将输入向量映射的一个高维特征空间(Hilbert空间)中，然后在此高维空间中再进行线性回归，从而取得在原空间非线性回归的效果。

对于训练样本(xi,yi)(i=1,2,…,n)，xi∈Rn为输入量，yi∈R为输出量，其回归函数为

f(x)=ωφ(x)+b

(3)

式(3)中：φ(x)为非线性映射函数，可以将x输入向量映射到高维特征空间；ω为系数向量；b为阈值。

标准支持向量回归机采用ε-不敏感损失函数，且通过结构风险最小化原则得到SVR的目标函数和约束条件为

(4)

(5)

此时回归问题就转化为关于待求参数ω、b的凸二次规划问题，引入Lagrange函数得到式(4)、式(5)的对偶形式为

(6)

(7)

式中：φ(xi)·φ(xj)为高维空间的点积运算，令K(xi,xj)=φ(xi)·φ(xj)，称K(xi,xj)为核函数，通过引入核函数解决维数问题，可在不知映射函数的情况下实现回归估计。核函数的类型有多种，这里将RBF高斯径向基函数作为补偿模型的核函数。

将核函数代入式(6)求解，得到非线性拟合函数表达式为

(8)

式(8)中：K(x,xi)=exp(‖x-xi‖2/2σ2)。

2.2 粒子群优化算法(PSO)

粒子群优化(PSO)算法是计算智能领域除了蚁群算法和鱼群算法之外的一种群体智能的优化算法，该算法最早由Kennedy和Eberhart在1995年提出的，源自对鸟类捕食问题的研究[14]。PSO算法通过粒子搜寻自己找到的个体最优解和群体最优解完成优化。PSO算法基本流程如下。

(1)设置群体规模N，初始化粒子的位置xi和速度vi。

(2)计算每一个粒子的适应度值。

(3)计算每个粒子的适应度和个体极值Pi，比较两者大小，若适应度值大于Pi，则用适应度值赋予Pi。

(4)计算全局极值gi，将粒子的适应度值和全局极值gi比较，若适应度值大于gi则将适应度值赋予gi。

(5)更新粒子的位置xi和速度vi。

(6)当误差满足预期条件或达到最大循环次数时寻优结束，否则返回步骤(2)。

2.3 基于PSO-SVR算法的氨氮温度补偿模型

基于粒子群优化算法支持向量回归机的氨氮传感器温度补偿模型建模步骤如下。

(1)采集传感器检测水体氨氮时传感器输出与温度的变化数据如表1所示，建立训练样本集。

(2)选取核函数，选取RBF高斯径向基函数作为PSO-SVR模型的核函数。

(3)通过离子群优化算法优化SVR模型参数。根据每个粒子包含的参数训练SVR模型，将训练得到的补偿值与实际值对比计算均方根误差(root mean square error，RMSE)作为每个粒子的适应度，更新得到最优参数。

(4)将最佳的惩罚系数C和核函数参数g输入到SVR模型中，通过训练集训练的最终PSO-SVR氨氮传感器温度补偿模型。

通过MATLAB软件实现建模，设定粒子群初始参数为：最大迭代次数为200、粒子群规模为n=20、局部搜索能力c1=1.5、全局搜索能力c2=1.7，经过粒子群优化算法对SVR模型参数寻优，适应度如图3所示，经寻优后得到的模型最优参数惩罚系数C和核函数参数g分别为100、0.01。

图3 PSO算法参数寻优适应度变化曲线

3 模型验证与分析

3.1 PSO-SVR模型补偿效果评价

为了验证PSO-SVR算法建模的补偿效果，分别采用多元线性回归拟合三次曲面方程的温度补偿模型、传统的SVR模型和PSO-SVR模型在相同的训练集上进行训练，在同样的测试样本(表2)上比较模型的补偿精度。各模型的决定系数R2、均方根误差(RMSE)、测试集平均误差如表3所示，不同模型对训练样本的补偿效果及误差如图4所示。

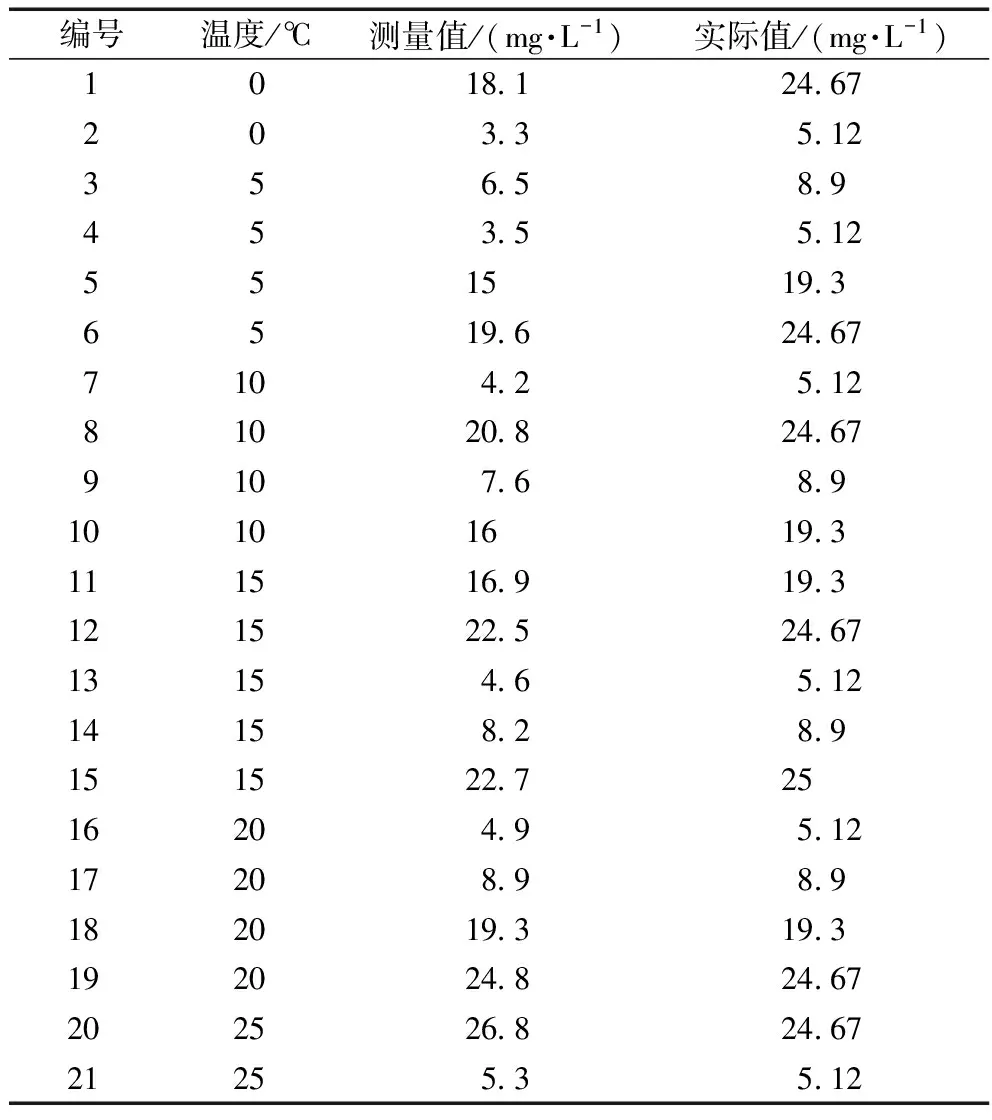
表2 测试集数据

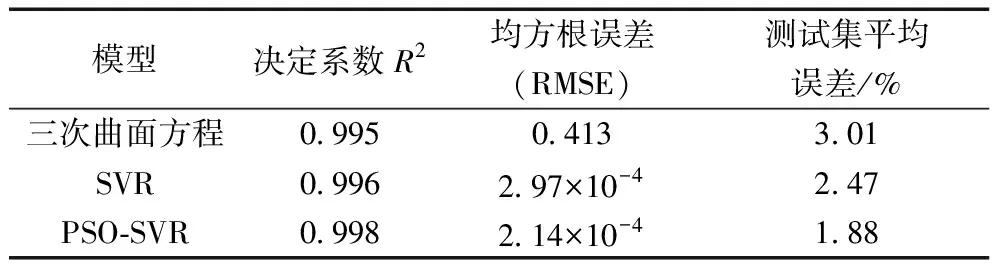
表3 3种模型补偿效果对比

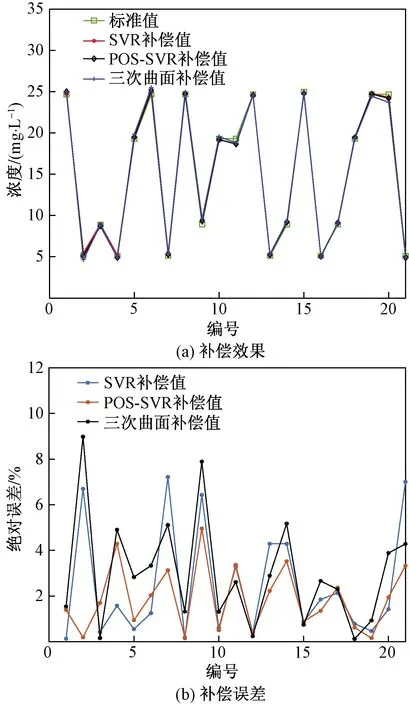
图4 不同模型补偿效果和补偿误差对比图

可以看出，最小二乘法拟合三次曲面方程的补偿准确度不高，表现较差，SVR和PSO-SVR模型都具有良好的非线性拟合性能，但PSO-SVR模型的决定系数较高，均方根误差(RMSE)和测试集平均误差较小，误差基本集中在4%以内，补偿精度要优于其他两个模型，补偿效果最为优异。

3.2 实际水样检测对比实验

在野外水域提取6组水样，在随机温度下，采用本研究建立的氨氮传感器温度补偿模型所优化后的传感器测量氨氮浓度数据，并与国标法检测的同组水样检测结果对比如表4所示，可以看出两种测量结果最高偏差4.76%，最小偏差0.64%，偏差均小于5%，多数偏差在2%附近。由此可知，温度补偿模型对非建模数据具有良好的泛化性能和较高的精度，该模型补偿后的铵离子选择性电极能够满足野外低温环境下，在线监测系统对氨氮的检测要求。

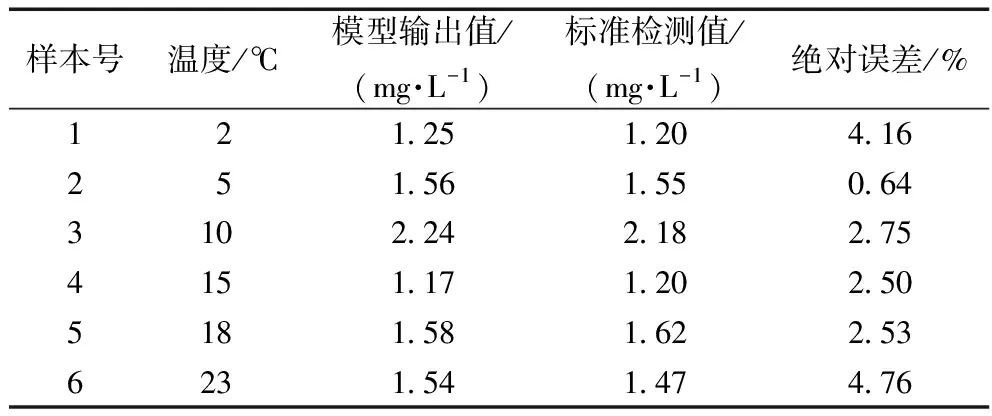
表4 实际水样补偿实验结果分析表

4 结论

基于粒子群优化支持向量回归算法(PSO-SVR)，针对铵离子选择性电极的氨氮传感器在实际使用过程中，氨氮检测结果容易受到环境温度变化的影响，造成检测结果失准的问题，建立氨氮温度补偿模型，以提高氨氮在线监测系统的检测精度和稳定性。

(1)将不同浓度的氨氮标准溶液，在不同温度下得到的传感器输出值与标准浓度进行对比，得出检测结果与标准溶液浓度存在偏差。在0 ℃下，检测10 mg/L氨氮标准溶液时最大偏差达到了31%，远超过技术规范的允许范围。

(2)建立PSO-SVR氨氮温度补偿模型。采用粒子群优化算法对SVR模型核心参数进行寻优，摒弃了通过经验等人为因素对核心参数的选取，使其相较于传统SVR和多元线性回归模型具有更好的模型精度。

(3)将野外实际水样实验中，模型补偿的结果与行业标准检测数据进行对比，误差均小于5%。由此可见，氨氮补偿模型能够有效地校正温度对氨氮检测结果的影响，对非建模数据也具有良好的泛化能力。研究可为野外低温环境下水体氨氮含量在线精准监测提供理论依据和参数支持。